2018届河北省武邑中学高三上学期期末考试数学(文)试题 Word版含答案

河北武邑中学高三年级上学期期末考试数学试题（文）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{}{}2|lgx 0,|4M x N N x =>=≤，则M N ⋂（ ） A ． []1,2 B ．()1,2 C ．[)1,2 D ．(]1,2 2.设复数满足243z i i -=+，则z =（ ）A ．44i +B ．44i -C ．22i -D ．22i +3.已知函数()log 2a y ax =-在[]0,1上是x 的函数，则a 的取值范围是（ ） A ．()0,1 B ．()1,2 C ．()0,2 D ．[)2,+∞4. 已知数列{}n a 满足：()111,212n n a a a n -==+≥，为求使不等式123n a a a a k ++++<的最大正整数n ，某人编写了如图所示的程序框图，在框图的判断框中的条件和输出的表达式分别为（ ） A ．,S k i < B ．,1S k i <- C. ,S k i ≥ D ．,1S k i ≥-5.设实数,x y 满足3010210x y y x x +-≤⎧⎪⎪-≥⎨⎪-≥⎪⎩，则y x u x y =-的取值范围为（ ）A ．1,22⎡⎤⎢⎥⎣⎦B ．2,23⎡⎤-⎢⎥⎣⎦ C. 23,32⎡⎤-⎢⎥⎣⎦ D ．33,22⎡⎤-⎢⎥⎣⎦6.有编号为1，2，…，700的产品，现需从中抽取所有编号能被7整除的产品为样品进行检验.下面是四位同学设计的程序框图，其中正确的是（ ）A ．B ．C. D ．7.某几何体的三视图如图所示，则该几何体的体积为（ ）A ．643π+．563π+18π D ．224π+ 8.如图，周长为1的圆的圆心C 在y 轴上，顶点()0,1A ，一动点M 从A 开始逆时针绕圆运动一周，记走过的弧长AB x =，直线AM 与x 轴交于点(),0N t ，则函数()t f x =的图像大致为（ ）A ．B ．C. D ．9.某工厂生产甲、乙两种产品，生产甲产品1件需消耗原料1千克，原料2千克；生产乙产品1件需消耗原料2千克，原料1千克；每件甲产品的利润是300元，每件乙产品的利润是400元，公司在生产这两种产品的计划中，要求每天消耗，原料都不超过12千克，通过合理安排计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（ ）A ． 1800元B ． 2400元 C. 2800元 D ．3100元 10.圆心在曲线()30y x x=>上，且与直线3430x y ++=相切的面积最小的圆的方程为（ ） A ． ()223292x y ⎛⎫-+-= ⎪⎝⎭ B ． ()()22216315x y ⎛⎫-+-= ⎪⎝⎭C. ()()22218135x y ⎛⎫-+-= ⎪⎝⎭D ．((229x y -+-=11.一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）A ．36πB ．1123π C. 32π D ．28π 12.若12,F F 为双曲线22221x y a b-=的左右焦点，O 为坐标原点，点P 在双曲线的左支上，点M 在双曲线的右准线上，且满足：()111,0OF OM FO PM OP OF OM λλ⎛⎫ ⎪==+> ⎪⎝⎭，则该双曲线的离心率为 （ ）A B C. 2 D ．3第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上13.平面向量a 与b 的夹角为60°，()2,0,1a b ==，则2a b += ． 14.已知某几何体的三视图如图所示，则这个几何体的体积为 ．15.甲、乙两艘轮船都要在某个泊位停靠4小时，假定它们在一昼夜的时间中随机地到达，则两艘船中至少有一艘在停靠泊位时必须等待的概率为 ．16. ABC ∆中，角,,A B C 所对的边分别为,,a b c ，向量()()2,1,2,cos q a p b c C ==-，且//p q ，三角函数式2cos 2C11tan Cμ-=++的取值范围是 ．三、解答题 ：共70分.解答应写出文字说明、证明过程或演算步骤. 第17-21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.17.已知数列{}n a ，{}n b 满足：()()111,1,411n n n n n n b a a b b a a -=+==-+． （1）设11n n C b =-，求数列{}n C 的通项公式； （2）设12231n n n S a a a a a a +=+++，不等式4n n aS b <恒成立时，求实数a 的取值范围．18.如图，在四棱锥P ABCD -中，底面ABCD 是边长为a 的正方形，E F 、分别为PC BD 、的中点，侧面PAD ⊥底面ABCD ，且2PA PD AD ==． （1）求证：//EF 平面PAD ； （2）求三棱锥C PBD -的体积．19.某企业为了对新研发的一批产品进行合理定价，将产品按事先拟定的价格进行试销，得到一组销售数据()(),1,2,6i i x y i =，如表所示：已知80y =， （1）求q 的值；（2）已知变量,x y 具有线性相关性，求产品销量y 关于试销单价x 的线性回归方程ˆˆˆybx a =+可供选择的数据662113050,271i ii i i x yx ====∑∑；（3）用ˆy表示（2）中所求的线性回归方程得到的与对应的i x 产品销量的估计值.当销售数据()(),1,2,6i i x y i =对应的残差的绝对值时，则将销售数据ˆ1i i yy -≤称为一个“好数据”.试求(),i i x y 这6组销售数据中的“好数据”.参数数据：线性回归方程中的ˆˆ,ba 最小二乘估计分别是()1221ˆˆˆ,ni ii nii x y nx yb ay bx xn x==-==--∑∑ 20.已知抛物线()2:20C y px p =>在第一象限内的点()2,t P 到焦点的距离为52． （1）若1,02M ⎛⎫-⎪⎝⎭，过点,M P 的直线1l 与抛物线相交于另一点Q ，求QF PF 的值； （2）若直线2l 与抛物线C 相交于,A B 两点，与圆()22:1M x a y -+=相交于,D E 两点，O 为坐标原点，OA OB ⊥，试问：是否存在实数a ，使得DE 的长为定值？若存在，求出的值；若不存在，请说明理由． 21. 已知函数()()2112x f x x e ax =--． （1）讨论()f x 的单调性；（2）若()f x 有两个零点，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为1cos sin x y αα=+⎧⎨=⎩（α为参数，0πα-<<），曲线2C 的参数方程为125x y ⎧=-⎪⎨⎪=+⎩（t 为参数），以O 为极点，x 轴的正半轴为极轴建立坐标系． （1）求曲线1C 的极坐标方程和曲线2C 的普通方程； （2）射线4πθ=-与曲线1C 的交点为P ，与曲线2C 的交点为Q ，求线段PQ 的长．23.选修4-5：不等式选讲已知函数()1f x x =+． （1）解不等式()21f x x ≥+；（2）x R ∃∈，使()()26f x f x m --+<成立，求m 的取值范围．试卷答案一、选择题1-5DCBBA 6-10 BBDCA 11、12：CC二、填空题13. 113616. (-三、解答题17.解：（1）∵11112n n b b --=--，∴12111111n n n n b b b b --==-+---， ∵11141c b ==--，∴数列{}n c 是以-4为首项，-1为公差的等差数列， ∴()()4113n c n n =-+--=--； （2）由（1）知，131n n c n b ==---，∴23n n b n +=+， 从而113n n a b n =-=+， ()()()12231111114556344444n n n n S a a a a a a n n n n +=+++=+++=-=⨯⨯++++， ∴()()()()21368244334n n n a n a n a n aS b n n n n -+-+-+-=-=++++， 由题意可知()()213680a n a n -+--<恒成立，即可满足不等式4n n aS b <恒成立，设()()()21368f n a n a n =-+--，当1a =时，()380f n n =--<恒成立，当1a >时，由()()213680a n a n -+--=的判别式()()2363210a a ∆=-+->，再结合二次函数的性质4n n aS b <不可能成立； 当1a <时，对称轴()323110,2121a n f n a a -⎛⎫=-=--< ⎪--⎝⎭在()1,+∞上为单调递减函数，∵()()()113684150f a a a =-+--=-<，∴1a <时，4n n aS b <恒成立， 综上知：当1a ≤时，4n n aS b <恒成立．18.解：（1）连结AC ，则F 是AC 的中点，E 为PC 的中点， 故在CPA ∆中，//EF PA ，且PA ⊂平面PAD ，EF ⊄平面PAD ， ∴//EF 平面PAD ；（2）取AD 的中点N ，连结PN ，∵PA PD =，∴PN AD ⊥， 又平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，∴PN ⊥平面ABCD ， ∴31111332212C PBD P BCD BCD a V V S PN a a a --∆====. 19.解：（1）∵84838075686q y +++++=，又∵80y =，∴8483807568806q +++++=，∴90q =；（2）4567891362x +++++==，∴21330506802ˆ41327162b-⨯⨯==-⎛⎫- ⎪⎝⎭， ∴()13ˆ8041062a=--⨯=， ∴ˆ4106yx =-+； （3）∵ˆ4106yx =-+， ∴1111ˆˆ410690,909001yx y y =-+=-=-=<，所以()()11,4,90x y =是好数据； 2222ˆˆ410686,868421yx y y =-+=-=-=>，所以()()22,5,84x y =不是好数据； 3333ˆˆ410682,838211yx y y =-+=-=-==，所以()()33,6,83x y =是好数据； 4444ˆˆ410678,788021yx y y =-+=-=-=>，所以()()44,7,80x y =不是好数据； 5555ˆˆ410674,757411yx y y =-+=-=-==，所以()()55,8,75x y =是好数据； 6666ˆˆ410670,706821yx y y =-+=-=-=>，所以()()66,9,68x y =不是好数据； 所以好数据为()()()4,90,6,68,8,75.20.解：（1）∵点()2,P t ，∴5222p +=，解得1p =， 故抛物线C 的方程为：22y x =，当2x =时，2t =， ∴1l 的方程为4255y x =+，联立可得212,8Q y x x ==， 又∵11,22Q P QF x PF x =+=+，∴111821422QF PF +==+；（2）设直线AB 的方程为x ty m =+，代入抛物线方程可得2220y ty m --=， 设()()1122,,A x y B x y ，则12122,2y y t y y m +==-，① 由OA OB ⊥得：()()12120ty m ty m y y +++=， 整理得()()22121210t y y tm y y m ++++=，② 将①代入②解得2m =，∴直线:2l x ty =+， ∵圆心到直线l的距离d =，∴DE =显然当2a =时，2,DE DE =的长为定值.21.解：（1）()()()1x x x f x e x e ax x e a '=+--=-， ①设0a ≤，则当(),0x ∈-∞时，()0f x '<；当()0,x ∈+∞时，()0f x '>，所以()f x 在(),0-∞单调递减，在()0,+∞单调递增； ②设0a >，由()0f x '=得0x =或ln x a =， 若1a =，则()()10x f x x e '=-≥， 所以()f x 在(),-∞+∞单调递增，若01a <<，则ln 0a <，故当()(),ln 0,x a ∈-∞+∞时，()0f x '>；当()ln ,0x a ∈时，()0f x '<，所以()f x 在()(),ln ,0,a -∞+∞单调递增，在()ln ,0a 单调递减； ③若1a >，则ln 0a >，故当()(),0ln ,x a ∈-∞+∞时，()0f x '>；当()0,ln x a ∈时，()0f x '<，所以()f x 在()(),0,ln ,a -∞+∞单调递增，在()0,ln a 单调递减；综上所述，当0a ≤时，()f x 在(),0-∞单调递减，在()0,+∞单调递增；当01a <<时()f x 在()(),ln ,0,a -∞+∞单调递增，在()0,ln a 单调递减；（2）①设0a ≤，则由（1）知，()f x 在(),0-∞单调递减，在()0,+∞单调递增，又()()01,1f f a =-=-，取b 满足3b <-且()ln b a =-，则()()()221220f b a b ab a b b >---=-+->，所以()f x 有两个零点；②设1a =，则()()1x f x x e =-，所以()f x 只有一个零点；③设01a <<，则由（1）知，()f x 在()(),ln ,0,a -∞+∞单调递增，在()ln ,0a 单调递减，()01f =-，当ln b a =时，()f x 有极大值()()()221220f b a b ab a b b =--=--+<，故()f x 不存在两个零点；当1a >时，则由（1）知，()f x 在()(),0,ln ,a -∞+∞单调递增，在()0,ln a 单调递减，当0x =时，()f x 有极大值()010f =-<，故()f x 不存在两个零点， 综上，a 的取值范围为0a ≤. 22.解：（1）曲线1C 的参数方程为1cos sin x y αα=+⎧⎨=⎩（α为参数，0πα-<<），普通方程为()()22110x y y -+=<，极坐标方程为2cos ,,02πρθθ⎛⎫=∈- ⎪⎝⎭，曲线2C的参数方程为1225x t y ⎧=-⎪⎨⎪=+⎩（t 为参数）， 普通方程260x y +-=； （2）,4πθρ=-=4P π⎫-⎪⎭；4πθ=-代入曲线2C的极坐标方程，可得ρ'=4Q π⎛⎫-⎪⎝⎭，∴PQ ==．23.解：（1）当10x +≥即1x ≥-时，121x x +≥+，∴10x -≤≤， 当10x +<即1x <-时，121x x --≥+，∴1x <-， ∴不等式的解集为{}|0x x ≤；（2）∵()()21,67f x x f x x -=-+=+，∴17x x m --+<，∵x R ∃∈，使不等式17x x m --+<成立，∴m 大于17x x --+的最小值， ∴8m >-.。

河北武邑中学2017—2018学年高三年级上学期期末考试数学试题（理）第Ⅰ卷（选择题共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设i 是虚数单位，复数1a i i为纯虚数，则实数a 的值为（）A ． 1B ． -1 C．12D ．-22.设为锐角，sin ,1,1,2a b，若a 与b 共线，则角（）A ． 15° B． 30° C．45° D．60°3.下列说法正确的是（）A ．命题“若2340x x ，则4x ”的否命题是“若2340xx ，则4x ”B ．0a 是函数ayx 在定义域上单调递增的充分不必要条件C ．,0,34x x x D ．若命题:,3500nP nN ，则:,3500n P x N 4. 已知点1,1,1,2,2,1,3,4A B CD ，则向量AB 在CD 方向上的投影为（）A ．322B ．3152 C.322D ．31525. 若双曲线222210,0x y ab ab的渐近线与直线1y所围成的三角形面积为2，则该双曲线的离心率为（）A ．52B ．2 C.3 D．56.《九章算术》卷五商功中有如下问题：今有刍甍（底面为矩形的屋脊的几何体），下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何，下图网格纸中实线部分分为此刍甍的三视图，设网格纸上每个小正方形的边长为1丈，那么此刍甍的体积为（）A．3立方丈 B．5立方丈 C.6立方丈 D．12立方丈7. 从1，2，3，…，9这个9个数中任取5个不同的数，则这5个数的中位数是5的概率等于（）A．57B．59C.27D．498. 将曲线1:sin6C y x上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移2个单位长度，得到曲线2:C y g x，则g x在,0上的单调递增区间是（）A．5,66B．2,36C.2,03D．,69.秦九韶是我国南宋时期的数学家，在他所著的《数书九章》中提出的多项式求值的“秦九韶算法”，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入,n x的值分别为4，2，则输出v的值为（）A． 32 B． 64 C. 65 D．13010. 若50,2a x yax y 展开式中42x y 的系数为-20，则a 等于（）A ． -1B ．32C. -2 D ．5211. 已知三棱锥P ABC 的所有顶点都在球O 的球面上，,,60,2,2,3PA AB PAAC BACPAABAC，则球O 的表面积为（）A ．403 B．303C.203D．10312.已知函数213ln 2fxxxax 在区间1,3上有最大值，则实数a 的取值范围是（）A ．1,52B．111,22 C. 111,22D ．1,52第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上13.已知抛物线220ypx p 的准线与圆22316x y相切，则p 的值为．14.已知实数,x y 满足2041xy xy y，则2y x的最小值为．15.已知,f x g x 分别是定义在R 上的偶函数和奇函数，且21xf xg xex，则函数h xf xg x 在点0,0h 处的切线方程是．16.已知a b c 、、是ABC 的三边，4,4,6,sin 2sin abA C ，则c 的取值范围为．三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.已知正项数列na 满足221111,nn nn a a a a a ，数列n b 的前n 项和n S 满足2nn S na ．（1）求数列n a ，n b 的通项公式；。

2018-2019学年河北省衡水市武邑中学高三（上）期末数学试卷（文科）一、选择题（本大题共12小题，每小题5分，共60分）1．（5分）已知集合M＝{x|（x﹣1）2＜4，x∈R}，N＝{﹣1，0，1，2，3}，则M∩N＝（）A．{0，1，2}B．{﹣1，0，1，2}C．{﹣1，0，2，3}D．{0，1，2，3} 2．（5分）设（i为虚数单位），则＝（）A．B．C．D．23．（5分）已知命题p：∀x∈N*，（）x≥（）x，命题q：∃x∈N*，2x+21﹣x＝2，则下列命题中为真命题的是（）A．p∧q B．（￢p）∧q C．p∧（￢q）D．（￢p）∧（￢q）4．（5分）若x，y满足则x+2y的最小值为（）A．0B．4C．5D．105．（5分）执行如图所示的程序框图，输入n＝5，m＝3，那么输出的p值为（）A．360B．60C．36D．126．（5分）在△ABC中，D为BC的中点，AB＝2，AC＝，则＝（）A．B．﹣C．3D．﹣37．（5分）函数f（x）＝sin（ωx+φ）（其中|φ|＜）的图象如图所示，为了得到y＝sinωx 的图象，只需把y＝f（x）的图象上所有点（）A．向右平移个单位长度B．向右平移个单位长度C．向左平移个单位长度D．向左平移个单位长度8．（5分）已知某几何体的正（主）视图，侧（左）视图和俯视图均为斜边长为的等腰直角三角形（如图），若该几何体的顶点都在同一球面上，则此球的表面积为（）A．4πB．3πC．2πD．π9．（5分）设F为抛物线C：y2＝4x的焦点，曲线y＝（k＞0）与C交于点P，PF⊥x轴，则k＝（）A．B．1C．D．210．（5分）设函数f（x）＝若f（m）＞f（﹣m），则实数m的取值范围是（）A．（﹣1，0）∪（0，1）B．（﹣∞，﹣1）∪（0，1）C．（﹣1，0）∪（1，+∞）D．（﹣∞，﹣1）∪（1，+∞）11．（5分）在三棱锥P﹣ABC中，P A⊥平面ABC，∠BAC＝120°，AP＝，M 是线段BC上一动点，线段PM长度最小值为，则三棱锥P﹣ABC的外接球的表面积是（）A．B．9C．18πD．40π12．（5分）函数f（x）是定义在（0，+∞）上的可导函数，f'（x）为其导函数，若x•f'（x）+f（x）＝e x（x﹣1），且f（2）＝0，则不等式f（x）＜0的解集为（）A．（0，1）B．（0，2）C．（1，2）D．（2，+∞）二、填空题（本大题共4小题，每小题5分，共20分）13．（5分）函数y＝log a（x﹣3）+3（a＞0且a≠1）恒过定点．14．（5分）已知函数f（x）的定义域为A，若其值域也为A，则称区间A为f（x）的保值区间．若g（x）＝x+m+lnx的保值区间是[e，+∞），则m的值为．15．（5分）已知三棱锥P﹣ABC的三条侧棱P A、PB、PC两两互相垂直，且P A＝PB＝PC ＝a，则该三棱锥的外接球的体积为．16．（5分）如图，在正方体ABCD﹣A1B1C1D1中，M，N分别为棱C1D1，C1C的中点，则直线AM与BN所成角的余弦值为．三、解答题（本大题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．（10分）已知向量，，函数．（1）求函数f（x）的单调递增区间；（2）已知a，b，c分别为△ABC内角A，B，C的对边，其中A为锐角，，c＝1，且f（A）＝1，求△ABC的面积S．18．已知数列{a n}满足．（1）证明：数列{a n+1}是等比数列；（2）令b n＝n（a n+1），数列{b n}的前n项和为T n，求T n．19．为了解人们对“延迟退休年龄政策”的态度，某部门从年龄在15岁到65岁的人群中随机调查了100人，将这100人的年龄数据分成5组：[15，25），[25，35），[35，45），[45，55），[55，65]，整理得到如图所示的频率分布直方图． 在这100人中不支持“延迟退休”的人数与年龄的统计结果如下：（1）由频率分布直方图，估计这100人年龄的平均数；（2）由频率分布直方图，若在年龄为[25，35），[35，45），[45，55）的三组内用分层抽样的方法抽取12人做问卷调查，求年龄在[35，45）组内抽取的人数；（3）根据以上统计数据填写下面的2×2列联表，据此表，能否在犯错误的概率不超过5%的前提下，认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异？附：K 2＝，其中n ＝a +b +c +d ．参考数据：20．已知抛物线E ：x 2＝2py （p ＞0）上一点M 的纵坐标为6，且点M 到焦点F 的距离为7． （1）求抛物线E 的方程；（2）设l1，l2为过焦点F且互相垂直的两条直线，直线l1与抛物线E相交于A，B两点，直线l2与抛物线E相交于C，D两点，若直线l1的斜率为k（k≠0），且S△OAB•S△OCD＝8，试求k的值．21．（12分）已知椭圆C的中心在原点，焦点在x轴上，左右焦点分别为F1，F2，且|F1F2|＝2，点（1，）在椭圆C上．（1）求椭圆C的方程；（2）过F1的直线l与椭圆C相交于A，B两点，且△AF2B的面积为，求直线l的方程．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，曲线C1的参数方程为（α为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为．（1）求曲线C1，C2的直角坐标方程；（2）判断曲线C1，C2是否相交，若相交，请求出交点间的距离；若不相交，请说明理由．[选修4-5：不等式选讲]23．已知函数f（x）＝|x+2a|+|x﹣a|．（1）当a＝1时，求不等式f（x）≥4﹣|x+2|的解集；（2）设a＞0，b＞0，且f（x）的最小值为t．若t+3b＝3，求的最小值．2018-2019学年河北省衡水市武邑中学高三（上）期末数学试卷（文科）参考答案与试题解析一、选择题（本大题共12小题，每小题5分，共60分）1．【解答】解：由（x﹣1）2＜4，解得：﹣1＜x＜3，即M＝{x|﹣1＜x＜3}，∵N＝{﹣1，0，1，2，3}，∴M∩N＝{0，1，2}．故选：A．2．【解答】解：∵＝，∴|z|＝，∴＝．故选：B．3．【解答】解：命题p：∀x∈N*，（）x≥（）x，利用指数函数的性质可得：是真命题；命题q：由2x+21﹣x＝2，化为：（2x）2﹣2•2x+2＝0，解得2x＝，∴x＝，因此q 是假命题．则下列命题中为真命题的是P∧（￢q），故选：C．4．【解答】解：作出不等式组对应的平面区域，由z＝x+2y，得y＝﹣x+，平移直线y＝﹣x+，由图象可知当直线经过点A（2，1）时，直线y＝﹣x+的截距最小，此时z最小，此时z＝2+2×1＝4．故选：B．5．【解答】解：模拟执行程序框图，依次写出每次循环得到的p的值，可得程序框图实质是计算排列数的值，当n＝5，m＝3时，可得：＝60．故选：B．6．【解答】解：由三角形法则可得：＝（+），＝﹣，所以•＝（）•（﹣）＝（2﹣2）＝（7﹣4）＝故选：A．7．【解答】解：由题意可得×＝﹣＝，∴ω＝2．再由五点法作图可得2×+∅＝π，∴∅＝，故函数f（x）＝sin（ωx+ϕ）＝sin（2x+）＝sin2（x+）．故把y＝f（x）的图象向右平移个单位长度可得y＝sinωx的图象，故选：A．8．【解答】解：由已知可得，该几何体为三棱锥，其外接球等同于棱长为1的正方体的外接球，故球半径R满足2R＝，故球的表面积S＝4πR2＝3π，故选：B．9．【解答】解：抛物线C：y2＝4x的焦点F为（1，0），曲线y＝（k＞0）与C交于点P在第一象限，由PF⊥x轴得：P点横坐标为1，代入C得：P点纵坐标为2，故k＝2，故选：D．10．【解答】解：函数f（x）＝，当m＞0，f（m）＞f（﹣m）即为﹣lnm＞lnm，即lnm＜0，解得0＜m＜1；当m＜0，f（m）＞f（﹣m）即为ln（﹣m）＞﹣ln（﹣m），即ln（﹣m）＞0，解得m＜﹣1．综上可得，m＜﹣1或0＜m＜1．故选：B．11．【解答】解：如图所示：三棱锥P﹣ABC中，P A⊥平面ABC，AP＝，M是线段BC上一动点，线段PM长度最小值为，则：当AM⊥BC时，线段PM达到最小值，由于：P A⊥平面ABC，所以：P A2+AM2＝PM2，解得：AM＝1，所以：BM＝，则：∠BAM＝60°，由于：，∠BAC＝120°，所以：∠MAC＝60°则：△ABC为等腰三角形．所以：BC＝2，在△ABC中，设外接圆的直径为2r＝，则：r＝2，所以：外接球的半径R═，则：S＝，故选：C．12．【解答】解：函数f（x）是定义在（0，+∞）上的可导函数，f'（x）为其导函数，令φ（x）＝xf（x），则φ′（x）＝x•f'（x）+f（x）＝e x（x﹣1），可知当x∈（0，1）时，φ（x）是单调减函数，并且0•f'（0）+f（0）＝e0（0﹣1）＝﹣1＜0，即f（0）＜0x∈（1，+∞）时，函数是单调增函数，f（2）＝0，则φ（2）＝2f（2）＝0，则不等式f（x）＜0的解集就是xf（x）＜0的解集，不等式的解集为：{x|0＜x＜2}．故选：B．二、填空题（本大题共4小题，每小题5分，共20分）13．【解答】解：当x﹣3＝1，即x＝4时，y＝log a（x﹣3）+3＝0+3＝3，∴函数y＝2log a（x﹣3）+3的图象恒过定点（4，3）．故答案为：（4，3）．14．【解答】解：若g（x）＝x+m+lnx的保值区间是[e，+∞），则可得g（x）＝x+m+lnx定义域和值域都是[e，+∞）∵g（x）＝x+m+lnx在[e，+∞）上单调递增∴g（x）min＝g（e）＝e+m+lne＝e∴m＝﹣1故答案为：﹣115．【解答】解：由P A、PB、PC两两互相垂直，且P A＝PB＝PC＝a，可知该三棱锥为正方体的一角，其外接球直径为体对角线长，即2R＝，∴，∴V＝＝＝π．故答案为：π．16．【解答】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，设正方体ABCD﹣A1B1C1D1中棱长为2，则A（2，0，0），M（0，1，2），B（2，2，0），N（0，2，1），＝（﹣2，1，2），＝（﹣2，0，1），设直线AM与BN所成角为θ，cosθ＝＝＝．∴直线AM与BN所成角的余弦值为．故答案为：．三、解答题（本大题共5小题，共70分．解答应写出文字说明，证明过程或演算步骤．）17．【解答】解：（1）＝＝＝＝＝sin（2x﹣），由（k∈z），函数f（x）的单调递增区间为（k∈z）．（2），因为，，所以.，，又a2＝b2+c2﹣2bc cos A，则b＝2，从而．18．【解答】解：（1）证明：数列{a n}满足，可得a1＝S1＝2a1﹣1，解得a1＝1；n≥2时，a n＝S n﹣S n﹣1＝2a n﹣n﹣（2a n﹣1﹣n+1）＝2a n﹣2a n﹣1﹣1，化为a n＝2a n﹣1+1，可得a n+1＝2（a n﹣1+1），则数列{a n+1}是首项、公比均为2的等比数列；（2）b n＝n（a n+1）＝n•2n，前n项和为T n＝1•2+2•22+…+n•2n，2T n＝1•22+2•23+…+n•2n+1，两式相减可得﹣T n＝2+22+…+2n﹣n•2n+1＝﹣n•2n+1，化简可得T n＝2+（n﹣1）•2n+1．19．【解答】解：（1）由频率分布直方图，估计这100人年龄的平均数为＝20×0.2+30×0.1+40×0.2+50×0.3+60×0.2＝42（岁）；（2）由频率分布直方图知，在年龄为[25，35），[35，45），[45，55）的三组内，用分层抽样的方法抽取12人，则在[35，45）组内抽取的人数为12×＝4（人）；（3）由题意填写列联表如下，计算观测值K2＝＝6.25＞3.841，能在犯错误的概率不超过5%的前提下，认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异．20．【解答】解：（1）抛物线E：x2＝2py的准线方程为y＝﹣，由题意可得|MF|＝6+＝7，解得p＝2，即x2＝4y；（2）设l1：y＝kx+，即y＝kx+1，联立x2＝4y，可得x2﹣4kx﹣4＝0，即有x1+x2＝4k，x1x2＝4，则|AB|＝•＝•＝4（1+k2），且O到直线l1的距离为，则S△OAB＝••4（1+k2）＝2，由于直线l2与l1垂直，且都过F，可得S△OCD＝2，由S△OAB•S△OCD＝8，可得•＝2，即k4﹣2k2+1＝0，解得k＝±1．21．【解答】解：（1）由题意可设椭圆C的方程为（a＞b＞0），由|F1F2|＝2得c＝1，∴F1（﹣1，0），F2（1，0），又点（1，）在椭圆C上，∴，a＝2．则b2＝a2﹣c2＝4﹣1＝3．∴椭圆C的方程为；（2）如图，设直线l的方程为x＝ty﹣1，A（x1，y1），B（x2，y2），把x＝ty﹣1代入，得：（3t2+4）y2﹣6ty﹣9＝0∴，∴＝＝，∴，∴t2＝1，解得：（舍）或t2＝1，t＝±1．故所求直线方程为：x±y+1＝0．[选修4-4：坐标系与参数方程]22．【解答】解：（1）将，消去参数，得曲线C1的直角坐标方程为，将展开整理，得，因为x＝ρcosθ，y＝ρsinθ，所以曲线C2的直角坐标方程为．（2）由（1）知曲线C2是过定点的直线，因为点在曲线C1的内部，所以曲线C1与曲线C2相交．将代入并整理，得7y2+6y﹣1＝0，设曲线C1，C2的两交点为A（x1，y1），B（x2，y2），则，，故曲线C1，C2两交点间的距离．[选修4-5：不等式选讲]23．【解答】解：（1）当a＝1时，f（x）＝|x+2|+|x﹣1|，原不等式可化为2|x+2|+|x﹣1|≥4，①当x≤﹣2时，不等式①可化为﹣2x﹣4﹣x+1≥4，解得，此时；当﹣2＜x＜1时，不等式①可化为2x+4﹣x+1≥4，解得x≥﹣1，此时﹣1≤x＜1；当x≥1时，不等式①可化为2x+4+x﹣1≥4，解得，此时x≥1，综上，原不等式的解集为．（2）由题意得，f（x）＝|x+2a|+|x﹣a|≥|（x+2a）﹣（x﹣a）|＝3a，因为f（x）的最小值为t，所以t＝3a，由3a+3b＝3，得a+b＝1，所以＝，当且仅当，即，时，的最小值为．。

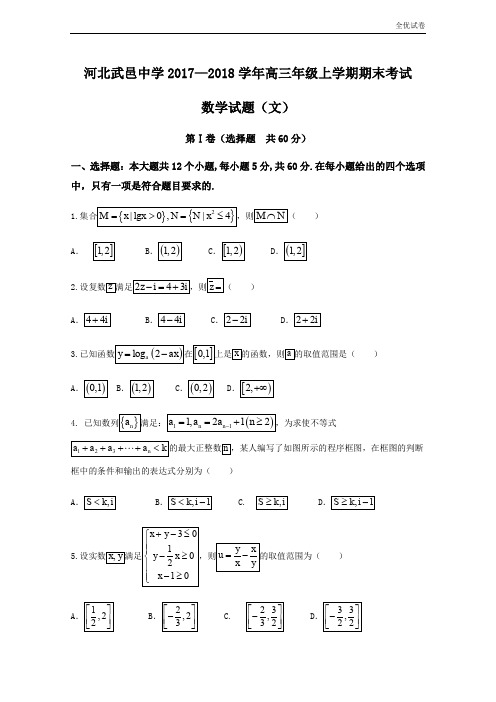
河北武邑中学2017—2018学年高三年级上学期期末考试数学试题（文）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.）A ．2.）A3.） A4.框中的条件和输出的表达式分别为（ ）A5.）A6.有编号为1，2，…，700的产品，现需从中抽取所有编号能被7整除的产品为样品进行检验.下面是四位同学设计的程序框图，其中正确的是（）A7.某几何体的三视图如图所示，则该几何体的体积为（）A8.如图，周长为1像大致为（）A9.某工厂生产甲、乙两种产品，生产甲产品1件需消耗原料1千克，原料2千克；生产乙产品1件需消耗原料2千克，原料1千克；每件甲产品的利润是300元，每件乙产品的利润是400元，公司在生产这两种产品的计划中，要求每天消耗，原料都不超过12千克，通过合理安排计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（）A． 1800元 B． 2400元 C. 2800元 D．3100元10.（）A．．11.一个几何体的三视图如图所示，该几何体外接球的表面积为（）A12.1OF OM ⎪+⎪线的离心率为（）A．3第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上13.60,b =b 14.已知某几何体的三视图如图所示，则这个几何体的体积为．15.甲、乙两艘轮船都要在某个泊位停靠4小时，假定它们在一昼夜的时间中随机地到达，则两艘船中至少有一艘在停靠泊位时必须等待的概率为 ．且的取值范围是 ．三、解答题 ：共70分.解答应写出文字说明、证明过程或演算步骤. 第17-21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.17.（1（218.（1（219.某企业为了对新研发的一批产品进行合理定价，将产品按事先拟定的价格进行试销，得到（1（2（32.当销售数“好数据”.6组销售数据中的“好数据”.20.（1（2的值；若不存在，请说明理由．21.（1（2请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程，曲，系．（1（223.选修4-5：不等式选讲（1（2试卷答案一、选择题1-5:DCBBA 6-10: BBDCA 11、12：CC二、填空题三、解答题17.解：（1-4为首项，-1为公差的等差数列， )()1n -=-（2）由（111n c b =-()()455634n n =+++⨯⨯++1a =--8415a -=-18.解：（1（232212a a ==. 19.解：（1（2（320.解：（1（2.21.解：（1(ln,a+∞)+∞单调递增，在综上所述，（211则由（1）点，22.解：（1，，（223.解：（1（2。

河北武邑中学2017-2018学年高三年级上学期第二次调研考试数学试题（文科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集R U =，集合{}02A x x =<≤，{}1B x x =<，则集合A B =U （ ） A ．()2,+∞ B ．[)2,+∞ C ．(],2-∞ D ．(],1-∞2．已知向量()2,1a =-r ，()1,3b =-r，则（ ）A ．a b ∥r rB ．a b ⊥r rC ．()a a b -∥r r rD ．()a ab ⊥-r r r3．以角θ的顶点为坐标原点，始边为x 轴的非负半轴，建立平面直角坐标系，角θ终边过点()2,4P ，则tan 4⎛⎫+= ⎪⎝⎭πθ（ ） A ．3- B ．13-C ．13D ．3 4．若函数()2log 129xf x x +=+-，则()3f =（ ） A ．7 B ．10 C ．11 D ．205．已知01a b c <<<<，log a m c =，log b n c =，cr a =，则m n r ，，的大小关系是（ ）A ．n m r <<B ．m r n <<C ．r m n <<D ．m n r << 6．如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点.若BE BA BD =+λμu u r u u r u u u r（R ∈λμ，），则+=λμ（ ）A ．1B ．34 C ．23 D ．127）①tan 25tan3525tan35︒+︒︒；②()2sin35cos25cos35cos65︒︒+︒︒；③1tan151tan15+︒-︒；④2tan61tan6-ππ.A ．①②B ．③C ．①②③D ．②③④8．已知函数()()cos 1f x A x =++ωϕ（0A >，0>ω，0<<ωπ）的最大值为3，()y f x =的图象的相邻两条对称轴间的距离为2，与y 轴的交点的纵坐标为1，则13f ⎛⎫= ⎪⎝⎭（ ）A ．1B ．1- C．0 9．cos y x x =+的大致图象是（ ）A ．B ．C ．D ．10．一艘海轮从A 处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，30分钟后到达B 处，在C 处有一座灯塔，海轮在A 处观察灯塔，其方向是南偏东70°，在B 处观察灯塔，其方向是北偏东65°，那么B C ，两点间的距离是（ ） A．海里 B． C． D．海里 11．已知函数()1ln sin 2f x x x a x ⎛⎫=++- ⎪⎝⎭π在区间,3⎛⎫⎪⎝⎭ππ上有最大值，则实数a 的取值范围是（ ）A ．14,2⎛⎫- ⎪⎝⎭ B ．34,2⎛⎫--⎪⎝⎭ C ．13,2⎛⎫- ⎪⎝⎭ D ．33,2⎛⎫-- ⎪⎝⎭12．已知定义在R 上的奇函数()f x 满足()()f x f x +=-π，当0,2x ⎡⎤∈⎢⎥⎣⎦π时，()f x =则函数()()()1g x x f x =--π在区间3,32⎡⎤-⎢⎥⎣⎦ππ上所有零点之和为（ ） A ．π B ．2π C ．3π D ．4π第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13．已知函数()3sin,03log ,0xx f x x x ⎧≤⎪=⎨⎪>⎩π，则13f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦． 14．若函数()y f x =的图象在4x =处的切线方程是29y x =-+，则()()44f f '-= ．15．函数()()sin f x A x =+ωϕ（00A >>ω，，2≤πϕ）的部分图象如图所示，其单调递减区间为2,63k k ⎡⎤++⎢⎥⎣⎦ππππ（k Z ∈），则2f ⎛⎫= ⎪⎝⎭π ．16．在ABC ∆中，a b c 、、分别为角A B C 、、的对边，已知2b ac =，22a c ac bc -=-，则sin cb B= ．三、解答题 （本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．已知函数()2sin 22sin sin x x f x x-=.（1）求()f x 的定义域及最小正周期； （2）求()f x 在[]0,π上的单调递增区间.18．已知函数()cos 4f x ax x b =-+π的图象在点,22f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭ππ处的切线方程为324y x =+π. （1）求a b ，的值； （2）求函数()f x 在,22⎡⎤-⎢⎥⎣⎦ππ上的最大值. 19．已知函数()32264a a f x x x ax =---的图象过点104,3A ⎛⎫ ⎪⎝⎭. （1）求函数()f x 的单调增区间；（2）若函数()()23g x f x m =-+有3个零点，求m 的取值范围.20．在ABC ∆中，内角,,A B C 所对的边分别为,,a b c .已知2cos 3A =，sinBC =. （1）求tan C 的值；（2）若a =ABC ∆的面积.21．如图所示，某小区为美化环境，准备在小区内草坪的一侧修建一条直路OC ，另一侧修建一条休闲大道，它的前一段OD 是函数y =()0k >的一部分，后一段DBC 是函数()sin y A x =+Φω（00A >>ω，，2Φ<π），[]4,8x ∈时的图象，图象的最高点为B ⎛ ⎝，DF OC ⊥，垂足为F . （1）求函数()sin y A x =+Φω的解析式；（2）若在草坪内修建如图所示的儿童游乐园PMFE ，问点P 落在曲线OD 上何处时，儿童乐园的面积最大？22．已知函数()()211ln 12f x x a x a x =-+++.（1）若2x =是()f x 的极值点，求()f x 的极大值； （2）求实数a 的范围，使得()1f x ≥恒成立.河北武邑中学2017-2018学年高三年级上学期第二次调研考试数学试题（文科）答案一、选择题1-5:CDACA 6-10:BCDBA 11、12：CD二、填空题13．．1- 15．32- 16三、解答题17．解：（1）由sin 0x ≠，得()x k k ≠∈Z π. 所以()f x 的定义域为{},x x k k ∈≠∈R Z π.因为()2sin 22sin sin x xf x x-=，2cos 2sin 4x x x ⎛⎫=-=+ ⎪⎝⎭π，∴()f x 的最小正周期为π.（2）函数cos y x =的单调递增区间为[]()2,22k k k ++∈Z ππππ 由2224k x k +≤+≤+πππππ，()x k k ≠∈Z π，且()0,x ∈π，所以()f x 在()0,π上的单调递增区间为3,4⎡⎫⎪⎢⎣⎭ππ. 18．解：（1）因为()cos 4f x ax x b =-+π，所以()sin f x a x '=+.又3122f a ⎛⎫'=+=⎪⎝⎭π，3224224f a b ⎛⎫=+=⨯+ ⎪⎝⎭πππππ，解得12a =，3b =.（2）由（1）知()13cos 24f x x x =-+π. 因为()1sin 2f x x '=+，由()1sin 02f x x '=+>，得62x -<<ππ，由()1sin 02f x x '=+<得，26x -<<-ππ，所以函数()f x 在,26⎡⎫--⎪⎢⎣⎭ππ上递减，在,62⎛⎤- ⎥⎝⎦ππ上递增. 因为22f ⎛⎫-= ⎪⎝⎭ππ，2f ⎛⎫= ⎪⎝⎭ππ，所以()max2f x f ⎛⎫== ⎪⎝⎭ππ. 19．解：（1）因为函数()32264a a f x x x ax =---的图象过点104,3A ⎛⎫⎪⎝⎭. 所以321044233a a a ---=，解得2a =， 即()32112232f x x x x =---，所以()22f x x x '=--.由()0f x '>，得1x <-或2x >.所以函数()f x 的递增区间是(),1-∞-，()2,+∞. （2）由（1）知()()max 11132f x f =-=--5226+-=-， 同理，()()min8223f x f ==-16423--=-，由数形结合思想，要使函数()()23g x f x m =-+有三个零点， 则1652336m -<-<-，解得713612m -<<. 所以m 的取值范围为713,612⎛⎫- ⎪⎝⎭. 20．解：（1）∵2cos 03A =>，∴sin A ==，()sin sin C B A C ==+sin cos sin cos A C C A =+2sin 33C C =+.整理得tan C =.（2）由tan C =得sin C =. 又由正弦定理知：sin sin a cA C=，故c =（1）对角A 运用余弦定理：2222cos 23b c a A bc +-==.（2）解（1）（2）得：b =3b =（舍去）.∴ABC ∆的面积为：S =21．解：又2<πϕ，所以3=-πϕ，故363y ⎛⎫=- ⎪⎝⎭ππϕ（2）在63y ⎛⎫=- ⎪⎝⎭ππϕ中令4x =，得()4,4D从而曲路OD 的方程为)04y x =≤≤设点2,4t P t ⎛⎫ ⎪⎝⎭，则矩形的面积()244t S t t ⎛⎫=- ⎪⎝⎭()04t ≤≤，()()234044t S t t '=-≤≤，t ⎛∈ ⎝⎭时，()0S t '>，()S t 递增，4t ⎫∈⎪⎪⎝⎭时，()0S t '<，()S t 递减，所以3t =时矩形的面积最大，P 点的坐标为43⎛ ⎝⎭. 22．解：（1）()()1af x x a x'=-++ ∵2x =是()f x 的极值点 ∴()()22102af a '=-++=解得2a = 当2a =时，()23f x x x '=-+=()()21232x x x x x x---+= 当x 变化时，()f x 的极大值为()312f =-.（2）要使得()1f x ≥恒成立，即0x >时，()211ln 02x a x a x -++≥恒成立， 设()()211ln 2g x x a x a x =-++， 则()()1a g x x a x '=-++()()1x x a x--=. （i ）当0a ≤时，由()0g x '<得函数()g x 单调减区间为()0,1，由()0g x '>得函数()g x 单调增区间为()1,+∞，此时()()min 1102g x g a ==--≥，得12a ≤-. （ii ）当01a <<时，由()0g x '<得函数()g x 单调减区间为(),1a ，由()0g x '>得函数()g x 单调增区间为()0,a ，()1,+∞，此时()1102g a =--<，∴不合题意. （iii ）当1a =时，()()210x g x x-'=≥，()g x 在()0,+∞上单调递增，此时()1102g a =--<，∴不合题意. （iv ）当1a >时，由()0g x '<得函数()g x 单调减区间为()1,a ，由()0g x '>得函数()g x 单调增区间为()0,1，(),a +∞，此时()1102g a =--<，∴不合题意.综上所述：12a ≤-时，()1f x ≥恒成立.。

河北武邑中学2017—2018学年高三年级上学期期末考试数学试题（理）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.设i 是虚数单位，复数1a ii-+为纯虚数，则实数a 的值为（ ） A ． 1 B ． -1 C ．12D ．-2 2.设α为锐角，()()sin ,1,1,2a b α==，若a 与b 共线，则角α=（ ） A ． 15° B ． 30° C ．45° D ．60° 3.下列说法正确的是（ ）A ．命题“若2340x x --=，则4x =”的否命题是“若2340x x --=，则4x ≠ ”B ．0a >是函数a y x =在定义域上单调递增的充分不必要条件C ．()000,0,34x x x ∃∈-∞<D ．若命题:,3500n P n N ∀∈>，则00:,3500n P x N ⌝∃∈≤4. 已知点()()()()1,1,1,2,2,1,3,4A B C D ---，则向量AB 在CD 方向上的投影为（ ）A ．2 B C. 2- D ． 5. 若双曲线()222210,0x y a b a b-=>>的渐近线与直线1y =-所围成的三角形面积为2，则该双曲线的离心率为（ ）A ．2B D 6.《九章算术》卷五商功中有如下问题：今有刍甍（底面为矩形的屋脊的几何体），下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何，下图网格纸中实线部分分为此刍甍的三视图，设网格纸上每个小正方形的边长为1丈，那么此刍甍的体积为（ ）A ．3立方丈B ．5立方丈 C.6立方丈 D ．12立方丈7. 从1，2，3，…，9这个9个数中任取5个不同的数，则这5个数的中位数是5的概率等于（ ） A ．57 B ．59 C. 27 D ．498. 将曲线1:sin 6C y x π⎛⎫=- ⎪⎝⎭上各点的横坐标缩短到原的12倍，纵坐标不变，再把得到的曲线向左平移2π个单位长度，得到曲线()2:C y g x =，则()g x 在[],0π-上的单调递增区间是（ ） A ．5,66ππ⎡⎤--⎢⎥⎣⎦ B ．2,36ππ⎡⎤--⎢⎥⎣⎦ C. 2,03π⎡⎤-⎢⎥⎣⎦D ．,6ππ⎡⎤--⎢⎥⎣⎦ 9.秦九韶是我国南宋时期的数学家，在他所著的《数书九章》中提出的多项式求值的“秦九韶算法”，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入,n x 的值分别为4，2，则输出v 的值为（ ）A ． 32B ． 64 C. 65 D ．13010. 若()()50,2a x y ax y <-+展开式中42x y 的系数为-20，则a 等于（ ）A ． -1B ． 32- C. -2 D ．52-11. 已知三棱锥P ABC -的所有顶点都在球O 的球面上，0,,60,2,2,3PA AB PA AC BAC PA AB AC ⊥⊥∠====，则球O 的表面积为（ ）A ．403π B ．303π C. 203π D ．103π 12.已知函数()213ln 2f x x x a x ⎛⎫=-+- ⎪⎝⎭在区间()1,3上有最大值，则实数a 的取值范围是（ ）A ．1,52⎛⎫- ⎪⎝⎭B ．111,22⎛⎫- ⎪⎝⎭ C. 111,22⎛⎫ ⎪⎝⎭ D ．1,52⎛⎫⎪⎝⎭第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上13.已知抛物线()220y px p =>的准线与圆()22316x y -+=相切，则p 的值为 ．14.已知实数,x y 满足2041x y x y y -≥⎧⎪+≤⎨⎪≥⎩，则2y x +的最小值为 ．15.已知()(),f x g x 分别是定义在R 上的偶函数和奇函数，且()()21x f x g x e x -=++，则函数()()()h x f x g x =+在点()()0,0h 处的切线方程是 ．16.已知a b c 、、是ABC ∆的三边，()4,4,6,sin 2sin a b A C =∈=，则c 的取值范围为 ． 三、解答题 ：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.已知正项数列{}n a 满足221111,n n n n a a a a a ++=+=-，数列{}n b 的前n 项和n S 满足2n n S n a =+．（1）求数列{}n a ，{}n b 的通项公式；（2）求数列11n n a b +⎧⎫⎨⎬⎩⎭的前n 项和n T ．18.已知表1和表2是某年部分日期的天安门广场升旗时刻表： 表1：某年部分日期的天安门广场升旗时刻表表2：某年1月部分日期的天安门广场升旗时刻表（1）从表1的日期中随机选出一天，试估计这一天的升旗时刻早于7：00的概率； （2）甲、乙二人各自从表2的日期中随机选择一天观看升旗，且两人的选择相互独立，记X 为这两人中观看升旗的时刻早于7：00的人数，求X 的 分布列和数学期望； （3）将表1和表2的升旗时刻化为分数后作为样本数据（如7：31化为31760），记表2中所有升旗时刻对应数据的方差为2s ，表1和表2中所有升旗时刻对应数据的方差为20s ，判断2s 与20s 的大小（只需写出结论）．19.如图，直角梯形BDFE 中，//,,EF BD BE BD EF ⊥=ABCD 中，//,,24AB CD AC BD AB CD ⊥==，且平面BDFE ⊥平面ABCD ．（1）求证：AC ⊥平面BDFE ； （2）若BF 与平面ABCD 所成角为4π，求二面角B DF C --的余弦值．20. 已知中心在原点O ，焦点在x 轴上，离心率为3的椭圆过点3⎭． （1）求椭圆的方程；（2）设椭圆与y 轴的非负半轴交于点B ，过点B 作互相垂直的两条直线，分别交椭圆于,P Q 两点，连接PQ ，求BPQ ∆的面积的最大值． 21. 已知函数()()22ln f x x x mx m R =+-∈．（1）若()f x 在其定义域内单调递增，求实数m 的取值范围； （2）若1752m <<，且()f x 有两个极值点()1212,x x x x <，求()()12f x f x -的取值范围． 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程已知在平面直角坐标系xOy 中，直线l 的参数方程是26x ty t =⎧⎨=+⎩（t 是参数），以原点O 为极点，x 轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线C 的极坐标方程为ρθ=．（1）求直线l 的普通方程与曲线C 的直角坐标方程； （2）设(),M x y 为曲线C 上任意一点，求x y +的取值范围． 23.选修4-5：不等式选讲 已知函数()12f x x x a =+++． （1）当4a =-时，求()f x 的最小值；（2）若2a >时，()7f x ≥对任意的,12a x ⎡⎤∈--⎢⎥⎣⎦恒成立，求a 的取值范围．试卷答案一、选择题1-5ABDAA 6-10 BCBCA 11、12：AB 二、填空题13. 2 14. 1515. 20x y +-=16. (三、解答题17.解：（1）因为2211n n n n a a a a +-+=-，所以，()()1110n n n n a a a a +++--=，因为10,0n n a a ->>，所以10n n a a -+≠，所以11n n a a --=， 所以{}n a 是以1为首项，1为公差的等差数列，所以n a n =， 当2n ≥时，12n n n b S S n -=-=，当1n =时，12b =也满足，所以2n b n =； （2）由（1）可知()1111112121n na b n n n n -⎛⎫==- ⎪++⎝⎭，所以()11111111222334121n n n T n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-= ⎪ ⎪ ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦． 18.解：（1）记事件A 为“从表1的日期中随机选出一天，这一天的升旗时刻早于7：00”，在表1的20个日期中，有15个日期的升旗时刻早于7：00，所以()153204P A ==； （2）X 可能的取值为0，1，2，记事件B 为“从表2的日期中随机选出一天，这一天的升旗时刻早于7：00” 则()()()512;11533P B P B P B ===-=；()()()409P X P B P B ===；()1211411339P X C ⎛⎫⎛⎫==-= ⎪⎪⎝⎭⎝⎭；()()()129P X P B P B ===， 所以X的分布列为：()44120129993E X =⨯+⨯+⨯=，（注：学生得到12,3X B ⎛⎫⎪⎝⎭，所以()12233E X =⨯=，同样给分）；（3）220s s <．19.解：（1）∵平面BDFE ⊥平面ABCD ，BE BD ⊥，平面BDFE 平面ABCD BD =，∴BE ⊥平面ABCD ，又AC ⊂平面ABCD ，∴AC BE ⊥， 又∵AC BD ⊥，且BE BD B =，∴AC ⊥平面BDFE ；（2）设ACBD O =，∵四边形ABCD 为等腰梯形，,242DOC AB CD π∠===，∴OD OC OB OA ====，∵//OB FE ，∴四边形BOFE 为平行四边形，∴//OF BE ， 又∵BE ⊥平面ABCD ，∴OF ⊥平面ABCD ， ∴FBO ∠为BF 与平面ABCD 所成的角，∴4FBO π∠=，又∵2FOB π∠=，∴OF OB ==以O 为原点，OA 为x 轴，OB 为y 轴，OF 为z 轴，建立空间直角坐标系，则()()(()(),0,,,,B D F C A ，()()0,2,22,2,DF CD ==，∵AC ⊥平面BDFE ，∴平面BDF 的法向量为()1,0,0， 设平面DFC 的一个法向量为(),,n x y z =，由00DF n CD n ⎧=⎪⎨=⎪⎩得00+==⎪⎩，令2x =得，()2,2,1n =-， 2222cos ,31221n AC ==++，∴二面角B DF C --的余弦值为23． 20.解：（1）由题意可设椭圆方程为()222210x y a b a b +=>>，则2232719c a a b ⎧=⎪⎪⎨⎪+=⎪⎩， 故31a b =⎧⎨=⎩，所以，椭圆方程为2219x y +=；（2）由题意可知，直线BP 的斜率存在且不为0，故可设直线BP 的方程为1y kx =+，由对称性，不妨设0k >，由221990y kx x y =+⎧⎨+-=⎩，消去y 得()2219180k x kx ++=，则BP =0k >换成1k-，得：BQ =，2222221118118122199211621829APQ k k k S BP BQ k k k k k k ∆++===++⎛⎫==+ ⎪⎛⎫⎝⎭++ ⎪⎝⎭⎝⎭设1k t k+=，则2t ≥， 故2162162276496489BPQ t S t t t∆==≤=++，取等条件为649t t =，即83t =， 即183k k +=，解得k =时，BPQ S ∆取得最大值278． 21.解：（1）()f x 的定义域为()0,+∞，()22f x x m x'=+-， ()f x 的定义域内单调递增，则()220f x x m x'=+-≥， 即22m x x≤+在()0,+∞上恒成立， 由于224x x+≥，所以4m ≤，实数m 的取值范围是(],4-∞；（2）由（1）知()22222x mx f x x m x x -+'=+-=，当1752m <<时()f x 有两个极值点，此时12120,12mx x x x +=>=，∴1201x x <<<， 因为1111725,2m x x ⎛⎫⎛⎫=+∈ ⎪ ⎪⎝⎭⎝⎭，解得11142x <<，由于211x x =，于是()()()()22121112122ln 2ln f x f x x mx x x mx x -=-+--+()()()222121212112112ln ln 4ln x x m x x x x x x x =---+-=-+， 令()2214ln h x x x x=-+，则()()222210x h x x--'=<，∴()h x 在11,42⎛⎫ ⎪⎝⎭上单调递减，()1124h h x h ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭，即()()()()121141ln 2161ln 2416f x f x --<-<--， 故()()12f x f x -的取值范围为152554ln 2,16ln 2416⎛⎫-- ⎪⎝⎭． 22.解：（1）由26x ty t =⎧⎨=+⎩，得26y x =+，故直线l 的普通方程为260x y -+=，由ρθ=，得2cos ρθ=，所以22x y +=，即(222x y -+=，故曲线C的普通方程为(222x y +=；（2）据题意设点)Mθ，则2sin 4x y πθθθ⎛⎫--+=+ ⎪⎝⎭，所以x y +的取值范围是2⎡-⎣．23.解：（1）当4a =-时，()124f x x x =++-， 当1x ≤-时，()12433f x x x x =---+=-+； 当12x -<<时，()1245f x x x x =+-+=-+； 当2x ≥时，()12433f x x x x =++-=-；即()33,15,1233,2x x f x x x x x -+≤-⎧⎪=-+-<<⎨⎪-≥⎩，又因为()f x 在(),1-∞-上单调递减，在()1,2-上单调递减，在()2,+∞上单调递增，如图所示，所以当2x =时，()f x 有最小值3；（2）因为,12a x ⎡⎤∈--⎢⎥⎣⎦，所以10,20x x a +≤+≥，则()()()1217f x x x a x a =-+++=+-≥，可得8a x ≥-+对任意,12a x ⎡⎤∈--⎢⎥⎣⎦恒成立，即82a a ⎛⎫≥--+ ⎪⎝⎭，解得16a ≥，故a 的取值范围为[)16,+∞.。

河北省武邑中学2018届高三上学期第五次调研考试数学（文）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. ）B. C. D.【答案】D【解析】故选D2. ）【答案】D化简得到故答案为：D。

3. ）A. B.C. D.【答案】B故排除A选项，B是正确的。

故答案为：B。

4. ）A. 2B. 1【答案】C【解析】,，选C.5. 的图象与轴的两个相邻交点的距离等于若将函数则在下列区间中使的是（）【答案】B【解析】∵函数f（x）=sinωx（ω＞0）的图象与x轴的两个相邻交点的距离等于函数f（x）=sin4x若将函数y=f（x个单位得到函数y=g（x）=2sin（令k∈Z，当k=0时，故函数g（x）的减区间为。

故答案为B 。

6. 上所有点向右平移标缩短为原来的，得到曲线）A. 对称B.C. 对称对称【答案】B【解析】由题意可得，曲线的对称轴；时，，故；时，不是的对称中心；本题选择B选项.7. ）A. 20B. 42C. 60D. 180【答案】C【解析】结合流程图可知，该程序运行过程如下：首先初始化数据：第一次循环：不满足第二次循环：不满足第三次循环：不满足第四次循环：满足程序跳出循环，输出的值为本题选择C选项.点睛：此类问题的一般解法是严格按照程序框图设计的计算步骤逐步计算，逐次判断是否满足判断框内的条件，决定循环是否结束．要注意初始值的变化，分清计数变量与累加(乘)变量，掌握循环体等关键环节．8.其中正确命题的序号是（）A. ①③B. ③④C. ①④D. ②③【答案】B【解析】①n在平面内。

故不正确的。

故正确的是③④。

故答案为：B。

9. ）C.【答案】D【解析】对于A A错；对于B则，故B错；对于CC错；对于D：=D对；故选D10. ）A. B.C. D.【答案】A【解析】由y轴对称，故可排除B，D．又当x=2时，y=-2•（-2）2+22=-4．所以，C是错误的，故选A．11. 相交于,若）D. 6【答案】A【解析】由题设知抛物线y2=2px的准线为 y=±由双曲线的对称性知△MNF为等腰直角三角形，∴∠tan∠故选A.点睛：本题考查了抛物线的标准方程及双曲线的对称性应用，关键是分析出△MNF为等腰直角三角形，利用tan∠FMN=1建立等式即可解出.12. 的导函数，时，）【答案】A【解析】设g（x）g（x）的导数为：g′（x）x＞0时，xf′（x）-f（x）＞0，即当x＞0时，g′（x）恒大于0，∴当x＞0时，函数g（x）为增函数，∵f（x）为奇函数∴函数g（x）为定义域上的偶函数又∵g（-1）f（x）＞0，∴当x＞0时，当x＜0∴当x＞0时，g（x）＞0=g（1），当x＜0时，g（x）＜0=g（-1），∴x＞1或-1＜x＜0故使得f（x）＞0成立的x的取值范围是（-1，0）∪（1，+∞），故选A.点睛：本题主要考查了利用导数判断函数的单调性，并由函数的奇偶性和单调性解不等式，g（x）.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 垂直，则__________．【答案】【解析】根据题意得到垂直，根据向量垂直的坐标表示得到（）*故答案为：点睛：这个题目考查的是向量基本定理的应用；向量的点积运算。

河北武邑中学2017—2018学年高三年级上学期期末考试数学试题（文）第Ⅰ卷（选择题 共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{}{}2|lgx 0,|4M x N N x =>=≤，则M N ⋂（ ） A ． []1,2 B ．()1,2 C ．[)1,2 D ．(]1,22.设复数z 满足243z i i -=+，则z =（ ）A ．44i +B ．44i -C ．22i -D ．22i +3.已知函数()log 2a y ax =-在[]0,1上是x 的函数，则a 的取值范围是（ ） A ．()0,1 B ．()1,2 C ．()0,2 D ．[)2,+∞4. 已知数列{}n a 满足：()111,212n n a a a n -==+≥，为求使不等式123n a a a a k ++++<的最大正整数n ，某人编写了如图所示的程序框图，在框图的判断框中的条件和输出的表达式分别为（ ）A ．,S k i <B ．,1S k i <- C. ,S k i ≥ D ．,1S k i ≥-5.设实数,x y 满足3010210x y y x x +-≤⎧⎪⎪-≥⎨⎪-≥⎪⎩，则y x u x y =-的取值范围为（ ）A ．1,22⎡⎤⎢⎥⎣⎦B ．2,23⎡⎤-⎢⎥⎣⎦C. 23,32⎡⎤-⎢⎥⎣⎦ D ．33,22⎡⎤-⎢⎥⎣⎦6.有编号为1，2，…，700的产品，现需从中抽取所有编号能被7整除的产品为样品进行检验.下面是四位同学设计的程序框图，其中正确的是（ ）A． B．C. D．7.某几何体的三视图如图所示，则该几何体的体积为（）A ．643π+．563π+18π D ．224π+ 8.如图，周长为1的圆的圆心C 在y 轴上，顶点()0,1A ，一动点M 从A 开始逆时针绕圆运动一周，记走过的弧长AB x =，直线AM 与x 轴交于点(),0N t ，则函数()t f x =的图像大致为（ ）A ．B ．C. D ．9.某工厂生产甲、乙两种产品，生产甲产品1件需消耗原料1千克，原料2千克；生产乙产品1件需消耗原料2千克，原料1千克；每件甲产品的利润是300元，每件乙产品的利润是400元，公司在生产这两种产品的计划中，要求每天消耗，原料都不超过12千克，通过合理安排计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是（ ） A ． 1800元 B ． 2400元 C. 2800元 D ．3100元 10.圆心在曲线()30y x x=>上，且与直线3430x y ++=相切的面积最小的圆的方程为（ ） A ． ()223292x y ⎛⎫-+-= ⎪⎝⎭ B ． ()()22216315x y ⎛⎫-+-= ⎪⎝⎭C. ()()22218135x y ⎛⎫-+-= ⎪⎝⎭D ．((229x y -+-=11.一个几何体的三视图如图所示，该几何体外接球的表面积为（ ）A ．36πB ．1123π C. 32π D ．28π 12.若12,F F 为双曲线22221x y a b-=的左右焦点，O 为坐标原点，点P 在双曲线的左支上，点M 在双曲线的右准线上，且满足：()111,0OF OM FO PM OP OF OM λλ⎛⎫ ⎪==+>⎪⎝⎭，则该双曲线的离心率为 （ ）A ．3第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上 13.平面向量a 与b 的夹角为60°，()2,0,1a b ==，则2a b += ． 14.已知某几何体的三视图如图所示，则这个几何体的体积为 ．15.甲、乙两艘轮船都要在某个泊位停靠4小时，假定它们在一昼夜的时间中随机地到达，则两艘船中至少有一艘在停靠泊位时必须等待的概率为 ．16. ABC ∆中，角,,A B C 所对的边分别为,,a b c ，向量()()2,1,2,cos q a p b c C ==-，且//p q ，三角函数式2cos 2C11tan Cμ-=++的取值范围是 ．三、解答题 ：共70分.解答应写出文字说明、证明过程或演算步骤. 第17-21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.17.已知数列{}n a ，{}n b 满足：()()111,1,411n n n n n n b a a b b a a -=+==-+．（1）设11n n C b =-，求数列{}n C 的通项公式； （2）设12231n n n S a a a a a a +=+++，不等式4n n aS b <恒成立时，求实数a 的取值范围．18.如图，在四棱锥P ABCD -中，底面ABCD 是边长为a 的正方形，E F 、分别为PC BD 、的中点，侧面PAD ⊥底面ABCD，且PA PD AD ==． （1）求证：//EF 平面PAD ； （2）求三棱锥C PBD -的体积．19.某企业为了对新研发的一批产品进行合理定价，将产品按事先拟定的价格进行试销，得到一组销售数据()(),1,2,6i i x y i =，如表所示：（1）求q 的值；（2）已知变量,x y 具有线性相关性，求产品销量y 关于试销单价x 的线性回归方程ˆˆˆybx a =+可供选择的数据662113050,271i i i i i x y x ====∑∑；（3）用ˆy表示（2）中所求的线性回归方程得到的与对应的i x 产品销量的估计值.当销售数据()(),1,2,6i i x y i =对应的残差的绝对值时，则将销售数据ˆ1i i yy -≤称为一个“好数据”.试求(),i i x y 这6组销售数据中的“好数据”.参数数据：线性回归方程中的ˆˆ,ba 最小二乘估计分别是()1221ˆˆˆ,ni ii nii x y nx yb ay bx xn x==-==--∑∑ 20.已知抛物线()2:20C y px p =>在第一象限内的点()2,t P 到焦点的距离为52． （1）若1,02M ⎛⎫- ⎪⎝⎭，过点,M P 的直线1l 与抛物线相交于另一点Q ，求QF PF 的值；（2）若直线2l 与抛物线C 相交于,A B 两点，与圆()22:1M x a y -+=相交于,D E 两点，O 为坐标原点，OA OB ⊥，试问：是否存在实数a ，使得DE 的长为定值？若存在，求出的值；若不存在，请说明理由．21. 已知函数()()2112x f x x e ax =--．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程在直角坐标系xOy 中，曲线1C 的参数方程为1cos sin x y αα=+⎧⎨=⎩（α为参数，0πα-<<），曲线2C 的参数方程为1225x t y ⎧=-⎪⎨⎪=+⎩（t 为参数），以O 为极点，x 轴的正半轴为极轴建立坐标系． （1）求曲线1C 的极坐标方程和曲线2C 的普通方程； （2）射线4πθ=-与曲线1C 的交点为P ，与曲线2C 的交点为Q ，求线段PQ 的长．23.选修4-5：不等式选讲 已知函数()1f x x =+． （1）解不等式()21f x x ≥+；（2）x R ∃∈，使()()26f x f x m --+<成立，求m 的取值范围．试卷答案一、选择题1-5DCBBA 6-10 BBDCA 11、12：CC 二、填空题13. 113616. (- 三、解答题17.解：（1）∵11112n n b b --=--，∴12111111n n n n b b b b --==-+---， ∵11141c b ==--，∴数列{}n c 是以-4为首项，-1为公差的等差数列，∴()()4113n c n n =-+--=--； （2）由（1）知，131n n c n b ==---，∴23n n b n +=+， 从而113n n a b n =-=+， ()()()12231111114556344444n n n n S a a a a a a n n n n +=+++=+++=-=⨯⨯++++， ∴()()()()21368244334n n n a n a n a n aS b n n n n -+-+-+-=-=++++， 由题意可知()()213680a n a n -+--<恒成立，即可满足不等式4n n aS b <恒成立， 设()()()21368f n a n a n =-+--， 当1a =时，()380f n n =--<恒成立，当1a >时，由()()213680a n a n -+--=的判别式()()2363210a a ∆=-+->， 再结合二次函数的性质4n n aS b <不可能成立； 当1a <时，对称轴()323110,2121a n f n a a -⎛⎫=-=--< ⎪--⎝⎭在()1,+∞上为单调递减函数，∵()()()113684150f a a a =-+--=-<， ∴1a <时，4n n aS b <恒成立， 综上知：当1a ≤时，4n n aS b <恒成立．18.解：（1）连结AC ，则F 是AC 的中点，E 为PC 的中点， 故在CPA ∆中，//EF PA ，且PA ⊂平面PAD ，EF ⊄平面PAD ， ∴//EF 平面PAD ；（2）取AD 的中点N ，连结PN ，∵PA PD =，∴PN AD ⊥， 又平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =， ∴PN ⊥平面ABCD ， ∴31111332212C PBD P BCDBCD a V V S PN a a a --∆====. 19.解：（1）∵84838075686q y +++++=，又∵80y =，∴8483807568806q +++++=，∴90q =；（2）4567891362x +++++==，∴21330506802ˆ41327162b-⨯⨯==-⎛⎫- ⎪⎝⎭， ∴()13ˆ8041062a=--⨯=， ∴ˆ4106yx =-+； （3）∵ˆ4106yx =-+， ∴1111ˆˆ410690,909001yx y y =-+=-=-=<，所以()()11,4,90x y =是好数据； 2222ˆˆ410686,868421yx y y =-+=-=-=>，所以()()22,5,84x y =不是好数据； 3333ˆˆ410682,838211yx y y =-+=-=-==，所以()()33,6,83x y =是好数据； 4444ˆˆ410678,788021yx y y =-+=-=-=>，所以()()44,7,80x y =不是好数据； 5555ˆˆ410674,757411yx y y =-+=-=-==，所以()()55,8,75x y =是好数据； 6666ˆˆ410670,706821yx y y =-+=-=-=>，所以()()66,9,68x y =不是好数据； 所以好数据为()()()4,90,6,68,8,75. 20.解：（1）∵点()2,P t ，∴5222p +=，解得1p =， 故抛物线C 的方程为：22y x =，当2x =时，2t =， ∴1l 的方程为4255y x =+，联立可得212,8Q y x x ==， 又∵11,22Q P QF x PF x =+=+，∴111821422QF PF +==+；（2）设直线AB 的方程为x ty m =+，代入抛物线方程可得2220y ty m --=， 设()()1122,,A x y B x y ，则12122,2y y t y y m +==-，① 由OA OB ⊥得：()()12120ty m ty m y y +++=， 整理得()()22121210t y y tm y y m ++++=，② 将①代入②解得2m =，∴直线:2l x ty =+，∵圆心到直线l的距离d =，∴DE =显然当2a =时，2,DE DE =的长为定值. 21.解：（1）()()()1x x x f x e x e ax x e a '=+--=-， ①设0a ≤，则当(),0x ∈-∞时，()0f x '<；当()0,x ∈+∞时，()0f x '>，所以()f x 在(),0-∞单调递减，在()0,+∞单调递增； ②设0a >，由()0f x '=得0x =或ln x a =， 若1a =，则()()10x f x x e '=-≥， 所以()f x 在(),-∞+∞单调递增， 若01a <<，则l n 0a <，故当()(),ln 0,x a ∈-∞+∞时，()0f x '>；当()l n ,0x a∈时，()0f x '<， 所以()f x 在()(),ln ,0,a -∞+∞单调递增，在()ln ,0a 单调递减； ③若1a >，则l n 0a >，故当()(),0ln ,x a ∈-∞+∞时，()0f x '>；当()0,l n x a ∈时，()0f x '<，所以()f x 在()(),0,ln ,a -∞+∞单调递增，在()0,ln a 单调递减；综上所述，当0a ≤时，()f x 在(),0-∞单调递减，在()0,+∞单调递增；当01a <<时()f x 在()(),ln ,0,a -∞+∞单调递增，在()0,ln a 单调递减；（2）①设0a ≤，则由（1）知，()f x 在(),0-∞单调递减，在()0,+∞单调递增， 又()()01,1f f a =-=-，取b 满足3b <-且()ln b a =-，则()()()221220f b a b ab a b b >---=-+->，所以()f x 有两个零点；②设1a =，则()()1x f x x e =-，所以()f x 只有一个零点；③设01a <<，则由（1）知，()f x 在()(),ln ,0,a -∞+∞单调递增，在()ln ,0a 单调递减，()01f =-，当ln b a =时，()f x 有极大值()()()221220f b a b ab a b b =--=--+<，故()f x 不存在两个零点；当1a >时，则由（1）知，()f x 在()(),0,ln ,a -∞+∞单调递增，在()0,ln a 单调递减，当0x =时，()f x 有极大值()010f =-<，故()f x 不存在两个零点， 综上，a 的取值范围为0a ≤.22.解：（1）曲线1C 的参数方程为1cos sin x y αα=+⎧⎨=⎩（α为参数，0πα-<<），普通方程为()()22110x y y -+=<，极坐标方程为2cos ,,02πρθθ⎛⎫=∈- ⎪⎝⎭，曲线2C的参数方程为125x y ⎧=⎪⎨⎪=+⎩（t 为参数）， 普通方程260x y +-=； （2）,4πθρ=-=，即4P π⎫-⎪⎭；4πθ=-代入曲线2C的极坐标方程，可得ρ'=4Q π⎛⎫- ⎪⎝⎭，∴PQ ==23.解：（1）当10x +≥即1x ≥-时，121x x +≥+，∴10x -≤≤， 当10x +<即1x <-时，121x x --≥+，∴1x <-， ∴不等式的解集为{}|0x x ≤；（2）∵()()21,67f x x f x x -=-+=+，∴17x x m --+<，∵x R ∃∈，使不等式17x x m --+<成立，∴m 大于17x x --+的最小值， ∴8m >-.。

2018届河北省武邑中学高三上学期第四次调研考试数学（文）试题一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一 项是符合题目要求的。

1．已知R 是实数集，集合{3|1,|M x N y y x x ⎧⎫=<==+⎨⎬⎩⎭，则()R N C M = （ ） A ．[]0,2 B ．[)2,+∞ C ．(],2-∞ D ．[]2,32.为了有效管理学生迟到问题，某校专对各班迟到现象制定了相应的等级标准，其中D 级标准为“连续10天，每天迟到不超过7人”，根据过去10天1、2、3、4班的迟到数据，一定符合D 级标准的是( ) A ．1班：总体平均值为3，中位数为4 B ．2班：总体平均值为1，总体方差大于0 C ． 3班：中位数为2，众数为3D ． 4班：总体平均值为2，总体方差为33.已知函数f (x )＝是定义域上的递减函数，则实数a 的取值范围是( )A ． (，)B ． (，]C ． [，)D ． (，]4.集合{x |x 2－ax －2＝0，a ∈R }的真子集个数是( )A ． 4B ． 3C ． 1D ． 与a 的取值有关5.针对柱、锥、台、球，给出下列命题①如果一个几何体的三视图是完全相同的，则这个几何体是正方体； ②如果一个几何体的正视图和俯视图都是矩形，则这个几何体是长方体； ③如果一个几何体的三视图都是矩形，则这个几何体是长方体；④如果一个几何体的正视图和侧视图都是等腰梯形，则这个几何体是圆台． 其中正确的是( ) A ． ①②B ． ③C ． ③④D ． ①③6.已知,m n 为两条不同的直线，,αβ为两个不同的平面，给出下列4个命题： ①若,//,//m n m n αα⊂则 ②若,//,m n m n αα⊥⊥则 ③若,,//m m αβαβ⊥⊥则 ④若//,//,//m n m n αα则 其中真命题的序号为（ ）A ．①②B ．①④C ．③④D ．②③7.在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≥≤--≥-0033023y y x y x , 表示的平面区域的面积是（ ） A.32 B. 3 C. 2 D. 238.运行右边的程序框图,如果输入的[1,3]t ∈-,则输出s 属于（ ）A ．[2,5]-B ．[5,2]-C ．[4,3]-D ．[3,4]-9.已知,31:-<>x x p 或 a x q >:，若q 是p 的充分不必要条件，则a 的取值范围是( ) A ．[1，＋∞) B ．(－∞，1] C ．[－3，＋∞) D ．(－∞，－3] 10、已知各项均为正的等比数列{}n a ，公比为q ，前n 项和为n S ，则“1q >”是“26423S S S +>”的（ ） A 、充分不必要条件 B 、必要不充分条件 C 、充要条件 D 、既不充分也不必要条件11、已知函数()()32,f x ax ax x b a b R =+++∈，则下列图象一定不能表示()f x 的图象的是（ ）12已知定义在R 的函数()f x 是偶函数，且满足()()[]2202f x f x +=-，在，上的解析式为()21,011,12x x f x x x ⎧-≤<=⎨-≤≤⎩，过点()3,0-作斜率为k 的直线l ，若直线l 与函数()f x 的图象至少有4个公共点，则实数k 的取值范围是 A ．11,33⎛⎫- ⎪⎝⎭B．1,63⎛-+ ⎝C．1,63⎛-- ⎝D．163⎛⎫- ⎪⎝⎭二、填空题(共4小题,每小题5.0分,共20分)13. 求函数y ＝sin 的单调区间为________．14. 曲线x y ln =在点(,1)M e 处的切线方程为______________.15.当0>x 时，不等式032>+-mx x 恒成立，则实数m 的取值范围是__________.16．若函数()2xf x e x a =--在R 上有两个零点，则实数a 的取值范围是__________.三、解答题（本题共6小题，共70分）17、（10分）已知函数()()2sin cos cos 20f x x x x ωωωω=⋅+>的最小正周期为π. （1）求ω的值； （2）求()f x 的单调递增区间.18.(本小题满分12分)已知数列{}n a 的前n 项和为()211,5,1n n n S a nS n S n n +=-+=+.(I)求证：数列n S n ⎧⎫⎨⎬⎩⎭为等差数列； (II)令2nn n b a =，求数列{}n b 的前n 项和n T ． 19．(本小题满分12分)某省电视台为了解该省卫视一档成语类节目的收视情况，抽查东西两部各5个城市，得到观看该节目的人数(单位：千人)如下茎叶图所示，其中一个数字被污损． (I)求东部观众平均人数超过西部观众平均人数的概率.(II)节目的播出极大激发了观众随机统计了4位观众的周均学习成语知识的的时间y (单位：小时)与年龄x (单位：岁)，并制作了对照表(如下表所示)：由表中数据分析，x ，y 呈线性相关关系，试求线性回归方程 y bxa =+ ，并预测年龄为60岁观众周均学习成语知识的时间．参考数据：线性回归方程中 ,ba 的最小二乘估计分别是()1221,ni ii ni i x y nxyb ay bx x n x==-==--∑∑ ． 20.（本小题满分12分）在ABC ∆中，内角A B C ，，的对边分别为a b c ，，，已知cos 2cos 2cos A C c aB b--=． （I ）求sin sin C A 的值； （II ）若1cos 24B b ==，，求ABC ∆的面积S ． 21.（本小题满分12分）已知函数ln ()()x kf x k R x x=-∈的最大值为()h k . （I ）若1k ≠，试比较()h k 与21k e的大小；（II ）是否存在非零实数a ，使得()kh k ae>对k R ∈恒成立，若存在，求a 的取值范围；若不存在，说明理由.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程（本小题满分10分） 在直角坐标系xOy 中，圆1C 和2C 的参数方程分别是22cos 2sin x y ϕϕ=+⎧⎨=⎩（ϕ为参数）和cos 1sin x y ββ=⎧⎨=+⎩（β为参数），以O 为极点，x 轴的正半轴为极轴建立极坐标系. （Ⅰ）求圆1C 和2C 的极坐标方程；（Ⅱ）射线OM ：θα=与圆1C 交于点O 、P ，与圆2C 交于点O 、Q ，求||||OP OQ ⋅ 的最大值. 23．[选修4—5：不等式选讲](10分)已知函数(),f x x a a R =-∈(I)当1a =时，求()11f x x ≥++的解集；(II)若不等式()30f x x +≤的解集包含{}1x x ≤-，求a 的取值范围．四调数学（文）试题答案1. D2. D3. B4. B5. B6. D7. A8. D9. A 10. A 11. D 12. C13.(k ∈Z)．14.0=-ey x 15.)32,(-∞ 16.),2ln 22(+∞-17、解：（1）由()2sin cos cos 2f x x x x ωωω=⋅+ =sin 2cos 2x x ωω+24x πω⎛⎫+ ⎪⎝⎭22T ππω∴==得1ω=（2）由（1）的()24f x x π⎛⎫=+ ⎪⎝⎭依题可得()222242k x k k Z πππππ-+≤+≤+∈得()388k x k k Z ππππ-+≤≤+∈ ()f x ∴的单调递增区间为()3,88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦18. 解：⑴由()n n S n nS n n +=+-+211得111=-++nS n S nn ……………………………………3分 又511=S ，所以数列⎭⎬⎫⎩⎨⎧n S n 是首项为5，公差为1的等差数列…………………………4分 ⑵由⑴可知()415+=-+=n n nS n所以n n S n 42+=…………………………………5分 当2≥n 时，()()321414221+=----+=-=-n n n n n S S a n n n又1a 也符合上式，所以()*32N n n a n ∈+=……………………………………………6分所以()nn n b 232+= ……………………………………………………7分所以()nn n T 23229272532++⋯⋯+⋅+⋅+⋅=()()13322322122927252+++++⋯⋯+⋅+⋅+⋅=n n n n n T所以()()()22122221023211431-+=+⋯⋯++--+=+++n n n n n n T…………………………12分。

河北省衡水市武邑中学2018届高三（上）第三次调研数学试卷（文科）一、选择题：本题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求．1．（5分）已知集合A={x|（x﹣2）（x+6）＞0}，B={x|﹣3＜x＜4}，则A∩B等于（）A．（﹣3，﹣2）B．（﹣3，2）C．（2，4）D．（﹣2，4）2．（5分）设向量，则与垂直的向量可以是（）A．（4，﹣6）B．（3，﹣2）C．（4，6）D．（3，2）3．（5分）若=，则tan2α的值为（）A．B．C．﹣D．34．（5分）已知等比数列{a n}满足a1=+3，则a9=（）A．B．C．648 D．185．（5分）若变量x，y满足约束条件，则目标函数z=2x+y的最小值为（）A．4 B．﹣1 C．﹣2 D．﹣36．（5分）设等差数列{a n}的前n项和是S n，若﹣a m＜a1＜﹣a m+1（m∈N*，且m≥2），则必定有（）A．S m＞0，且S m+1＜0 B．S m＜0，且S m+1＞0C．S m＞0，且S m+1＞0 D．S m＜0，且S m+1＜07．（5分）已知a＞b＞0，a+b=1，x=﹣（）b，y=log（ab）（+），z=log b，则（）A．y＜x＜z B．x＜z＜y C．z＜y＜x D．x＜y＜z 8．（5分）函数f（x）=A sin（ωx+φ）（A＞0，ω＞0，）的图象如图所示，将f（x）的图象向右平移m个单位得到g（x）的图象关于y轴对称，则正数m的最小值为（）A．B．C．D．9．（5分）定义在R上的函数f（x），满足f（x+5）=f（x），当x∈（﹣3，0]时，f（x）=﹣x﹣1，当x∈（0，2]时，f（x）=log2x，则f（1）+f（2）+f（3）+…f（2018）的值等于（）A．403 B．405 C．806 D．80910．（5分）如图，平行四边形ABCD中，AB=2，AD=1，∠A=60°，点M在AB边上，且AM= AB，则等于（）A．﹣1 B．1 C．﹣D．11．（5分）黑板上有一道有正解的解三角形的习题，一位同学不小心把其中一部分擦去了，现在只能看到：在△ABC中，角A、B、C的对边分别为a、b、c，已知a=2，…，解得，根据以上信息，你认为下面哪个选项可以作为这个习题的其余已知条件（）A．A=30°，B=45°B．C．B=60°，c=3 D．C=75°，A=45°12．（5分）已知f（x）=[x2﹣（a﹣3）x﹣b]（2x﹣），当x＜0时，f（x）≤0，则a的取值范围为（）A．a≥2 B．a≤2 C．a＜2 D．0＜a＜2二、填空题：本大题共4小题，每小题5分，共20分13．（5分）已知向量与的夹角为，，则=．14．（5分）若函数的图象关于直线对称，则函数f（x）的最大值为．15．（5分）已知函数，若函数g（x）=f（x）+3m有3个零点，则实数m的取值范围是．16．（5分）在希腊数学家海伦的著作《测地术》中记载了著名的海伦公式，利用三角形的三条边长求三角形面积，若三角形的三边长为a，b，c，其面积，这里．已知在△ABC中，BC=6，AB=2AC，则△ABC面积的最大值为．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤. 17．（10分）设函数（1）求函数f（x）的最大值，并写出使f（x）取最大值时x的集合；（2）已知△ABC中，角A、B、C的边分别为a、b、c，若，求a 的值．18．（12分）设等比数列{a n}的前n项和为S n，3a7=a42，a2=2a1，在等差数列{b n}中，b3=a4，b15=a5（1）求证：S n=2a n﹣3；（2）求数列{}的前n项和T n．19．（12分）已知在△ABC中，角A、B、C的对边分别为a、b、c，，a=4，c=5 （1）求边b的长；（2）若＞1，点E、F分别在线段AB、AC上，当S△AFE=时，求△AFE的周长的最小值．20．（12分）已知数列{a n}的各项均是正数，其前n项和为S n，且S n=4﹣a n（1）求数列{a n}的通项公式；（2）设，求数列{b n}的前2n项和T2n．21．（12分）已知函数f（x）=x3﹣2mx2﹣3nx+4m2在x=1处有极值10．（1）求实数m，n的值；（2）设，讨论函数f（x）在区间[a，a+1]上的单调性．22．（12分）已知函数f（x）=x2+t ln x﹣，（t∈R）t为常数（1）若函数y=f（x）在点（1，f（1））处的切线斜率为4，求函数f（x）的单调性．（2）若，且对∀x＞0都有g（x）+f（x）＞0，求实数t的取值范围．【参考答案】一、选择题1．C【解析】∵A={x|（x﹣2）（x+6）＞0}={x|x＜﹣6或x＞2}，B={x|﹣3＜x＜4}，∴A∩B={x|2＜x＜4}，故选：C．2．D【解析】∵向量，∴=（2，﹣3），在A中，（2，﹣3）•（4，﹣6）=26，故A错误；在B中，（2，﹣3）•（3，﹣2）=12，故B错误；在C中，（2，﹣3）•（4，6）=﹣10，故C错误；在D中，（2，﹣3）•（3，2）=0，故D正确．故选：D．3．D【解析】∵==，∴tanα=3，则tan2α===﹣，故选：D．4．D【解析】等比数列{a n}满足a1=+3，∴a52=2a5+3，解得a5=3或a5=﹣1（舍去）∵a1=，∴a9a1=a52=9，∴a9=18，故选：D5．C【解析】由约束条件作出可行域如图，A（﹣1，0），化目标函数z=2x+y为y=﹣2x+z，由图可知，当直线y=﹣2x+z过A时，直线在y轴上的截距最小，z有最小值为﹣2．故选：C．6．A【解析】∵﹣a m＜a1＜﹣a m+1，∴a1+a m＞0，a1+a m+1＜0∴＞0，＜0故选A7．D【解析】由题意a＞b＞0，a+b=1，∴1＞a＞0，1＞b＞0．不妨令a=，b=则x=﹣（）b＜﹣1，y=log（ab）（+）=﹣1，z=log b＞﹣1．∴x＜y＜z．故选D．8．C【解析】根据函数f（x）=A sin（ωx+φ）（A＞0，ω＞0，）的图象，可得A=1，=﹣，∴ω=2．再根据五点法作图可得2•+φ=，∴φ=．∴f（x）=sin（2x+）．将f（x）的图象向右平移m个单位得到g（x）=sin（2x﹣2m+）的图象关于y轴对称，∴﹣2m+=kπ+，∴m=﹣﹣，k∈Z，取k=﹣1，可得正数m的最小值为，故选：C．9．B【解析】∵f（x+5）=f（x），∴f（x）是周期为5的周期函数，f（3）=f（﹣2）=1，f（4）=f（﹣1）=0，f（5）=f（0）=﹣1，∴f（1）+f（2）+f（3）+f（4）+f（5）=1，∴f（1）+f（2）+f（3）+…+f（2018）=403[f（1）+f（2）+f（3）+f（4）+f（5）]+f（1）+f（2）+f（3）=403+0+1+1=405．故选B．10．B【解析】∵AM=AB，AB=2，AD=1，∠A=60°，∴∴=（）•（）===1+×4=1故选B11．D【解析】A.由a=2，sin30=，sin45=，根据正弦定理得：b==2≠，故此选项错误；B.由a=2，c=1，cos C=，利用余弦定理得：1=4+b2﹣b，即3b2﹣2b+9=0，∵△=4﹣108=﹣104＜0，所以此方程无解，故此选项错误；C.由a=2，c=3，cos B=，根据余弦定理得：b2=13﹣6=7，解得b=≠，故此选项错误；D.由B=180°﹣75°﹣45°=60°，又a=2，根据正弦定理得：=，则b=，故此选项正确，所以选项D可以作为这个习题的其余已知条件．故选D12．A【解析】令g（x）=x2﹣（a﹣3）x﹣b，∵当x＜﹣1时，2x﹣＜0，当﹣1＜x＜0时，2x﹣＞0，且当x＜0时，f（x）≤0，∴g（x）≥0在（﹣∞，﹣1）上恒成立，g（x）≤0在（﹣1，0）上恒成立．∴，即，解得a≥2．故选：A．二、填空题13．2【解析】∵向量与的夹角为，，∴可得：+4﹣4=12，即：4+4﹣4×2×||×cos=12，∴4||2﹣4||﹣8=0，解得：||=2．故答案为：2．14．【解析】函数=，其中tanθ=a．∵图象关于直线对称，∴sin（）=±1即=，k∈Z可得：θ=±kπ那么tan（±kπ）=1∴a=1．则f（x）的最大值为．故答案为：15．（﹣，0）【解析】作出y=f（x）的函数图象如图所示：∵g（x）=f（x）+3m有3个零点，∴0＜﹣3m＜1，解得﹣．故答案为：（﹣，0）．16．12【解析】∵a=6，设b=x，则c=2x，可得：=3+，∴===由三角形三边关系有：x+2x＞6且x+6＞2x，解得：2＜x＜6，故当x=2时，S△ABC取得最大值12．故答案为：12．三、解答题17．解：（1）∵函数=cos2x cos+sin2x sin+1+cos2x =cos2x﹣sin2x+1=cos（2x+）+1，故函数f（x）的最大值为2，此时，2x+=2kπ，即x=kπ﹣，k∈Z，故使f（x）取最大值时x的集合为{x|x x=kπ﹣，k∈Z}．（2）已知△ABC中，若f（B+C）=cos（2B+2C+）+1=cos（2π﹣2A+）+1=，∴cos（2A﹣）=．∵A∈（0，π），∴2A﹣∈（﹣，），∴2A﹣=，∴A=．再利用余弦定理可得a===．18．（1）证明：设等比数列{a n}的公比为q，∵3a7=a42，a2=2a1，∴=，q=2．解得a1=3．∴a n=3×2n﹣1，S n==3×2n﹣3．∴S n=2a n﹣3．（2）解：设等差数列{b n}的公差为d，b3=a4=3×23=24，b15=a5=3×24=48．∴48=24+12d，解得d=2．∴b n=24+2（n﹣3）=2n+18．==2．∴数列{}的前n项和T n=2+…+=2=．19．解：（1），由正弦定理可得=，即为2sin A cos A=2sin B cos B，即sin2A=sin2B，可得A=B或A+B=90°，当A+B=90°，可得b==3；当A=B时，可得b=a=4；（2）由a＞b，可得C=90°，b=3，cos A=，S△AFE==AE•AF•sin A=•bc sin A，可得AE•AF=bc=，由余弦定理可得EF===，△AFE周长l=AE+AF+≥2+=+，当且仅当AE=AF=时，周长取得最小值+．20．解：（1）由相减得a n=a n﹣1﹣a n，即又由S1=4﹣a1得a1=2，则数列{a n}是以为公比的等比数列（2），T2n=（b1+b3+…+b2n﹣1）+（b2+b4+…+b2n）=（﹣1+0+…+（2n﹣3））+（）==n2﹣2n+．21．解：（1）f（x）定义域为R，f'（x）=3x2﹣4mx﹣3n，∵f（x）在x=1处有极值10，∴f（1）′=0且f（1）=10，即，解得：或，当时，f′（x）=3（x﹣1）2≥0，当时，f（x）′=3x2+8x﹣11=（x﹣1）（3x+11），∴f（x）在x=1处有极值10时，．（2）由（1）可知f（x）=x3+4x2﹣11x+16，其单调性和极值分布情况如下表：∴①当且a+1≤1，即时，f（x）在区间[a，a+1]上的单调递减；②当a≤1＜a+1，即0＜a≤1时，f（x）在区间[a，1）上单调递减，在区间（1，a+1]上单调递增；③当a＞1时，f（x）在区间[a，a+1]上单调递增．综上所述，当时，函数f（x）在区间[a，a+1]上的单调性为：时，单调递减；0＜a≤1时，f（x）在[a，1]上单调递减，在[1，a+1]上单调递增；a＞1时，f（x）在[a，a+1]上单调递增．22．解：（1）∵f（x）=x2+t ln x﹣，∴f′（x）=，（x＞0），∴f′（1）=2+2t=4，解得：t=1，∴f′（x）=＞0，故f（x）在（0，+∞）递增；（2）令h（x）=g（x）+f（x），即h（x）=x2+tx+t ln x，①t=0时，f（x）=x2，当x＞0时，h（x）＞0成立，符合题意，②t＞0时，x→0时，ln x→﹣∞，t ln x→﹣∞，x2+tx→0，h（x）→﹣∞，即∀x＞0都有g（x）+f（x）＞0不成立，③t＜0时，由h（x）＞0，得＜﹣（+ln x），设g（x）=﹣（+ln x），则g′（x）=，令g′（x）＞0，解得：x＞1，令g′（x）＜0，解得：0＜x＜1，故g（x）在（0，1）递减，在（1，+∞）递增，故g（x）≥g（1）=﹣1，从而＜﹣1，即﹣1＜t＜0，综上，t的范围是（﹣1，0]．。