相量法
- 格式：ppt
- 大小：1.36 MB
- 文档页数：52
下载文档原格式
合集下载
第八章相量法
结论 任意一个正弦时间函数都有唯
一与其对应的复数函数。 一与其对应的复数函数。
i = 2 Icos( ωt + ϕ ) ↔ F ( t ) = 2 Ie
j ( ω t +ϕ )
17
§8-3 相量法的基础
i = 2 Icos( ωt + ϕ ) ↔ F ( t ) = 2 Ie
F(t)还可以写成 F ( t ) = 还可以写成
1 I= T
def
∫
∫
T
0
i 2 ( t )dt
可定义电压有效值： 可定义电压有效值： 电压有效值
1 U= T
def T 0
u 2 ( t )dt
13
§ 8-2
正弦量
正弦电流、 正弦电流、电压的有效值
设正弦电流 i = I m cos(ω t + φi )
1 T 2 I= I m cos 2 (ω t + φi ) dt T ∫0 = 1 I m = 0.707 I m 2
ejπ/2 =j , e-j π /2 = -j, 可以看成旋转因子。 可以看成旋转因子。
ejπ= –1 故 +j, –j, -1 都 1 j,
4
§ 8-2
1.正弦量： 正弦量： 正弦量
i + u _
正弦量
i
0
T
ωt
波形
瞬时值表达式
i(t) = I m cos( ω t + φi )
周期T 和频率f 周期 和频率
i、 I m 、 I ；
u、U m 、U
14
i = I m cos(ω t + φi ) = 2 Icos(ω t + φi ) u = U m cos(ω t + φu ) = 2U cos(ω t + φu )
相量法的运算公式
相量法的运算公式
相量的运算公式包括：
1.相量的加减法：
a+b = (a_x + b_x) + (a_y + b_y) j
a-b = (a_x - b_x) + (a_y - b_y) j
其中，a_x和a_y分别为向量a在x轴和y轴上的分量，b_x和b_y分别为向量b在x轴和y轴上的分量，j为虚数单位。
2.相量的乘法：
a*b = (a_magnitude * b_magnitude) * exp(j * (a_angle +
b_angle))
其中，a_magnitude和b_magnitude分别为向量a和b的模长，a_angle和b_angle分别为向量a和b与实部轴之间的夹角，exp为指数函数，j为虚数单位。
相量法拓展：
1.相量法不仅适用于平面向量，在空间向量中同样适用，只是需要增加z轴分量。
2.相量法不仅适用于电学领域中的交流电路分析，还适用于机械学、热力学的分析，以及计算机图形学中的向量运算等领域。
3.利用相量法，可以求解平面图形的面积、角度、垂直平分线、内心、外心等问题。
相量法
ω = 0(直流), X L = 0, 短路 ; ; ω → ∞, X L → ∞, 开路
ω
相量表达式: 相量表达式
& & & U = jX L I = jωLI ,
& = jB U = j − 1 U = 1 U & & & I L jωL ωL
返 回 上 页 下 页
波形图及相量图： 波形图及相量图：
返 回 上 页 下 页
电感元件VCR的相量形式 2. 电感元件 的相量形式
时域形式： 时域形式：
已知 i(t ) = 2I cos(ω t +ψi )
i(t) + uL(t) •
则
L
di(t ) uL (t ) = L = − 2ωL I sin(ω t +Ψ ) i dt π = 2ω L I cos(ω t +Ψ + ) i 2
uL O
pL i
2π π
& UL
电压超前电 流900
& I
ωt
Ψi
功率： 功率：
pL = uLi = ULm Im cos(ωt +Ψ ) sin(ω t +Ψ ) i i = UL I sin 2(ω t +Ψ ) i
瞬时功率以2ω交变，有正有负，一周期内刚好互相抵消 瞬时功率以 ω交变，有正有负，
返 回 上 页 下 页
波形图及相量图： 波形图及相量图： pR uR i
& UR
URI
& I
Ψu=Ψi
同 相 位
O
ωt
瞬时功率： 瞬时功率：
pR = uRi = 2UR 2I cos2 (ω t +Ψ i )
相量法
U
0
ωt
Ι
•
U = ωL I
15
感 抗
衡量电感线圈对交流电流阻碍 作用的物理量。 表示。 作用的物理量。用xL表示。
U x L = = ωL I
单位：欧姆（Ω） 单位：欧姆（
16
电路的功率
iu p
电感与电源只进行能量的周 期性交换， 期性交换，在一个周期内的 平均功率P为零 为零。 平均功率 为零。
UX ϕ = arctan UR
Z = R + (X L − X C )
2
2
X ϕ = arctan R
25
电阻、电感、电容串联电路
•
U
φ
•
U -U
L
•
•
S
C
Q
φ
U
2
R
P 功率三角形
2
U = U R + (U L − U C )
S = P2 + Q2
26
功率和功率因数
视在功率
交流电路中，电路端电压和电流有效值的乘 交流电路中， 积称为视在功率。 表示。 积称为视在功率。用S表示。 表示 单位：伏安（VA） 单位：伏安（ ）
1 ωL = ωC
ω0 =
1 LC
f0 =
1 2π LC
29
RL串联再与 并联的电路 串联再与C并联的电路 串联再与 I
R U
I1 I2
Đ2
φ2
C
Đy Đ Đ 1
φ１
•
U
L
Đω1
Đ
30
RL串联再与 并联的电路 串联再与C并联的电路 串联再与
1.XL ＜ XC 电感支路起主要作用,电路呈感性 电感支路起主要作用 电路呈感性 2.XL ＞ XC 电容支路起主要作用,电路呈容性 电容支路起主要作用 电路呈容性 3.XL ＝ XC 电路呈阻性，端电压与电流同相， 阻性，端电压与电流同相， 称为并联谐振。 称为并联谐振。 电流谐振
0
ωt
Ι
•
U = ωL I
15
感 抗
衡量电感线圈对交流电流阻碍 作用的物理量。 表示。 作用的物理量。用xL表示。
U x L = = ωL I
单位：欧姆（Ω） 单位：欧姆（
16
电路的功率
iu p
电感与电源只进行能量的周 期性交换， 期性交换，在一个周期内的 平均功率P为零 为零。 平均功率 为零。
UX ϕ = arctan UR
Z = R + (X L − X C )
2
2
X ϕ = arctan R
25
电阻、电感、电容串联电路
•
U
φ
•
U -U
L
•
•
S
C
Q
φ
U
2
R
P 功率三角形
2
U = U R + (U L − U C )
S = P2 + Q2
26
功率和功率因数
视在功率
交流电路中，电路端电压和电流有效值的乘 交流电路中， 积称为视在功率。 表示。 积称为视在功率。用S表示。 表示 单位：伏安（VA） 单位：伏安（ ）
1 ωL = ωC
ω0 =
1 LC
f0 =
1 2π LC
29
RL串联再与 并联的电路 串联再与C并联的电路 串联再与 I
R U
I1 I2
Đ2
φ2
C
Đy Đ Đ 1
φ１
•
U
L
Đω1
Đ
30
RL串联再与 并联的电路 串联再与C并联的电路 串联再与
1.XL ＜ XC 电感支路起主要作用,电路呈感性 电感支路起主要作用 电路呈感性 2.XL ＞ XC 电容支路起主要作用,电路呈容性 电容支路起主要作用 电路呈容性 3.XL ＝ XC 电路呈阻性，端电压与电流同相， 阻性，端电压与电流同相， 称为并联谐振。 称为并联谐振。 电流谐振
第八章 相量法
w 2 f 2 T
单位： rad/s ，弧度 / 秒 i Im O T 2
(3) 初相位(initial phase angle) i 反映正弦量的计时起点。
/w i
twt
同一个正弦量，计时起点不同，初相位不同。
i
一般规定：| | 。
O
t
=0 =－/2
二. 相位差 ：
T
0
1 cos 2(w t i ) 1 dt t 2 2
T 0
1 T 2
1 2 T Im I Im 0.707 I m T 2 2
i(t ) I m cos(w t i ) 2I cos(w t i )
Im 2I
同理，可得正弦电压有效值与最大值的关系：
u( t ) u1 ( t ) u2 ( t ) Re( 2 U 1 e Re( 2 U 1 e
可得其相量关系为：
jwt
) Re( 2 U 2 e jwt )
jwt
2U2 e
jwt
) Re( 2 (U 1 U 2 )e jwt )
U U1 U 2
相量的模表示正弦量的有效值
相量的幅角表示正弦量的初相位
同样可以建立正弦电压与相量的对应关系：
u( t ) 2U cos(w t θ ) U Uθ
例1 已知
i 141.4 cos(314t 30o )A u 311.1cos(314t 60o )V
试用相量表示i, u .
e cos j sin
指数形式
F=|F|（cos + jsin ）
相量法
15
1.正弦量的相量表示 设正弦电流 i 2 I cos(wt y i ) 复常数 构造复指数函数： F (t ) 2 Ie j(wt y i ) 2 Ie jy i e jwt +j 2Icos(wt y i ) j 2Isin( wt y i ) w
wt
Im
yi
O
+1
( 2) i1 ( t ) 10 cos(100 t 300 ) i2 ( t ) 10 sin(100 t 150 )
i2 (t ) 10 cos(100t 1050 )
j 300 (105 0 ) 135 0
i2 (t ) 3 cos( 100 t 150 0 )
e jwt ) Re( 2U e jwt ) u u1 u2 Re( 2U 1 2 e jwt 2U e jwt ) Re( 2 (U U )e jwt ) Re( 2U 1 2 1 2
U U U 1 2
相量加减运算：用代数式计算。
F1 F2 1 2
F1 F2 F1 e j1 F2 e j 2 F1 F2 e j(1 2 )
模相乘 角相加
F1 | F1 | θ1 | F1 | e jθ1 | F1 | j( θ1θ2 ) e jθ 2 F2 | F2 | θ2 | F2 | e | F2 | |F1| θ1 θ2 |F2|
Im I ，I m 2 I 2
13
同理，正弦电压有效值与最大值的关系：
Um U ，U m 2U 2
正弦电流、电压也可以表示为：
i 2I cos(wt y i )，u 2U cos(wt y u )
1.正弦量的相量表示 设正弦电流 i 2 I cos(wt y i ) 复常数 构造复指数函数： F (t ) 2 Ie j(wt y i ) 2 Ie jy i e jwt +j 2Icos(wt y i ) j 2Isin( wt y i ) w
wt
Im
yi
O
+1
( 2) i1 ( t ) 10 cos(100 t 300 ) i2 ( t ) 10 sin(100 t 150 )
i2 (t ) 10 cos(100t 1050 )
j 300 (105 0 ) 135 0
i2 (t ) 3 cos( 100 t 150 0 )
e jwt ) Re( 2U e jwt ) u u1 u2 Re( 2U 1 2 e jwt 2U e jwt ) Re( 2 (U U )e jwt ) Re( 2U 1 2 1 2
U U U 1 2
相量加减运算：用代数式计算。
F1 F2 1 2
F1 F2 F1 e j1 F2 e j 2 F1 F2 e j(1 2 )
模相乘 角相加
F1 | F1 | θ1 | F1 | e jθ1 | F1 | j( θ1θ2 ) e jθ 2 F2 | F2 | θ2 | F2 | e | F2 | |F1| θ1 θ2 |F2|
Im I ，I m 2 I 2
13
同理，正弦电压有效值与最大值的关系：
Um U ，U m 2U 2
正弦电流、电压也可以表示为：
i 2I cos(wt y i )，u 2U cos(wt y u )
电路分析相量法
量的相量乘以 jω ，即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ，辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ，其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i )，则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 ， F2 a2 jb2 ，则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则：
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1－F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明：
复指数函数实部的导数等于复指数函数导数的实部；
第八章相量法
i i
i
i
i
如 i 26 2 cos(t 60) A 26e j 60 A 2660 A I 对应的有效值相量为：
Im 26 2e j 60 A 26 260 A 其最大值相量为：
U 同理若有： 220e j 30V 则有; u 220 2 cos(t 30)V 2.相量图 相量是一个复数，它在复平面上的图形称为相量图。 若用旋转相量表示为，2Ie j e jt 其中复常数 2Ie j 2I i 称为旋转相量的复振幅， e jt 是一个随时间变化而以角速度不断逆时针旋转 的因子，两者的乘积即表示复振幅在复平面上不断 逆时针旋转，故称之为旋转相量，这就是复指数 函数的几何意义。
dt 2
③正弦量的积分
i 2I cos(t i ) 则 idt Re [ 2 Ie jt ]dt Re [ 2 Ie jt dt ] 如
jt I I Re [ 2 ( )e ] 2 cos(t i ) j 2
即正弦量的积分为同频率正弦量，其相量等于原 j 相量 I 除以 . I I 表示为： ( i ) idt
F F1 F2 F1 F2 [cos( 1 2 ) j sin(1 2 )]
F1 a1 jb1 (a1 jb1 )(a2 jb2 ) a1a2 b1b2 a2 b1 a1b2 j 2 2 2 2 F2 a2 jb2 (a2 jb2 )(a2 jb2 ) a2 b2 a2 b2
1
i1 I1m cos(t i 1 ) A 和 i2 I 2 m cos(t i 2 ) A 则 i1 与 i 2 如 的相位差 12 (t i1 ) (t i 2 ) i1 i 2 （初相之差）
i
i
i
如 i 26 2 cos(t 60) A 26e j 60 A 2660 A I 对应的有效值相量为：
Im 26 2e j 60 A 26 260 A 其最大值相量为：
U 同理若有： 220e j 30V 则有; u 220 2 cos(t 30)V 2.相量图 相量是一个复数，它在复平面上的图形称为相量图。 若用旋转相量表示为，2Ie j e jt 其中复常数 2Ie j 2I i 称为旋转相量的复振幅， e jt 是一个随时间变化而以角速度不断逆时针旋转 的因子，两者的乘积即表示复振幅在复平面上不断 逆时针旋转，故称之为旋转相量，这就是复指数 函数的几何意义。
dt 2
③正弦量的积分
i 2I cos(t i ) 则 idt Re [ 2 Ie jt ]dt Re [ 2 Ie jt dt ] 如
jt I I Re [ 2 ( )e ] 2 cos(t i ) j 2
即正弦量的积分为同频率正弦量，其相量等于原 j 相量 I 除以 . I I 表示为： ( i ) idt
F F1 F2 F1 F2 [cos( 1 2 ) j sin(1 2 )]
F1 a1 jb1 (a1 jb1 )(a2 jb2 ) a1a2 b1b2 a2 b1 a1b2 j 2 2 2 2 F2 a2 jb2 (a2 jb2 )(a2 jb2 ) a2 b2 a2 b2
1
i1 I1m cos(t i 1 ) A 和 i2 I 2 m cos(t i 2 ) A 则 i1 与 i 2 如 的相位差 12 (t i1 ) (t i 2 ) i1 i 2 （初相之差）
相量法
+j F1 0 F = F1 + F2 F2 +1
复数的乘除运算 a. 复数的乘除运算可以用代数形式进行 例如：设F1 =a1+jb1, F2 =a2+jb2, 则
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 - b1b2 ) j(a1b2 a2b1 )
F1 a1 jb1 (a1 jb1 )(a2 - jb2 ) F2 a2 jb2 (a2 jb2 )(a2 - jb2 )
a1a2 b1b2 a2b1 - a1b2 j 2 2 (a2 ) (b2 ) (a2 )2 (b2 )2
b. 复数的乘除运算也可以用指数形式和极坐标进行（方便）
两个复数的相乘，用指数形式进行, 有
F1F2 F1 e
用极坐标形式表示, 有
j1
F2 e
j 2
F1 F2 e
3. 相量图 相量图: 相量是一个复数，它在复平面上的图形称为相量图。
I i (t ) 2 Icos(ω t i ) I i
U u(t ) 2Ucos(t u ) U u
U
u
i
I
4. 正弦量运算转换为相应相量运算 (1) 同频率正弦量的代数和
2 倍的关系。
工程中一般说正弦电压、电流的大小都指有效值。如测量 仪表上的刻度，设备名牌上的额定电压、电流均指有效值。 但电器设备的绝缘水平 — 耐压值按最大值考虑。
§8. 3相量法的基础
1. 相量法的理论基础 从电路分析中常涉及到的计算看：有正弦量乘常数（欧姆定 律），正弦量的微分、积分（电感、电容电路的电压电流约 束关系），同频率正弦量的代数和（KCL和KVL）等运算， 其结果仍是一个同频率的正弦量。 在线性电路中，若激励是正弦量，则电路中各支路的电压和 电流的稳态响应将是同频率的正弦量；若电路中有多个同频 率激励源时，根据线性电路的叠加定理，则电路的全部稳态 响应都将是同频率的正弦量 — 这是一个基本的结果。 基于以上原因，在同频正弦量的电路计算中，ω是已知 的常 数，正弦量的三要素已退化成两个要素，有效值（最大值） 和初相，注意到一个复数（相量）也有两个要素：模和辐角， 这使得可用复数表征一个正弦量的信息（要素）。 电工技术中的非正弦周期函数，可以分解成频率为整数倍的 正弦函数的无穷级数，最终归结为这里讨论的正弦稳态分析。
复数的乘除运算 a. 复数的乘除运算可以用代数形式进行 例如：设F1 =a1+jb1, F2 =a2+jb2, 则
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 - b1b2 ) j(a1b2 a2b1 )
F1 a1 jb1 (a1 jb1 )(a2 - jb2 ) F2 a2 jb2 (a2 jb2 )(a2 - jb2 )
a1a2 b1b2 a2b1 - a1b2 j 2 2 (a2 ) (b2 ) (a2 )2 (b2 )2
b. 复数的乘除运算也可以用指数形式和极坐标进行（方便）
两个复数的相乘，用指数形式进行, 有
F1F2 F1 e
用极坐标形式表示, 有
j1
F2 e
j 2
F1 F2 e
3. 相量图 相量图: 相量是一个复数，它在复平面上的图形称为相量图。
I i (t ) 2 Icos(ω t i ) I i
U u(t ) 2Ucos(t u ) U u
U
u
i
I
4. 正弦量运算转换为相应相量运算 (1) 同频率正弦量的代数和
2 倍的关系。
工程中一般说正弦电压、电流的大小都指有效值。如测量 仪表上的刻度，设备名牌上的额定电压、电流均指有效值。 但电器设备的绝缘水平 — 耐压值按最大值考虑。
§8. 3相量法的基础
1. 相量法的理论基础 从电路分析中常涉及到的计算看：有正弦量乘常数（欧姆定 律），正弦量的微分、积分（电感、电容电路的电压电流约 束关系），同频率正弦量的代数和（KCL和KVL）等运算， 其结果仍是一个同频率的正弦量。 在线性电路中，若激励是正弦量，则电路中各支路的电压和 电流的稳态响应将是同频率的正弦量；若电路中有多个同频 率激励源时，根据线性电路的叠加定理，则电路的全部稳态 响应都将是同频率的正弦量 — 这是一个基本的结果。 基于以上原因，在同频正弦量的电路计算中，ω是已知 的常 数，正弦量的三要素已退化成两个要素，有效值（最大值） 和初相，注意到一个复数（相量）也有两个要素：模和辐角， 这使得可用复数表征一个正弦量的信息（要素）。 电工技术中的非正弦周期函数，可以分解成频率为整数倍的 正弦函数的无穷级数，最终归结为这里讨论的正弦稳态分析。
电路相量法
电路相量法相量法是分析讨论正弦电流电路稳定状态的一种简洁易行的方法。
它是在数学理论和电路理论的基础上建立起来的一种系统方法。
1、问题的提出在上图所示的电路中，依据KVL，列写微分方程如下当激励u(t)是正弦量时，uC(t)及iL(t)均为同频率的正弦量。
这一重要结论具有普遍意义，即线性非时变电路在正弦电源激励下，各支路电压、电流的特解都是与激励同频率的正弦量，当电路中存在有多个同频率的正弦激励时，该结论也成立。
工程上将电路的这一特解状态称为正弦电流电路的稳定状态，简称正弦稳态。
电路处于正弦稳态时，同频率的各正弦量之间仅在有效值（或幅值）、初相上存在差异和联系，这种"差异和联系"正是正弦稳态分析求解中的关键问题。
结论：同频的正弦量相加仍得到同频的正弦量，所以，只需确定初相位和有效值。
因此采纳2、正弦量的相量表示：构造一个复函数，（无任何物理意义）取该复函数的实部，，为一个正弦量，有物理意义。
结论：任意一个正弦时间函数都有唯一与其对应的复数函数。
如复函数F(t) 还可以写成，其中为复常数。
F(t) 包含了正弦量的三要素：幅值（此处为有效值）I、初相Y 、角频率w。
有如下关系同样可以建立正弦电压与相量的对应关系：正弦量除可用上述的相量式表示以外，还可在复平面上用相量图形式表示。
如图所示。
图相量图留意相量的模表示正弦量的有效值；相量的辐角表示正弦量的初相位。
例已知，试用相量表示i和u。
解：3、相量法的应用① 同频率正弦量的加减所以相量关系为：结论：同频正弦量的加减运算变为对应相量的加减运算。
同频率的正弦量相加减，还可以借助相量图进行计算。
令，，下面用相量图求解。
图(a)为平行四边形法则求解，图(b)为三角形法则求解。
(a) (b)图相量图进行相量的加法运算② 正弦量的微分、积分运算令微分运算：积分运算：所以；相量法的优点：① 把时域问题变为复数问题；② 把微积分方程的运算变为复数方程运算；③ 可以把直流电路的分析方法直接用于沟通电路。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i , Im , I
例:i = 10 sin(314t+30°) A ° u= 5 cos(314t-150°) V ° 求电压和电流的相位差. 求电压和电流的相位差.
= 30° (150°) = 180°
i = 10 sin(314t+30°) ° = 10 cos(314t+30°-90°) ° ° = 10 cos(314t-60°) °
i 2,角频率ω ,角频率 Im 反映正弦量变化的快慢 2π 单位 rad/s O ωT=2π,ω=2πf π f=1/T ψi 频率f 的单位为赫兹 赫兹( ) 频率 的单位为赫兹(Hz) 周期T的单位为 的单位为秒 ) 周期 的单位为秒(s) f =50Hz,T = 0.02s ω =314 rad/s
二,正弦量的三要素: 正弦量的三要素
i + 瞬时值表达式: 瞬时值表达式: u
振幅I 角频率 初相位(角 角频率ω,初相位 振幅 m,角频率 初相位 角)ψi
-
i = I m cos( ω t + ψ i )
1,振幅Im ,振幅 正弦量在整个振荡过程中达到的最大值. 正弦量在整个振荡过程中达到的最大值.
i = 10 sin(314t+30°) °
= 60° (150°) = 90°
两个正弦量进行相位比较时应满足同频率,同函数,同符 两个正弦量进行相位比较时应满足同频率,同函数, 计算下列两正弦量的相位差. 计算下列两正弦量的相位差. 解 例 且在主值范围比较. 号,且在主值范围比较.
(1) i1(t ) = 10cos(100π t + 3π 4) i2 (t ) = 10cos(100π t π 2)
U=
def
1 T
∫
T
0
u ( t )dt
2
设
1 T 2 2 i(t)=Imcos(ω t+Ψ ), I = ∫0 Im cos ( ω t +Ψ ) dt T
∵
∫
T
0
cos ( ω t +Ψ ) dt = ∫
2
T
0
1+ cos 2(ω t +Ψ ) 1 dt = t 2 2
T 0
1 = T 2
1 2 T Im Im = ∴ I= = 0.707Im T 2 2
0
一,正弦稳态电路
§8.3 相量法的基础 8.3
在线性电路中,如果激励是正弦量, 在线性电路中,如果激励是正弦量,则电路中 各支路的电压和电流的稳态响应将是同频正弦量. 同频正弦量 各支路的电压和电流的稳态响应将是同频正弦量. 如果电路有多个激励且都是同一频率的正弦量, 如果电路有多个激励且都是同一频率的正弦量, 多个激励且都是同一频率的正弦量 则根据线性电路的叠加性质, 则根据线性电路的叠加性质,电路全部稳态响应都 将是同一频率的正弦量. 同一频率的正弦量 将是同一频率的正弦量. 处于这种稳定状态的电路称为正弦稳态电路, 处于这种稳定状态的电路称为正弦稳态电路, 正弦稳态电路 又可称正弦电流电路 正弦电流电路. 又可称正弦电流电路.
1 1
1
F2 =| F2 | ∠θ 2
F1 F 2 = F1 ∠ θ 1 F 2 ∠ θ 2
4,除法 ,
= F1 F 2 / θ 1 + θ 2
F1 = F2
| F1 | ∠θ1
| F2 | ∠θ 2
=
F1 F2
/θ1 θ 2
三,旋转因子
e
jθ
e
jθ
= 1/θ
是一个模等于1,辐角为 的复数 的复数. 是一个模等于 ,辐角为θ的复数. 任意复数A乘以 任意复数 乘以e jθ 乘以
3 +/a 4 5 辐角 模 b a 126.869897 5 注意选择角度DEG 注意选择角度 b
2nd
→rθ
计算器上的复数运算操作
极坐标形式→代数式 极坐标形பைடு நூலகம் 代数式
10 /60° = 5 + j8.66 °
1 0 a 6 0 5 虚部 实部 b a 8.6602540 5
注意选择角度DEG 注意选择角度 b
b
+j F
θ
O a
+1
2,三角形式 ,
+j b F
F = F (cos θ + j sin θ )
θ
O a
模
+1
F =
a +b
2
2
辐角
b θ = arctan a
3,指数形式 ,
根据欧拉公式
e = cosθ + j sin θ e = cosθ j sin θ
jθ jθ
F = F (cos θ + j sin θ )
(2) i1(t ) = 10cos(100π t + 300 ) i2 (t ) = 10sin(100π t 150 ) (3) u1(t ) = 10cos(100π t + 300 ) u2 (t ) = 10cos(200π t + 450 )
= 3π 4 (π 2) = 5π 4 > 0 = 2π 5π 4 = 3π 4
2nd
→xy
二,复数的运算
1,加法 , 代数形式进行 进行,设 用代数形式进行 设 F1 = a1 + jb1
F2 = a2 + jb2 F1 + F2 = ( a1 + jb1 ) + ( a2 + jb2 )
= (a1 + a2 ) + j(b1 + b2 )
几何意义 +j
F + F2 1
F1
例如 一个复数乘以 , 一个复数乘以j, 乘以
e
j
π
2
= j, e
j
π
2
= -j, e jπ = -1
等于把该复数逆时针旋转π/2, 等于把该复数逆时针旋转 , 一个复数除以 , 一个复数除以j, 除以 等于把该复数乘以-j, 等于把该复数乘以-j, 等于把它顺时针旋转π/2 . 等于把它顺时针旋转 虚轴等于把实轴+1乘以 而得到的 虚轴等于把实轴 乘以j而得到的. 乘以 而得到的.
第八章 相量法
§8.1 复数 8.1 §8.2 正弦量 8.2 §8.3 相量法的基础 8.3 §8.4 电路定律的相量形式 8.4
§8.1 复数 8.1
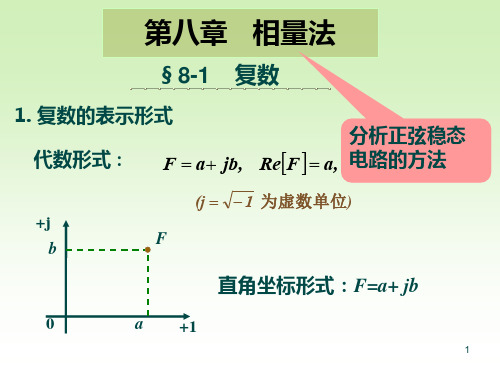
一,复数的形式
1,代数形式 ,
j= 1
F = a + jb
为虚单位 复数F 复数 的实部 Re[F ] = a 复数F 复数F 的虚部 Im[F ] = b 复数 F 在复平面上可以用一条从 原点O 指向F 对应坐标点的有向 原点 指向 对应坐标点的有向 线段表示 表示. 线段表示.
2 Ie
jψ i
e
j t
Im = 2I
i(t ) = Im cos(ω t +Ψ ) = 2I cos(ω t +Ψ )
同理,可得正弦电压有效值与最大值的关系: 同理,可得正弦电压有效值与最大值的关系:
U=
1 2
Um
或
Um = 2U
若一交流电压有效值为U=220V,则其最大值为Um≈311V; ,则其最大值为 若一交流电压有效值为 ; U=380V, Um≈537V. , . 工程上说的正弦电压,电流一般指有效值, 注 (1)工程上说的正弦电压,电流一般指有效值,如设 备铭牌额定值, 电网的电压等级等. 但绝缘水平, 备铭牌额定值 , 电网的电压等级等 . 但绝缘水平 , 耐压值 指的是最大值.因此, 指的是最大值 . 因此 , 在考虑电器设备的耐压水平时应按 最大值考虑. 最大值考虑. (2)测量中,交流测量仪表指示的电压,电流读数一 测量中,交流测量仪表指示的电压, 般为有效值. 般为有效值. (3)区分电压,电流的瞬时值,最大值,有效值的符号. 区分电压,电流的瞬时值,最大值,有效值的符号.
显然有 Re[ F] = F cos(ωt +ψ) 所以正弦量可以用上述形式的复指数函数描述, 复指数函数描述 所以正弦量可以用上述形式的复指数函数描述, 使正弦量与其实部一一对应起来. 使正弦量与其实部一一对应起来. 如以正弦电流 i = 2 I cos( ω t + ψ i ) 为例
i = Re[
2π
ωt
3,初相位(角)ψi ,初相位( 主值范围内取值 主值范围内取值
i Im 2π O
ψi ≤180°
ψi
π
2π
ωt
(ω t + ψ i ) 称为正弦量的相位,或称相角. 称为正弦量的相位,或称相角.
d (ω t + ψ i ) ω = dt
三,正弦量的有效值
周期性电流,电压的瞬时值随时间而变, 周期性电流,电压的瞬时值随时间而变,为了衡量其 平均效果工程上采用有效值来表示. 平均效果工程上采用有效值来表示. 周期电流,电压有效值 周期电流,电压有效值(effective value)定义 定义
i2 (t ) = 10cos(100πt 1050 )
= 300 (1050 ) = 1350
ω1 ≠ ω2
不能比较相位差
(4) i1(t ) = 5cos(100π t 30 )
0
i2 (t ) = 3cos(100πt 1500 )
= 300 (1500 ) = 1200
i2 (t ) = 3cos(100π t + 30 )
?
π
2
等于把复数A逆时针旋转一个角度θ, 等于把复数 逆时针旋转一个角度 , 逆时针旋转一个角度 的模值不变. 而A的模值不变. 的模值不变
e
j