道路施工测量竖曲线的测设

兰州资源环境职业技术学院教师授课教案【相关知识】五、圆曲线放样无论是铁路、公路还是地铁隧道和轻轨，由于受到地形、地物、地质及其他因素的限制，经常要改变线路前进的方向。

当线路方向改变时，在转向出需要用曲线将两直线连接起来。

因此，线路工程总是有直线和曲线所组成，如图2-16(a)所示。

曲线按其线形可分为：圆曲线、缓和曲线、复曲线和竖曲线等。

道路曲线分为平面曲线(平曲线)和立面曲线(竖曲线)。

连接不同方向线路的曲线称为平曲线；当相邻两段直线段存在坡度时，也必须用曲线连接，这种连接不同坡度的曲线称为竖曲线。

平曲线按其线形可分为圆曲线、缓和曲线、综合曲线等。

圆曲线又分为单曲线和复曲线两种：具有单一曲率半径的曲线称为单曲线；具有两个或两个以上不同曲率半径的曲线称为复曲线，如图2-16(b)所示。

（a ）线路曲线(b)复曲线 (c)回头曲线 图2-16 线路曲线图在一般情况下，为了保证车辆运输的安全与平顺，都要在直线与圆曲线之间设置缓和曲线。

缓和曲线的曲率半径是从∞逐渐过渡到圆曲线半径R 的。

在与直线连接处的半径为∞,与圆曲线连接处的半径为R 。

铁路线路及厂区内的线路除联络线外均采用圆曲线；国等级铁路和厂区外的专用铁路线路，当曲线半径超过一定的数值时，也可以只采角圆曲在公路线路上，2JD公里数前加注“K ”。

曲线上各点的里程都是从一已知里程的点开始沿曲线逐点推算的。

一般已知交点JD 的里程是从前一直线段推算而得，然后再由交点的里程推算出其他各主点的里程。

由于路线中线不经过交点，所以圆曲线的终点、中点的里程必须从圆曲线起点的里程沿着曲线长度推算。

根据交点的里程和曲线放样元素，就能够计算出个主点的里程，如图2-17所示。

图 2-17 圆曲线示意图⎪⎪⎪⎭⎪⎪⎪⎬⎫+==+==)(2qDK QZ DK 2L-DK YZ DK QZ L DK ZY DK YZ T -DK JD DK 校核JD ZY (2-2) 例2-1 已知某交点的里程为DK4+542.36m ，测得偏角"'︒=362530右α，圆曲线的半径R=150m ，求圆曲线的元素和主点里程。

浙江广厦建设职业技术学院20 /20 学年第一学期所属分院课程名称授课教师教研室主任课题：第九章道路工程测量第三讲道路工程施工测量课型：讲授教学目的与要求：1．了解道路施工测量含义及任务。

2．理解路线中线的恢复；竖曲线测设数据的计算。

3．掌握施工控制桩的测设；路基边桩的测设。

教学重点、难点：重点：路线中线的恢复；竖曲线测设数据的计算；施工控制桩的测设；路基边桩的测设。

难点：路基边桩的测设；竖曲线测设数据的计算。

采用教具、挂图：多媒体课件复习、提问：1．道路施工测量的主要任务包括哪些？2．施工控制桩的测设方法及各自的适用条件？3．路基边桩的测设方法及各自的适用条件？4．路基边坡的测设的步骤？5．竖曲线设置的位置及目的？课堂小结：本次课主要学习了道路工程施工测量，应使学生重点掌握路线中线的恢复；竖曲线测设数据的计算；施工控制桩的测设；路基边桩的测设。

作业：8课后分析：第四节道路工程施工测量道路施工测量就是利用测量仪器和设备，按照设计图纸中的各项元素（如道路平、纵、横元素），依据控制点或路线上的控制桩的位置，将道路的“样子”具体地标定在实地，以指导施工作业。

道路施工测量的主要任务包括：恢复中线测量、施工控制桩测设、路基边桩和边坡测设、竖曲线测设等。

一、路线中线的恢复道路勘测完成到开始施工这一段时间内，有一部分中线桩可能被碰或丢失，因此施工前应进行复核并进行恢复。

在恢复中桩时，应将道路附属物，如涵洞、检查井和挡土墙的位置一并确定。

对于部分改线地段，应重新定线，并绘制相应的纵横断面图。

二、施工控制桩的测设因中线桩在路基施工中都要被挖掉或堆埋，为了在施工中能控制中线位置，应不易受施工干扰，便于引用、易于保存桩位的地方测设施工控制桩，测设方法如下：1、平行线法平行线法是在路基以外测设两排平行于中线的施工控制桩，如图9-22所示，此法多用于地势平坦、直线段较长的线路图9-222、延长线法延长线法是在道路转弯处的中线延长线上或者在曲线中点至交点连线的延长线上，测设两个能够控制交点位置的施工控制桩，如图9-23所示。

1.某山岭区一般二级公路，变坡点桩号为K5＋030，高程为427.68m ，%51=i ，%42-=i ，竖曲线半径R ＝2000m 。

试计算竖曲线各要素以及桩号为k5＋000和K5＋100处的设计高程。

解：⑴计算竖曲线要素09.005.004.012-=--=-=i i ω，为凸形竖曲线。

曲线长20000.09180L R m ω==⨯=切线长m L T 9021802=== 外距2290 2.03222000T E m R ===⨯ ⑵计算设计高程竖曲线起点桩号＝（K5+30）－90=K4+940竖曲线起点高程＝427.68－90×0.05＝423.18m桩号K5+000处：横距m K K x 60)9404()0005(1=+-+= 竖距m R x h 9.040006022211=== 切线高程＝423.18＋60×0.5＝426.18m设计高程＝426.18－0.9＝425.28m桩号K5＋100处：横距m K K x 160)9404()1005(2=+-+= 竖距m R x h 4.6400016022222=== 切线高程＝423.18＋160×0.05＝431.18m设计高程＝431.18－6.4＝424.78m2．某山岭区二级公路，已知JD1、JD2、JD3的坐标分别为（40961.914,91066.103）、（40433.528,91250.097）、（40547.416,91810.392），并设JD2的R=150m ，Ls=40m ，求JD2的曲线要素。

解：⑴计算出JD2、JD3形成的方位角fwj2，︒=--=48966.11528.40433416.40547097.91250392.91810arctan 2fwj 计算出JD1、JD2形成的方位角fwj1， ︒=--=19908.289914.40961528.40433103.91066097.91250arctan1fwj 曲线的转角为α＝360＋fwj2－fwj1＝82.29058°⑵由曲线的转角，计算出曲线的切线长T ，曲线长L 及超距J3322402019.9882240240150s s L L q R =-=-=⨯ 24243340400.444242384241502384150s s L L p R R =-=-=⨯⨯ ︒===639.7150406479.286479.280R L s β 438.151988.19229058.82tan )444.0150(2tan )(=++=++=q p R T α 0150(2)2(82.2905827.639)240290.526180180s RL L ππαβ⨯=-+=-⨯+⨯= 781.49150229058.82sec )444.0150(2sec )(=-+=-+=R p R E α下面总结范文为赠送的资料不需要的朋友，下载后可以编辑删除！祝各位朋友生活愉快！员工年终工作总结【范文一】201x年就快结束，回首201x年的工作，有硕果累累的喜悦，有与同事协同攻关的艰辛，也有遇到困难和挫折时惆怅，时光过得飞快，不知不觉中，充满希望的201x年就伴随着新年伊始即将临近。

道路施工测量竖曲线测设在路线纵坡改变处, 考虑到行车视距要求和行车平稳, 在竖直面内应用曲线衔接起来, 这种曲线称为竖曲线, 如图所表示, 路线上有3条相邻纵坡1i , 2i , 3i , 在1i 和2i 之间设置凸形竖曲线, 在2i 和3i 之间设置凹形竖曲线。

竖曲线通常采取较简单圆曲线, 这是因为在通常情况下, 相邻坡度差都较小, 而选择竖直线半径又较大, 所以采取其她复杂曲线所得到结果, 基础上与圆曲线相同。

如图所表示, 两相邻纵坡坡度分别为1i , 2i , 则竖曲线坡度转角α为: 21arctan arctan i i -=α因为α角很小, 上式可简化为:21i i -=α。

考虑到竖曲线半径R 较大, 而转角α又较小, 故竖曲线测设元素也能够按下列近似公式求得:又因α很小, 故可认为y 坐标轴与半径方向一致, 也认为它是曲线上点与切线上对应点高程差, 由上图不难得到:()222x R y R +=+即222y x Ry -=因2y 与2x 相比, 其值甚微, 可略去不计, 故有22xRy =, 求得高程差y 以后, 即可按下式计算竖曲线任一点P 高程p H :p p y H H ±=式中 H ——该点在切线上高程, 也就是坡道线高程;p y ——该点高程更正, 当竖曲线为凸形曲线时, p y 为负; 反之为正。

例: 设某竖曲线半径R=5000m, 相邻坡段坡度%114.11-=i , %154.02+=i , 为凹形竖曲线, 变坡点桩号为K1+670, 高程为48.60m, 假如曲线上每个10设置一桩, 试计算竖曲线上各点高程。

解: 计算竖曲线元素, 可求得:m m i i R T 7.31%154.0%114.15000212121=--⨯⨯=-=4.63%154.0%114.1500021=--⨯=-=m i i R L()m m m R T E 10.0500027.31222=⨯== 起点桩号=K1+（670-31.7）=K1+638.30终点桩号=K1+（638.3+63.4）=K1+701.70起点高程=48.6m+31.7m*1.114%=48.95m终点高程=48.6m+31.7m*0.154%=48.65m按R=5000m 和对应桩距, 即可求得竖曲线上各桩高程更正数i y , 计算结果见表。

施工测量一、道路施工测量道路施工测量主要包括恢复路线中线、路基边桩的测设、竖曲线的测设等项工作。

（一）、路线中线的恢复从路线勘测到开始施工这段时间里，往往会有一些中桩丢失，故在施工之前，应根据设计文件进行恢复工作，并对原来的中线进行复核，以保证路线中线位置准确可靠。

恢复中线所采用的测量方法与路线中线测量方法基本相同。

此外，对路线水准点也应该进行复核，必要时还应增设一些水准点以满足施工需要。

（二）、路基边桩的测设路基边桩测设就是在地面上将每一个横断面的路基边坡线与地面的交点用木桩标定出来。

边桩的位置由两侧边桩至中线的距离来确定。

常用的变桩测设方法如下。

1.图解法直接在横断面图上量取中桩至边桩的距离，然后在实地用皮尺沿横断面方向测定具体位置。

当挖填方不很大时，采用此法较简单。

2.解析法路基边桩至中桩的平距系通过计算求得。

（1）平坦地段路基边桩的测设：填方路基称为路堤。

如图12-1所示，路基边桩至中桩的距离为D=B/2+mh （12-1）挖方路基称为路堑。

如图12-2所示，路堑边桩至中桩的距离为D=B/2+S+mh （12-2）以上两式中：B—路基设计宽度；1：m—路基边坡坡度H—填土高度或挖土深度S—路堑边沟顶宽。

以上是断面位于直线段时计算D值的方法。

若断面位于曲线上有加宽时，在以上述方法求出D值后，还应于曲线内侧的D值中加上加宽值。

（2）倾斜地段路基边桩的测设，在倾斜地段，边桩至中桩的距离随着地面坡度的变化而变化。

如图12-3所示，路基边桩至中桩的距离为斜坡上侧D上=B/2+m（h中–h上）斜坡下侧D下=B/2+m（h中+h下）（12-3）如图12-4所示，路堑边桩至中桩的距离为斜坡上侧D上=B/2+S+m（h中+h上）斜坡下侧D下=B/2+S+m（h中- h下）（12-4）式中，B、S和m为已知，h中为中桩处的填挖高度，亦为已知。

h上、h下为斜坡上、下侧边桩与中桩的高差，在边桩未定出之前则为未知数。

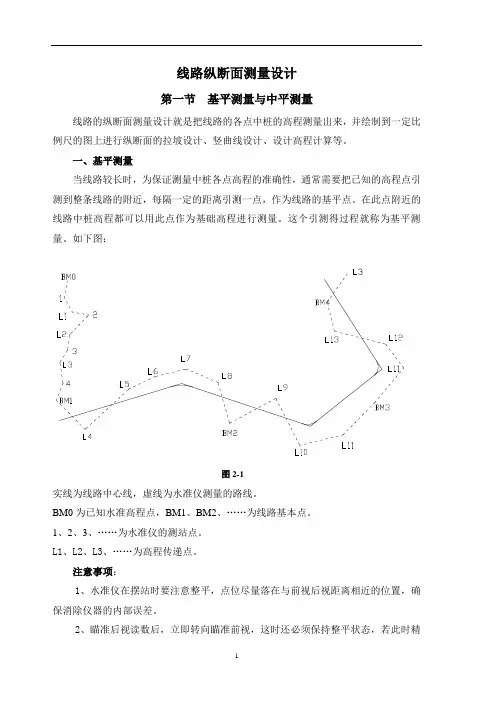
线路纵断面测量设计第一节基平测量与中平测量线路的纵断面测量设计就是把线路的各点中桩的高程测量出来，并绘制到一定比例尺的图上进行纵断面的拉坡设计、竖曲线设计、设计高程计算等。

一、基平测量当线路较长时，为保证测量中桩各点高程的准确性，通常需要把已知的高程点引测到整条线路的附近，每隔一定的距离引测一点，作为线路的基平点。

在此点附近的线路中桩高程都可以用此点作为基础高程进行测量。

这个引测得过程就称为基平测量。

如下图：图2-1实线为线路中心线，虚线为水准仪测量的路线。

BM0为已知水准高程点，BM1、BM2、……为线路基本点。

1、2、3、……为水准仪的测站点。

L1、L2、L3、……为高程传递点。

注意事项：1、水准仪在摆站时要注意整平，点位尽量落在与前视后视距离相近的位置，确保消除仪器的内部误差。

2、瞄准后视读数后，立即转向瞄准前视，这时还必须保持整平状态，若此时精平水准泡错开，则瞄准前视后，还必须在此状态下进行精平，然后再读数。

3、为确保测量的准确性，要求往返测量，精度在普通测量学的要求以内，读数方可使用。

也可以用双面尺的方法进行校核，在测量中尽量每站进行校核。

4、基平测量的数据应进行平差处理后方可使用。

具体平差方法见普通测量知识。

5、测量时，水准尺应该垂直，读数时应首先消除视差，司仪者读中丝卡位的最小数据，以保证读数最准确。

6、立尺的测量员必须保证尺的底端不带泥土，用塔尺时要注意尺间不脱节。

二、中平测量中平测量就是在基平测量的基础上，基平时引测的高程点作为基准高程，用水准仪测出每个中桩的地面高程，又称中桩抄平。

图2-2三、记录记录时应该注意的是要保证填写准确，判断哪些是前视，哪些是中视，哪些是后视。

传递高程的点应该既有前视也有后视，只有中视的点没有传递高程。

例题：按下图填写表格，并计算高程，1点高程100.00。

图2-3表2-1第二节拉坡设计拉坡设计就是在中平测量的基础上，利用中平测量的每个中桩高程的数据进行地面线的设计，由此计算各中桩的设计高程。