BP神经网络拟合函数
- 格式:doc
- 大小:469.50 KB
- 文档页数:13




基于BP神经网络的非线性函数拟合——程序设计说明程序设计说明:1.确定网络结构首先,需要确定BP神经网络的结构,包括输入层、隐藏层和输出层的节点数。
输入层的节点数由样本的特征数确定,隐藏层的节点数可以通过试验确定,输出层的节点数则由问题的要求确定。
2.初始化网络参数初始化网络的权值和偏置,可以使用随机数生成,初始值不能太大或太小。
权值和偏置的初始值会对模型的训练效果产生影响,一般可以根据问题的复杂程度来选择。
3.前向传播通过前向传播,将样本数据输入到神经网络中,并计算每个神经元的激活值。
激活函数可以选择Sigmoid函数或者ReLU函数等非线性函数。
4.计算误差5.反向传播通过反向传播,将误差从输出层向输入层传播,更新网络的权值和偏置。
反向传播的过程可以使用梯度下降法来更新网络参数。
6.训练网络7.测试网络使用未参与训练的样本数据测试网络的泛化能力,计算测试误差。
如果测试误差较小,说明网络能够较好地拟合非线性函数。
8.参数调优根据训练误差和测试误差结果,可以调整网络的参数,如学习率、隐藏层节点数等,以提高网络的训练效果和泛化能力。
9.反复训练和测试网络根据需要,反复进行训练和测试的过程,直至网络的训练误差和测试误差均满足要求。
这是一个基于BP神经网络的非线性函数拟合的程序设计说明,通过实现以上步骤,可以有效地进行非线性函数的拟合和预测。
在具体实现中,可以使用Python等编程语言和相应的神经网络框架,如TensorFlow、PyTorch等,来简化程序的编写和调试过程。
同时,为了提高程序的性能和效率,可以使用并行计算和GPU加速等技术。

BP 神经网络与多项式拟合曲线摘要 首先介绍了曲线拟合的原理及其在曲线拟合中的应用。
接着讨论了BP 神经网络的原理,研究了非线性拟合的在MATLAB 中仿真过程 通过比较可以看出利用神经网络进行非线性拟合具有拟合速度快、拟合精度高的特点。
关键词:曲线拟合;BP 神经网络;MATLAB0 引言在实际工程应用和科学实践中,为了描述不同变量之间的关系,需要根据一组测定的数据去求得自变量x 和因变量y 的一个函数关系)(x f y =,使其在某种准则下最佳地接近已知数据。
曲线拟合是用连续曲线近似地刻画或比拟平面上离散点组所表示坐标之间的函数关系的一种数据处理方法。
从一组实验数据(i i y x ,) 中寻求自变量x 和因变量y 之间的函数关系)(x f y =来反映x 和y 之间的依赖关系,即在一定意义下最佳地逼近已知数据。
应用曲线拟合的方法揭示数据之间内在规律具有重要的理论和现实意义。
1 多项式曲线拟合 1.1 曲线拟合原理最小二乘法原理:对给定的数据点(i i y x ,)(N i ,...,2,1=),在取定的函数类φ中,求函数φ∈)(x f ,使误差i i y x f -)((N i ,...,1,0=)的平方和最小,即[]∑=-Ni iiy x f 02)(取到最小值。
从几何意义上讲,就是寻求与给定点(i i y x ,)(N i ,...,2,1=)的距离平方和为最小的曲线)(x f y =。
函数)(x f 称为拟合函数或最小二乘解,求拟合函数)(x f 的方法称为曲线拟合的最小二乘法。
拟合函数和标志数据点之间的垂直距离是该点的误差。
对该数据点垂直距离求平方,并把平方距离全加起来,拟合曲线应是使误差平方和尽可能小的曲线,即是最佳拟合。
1.2 最小二乘法曲线拟合对非线性函数)+=,进行曲线拟合。
xy-16ex p(22x1.2.1 拟合过程选取拟合区间为-5:0.1:5.用10阶、30阶不同阶数对函数进行拟合,绘制出拟合曲线图,比对拟合效果差异。

BP神经网络用于函数拟合与模式识别的Matlab示例程序clcclearclose all%---------------------------------------------------% 产生训练样本与测试样本,每一列为一个样本P1 = [rand(3,5),rand(3,5)+1,rand(3,5)+2];T1 = [repmat([1;0;0],1,5),repmat([0;1;0],1,5),repmat([0;0;1],1,5)];P2 = [rand(3,5),rand(3,5)+1,rand(3,5)+2];T2 = [repmat([1;0;0],1,5),repmat([0;1;0],1,5),repmat([0;0;1],1,5)];%---------------------------------------------------% 归一化[PN1,minp,maxp] = premnmx(P1);PN2 = tramnmx(P2,minp,maxp);%---------------------------------------------------% 设置网络参数NodeNum = 10; % 隐层节点数TypeNum = 3; % 输出维数TF1 = 'tansig';TF2 = 'purelin'; % 判别函数(缺省值)%TF1 = 'tansig';TF2 = 'logsig';%TF1 = 'logsig';TF2 = 'purelin';%TF1 = 'tansig';TF2 = 'tansig';%TF1 = 'logsig';TF2 = 'logsig';%TF1 = 'purelin';TF2 = 'purelin';net = newff(minmax(PN1),[NodeNum TypeNum],{TF1 TF2});%---------------------------------------------------% 指定训练参数% net.trainFcn = 'traingd'; % 梯度下降算法% net.trainFcn = 'traingdm'; % 动量梯度下降算法%% net.trainFcn = 'traingda'; % 变学习率梯度下降算法% net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法%% (大型网络的首选算法 - 模式识别)% net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小%% 共轭梯度算法% net.trainFcn = 'traincgf'; % Fletcher-Reeves修正算法% net.trainFcn = 'traincgp'; % Polak-Ribiere修正算法,内存需求比Fletcher-Reeves 修正算法略大% net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大% (大型网络的首选算法 - 函数拟合,模式识别)% net.trainFcn = 'trainscg'; % Scaled Conjugate Gradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多%% net.trainFcn = 'trainbfg'; % Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快% net.trainFcn = 'trainoss'; % One Step Secant Algorithm,计算量和内存需求均比BFGS 算法小,比共轭梯度算法略大%% (中小型网络的首选算法 - 函数拟合,模式识别)net.trainFcn = 'trainlm'; % Levenberg-Marquardt算法,内存需求最大,收敛速度最快%% net.trainFcn = 'trainbr'; % 贝叶斯正则化算法%% 有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss', 'trainlm' %---------------------%net.trainParam.show = 1; % 训练显示间隔net.trainParam.lr = 0.3; % 学习步长 - traingd,traingdmnet.trainParam.mc = 0.95; % 动量项系数 - traingdm,traingdxnet.trainParam.mem_reduc = 10; % 分块计算Hessian矩阵(仅对Levenberg-Marquardt 算法有效)net.trainParam.epochs = 1000; % 最大训练次数net.trainParam.goal = 1e-8; % 最小均方误差net.trainParam.min_grad = 1e-20; % 最小梯度net.trainParam.time = inf; % 最大训练时间%---------------------------------------------------% 训练与测试net = train(net,PN1,T1); % 训练%---------------------------------------------------% 测试Y1 = sim(net,PN1); % 训练样本实际输出Y2 = sim(net,PN2); % 测试样本实际输出Y1 = full(compet(Y1)); % 竞争输出Y2 = full(compet(Y2));%---------------------------------------------------% 结果统计Result = ~sum(abs(T1-Y1)) % 正确分类显示为1Percent1 = sum(Result)/length(Result) % 训练样本正确分类率Result = ~sum(abs(T2-Y2)) % 正确分类显示为1Percent2 = sum(Result)/length(Result) % 测试样本正确分类率******************************************************************% BP 神经网络用于函数拟合% 使用平台 - Matlab6.5% 作者:陆振波,海军工程大学% 欢迎同行来信交流与合作,更多文章与程序下载请访问我的个人主页% 电子邮件:luzhenbo@% 个人主页:clcclearclose all%---------------------------------------------------% 产生训练样本与测试样本P1 = 1:2:200; % 训练样本,每一列为一个样本T1 = sin(P1*0.1); % 训练目标P2 = 2:2:200; % 测试样本,每一列为一个样本T2 = sin(P2*0.1); % 测试目标%---------------------------------------------------% 归一化[PN1,minp,maxp,TN1,mint,maxt] = premnmx(P1,T1);PN2 = tramnmx(P2,minp,maxp);TN2 = tramnmx(T2,mint,maxt);%---------------------------------------------------% 设置网络参数NodeNum = 20; % 隐层节点数TypeNum = 1; % 输出维数TF1 = 'tansig';TF2 = 'purelin'; % 判别函数(缺省值)%TF1 = 'tansig';TF2 = 'logsig';%TF1 = 'logsig';TF2 = 'purelin';%TF1 = 'tansig';TF2 = 'tansig';%TF1 = 'logsig';TF2 = 'logsig';%TF1 = 'purelin';TF2 = 'purelin';net = newff(minmax(PN1),[NodeNum TypeNum],{TF1 TF2});%---------------------------------------------------% 指定训练参数% net.trainFcn = 'traingd'; % 梯度下降算法% net.trainFcn = 'traingdm'; % 动量梯度下降算法%% net.trainFcn = 'traingda'; % 变学习率梯度下降算法% net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法%% (大型网络的首选算法)% net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小%% 共轭梯度算法% net.trainFcn = 'traincgf'; % Fletcher-Reeves修正算法% net.trainFcn = 'traincgp'; % Polak-Ribiere修正算法,内存需求比Fletcher-Reeves 修正算法略大% net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大% (大型网络的首选算法)%net.trainFcn = 'trainscg'; % Scaled Conjugate Gradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多%% net.trainFcn = 'trainbfg'; % Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快% net.trainFcn = 'trainoss'; % One Step Secant Algorithm,计算量和内存需求均比BFGS 算法小,比共轭梯度算法略大%% (中型网络的首选算法)net.trainFcn = 'trainlm'; % Levenberg-Marquardt算法,内存需求最大,收敛速度最快%% net.trainFcn = 'trainbr'; % 贝叶斯正则化算法%% 有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss', 'trainlm' %---------------------%net.trainParam.show = 20; % 训练显示间隔net.trainParam.lr = 0.3; % 学习步长 - traingd,traingdmnet.trainParam.mc = 0.95; % 动量项系数 - traingdm,traingdxnet.trainParam.mem_reduc = 1; % 分块计算Hessian矩阵(仅对Levenberg-Marquardt算法有效)net.trainParam.epochs = 1000; % 最大训练次数net.trainParam.goal = 1e-8; % 最小均方误差net.trainParam.min_grad = 1e-20; % 最小梯度net.trainParam.time = inf; % 最大训练时间%---------------------------------------------------% 训练net = train(net,PN1,TN1); % 训练%---------------------------------------------------% 测试YN1 = sim(net,PN1); % 训练样本实际输出YN2 = sim(net,PN2); % 测试样本实际输出MSE1 = mean((TN1-YN1).^2) % 训练均方误差MSE2 = mean((TN2-YN2).^2) % 测试均方误差%---------------------------------------------------% 反归一化Y2 = postmnmx(YN2,mint,maxt);%---------------------------------------------------% 结果作图plot(1:length(T2),T2,'r+:',1:length(Y2),Y2,'bo:')title('+为真实值,o为预测值')%输入样本点及其相应的类别,其中有一个奇异点P=[-0.5 -0.5 0.3 -0.1 0.2 0.0 0.6 0.8 60;-0.5 0.5 -0.5 1.0 0.5 -0.9 0.8 -0.6 20];T=[1 1 0 1 1 0 1 0 1];%在坐标图上绘出样本点plotpv(P,T);%建立一个感知器网络figure;plotpv(P,T);net=newp([-1 60;1 20],1);handle=plotpc(net.iw{1},net.b{1});%利用样本点训练网络并绘出得到的分类线E=1;while (sse(E)),[net,Y,E]=adapt(net,P,T);handle=plotpc(net.iw{1},net.b{1},handle);end;%局部放大分类线图figure;plotpv(P,T);plotpc(net.iw{1},net.b{1});axis([-2 2 -2 2]);%选择10个点来测试网络testpoints=[-0.5 0.3 -0.9 0.4 -0.1 0.2 -0.6 0.8 0.1 -0.4; -0.3 -0.8 -0.4 -0.7 0.4 -0.6 0.1 -0.5 -0.5 0.3]; a=sim(net,testpoints);%在坐标图上绘出网络的分类结果及分类线figure;plotpv(testpoints,a);plotpc(net.iw{1},net.b{1});%产生指定类别的样本点,并在图中绘出X = [0 1; 0 1]; % 限制类中心的范围clusters = 5; % 指定类别数目points = 10; % 指定每一类的点的数目std_dev = 0.05; % 每一类的标准差P = nngenc(X,clusters,points,std_dev);plot(P(1,:),P(2,:),'+r');title('输入样本向量');xlabel('p(1)');ylabel('p(2)');%建立网络net=newc([0 1;0 1],5,0.1); %设置神经元数目为5 %得到网络权值,并在图上绘出figure;plot(P(1,:),P(2,:),'+r');w=net.iw{1}hold on;plot(w(:,1),w(:,2),'ob');hold off;title('输入样本向量及初始权值');xlabel('p(1)');ylabel('p(2)');figure;plot(P(1,:),P(2,:),'+r');hold on;%训练网络net.trainParam.epochs=7;net=init(net);net=train(net,P);%得到训练后的网络权值,并在图上绘出w=net.iw{1}plot(w(:,1),w(:,2),'ob');hold off;title('输入样本向量及更新后的权值');xlabel('p(1)');ylabel('p(2)');a=0;p = [0.6 ;0.8];a=sim(net,p)%生成一个信号,作为被预测信号Time=0:0.025:5;T=sin(Time*4*pi);Q=length(T);%由信号T生成输入信号PP = zeros(5,Q);P(1,2:Q) = T(1,1:(Q-1));P(2,3:Q) = T(1,1:(Q-2));P(3,4:Q) = T(1,1:(Q-3));P(4,5:Q) = T(1,1:(Q-4));P(5,6:Q) = T(1,1:(Q-5));%绘出信号T的曲线figure;plot(Time,T);title('信号T');xlabel('时间');ylabel('目标信号');%设计网络net=newlind(P,T);%仿真网络a=sim(net,P);%绘出网络预测输出figure;plot(Time,a);title('预测结果');xlabel('时间');ylabel('预测值');%得到误差信号,并绘出其曲线e=T-a;figure;plot(Time,e);title('误差');xlabel('时间');ylabel('误差值');%分别定义两段时间Time1和Time2,对应信号的不同频率时段Time1=0:0.05:4;Time2=4.05:0.024:6;Time=[Time1 Time2];%得到待预测的目标信号T=[cos(Time1*4*pi) cos(Time2*8*pi)];T=con2seq(T);%绘出目标信号的曲线,并指定给输入figure;plot(Time,cat(2,T{:}));xlabel('时间');ylabel('目标');title('待跟踪的目标信号');P=T;%生成线性网络lr=0.1;delays = [1 2 3 4 5];net = newlin(minmax(cat(2,P{:})),1,delays,lr);%对网络进行自适应训练[net,a,e]=adapt(net,P,T);%绘出预测信号、目标信号及误差信号曲线figure;plot(Time,cat(2,a{:}),Time,cat(2,P{:}),'--');xlabel('时间');ylabel('目标、预测值');title('目标信号及预测结果');figure;plot(Time,cat(2,e{:}));xlabel('时间');ylabel('误差');title('误差信号');%定义输入信号并绘出其曲线time=0:0.025:5;X=sin(sin(time).*time*10);plot(time,X);title('输入信号T');xlabel('时间');ylabel('输入信号');figure;%定义系统线性变换函数,绘出系统输出曲线T=X*2+0.8;plot(time,T);title('系统输出T');xlabel('时间');ylabel('系统输出');%定义网络输入Q=size(X,2);P=zeros(3,Q);P(1,1:Q)=X(1,1:Q);P(2,2:Q)=X(1,1:(Q-1));P(3,3:Q)=X(1,1:(Q-2));%建立网络net=newlind(P,T);%测试网络a=sim(net,P);%绘出网络输出a与系统输出Tfigure;plot(time,a,'+',time,T,'--');title('网络输出a与系统输出T'); xlabel('时间');ylabel('系统输出-- 网络输出+');%计算误差,并绘出其曲线e=T-a;figure;plot(time,e);title('输出误差');xlabel('时间');ylabel('误差');%定义输入信号并绘出其曲线time1=0:0.005:4;time2=4.005:0.005:6;time=[time1 time2];X=sin(sin(time*4).*time*8);plot(time,X);title('输入信号X');xlabel('时间');ylabel('输入信号');%定义系统输出,绘出曲线steps1=length(time1);[T1,state]=filter([1 -0.5],1,X(1:steps1));steps2=length(time2);T2=filter([0.9 -0.6],1,X((1:steps2) + steps1),state); T=[T1 T2];figure;plot(time,T);title('系统输出T');xlabel('时间');ylabel('系统输出');%将系统输入和输出转换成序列信号T=con2seq(T);P=con2seq(X);%建立网络lr=0.5;delays=[0 1];net=newlin(minmax(cat(2,P{:})),1,delays,lr);%训练网络[net,a,e]=adapt(net,P,T);%绘出网络输出a与系统输出Tfigure;plot(time,cat(2,a{:}),'+',time,cat(2,T{:}),'--');title('网络输出a与系统输出T');xlabel('时间');ylabel('系统输出-- 网络输出+');%绘出误差曲线figure;plot(time,cat(2,e{:}));title('输出误差');xlabel('时间');ylabel('误差');。

BP神经网络算法BP神经网络算法(BackPropagation Neural Network)是一种基于梯度下降法训练的人工神经网络模型,广泛应用于分类、回归和模式识别等领域。
它通过多个神经元之间的连接和权重来模拟真实神经系统中的信息传递过程,从而实现复杂的非线性函数拟合和预测。
BP神经网络由输入层、隐含层和输出层组成,其中输入层接受外部输入的特征向量,隐含层负责进行特征的抽取和转换,输出层产生最终的预测结果。
每个神经元都与上一层的所有神经元相连,且每个连接都有一个权重,通过不断调整权重来优化神经网络的性能。
BP神经网络的训练过程主要包括前向传播和反向传播两个阶段。
在前向传播中,通过输入层将特征向量引入网络,逐层计算每个神经元的输出值,直至得到输出层的预测结果。
在反向传播中,通过计算输出层的误差,逐层地反向传播误差信号,并根据误差信号调整每个连接的权重值。
具体来说,在前向传播过程中,每个神经元的输出可以通过激活函数来计算。
常见的激活函数包括Sigmoid函数、ReLU函数等,用于引入非线性因素,增加模型的表达能力。
然后,根据权重和输入信号的乘积来计算每个神经元的加权和,并通过激活函数将其转化为输出。
在反向传播过程中,首先需要计算输出层的误差。
一般采用均方差损失函数,通过计算预测值与真实值之间的差异来衡量模型的性能。
然后,根据误差信号逐层传播,通过链式法则来计算每个神经元的局部梯度。
最后,根据梯度下降法则,更新每个连接的权重值,以减小误差并提高模型的拟合能力。
总结来说,BP神经网络算法是一种通过多层神经元之间的连接和权重来模拟信息传递的人工神经网络模型。
通过前向传播和反向传播两个阶段,通过不断调整权重来训练模型,并通过激活函数引入非线性因素。
BP 神经网络算法在分类、回归和模式识别等领域具有广泛的应用前景。

bp神经网络激活函数
BP神经网络激活函数是一种模拟机器神经网络的仿生激活函数,用于实现网络的计算。
它的原理和激活函数非常相似,它是一种特殊的无衰减的S形激活函数,以便有增强的收敛能力。
在建立BP神经网络时,激活函数的参数调整将会直接影响网络的性能。
BP神经网络激活函数有快速传播(Fast Propagate,FP)和反向传递(Back Propagate,BP)两个主要部分。
快速传播部分使用S形激活函数,反向传播部分使用反向传播算法(Back Propagate Algorithm,BP)传递感知量,以便调整网络权值。
这种激活函数有助于提高网络的收敛性和拟合性,因此使用它的神经网络的性能相对较好。
在机器学习的BP神经网络建模中,S形激活函数一般分为:Sigmoid、tanh和Rectifier等。
Sigmoid激活函数常用的型号有:Logistic Sigmoid函数(LogSig)和Hyperbolic Tangent函数(tanh),它们都是双曲正切函数的变体,由0~1的范围值向-1~1的范围值缩放而成。
此外,还有一种称为Rectifier激活函数的型号,它是一种正切函数,采用跃变规则,它跟Sigmoid函数类似,只不过其非线性效果较强,拟合精度更高,并且能消除梯度消失的问题,因此,常用来替代Sigmoid等估计。
以上就是BP神经网络激活函数的简介,它是一种模拟机器神经网络的仿生激活函数,具备良好的拟合性、可拓展性和可伸缩性。
它包括快速传播部分和反向传递部分,可以有效解决梯度消失问题,为BP 神经网络提供稳定和有效的收敛性能,是BP神经网络构建和拟合的重要组成部分。

遗传算法优化神经网络-更好拟合函数1.案例背景BP神经网络是一种反向传递并且能够修正误差的多层映射函数,它通过对未知系统的输入输出参数进行学习之后,便可以联想记忆表达该系统。
但是由于BP网络是在梯度法基础上推导出来的,要求目标函数连续可导,在进化学习的过程中熟练速度慢,容易陷入局部最优,找不到全局最优值。
并且由于BP网络的权值和阀值在选择上是随机值,每次的初始值都不一样,造成每次训练学习预测的结果都有所差别。
遗传算法是一种全局搜索算法,把BP神经网络和遗传算法有机融合,充分发挥遗传算法的全局搜索能力和BP神经网络的局部搜索能力,利用遗传算法来弥补权值和阀值选择上的随机性缺陷,得到更好的预测结果。
本案例用遗传算法来优化神经网络用于标准函数预测,通过仿真实验表明该算法的有效性。
2.模型建立2.1预测函数2.2 模型建立遗传算法优化BP网络的基本原理就是用遗传算法来优化BP网络的初始权值和阀值,使优化后的BP网络能够更好的预测系统输出。
遗传算法优化BP网络主要包括种群初始化,适应度函数,交叉算子,选择算子和变异算子等。
2.3 算法模型3.编程实现3.1代码分析用matlabr2009编程实现神经网络遗传算法寻找系统极值,采用cell工具把遗传算法主函数分为以下几个部分:Contents•清空环境变量•网络结构确定•遗传算法参数初始化•迭代求解最佳初始阀值和权值•遗传算法结果分析•把最优初始阀值权值赋予网络预测•BP网络训练•BP网络预测主要的代码段分析如下:3.2结果分析采用遗传算法优化神经网络,并且用优化好的神经网络进行系统极值预测,根据测试函数是2输入1输出,所以构建的BP网络结构是2-5-1,一共去2000组函数的输入输出,用其中的1900组做训练,100组做预测。
遗传算法的基本参数为个体采用浮点数编码法,个体长度为21,交叉概率为0.4,变异概率为0.2,种群规模是20,总进化次数是50次,最后得到的遗传算法优化过程中最优个体适应度值变化如下所示:4 案例扩展4.1 网络优化方法的选择4.2 算法的局限性清空环境变量clcclear网络结构建立%读取数据load data input output%节点个数inputnum=2;hiddennum=5;outputnum=1;%训练数据和预测数据input_train=input(1:1900,:)';input_test=input(1901:2000,:)';output_train=output(1:1900)';output_test=output(1901:2000)';%选连样本输入输出数据归一化[inputn,inputps]=mapminmax(input_train);[outputn,outputps]=mapminmax(output_train);%构建网络net=newff(inputn,outputn,hiddennum);遗传算法参数初始化maxgen=50; %进化代数,即迭代次数sizepop=20; %种群规模pcross=[0.4]; %交叉概率选择,0和1之间pmutation=[0.2]; %变异概率选择,0和1之间%节点总数numsum=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;lenchrom=ones(1,numsum);bound=[-3*ones(numsum,1) 3*ones(numsum,1)]; %数据围%------------------------------------------------------种群初始化--------------------------------------------------------individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]); %将种群信息定义为一个结构体avgfitness=[]; %每一代种群的平均适应度bestfitness=[]; %每一代种群的最佳适应度bestchrom=[]; %适应度最好的染色体%初始化种群for i=1:sizepop%随机产生一个种群individuals.chrom(i,:)=Code(lenchrom,bound); %编码(binary和grey的编码结果为一个实数,float的编码结果为一个实数向量)x=individuals.chrom(i,:);%计算适应度individuals.fitness(i)=fun(x,inputnum,hiddennum,outputnum,net,inputn, outputn); %染色体的适应度end%找最好的染色体[bestfitness bestindex]=min(individuals.fitness);bestchrom=individuals.chrom(bestindex,:); %最好的染色体avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度% 记录每一代进化中最好的适应度和平均适应度trace=[avgfitness bestfitness];迭代求解最佳初始阀值和权值进化开始for i=1:maxgeni% 选择individuals=Select(individuals,sizepop);avgfitness=sum(individuals.fitness)/sizepop;%交叉individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bou nd);% 变异individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizep op,i,maxgen,bound);% 计算适应度for j=1:sizepopx=individuals.chrom(j,:); %解码individuals.fitness(j)=fun(x,inputnum,hiddennum,outputnum,net,inputn, outputn);end%找到最小和最大适应度的染色体及它们在种群中的位置[newbestfitness,newbestindex]=min(individuals.fitness);[worestfitness,worestindex]=max(individuals.fitness);% 代替上一次进化中最好的染色体if bestfitness>newbestfitnessbestfitness=newbestfitness;bestchrom=individuals.chrom(newbestindex,:);endindividuals.chrom(worestindex,:)=bestchrom;individuals.fitness(worestindex)=bestfitness;avgfitness=sum(individuals.fitness)/sizepop;trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度endi =1i =2i =3i =4i =5i =6i =7i =8i =9i =10i =11i =12i =13i =14i =15i =16i =17i =18i =19i =20i =21i =22i =23i =24i =25i =26i =27i =28i =29i =30i =31i =32i =33i =34i =35i =36i =37i =38i =39i =40i =41i =42i =43i =44i =45i =46i =47i =48i =49i =50遗传算法结果分析figure(1)[r c]=size(trace);plot([1:r]',trace(:,2),'b--');title(['适应度曲线 ''终止代数=' num2str(maxgen)]); xlabel('进化代数');ylabel('适应度');legend('平均适应度','最佳适应度');disp('适应度变量');x=bestchrom;Warning: Ignoring extra legend entries.适应度变量把最优初始阀值权值赋予网络预测%用遗传算法优化的BP网络进行值预测w1=x(1:inputnum*hiddennum);B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hidd ennum*outputnum);B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hidd ennum+hiddennum+hiddennum*outputnum+outputnum);net.iw{1,1}=reshape(w1,hiddennum,inputnum);net.lw{2,1}=reshape(w2,outputnum,hiddennum);net.b{1}=reshape(B1,hiddennum,1);net.b{2}=B2;BP网络训练%网络进化参数net.trainParam.epochs=100;net.trainParam.lr=0.1;%net.trainParam.goal=0.00001;%网络训练net=train(net,inputn,outputn);BP网络预测%数据归一化inputn_test=mapminmax('apply',input_test,inputps);an=sim(net,inputn_test);test_simu=mapminmax('reverse',an,outputps);error=test_simu-output_test;figure(2)plot(error)k=error./output_testk =Columns 1 through 9-0.0003 0.0010 0.0003 0.0001 0.0002 -0.0005 0.0003 0.0003 0.0109Columns 10 through 18-0.0007 -0.0003 0.0002 -0.0008 -0.0015 -0.0002 0.0011 0.0002 0.0004Columns 19 through 270.0002 0.0003 -0.0000 0.0000 -0.0004 -0.0004 0.0005 0.0001 0.0023Columns 28 through 36-0.0000 -0.0003 0.0000 -0.0005 -0.0002 0.0003 -0.0002 -0.0002 0.0001Columns 37 through 450.0001 0.0002 0.0002 0.0011 -0.0004 -0.0006 0.0002 0.0000 0.0000Columns 46 through 540.0001 0.0001 0.0000 -0.0001 0.0016 0.0002 -0.0003 -0.0000 -0.0000Columns 55 through 630.0000 0.0003 -0.0004 0.0001 0.0002 0.0002 0.0002 0.0000 0.0002Columns 64 through 720.0002 -0.0001 0.0003 0.0005 0.0002 -0.0003 -0.0001 -0.0000 0.0002Columns 73 through 810.0000 -0.0002 -0.0002 0.0002 -0.0000 -0.0003 0.0001 -0.0001 0.0006Columns 82 through 90-0.0006 0.0003 0.0068 -0.0005 0.0001 -0.0001 -0.0001 -0.0010 -0.0002Columns 91 through 990.0001 0.0002 -0.0000 0.0003 0.0000 0.0000 -0.0003 -0.0001 0.0003Column 100-0.0004。

BP神经⽹络拟合函数BP神经⽹络⽤于函数拟合的实验⼀、实验⽬的本实验要求掌握前向型神经⽹络的基本⼯作原理及利⽤反向传播确定权系数的⽅法,并能在MATLAB仿真环境下设计相应的神经⽹络,实现对⾮线性函数的逼近与拟合,并分析影响函数拟合效果的相关因素。
⼆、实验要求设计神经⽹络的基本结构与激励函数,实现对⾮线性函数y=sin(x)的逼近与拟合,并分析影响函数拟合效果的相关参数(包括激励函数的选择sigmoid、线性函数、权系数的初值、步长的⼤⼩、训练样本的多少等),并对⽐实验效果。
三、实验步骤1. 确定神经⽹络的结构本次实验采⽤前向型BP神经⽹络,神经元分层排列,每⼀层的神经元只接受前⼀层神经元的输⼊。
输⼊模式经过各层的顺序变换后,得到输出层输出。
各神经元之间不存在反馈。
该实验神经⽹络含输⼊层和输出层两层神经元,其中输⼊层含六个神经元,输出层含⼀个神经元。
输⼊信号传输到输⼊层,在输出层得到拟合结果。
2.确定采⽤的激励函数、拟合⽅法选择激励函数为sigmoid的函数,因其便于求导,且值域在(0,1)之间,具有较好的收敛特性。
拟合⽅法采⽤梯度下降法,该⽅法使试验数值沿梯度⽅向增加有限步长,避免了盲⽬搜索,提⾼搜索效率。
3.训练流程1)初始化各参数2)开始训练3)计算误差4)计算⼴义误差5)调整连接权系数,直到误差⼩于设定值6)编写程序实现对⾮线性函数y=sin(x)的逼近与拟合算法流程图如图4.1所⽰。
四、实验结果及分析通过BP⽹络学习逼近sin(x)函数的实验发现,不同的初值对逼近效果有较⼤影响。
权系数初值随机选取时,多次运⾏程序,得到⼀组较好的拟合结果(见图1),其权系数为w1 =[-2.9880,-1.9267,-1.3569,-1.5064,-0.6377,-2.3899]w2=[2.0316,2.1572,-1.1427,-1.3108,-0.6328,-1.8135],阈值yw1=[-11.3291,-4.0186,-6.6926,-7.6080,-0.5955,-2.1247],yw2 =-0.4377。
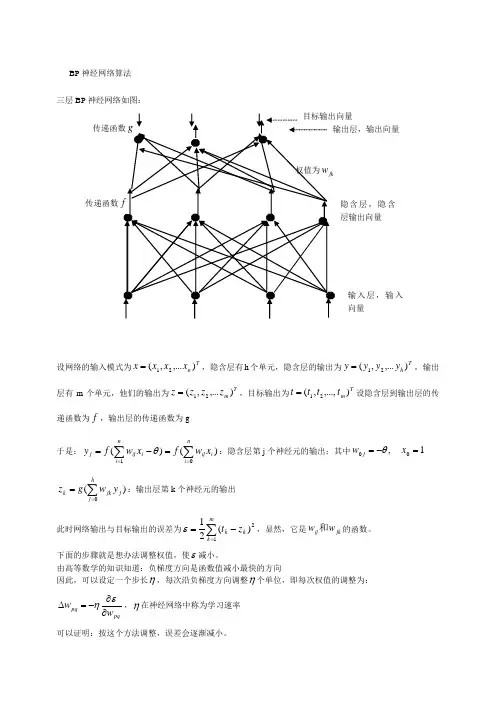
BP 神经网络算法 三层BP 神经网络如图:设网络的输入模式为Tn x x x x ),...,(21=,隐含层有h 个单元,隐含层的输出为Th y y y y ),...,(21=,输出层有m 个单元,他们的输出为Tm z z z z ),...,(21=,目标输出为Tm t t t t ),...,,(21=设隐含层到输出层的传递函数为f ,输出层的传递函数为g于是:)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ:隐含层第j 个神经元的输出;其中1,00=-=x w j θ)(0∑==hj j jk k y w g z :输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε,显然,它是jk ij w w 和的函数。
下面的步骤就是想办法调整权值,使ε减小。
由高等数学的知识知道:负梯度方向是函数值减小最快的方向因此,可以设定一个步长η,每次沿负梯度方向调整η个单位,即每次权值的调整为:pqpq w w ∂∂-=∆εη,η在神经网络中称为学习速率 可以证明:按这个方法调整,误差会逐渐减小。
隐含层,隐含层输出向量传递函数输入层,输入向量BP 神经网络(反向传播)的调整顺序为: 1)先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0-------复合函数偏导公式若取x e x f x g -+==11)()(,则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为: 2)从输入层到隐含层的权值调整迭代公式为: 其中j u 为隐含层第j 个神经元的输入:∑==ni i ijj x wu 0注意:隐含层第j 个神经元与输出层的各个神经元都有连接,即jy ∂∂ε涉及所有的权值ij w ,因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是:因此从输入层到隐含层的权值调整迭代为公式为: 例:下表给出了某地区公路运力的历史统计数据,请建立相应的预测模型,并对给出的2010和2011年的数据,预测相应的公路客运量和货运量。
神经网络激活函数[BP神经网络实现函数逼近的应用分析]神经网络激活函数是神经网络中非常重要的组成部分,它决定了神经网络的非线性特性,并且对于神经网络的求解效果和性能有着重要的影响。
本文将对神经网络激活函数进行详细的分析和探讨,并以BP神经网络实现函数逼近的应用为例进行具体分析。
1.神经网络激活函数的作用(1)引入非线性:神经网络通过激活函数引入非线性,使其具备处理非线性问题的能力,能够更好的逼近任意非线性函数。
(2)映射特征空间:激活函数可以将输入映射到另一个空间中,从而更好地刻画特征,提高神经网络的表达能力,并且可以保留原始数据的一些特性。
(3)增强模型的灵活性:不同的激活函数具有不同的形状和性质,选择合适的激活函数可以增加模型的灵活性,适应不同问题和数据的特点。
(4)解决梯度消失问题:神经网络中经常会遇到梯度消失的问题,通过使用合适的激活函数,可以有效地缓解梯度消失问题,提高神经网络的收敛速度。
2.常用的神经网络激活函数(1)Sigmoid函数:Sigmoid函数是一种常用的激活函数,它的输出值范围在(0,1)之间,具有平滑性,但是存在梯度消失问题。
(2)Tanh函数:Tanh函数是Sigmoid函数的对称形式,它的输出值范围在(-1,1)之间,相对于Sigmoid函数来说,均值为0,更符合中心化的要求。
(3)ReLU函数:ReLU函数在输入为负数时输出为0,在输入为正数时输出为其本身,ReLU函数简单快速,但是容易出现神经元死亡问题,即一些神经元永远不被激活。
(4)Leaky ReLU函数:Leaky ReLU函数是对ReLU函数的改进,当输入为负数时,输出为其本身乘以一个小的正数,可以解决神经元死亡问题。
(5)ELU函数:ELU函数在输入为负数时输出为一个负有指数衰减的值,可以在一定程度上缓解ReLU函数带来的神经元死亡问题,并且能够拟合更多的函数。
3.BP神经网络实现函数逼近的应用BP神经网络是一种常用的用于函数逼近的模型,它通过不断调整权重和偏置来实现对目标函数的拟合。
基于BP神经网络的磁滞回线的曲线拟合
卢立中;孙宇新;王纪俊
【期刊名称】《大学物理实验》
【年(卷),期】2004(017)004
【摘要】BP神经网络通过调节连接权重可以实现以任意精度逼近非线性函数,利用这一特点可对非线性函数关系进行拟合.本文利用BP神经网络对测定磁滞回线实验中的数据进行处理,结果表明该方法处理结果精度高,拟合效果好,计算机处理程序通用.
【总页数】3页(P70-72)
【作者】卢立中;孙宇新;王纪俊
【作者单位】江苏大学理学院,镇江,2120l;江苏大学电气信息工程学院,镇
江,212013;江苏大学理学院,镇江,2120l
【正文语种】中文
【中图分类】O4-39
【相关文献】
1.基于优化的GRNN和BP神经网络的磁滞曲线拟合对比分析 [J], 何汉林;孟爱华;祝甲明;宋红晓
2.基于BP神经网络的弗兰克-赫兹实验曲线拟合 [J], 王蕴杰
3.基于BP神经网络和EKF神经网络在曲线拟合性能上的对比分析研究 [J], 张彬;陈晓宁;赵金龙;黄立洋
4.基于LMBP神经网络的涡流传感器曲线拟合研究 [J], 丁硕;胡庆功;常晓恒;巫庆
辉
5.基于GABP神经网络曲线拟合的快沿电磁脉冲信号源模型求解 [J], 纪志强;魏明;吴启蒙;樊高辉;魏晗
因版权原因,仅展示原文概要,查看原文内容请购买。
神经网络作业作业说明第一题(函数逼近):BP网络和RBF网络均是自己编写的算法实现。
BP网络均采用的三层网络:输入层(1个变量)、隐层神经元、输出层(1个变量)。
转移函数均为sigmoid函数,所以没有做特别说明。
在第1小题中贴出了BP和RBF的Matlab代码,后面的就没有再贴出;而SVM部分由于没有自己编写,所以没有贴出。
而针对其所做的各种优化或测试,都在此代码的基础上进行,相应参数的命名方式也没有再改变。
RBF网络使用了聚类法和梯度法两种来实现。
而对于SVM网络,在后面两题的分类应用中都是自己编写的算法实现,但在本题应用于函数逼近时,发现效果很差,所以后来从网上下载到一个SVM工具包LS-SVMlab1.5aw,调用里面集成化的函数来实现的,在本题函数逼近中均都是采用高斯核函数来测试的。
第二题(分类):BP网络和RBF网络都是使用的Matlab自带的神经网络工具包来实现的,不再贴出代码部分。
而SVM网络则是使用的课上所教的算法来实现的,分别测试了多项式核函数和高斯核函数两种实现方法,给出了相应的Matlab代码实现部分。
第三题:由于问题相对简单,所以就没有再使用Matlab进行编程实现,而是直接进行的计算。
程序中考虑到MATLAB处理程序的特性,尽可能地将所有的循环都转换成了矩阵运算,大大加快了程序的运行速度。
编写时出现了很多错误,常见的如矩阵运算维数不匹配,索引值超出向量大小等;有时候用了很麻烦的运算来实现了后来才知道原来可以直接调用Matlab里面的库函数来实现以及怎么将结果更清晰更完整的展现出来等等。
通过自己编写算法来实现各个网络,一来提升了我对各个网络的理解程度,二来使我熟悉了Matlab环境下的编程。
1.函数拟合(分别使用BP,RBF,SVM),要求比较三个网络。
2π.x ,05x)sin(5x)exp(y(x)4π.x ,0xsinx y(x)100.x x),1exp(y(x)100.x ,1x1y(x)≤≤-=≤≤=≤≤-=≤≤=解:(1).1001,1)(≤≤=x x x ya. BP 网络:Matlab 代码如下:nv=10; %神经元个数:10个err=0.001; %误差阈值J=1; %误差初始值N=1; %迭代次数u=0.2; %学习率wj=rand(1,nv); %输入层到隐层神经元的权值初始化wk=rand(1,nv); %隐层神经元到输出层的权值初始化xtrain=1:4:100; %训练集,25个样本xtest=1:1:100; %测试集,100个dtrain=1./xtrain; %目标输出向量,即教师%训练过程while (J>err)&&(N<100000)uj=wj'*xtrain;h=1./(1+exp(-uj)); %训练集隐层神经元输出uk=wk*h;y=1./(1+exp(-uk)); %训练集输出层实际输出delta_wk = u*(dtrain-y).*y.*(1-y)*h'; %权值调整delta_wj = u*wk.*(((dtrain-y).*y.*(1-y).*xtrain)*(h.*(1-h))'); wk = wk+delta_wk;wj = wj+delta_wj;J=0.5*sum((dtrain-y).^2); %误差计算j(N)=J;N=N+1;end%测试及显示uj=wj'*xtest;h=1./(1+exp(-uj));uk=wk*h;dtest=1./(1+exp(-uk));figuresubplot(1,2,1),plot(xtest,dtest,'ro',xtest,1./xtest);legend('y=1/x', 'network output');subplot(1,2,2),plot(xtest,1./xtest-dtest);x=1:N-1;figureplot(x,j(x));运行条件:10个神经元,误差迭代阈值为0.001.学习率为0.2。
神经网络实验报告基于BP网络的曲线拟合学院:控制学院*名:***学号: ********2015年6月一、实验目的⑴掌握BP神经网络的权值修改规则⑵利用BP网络修改权值对y=sin(x)曲线实现拟合二、实验要求人工神经网络是近年来发展起来的模拟人脑生物过程的人工智能技术,具有自学习、自组织、自适应和很强的非线性映射能力。
在人工神经网络的实际应用中,常采用BP神经网络或它的变化形式,BP神经网络是一种多层神经网络,因采用BP算法而得名,主要应用于模式识别和分类、函数逼近、数据压缩等领域。
BP网络是一种多层前馈神经网络,由输入层、隐层和输出层组成。
层与层之间采用全互连方式,同一层之间不存在相互连接,隐层可以有一个或多个。
BP算法的学习过程由前向计算过程和误差反向传播过程组成,在前向计算过程中,输入信息从输入层经隐层逐层计算,并传向输出层,每层神经元的状态只影响下一层神经元的状态。
如输出层不能得到期望的输出,则转入误差反向传播过程,误差信号沿原来的连接通路返回,通过修改各层的神经元的权值,使得网络系统误差最小,最终实现网络的实际输出与各自所对应的期望输出逼近。
三、实验内容3.1 训练数据导入要对BP网络进行训练,必须准备训练样本。
对样本数据的获取,可以通过用元素列表直接输入、创建数据文件,从数据文件中读取等方式,具体采用哪种方法,取决于数据的多少,数据文件的格式等。
本文采用直接输入100个样本数据的方式,同时采用归一化处理,可以加快网络的训练速度。
将输入x和输出y都变为-1到1之间的数据,归一化后的训练样本如下图:3.2 网络初始化根据系统输入输出序列,确定网络输入层节点数为1,隐含层节点数H 为20,输出层节点数为1。
初始化输入层、隐含层和输出层神经元之间的连接权值ij w ,jk v ,初始化隐含层阈值0t ,输出层阈值1t ,给定学习速率0a ,1a 和u ,给定算法迭代次数inum 和最大可接受误差error ,同时给定神经元激励函数sigmoid 。
基于BP神经网络算法的函数逼近神经网络是一种基于生物神经元工作原理构建的计算模型,可以通过学习和调整权重来逼近非线性函数。
其中,基于误差反向传播算法(BP)的神经网络是最常见和广泛应用的一种,其能够通过反向传播来调整网络的权重,从而实现对函数的近似。
BP神经网络的算法包括了前馈和反向传播两个过程。
前馈过程是指输入信号从输入层经过隐藏层传递到输出层的过程,反向传播过程是指将网络输出与实际值进行比较,并根据误差来调整网络权重的过程。
在函数逼近问题中,我们通常将训练集中的输入值作为网络的输入,将对应的目标值作为网络的输出。
然后通过反复调整网络的权重,使得网络的输出逼近目标值。
首先,我们需要设计一个合适的神经网络结构。
对于函数逼近问题,通常使用的是多层前馈神经网络,其中包括了输入层、隐藏层和输出层。
隐藏层的神经元个数和层数可以根据具体问题进行调整,一般情况下,通过试验和调整来确定最优结构。
然后,我们需要确定误差函数。
对于函数逼近问题,最常用的误差函数是均方误差(Mean Squared Error)。
均方误差是输出值与目标值之间差值的平方和的均值。
接下来,我们进行前馈过程,将输入值通过网络传递到输出层,并计算出网络的输出值。
然后,我们计算出网络的输出与目标值之间的误差,并根据误差来调整网络的权重。
反向传播的过程中,我们使用梯度下降法来最小化误差函数,不断地调整权重以优化网络的性能。
最后,我们通过不断训练网络来达到函数逼近的目标。
训练过程中,我们将训练集中的所有样本都输入到网络中,并根据误差调整网络的权重。
通过反复训练,网络逐渐优化,输出值逼近目标值。
需要注意的是,在进行函数逼近时,我们需要将训练集和测试集分开。
训练集用于训练网络,测试集用于评估网络的性能。
如果训练集和测试集中的样本有重叠,网络可能会出现过拟合现象,导致在测试集上的性能下降。
在神经网络的函数逼近中,还有一些注意事项。
首先是选择适当的激活函数,激活函数能够在网络中引入非线性,使网络能够逼近任意函数。
BP神经网络用于函数拟合的实验
一、实验目的
本实验要求掌握前向型神经网络的基本工作原理及利用反向传播确定权系数的方法,并能在MATLAB仿真环境下设计相应的神经网络,实现对非线性函数的逼近与拟合,并分析影响函数拟合效果的相关因素。
二、实验要求
设计神经网络的基本结构与激励函数,实现对非线性函数y=sin(x)的逼近与拟合,并分析影响函数拟合效果的相关参数(包括激励函数的选择sigmoid、线性函数、权系数的初值、步长的大小、训练样本的多少等),并对比实验效果。
三、实验步骤
1. 确定神经网络的结构
本次实验采用前向型BP神经网络,神经元分层排列,每一层的神经元只接受前一层神经元的输入。
输入模式经过各层的顺序变换后,得到输出层输出。
各神经元之间不存在反馈。
该实验神经网络含输入层和输出层两层神经元,其中输入层含六个神经元,输出层含一个神经元。
输入信号传输到输入层,在输出层得到拟合结果。
2.确定采用的激励函数、拟合方法
选择激励函数为sigmoid的函数,因其便于求导,且值域在(0,1)之间,具有较好的收敛特性。
拟合方法采用梯度下降法,该方法使试验数值沿梯度方向增加有限步长,避免了盲目搜索,提高搜索效率。
3.训练流程
1)初始化各参数
2)开始训练
3)计算误差
4)计算广义误差
5)调整连接权系数,直到误差小于设定值
6)编写程序实现对非线性函数y=sin(x)的逼近与拟合
算法流程图如图4.1所示。
四、实验结果及分析
通过BP网络学习逼近sin(x)函数的实验发现,不同的初值对逼近效果有较大影响。
权系数初值随机选取时,多次运行程序,得到一组较好的拟合结果(见图1),其权系数为w1 =[-2.9880,-1.9267,-1.3569,-1.5064,-0.6377,-2.3899]
w2=[2.0316,2.1572,-1.1427,-1.3108,-0.6328,-1.8135],阈值yw1
=[-11.3291,-4.0186,-6.6926,-7.6080,-0.5955,-2.1247],yw2 =-0.4377。
图1
固定选取初值为较好的拟合结果的权系数w1,w2及阈值yw1,yw2,改变其学习步长,发现适当步长可以使网络拟合得更好,但过小及过大的步长都会加大误差(见图2.1,图2.2,图2.3),图2.1设置的步长为0.2,最终拟合误差在0.1左右,图2.2设置的步长为0.02,最终拟合误差接近0.02,图2.3设置的步长为0.002,最终拟合误差在0.03左右。
由此可见,步长在0.02时,拟合得最好,误差最低。
图 2.1
图 2.2
图 2.3
固定选取初值为较好的拟合结果的权系数w1,w2及阈值yw1,yw2,取步长为0.02,改变样本数n,发现适当样本数可以使网络拟合得更好(见图3.1,图3.2,图3.3),图3.1设置的样本数为10,最终拟合误差虽然趋近于0,但通过图像我们可以直观地看出,样本数过少使BP网络拟合出的是分段函数,而不是平滑的sin(x),图3.2设置的样本数为30,最终拟合误差接近0.02,图2.3设置的样本数为300,最终拟合误差接近0.004,但是通过逼近图像可以直观看到,300的样本数拟合程度并不如30样本数的好。
可见,样本数为30时,拟合得最好,误差最低。
图 3.1 图 3.2
图 3.3
固定选取初值为较好的拟合结果的权系数w1,w2及阈值yw1,yw2,取步长为0.02,样本数为30,改变学习次数,发现学习次数越多,BP网络拟合越好,但是达到一定程度后,因为学习要求的存在(均方差小于0.008),学习次数对拟合性的影响便会达到饱和,增加学习次数对拟合程度影响不大(见图4.1,图4.2,图4.3)。
图4.1设置的学习次数为3000,最终拟合误差接近0.02,图4.2设置的学习次数为30000,最终拟合误差0.02左右,图4.3设置的学习次数为300000,最终拟合误差还是在0.02左右。
可见,学习次数为30000时,就已经足够。
图 4.1 图 4.2
图 4.3
通过以上实验对比发现,选取初值为较好的拟合结果的权系数w1,w2及阈值yw1,yw2,取步长为0.02,样本数为30,学习次数为30000,在不改变BP网络内部结构的情况下拟合程度最好。
改变BP网络结构,把第一层6个神经元改为3个神经元,权系数和阈值初值随机选取,步长0.02,样本数30,选取学习次数为3000时(如图5.1),可以发现拟合度十分差,而最大学习次数到30000时(如图5.2),拟合程度改善不少,最终误差接近于0,进一步证明学习次数越大,BP网络拟合程度比较好。
图 5.1
图 5.2
改变BP网络结构,把第二层神经元的激励函数改为sigmoid函数,第一层神经元依然为6个,权系数和阈值初值随机选取,步长0.02,样本数30,选取学习次数为3000
时(如图6.1),可以发现拟合度十分差,而最大学习次数到30000时(如图6.2),拟合程度改善不少。
但激励函数改为sigmoid函数后,发现BP网络只能拟合sin(x)的前半周期,后半周期输出都为0,这是因为sigmoid函数的值域为[0,1],而sin(x)函数的值域为[-1,1],所以输出层的激励函数不能为sigmoid函数,否则无法拟合sin后半周期。
图 6.1
图 6.2
通过以上实验对比,第一层6个神经元,激励函数为sigmoid函数,第二层1个神经元,激励函数为线性函数,步长0.02,样本数30,选取学习次数为30000时,BP网络拟合sin函数程度最好。
四、MATLAB编程代码
function bpsin
%用BP神经网络拟合sin(x)函数,两层神经元,第一层六个,激励函数为sigmoid函数,第二层一个,激励函数为线性函数。
%********初始化*******************************
l=0.2; %学习步长
n=30; %输入样本数
cell=6; %第一层神经元数
times=3000; %学习次数
x=(linspace(0,2*pi,n));%选取样本点
t=sin(x); %学习拟合的函数
w1=rand(cell,1)*0.05; %第一层连接权系数的初始值
w2=rand(1,cell)*0.05; %第二层连接权系数的初始值
yw1=rand(cell,1)*0.05; %第一层阈值初始值
yw2=rand*0.05; %第二层阈值初始值
y=rand(1,n)*0.05; %输出初始值
counts=1; %计数
e=zeros(1,times); %均方差
%***************学习过程*************************
for i=1:times
ei=0;
for a=1:n %遍历样本
net1=w1*x(a)-yw1;
out=logsig(net1); %第一层输出
net2=w2*out-yw2;
%y(a)=logsig(net2);
y(a)=net2; %第二层输出(y)
%det2=(t(a)-y(a))*y(a)*(1-y(a));
det2=(t(a)-y(a));
%det2
det1=((det2*(w2)').*out).*(1-out);
w1=w1+det1*x(a)*l; %更新权系数
w2=w2+(det2*out)'*l;
yw1=-det1*l+yw1;
yw2=-det2*1+yw2;
ei=ei+det2^2/2; %累积误差
e(i)=ei;
end
if ei<0.008
break;
end
counts=counts+1;
end
%************逼近曲线****************
for a=1:n
net1=w1*x(a)-yw1;
out=logsig(net1);
net2=w2*out-yw2;
%y(a)=logsig(net2);
y(a)=net2;
end
%***********画图*******************
subplot(2,1,1)
plot(x,t,'b-',x,y,'k*-'); %画sin函数及bp拟合图grid on;
title('BP method, y=sin(x)');
xlabel('x');
ylabel('y=sin(x)');
if(counts<times)
count=1:counts;
sum=counts;
else
count=1:times;
sum=times;
end
subplot(2,1,2);
plot(count,e(1:sum)); %画误差图grid on;
title('BP算法学习曲线');
xlabel('迭代次数');
ylabel('均方误差');
end。