九年级上册第一章达标测试卷及答案
- 格式:doc
- 大小:178.00 KB
- 文档页数:7

沪教版九年级化学上册第一章综合测试卷一、选择题(每小题只有一个正确答案,每小题3分,共45分)1.下列对重要化学研究成果的介绍中,错误的是()A.道尔顿提出了原子论B.拉瓦锡发现了电子C.门捷列夫提出了元素周期律D.阿伏伽德罗提出了分子假说2.明确各种化学仪器的基本用途并熟练使用,是化学实验的基本要求之一。
下列仪器可以用于直接加热的是()3.[2024泰州一模]书法之美尽在笔墨纸砚之间,下列过程涉及化学变化的是()A.择笔刻字B.燃脂制墨C.裁剪宣纸D.砚台研墨4.[2024沈阳一模]下列化学观念中,不正确的是()A.物质的性质决定了物质的用途B.所有物质都能无条件进行转化C.物质既有天然存在的也有人工创造的D.化学变化中有新物质生成5.下列物质的性质属于化学性质的是()A.蔗糖能溶于水B.氢气能被点燃C.铜丝具有导电性D.食盐有咸味6.某同学将鸡蛋壳放入食醋中,发现有气泡产生,他认为可能是产生了二氧化碳气体。
就“可能是产生了二氧化碳气体”而言,属于科学探究中的()A.作出猜想B.设计实验C.进行实验D.得出结论7.下列物质中,所含元素种类最多的是()A.金刚石(C) B.二氧化碳(CO2)C.氨气(NH3) D.碳酸氢铵(NH4HCO3)8.[2024泉州模拟]下列符合实验室安全规则的是()A.用漏斗直接向燃着的酒精灯内添加酒精B.实验室中没有腐蚀性的试剂,可用手抓取C.加热试管中的液体,要从侧面观察实验现象D.实验室中未经老师允许,可自行动手做实验9.[2024重庆]试管是实验室常用的仪器。
下列有关试管的使用正确的是()10.在做“镁条在空气中燃烧”的实验时,需要用到下列仪器中的()①试管夹②酒精灯③陶土网④烧杯⑤铁架台⑥坩埚钳⑦药匙⑧镊子A.①②⑦B.①②③⑧C.②③④⑤D.②③⑥⑧11.[2024深圳模拟改编]2024年“中国航天日”的主题是“极目楚天,共襄星汉”。
下列有关航天的课题属于化学学科研究领域的是()A.“嫦娥二号”探月卫星轨道的计算B.“神舟十八号”载人飞船与天和核心舱对接C.“长征二号F”运载火箭所需新型材料的研制与生产D.“祝融号”火星车与“天问一号”火星探测器之间的信息传递12.[2024威海期末改编]酒精灯是实验室常用的加热仪器。
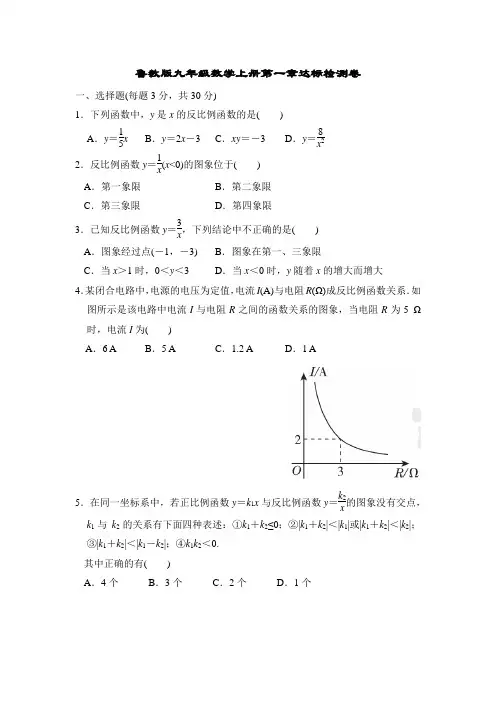
鲁教版九年级数学上册第一章达标检测卷一、选择题(每题3分,共30分)1.下列函数中,y是x的反比例函数的是()A.y=15x B.y=2x-3 C.xy=-3 D.y=8x22.反比例函数y=1x(x<0)的图象位于()A.第一象限B.第二象限C.第三象限D.第四象限3.已知反比例函数y=3x,下列结论中不正确的是()A.图象经过点(-1,-3) B.图象在第一、三象限C.当x>1时,0<y<3 D.当x<0时,y随着x的增大而增大4.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例函数关系.如图所示是该电路中电流I与电阻R之间的函数关系的图象,当电阻R为5 Ω时,电流I为()A.6 A B.5 A C.1.2 A D.1 A5.在同一坐标系中,若正比例函数y=k1x与反比例函数y=k2x的图象没有交点,k1与k2的关系有下面四种表述:①k1+k2≤0;②|k1+k2|<|k1|或|k1+k2|<|k2|;③|k1+k2|<|k1-k2|;④k1k2<0.其中正确的有()A.4个B.3个C.2个D.1个6.已知点A(-1,y1),B(2,y2)都在双曲线y=3+mx上,且y1>y2,则m的取值范围是()A.m<0 B.m>0 C.m>-3 D.m<-37.y=ax+b与y=a-bx,其中ab<0,a,b为常数,它们在同一坐标系中的图象可以是()8.如图,分别过反比例函数y=2x(x>0)的图象上任意两点A,B作x轴的垂线,垂足分别为点C,D,连接OA,OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1,S2,则S1与S2的大小关系是()A.S1>S2B.S1<S2C.S1=S2D.不能确定9.如图,在平面直角坐标系中,点A是双曲线y1=k1x(x>0)上任意一点,连接AO,过点O作AO的垂线与双曲线y2=k2x(x<0)交于点B,连接AB,已知AOBO=2,则k1k2=()A.4 B.-4 C.2 D.-210.反比例函数y=ax(a>0,a为常数)和y=2x在第一象限内的图象如图所示,点M在y=ax的图象上,MC⊥x轴于点C,交y=2x的图象于点A;MD⊥y轴于点D,交y=2x的图象于点B.当点M在y=ax(x>0)的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,点B是MD的中点.其中正确结论有()A.0个B.1个C.2个D.3个二、填空题(每题3分,共24分)11.已知一个反比例函数的图象经过点(3,1),若该反比例函数的图象也经过点(-1,m ),则m =________.12.若点(2,y 1),(3,y 2)在函数y =-2x 的图象上,则y 1________y 2(填“>”“<”或“=”).13.若反比例函数y =k x 的图象与一次函数y =mx 的图象的一个交点的坐标为(1,2),则另一个交点的坐标为________.14.某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p (kPa)是气体体积V (m 3)的反比例函数,其图象如图所示,则当气球内气体体积V (m 3)的范围是0.8<V <2时,气体的压强p (kPa)的范围是________.15.如图,点A 是反比例函数图象上一点,过点A 作AB ⊥y 轴于点B ,点P 在x 轴上,且△ABP 的面积为6,则这个反比例函数的表达式为________.16.如图,已知矩形ABCD ,AB 在x 轴的正半轴上(点A 与点O 重合),AB =3,BC =1,连接AC ,BD ,交点为M .将矩形ABCD 沿x 轴向右平移,当平移距离为________时,点M 在反比例函数y =1x 的图象上.17.如图,点A 在反比例函数y =k x (x >0)的图象上,点B 在x 轴负半轴上,直线AB 交y 轴于点C ,若AC BC =12,△AOB 的面积为6,则k 的值为________.18.如图,在反比例函数y =10x (x >0)的图象上,有一系列点A 1,A 2,A 3,…,A n ,A n +1,若点A 1,A 2,A 3,…的横坐标分别为2,4,6,…,现分别过点A 1,A 2,A 3,…,A n ,A n +1作x 轴、y 轴的垂线段,构成若干个矩形,将图中阴影部分的面积从左到右依次记为S 1,S 2,S 3,…,S n ,则S 1=________,S 1+S 2+S 3+…+S n =________(用含n 的代数式表示).三、解答题(19~21题每题8分,22~24题每题10分,25题12分,共66分) 19.南宁至玉林高速铁路已于2019年开工建设.玉林良睦隧道是全线控制性工程,首期工程的土石方总量为600千立方米,计划平均每天挖掘土石方x千立方米,需用时间y天,且完成首期工程限定时间不超过600天.(1)求y与x之间的函数关系式及自变量x的取值范围;(2)由于工程进度的需要,实际平均每天挖掘土石方比原计划多0.2千立方米,工期比原计划提前了100天完成,求实际挖掘了多少天才能完成首期工程.20.如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=mx(m为常数且m≠0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,若OB=2OA=3OD=6.(1)求一次函数与反比例函数的表达式;(2)求两个函数图象的另一个交点E的坐标;(3)请观察图象,直接写出不等式kx+b≤mx的解集.21.如图,已知四边形OABC是菱形,OC在x轴上,点B的坐标为(18,6),反比例函数y=kx(k≠0)的图象经过点A,与OB交于点E.(1)求k的值;(2)求OEEB的值.22.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-8 x的图象交于A(-2,b),B两点.(1)求一次函数的表达式;(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.23.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,点A,C分别在y轴、x轴上,点B的坐标为(4,2),直线y=-12x+3分别交AB,BC于点M,N,反比例函数y=kx(x>0)的图象经过点M,N.(1)求反比例函数的表达式;(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.24.小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系,完成第3次训练所需时间为400秒.(1)求y与x之间的函数关系式;(2)当x的值为6,8,10时,对应的函数值分别为y1,y2,y3,比较(y1-y2)与(y2-y3)的大小:y1-y2________y2-y3(填“>”“<”或“=”).25.如图,一次函数y=x+3的图象与反比例函数y=kx(x>0)的图象相交于点A(1,m),与x轴相交于点B.(1)求这个反比例函数的表达式;(2)C为反比例函数的图象上异于点A的一点,直线AC交x轴于点D,设直线AC所对应的函数表达式为y=nx+b.①若△ABD的面积为12,求n,b的值;②作CE⊥x轴,垂足为E,记t=OE·DE,求n·t的值.答案一、1.C 2.C 3.D 4.C5.B【点拨】若k1>0,则正比例函数的图象经过一、三象限,∵在同一坐标系中,正比例函数y=k1x与反比例函数y=k2x的图象没有交点,∴反比例函数的图象经过二、四象限,则k2<0;若k1<0,则正比例函数的图象经过二、四象限,∴反比例函数的图象经过一、三象限,则k2>0,综上可知k1和k2异号.①∵k1和k2的绝对值的大小未知,∴k1+k2≤0不一定成立,故①错误;②|k1+k2|=||k1|-|k2||<|k1|或|k1+k2|=||k1|-|k2||<|k2|,故②正确;③|k1+k2|=||k1|-|k2||<||k1|+|k2||=|k1-k2|,故③正确;④∵k1和k2异号,∴k1k2<0,故④正确.故正确的有3个,故选B.6.D【点拨】由题意知,反比例函数图象在第二、四象限,所以3+m<0,即m<-3.7.C8.C【点拨】∵点A,B均在反比例函数y=2x(x>0)的图象上,∴S△AOC=S△BOD=1.由题图可知,△COE是△AOC与△BOD的公共部分,因此△AOE与梯形ECDB 的面积相等,即S1=S2,故选C.9.B【点拨】如图,作AD⊥x轴于点D,BE⊥x轴于点E.∵点A是双曲线y1=k1x(x>0)上的点,点B是双曲线y2=k2x(x<0)上的点,∴S△AOD=12|k1|=12k1,S△BOE=12|k2|=-12k2.∵∠AOB=90°,∴∠BOE+∠AOD=90°.又∵∠AOD +∠OAD =90°,∴∠BOE =∠OAD .又∵∠BEO =∠ODA =90°.∴△BOE ∽△OAD .∴S △AOD S △BOE =⎝ ⎛⎭⎪⎫OA OB 2.∴12k 1-12k 2=22. ∴k 1k 2=-4.故选B. 10.D 【点拨】∵点A ,B 在同一反比例函数y =2x 的图象上,∴S △ODB =S △OCA=12×2=1,∴①正确;∵矩形OCMD ,△ODB ,△OCA 的面积为定值,∴四边形OAMB 的面积不会发生变化,∴②正确;连接OM ,当点A 是MC 的中点时,S △OAM=S △OAC .∵S △ODM =S △OCM =a 2,S △ODB =S △OCA ,∴S △OBM =S △OAM .∴S △OBD =S △OBM .∴点B 一定是MD 的中点.∴③正确.二、11.-3 【点拨】设反比例函数的表达式为y =k x ,∵反比例函数的图象经过点(3,1)和(-1,m ),∴k =3×1=-m ,解得m =-3.12.<13.(-1,-2) 【点拨】∵反比例函数y =k x 的图象关于原点成中心对称,一次函数y =mx 的图象经过原点,且关于原点成中心对称,∴它们的交点也关于原点成中心对称.又∵点(1,2)关于原点成中心对称的点为(-1,-2),∴两函数图象的另一个交点的坐标为(-1,-2).14.48<p <12015.y =12x【点拨】连接OA ,则△ABP 与△ABO 的面积相等,都等于6,∴反比例函数的表达式是y =12x .16.12 【点拨】将矩形ABCD 沿x 轴向右平移,当点M 在反比例函数y =1x 的图象上时,过点M 作ME ⊥AB 于点E ,则AE =12AB =32,ME =12BC =12.设OA =m ,则OE =OA +AE =m +32,∴M ⎝ ⎛⎭⎪⎫m +32,12. ∵点M 在反比例函数y =1x 的图象上,∴12=1m +32,解得m =12.17.6 【点拨】∵AC BC =12,△AOB 的面积为6,∴S △AOC =13S △AOB =2.过点A 作AD ⊥y 轴于点D ,如图.则易得△ADC ∽△BOC ,∴DC OC =AC BC =12,∴S △ACD =12S △AOC =1, ∴S △AOD =3.根据反比例函数的比例系数k 的几何意义得12|k |=3,∴|k |=6.∵k >0,∴k =6.18.5;10n n +1【点拨】∵点A 1,A 2在反比例函数y =10x (x >0)的图象上, ∴A 1(2,5),A 2⎝ ⎛⎭⎪⎫4,52, ∴S 1=2×⎝ ⎛⎭⎪⎫5-52=5. 易知A n ⎝ ⎛⎭⎪⎫2n ,5n ,A n +1⎝ ⎛⎭⎪⎫2n +2,5n +1, ∴S n =2×⎝ ⎛⎭⎪⎫5n -5n +1=10n (n +1).∴S 1+S 2+S 3+…+S n =10×⎣⎢⎡⎦⎥⎤12+16+…+1n (n +1)=10×⎝ ⎛⎭⎪⎫1-12+12-13+…+1n -1n +1=10n n +1. 三、19.解:(1)根据题意可得y =600x ,∵y ≤600,∴x ≥1.(2)设实际挖掘了m 天才能完成首期工程,根据题意可得600m -600m +100=0.2,解得m 1=-600(舍去),m 2=500,经检验,m =500是原方程的根.答:实际挖掘了500天才能完成首期工程.20.解:(1)∵OB =2OA =3OD =6,∴OA =3,OD =2,∵CD ⊥OA ,∴DC ∥OB ,易得△AOB ∽△ADC .∴OB CD =AO AD ,∴6CD =35, ∴CD =10,∴点C 的坐标是(-2,10),∵B (0,6),A (3,0),∴⎩⎨⎧b =6,3k +b =0,解得⎩⎨⎧k =-2,b =6, ∴一次函数的表达式为y =-2x +6.∵反比例函数y =m x 的图象经过点C (-2,10),∴m =-20,∴反比例函数的表达式为y =-20x .(2)由⎩⎪⎨⎪⎧y =-2x +6,y =-20x 得⎩⎨⎧x =-2,y =10 或⎩⎨⎧x =5,y =-4.∴点E 的坐标为(5,-4).(3)-2≤x <0或x ≥5.21.解:(1)如图,过点B 作BF ⊥x 轴于点F ,由题意可得BF =6,OF =18.∵四边形OABC 是菱形,∴OC =BC .在Rt △BCF 中,62+(18-BC )2=BC 2,解得BC =10,∴点A 的坐标为(8,6),将点A (8,6)的坐标代入y =k x ,得k =48.(2)由(1)知y =48x ,可设E ⎝ ⎛⎭⎪⎫a ,48a ,如图,过点E 作EG ⊥x 轴于点G ,则OG =a ,EG =48a ,∵EG ⊥x 轴,BF ⊥x 轴,∴EG ∥BF ,易得△OGE ∽△OFB ,∴EG BF =OG OF ,即48a 6=a 18,解得a =12(负值舍去).∴OE OB =OG OF =1218=23,∴OE EB =21=2.22.解:(1)把A (-2,b )的坐标分别代入一次函数和反比例函数的表达式,得⎩⎪⎨⎪⎧b =-2k +5,b =-8-2. 解得⎩⎪⎨⎪⎧b =4,k =12.∴一次函数的表达式为y =12x +5.(2)将直线AB 向下平移m (m >0)个单位长度后,直线AB 对应的函数表达式为y =12x +5-m .由⎩⎪⎨⎪⎧y =-8x ,y =12x +5-m ,得12x 2+(5-m )x +8=0.由题可知Δ=(5-m )2-4×12×8=0,解得m =1或m =9. 23.解:(1)由题意易得点M 的纵坐标为2.将y =2代入y =-12x +3,得x =2.∴M (2,2).把点M 的坐标代入y =k x ,得k =4,∴反比例函数的表达式是y =4x .(2)由题意得S △OPM =12OP ·AM ,∵S 四边形BMON =S 矩形OABC -S △AOM -S △CON =4×2-2-2=4,S △OPM =S 四边形BMON ,∴12OP ·AM =4.又易知AM =2,∴OP =4.∴点P 的坐标是(0,4)或(0,-4).24.解:(1)设y 与x 之间的函数关系式为y =k x ,把x =3,y =400代入y =k x 得,400=k 3,解得k =1 200,∴y 与x 之间的函数关系式为y =1 200x .(2)> 【点拨】把x =6,8,10分别代入y =1 200x 得,y 1=1 2006=200,y 2=1 2008=150,y 3=1 20010=120,∴y 1-y 2=200-150=50,y 2-y 3=150-120=30.∵50>30,∴y 1-y 2>y 2-y 3.25.解:(1)把x =1代入y =x +3,得y =4,∴m =4,∴点A 的坐标为(1,4),∴k =4,则反比例函数的表达式为y =4x .(2)①∵△ABD 的面积为12,A (1,4),∴BD =6,把y =0代入y =x +3,得x =-3,∴点B 的坐标为(-3,0),∴点D 的坐标为(3,0),把x =1,y =4;x =3,y =0分别代入y =nx +b , 得⎩⎨⎧n +b =4,3n +b =0,解得⎩⎨⎧n =-2,b =6.②把x =1,y =4代入y =nx +b 得n +b =4,则b =4-n ,在y =nx +b 中,令y =0,则x =n -4n ,∴点D 的坐标为⎝ ⎛⎭⎪⎫n -4n ,0, 由⎩⎪⎨⎪⎧y =4x ,y =nx +4-n得4x =nx +4-n , 解得x 1=1,x 2=-4n ,∴点E 的坐标为⎝ ⎛⎭⎪⎫-4n ,0, ∴OE =-4n ,∴DE =n -4n -⎝ ⎛⎭⎪⎫-4n =1, ∴t =OE ·DE =-4n ,∴n ·t =-4.。

九上第一章测试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项是正确的?A. 地球自转的方向是自东向西B. 地球自转的方向是自西向东C. 地球公转的方向是自东向西D. 地球公转的方向是自西向东答案:B2. 地球自转一周的时间是多久?A. 24小时B. 12小时C. 48小时D. 36小时答案:A3. 地球公转一周的时间是多久?A. 365天B. 365.25天C. 366天D. 360天答案:B4. 地球自转产生的地理现象是什么?A. 昼夜交替B. 四季更替C. 潮汐现象D. 地壳运动答案:A5. 地球公转产生的地理现象是什么?A. 昼夜交替B. 四季更替C. 潮汐现象D. 地壳运动答案:B二、填空题(每题2分,共20分)1. 地球自转的周期是____小时。
答案:242. 地球公转的周期是____天。
答案:365.253. 地球自转的轴心是____。
答案:地轴4. 地球公转的轨道是____。
答案:椭圆形5. 地球自转产生的地理现象包括____和____。
答案:昼夜交替、时间差异三、简答题(每题10分,共30分)1. 请简述地球自转对人类生活的影响。
答案:地球自转导致昼夜交替,影响人类作息时间,同时产生时间差异,对国际交流和时区划分有重要影响。
2. 请简述地球公转对季节变化的影响。
答案:地球公转使得地球在不同时间接收到的太阳辐射量不同,导致季节变化,如春、夏、秋、冬四季的更替。
3. 请描述地球自转和公转的相互关系。
答案:地球自转和公转是相互独立的运动,但它们共同影响着地球上的气候、季节变化以及昼夜交替等现象。
四、计算题(每题10分,共30分)1. 如果地球自转速度增加,使得自转周期变为12小时,请计算新的昼夜交替周期。
答案:昼夜交替周期将变为12小时。
2. 假设地球公转速度减慢,使得公转周期变为400天,请计算新的一年中季节变化周期。
答案:季节变化周期将变为400天。
3. 假设地球自转轴倾斜角度发生变化,从23.5度变为45度,请分析可能对季节变化的影响。

第一单元测试卷部编版九年级上册(含答案)第一单元测试卷部编版九年级上册一、单选题1.下列诗句朗读节奏划分有误的一项是()A.也许/远水/荡起了一片绿潮B.我看/流云/慢慢地红晕C.叫天风挽/你坦荡地漫游D.像季节/燃起花朵/又把它吹熄2.下列对诗歌的赏析,有误的一项是( )A.诗人未用“珠圆玉润”之类的词语而用“嘶哑”来形容鸟儿鸣唱的歌喉,使人体味到歌者经历的坎坷、悲酸和执着的爱。
B.带“土地”“河流”“风”“黎明”的诗句,抒写了大地遭受的苦难、人民的悲愤以及人民对未来的向往和希冀。
C.“——然后我死了,连羽毛也腐烂在土地里面。
”诗句形象而充分地表达了诗人对土地的眷恋,而且隐含献身之意。
D.“为什么我的眼里常含泪水?因为我对这土地爱得深沉……”诗中的“我”指喻体“鸟”,而不是指诗人自己。
3.下面语段中加点字的注音完全正确的一项是()天翻地覆慨而慷。
今天,天安门广场铁流浩荡,宣告当代中国军人捍卫祖国主权、维护祖国统一的坚强意志,展示震撼世界、蓬勃向上的“中国力量”!A.lǚdàng gàn hànB.lǚshāng hàn gànC.fùshāng gàn gànD.fùdàng hàn hàn4.下列句子运用的修辞手法与其他三项不同的一项是()A.人间四月天,清丽典雅地涉水而来,清清浅浅,让你尽展笑颜。
B.为了迎接四月,大地做了隆重的准备。
C.四月的风恣意地亲吻着我们的脸,轻轻摇曳着我们的心。
D.你是四月早天里的云烟。
5.下列对《我爱这土地》这首诗的赏析不恰当的一项是()A.诗人假设自己是一只鸟,一只“用嘶哑的喉咙歌唱”的鸟,是为了借鸟歌唱的内容更好地抒情。
B.关于“土地”“河流”“风”“黎明”的一组诗句,抒写了祖国遭受的苦难、人民的悲愤和激怒、对光明的向往和希冀。
C.“——然后我死了,/连羽毛也腐烂在土地里面”这两句诗形象而充分地表达了诗人对土地的眷恋,而且隐含献身之意。

教科版】初三九年级物理上册《第一章达标检测卷》(附答案)第一章达标检测卷一、选择题(每题3分,共36分)1.春天,走在农业生态园的树荫道上,阵阵花香扑鼻,这是由于()A。
分子的无规则运动B。
分子间有空隙C。
分子间的吸引力D。
分子间的斥力答案:C解析:花香扑鼻是因为花中的分子散发到空气中,分子间的吸引力使得这些分子聚集在一起,形成花香。
2.美丽的泉城济南,山清水秀、景色宜人。
以下泉城美景的形成,与“分子动理论”有关的是()A。
趵突泉,泉水清澈见底B。
千佛山,寺内暮鼓晨钟C。
大明湖,湖面荷花飘香D。
植物园,处处花团锦簇答案:A解析:趵突泉的泉水清澈见底是由于水分子间的吸引力,使得泉水中的杂质分子被过滤掉,只有水分子透过泉眼喷出。
3.南极是世界上最冷的地方之一,常年平均气温约-25℃,一天,企鹅妈妈与小企鹅之间发生了一次有趣的对话,它们的部分说法如下,其中正确的是()A。
小企鹅:妈妈,这么冷,我都没温度了B。
企鹅妈妈:不对,是没有内能C。
小企鹅:冰天雪地的,连水蒸气都没有D。
企鹅妈妈:呵呵,水蒸气倒肯定有,因为冰可以升华呀答案:B解析:内能是物体分子间的运动能、势能和内部结构能的总和,与温度有关,而不是与热量有关。
4.关于温度、热量和内能,以下说法正确的是()A。
物体的温度升高,内能一定增加B。
60℃的水比30℃的水所含有的热量多C。
热量总是自发地从温度低的物体向温度高的物体传递D。
0℃的水内能为零答案:A解析:温度是物体内部分子运动的平均能量,温度升高表示分子运动更加剧烈,内能也随之增加。
5.2015年5月26日印度出现高温天气,首都新德里的一条道路上的沥青被烤化,斑马线变得扭曲模糊,如图所示。
关于这个情景的说法正确的是()答案:C解析:沥青被烤化是由于受到高温的影响,分子间的热运动增强,分子间的吸引力减弱,导致沥青分子间的结构松散,变得软化。
6.下列实例中,通过热传递的方式来改变物体内能的是()A。

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第一章单元综合测试一、单选题1.已知四边形ABCD 是平行四边形,AC ,BD 相交于点O ,下列结论错误的是( ) A .OA OC =,OB OD =B .当AB CD =时,四边形ABCD 是菱形C .当90ABC ∠=︒时,四边形ABCD 是矩形D .当AC BD =且AC BD ⊥时,四边形ABCD 是正方形2.如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,8AC =,6BD =,点E 是CD 上一点,连接OE ,若OE CE =,则OE 的长是( )A .2B .52C .3D .4 3.如图,面积为S 的菱形ABCD 中,点O 为对角线的交点,点E 是线段BC 单位中点,过点E 作EF BD ⊥于F ,EG AC ⊥与G ,则四边形EFOG 的面积为( )A .14SB .18SC .112S D .116S 4.如图,菱形ABCD 中,对角线AC ,BD 相交于点O ,E 为AB 的中点.若菱形ABCD 的周长为32,则OE 的长为( )A .3B .4C .5D .65.如图,正方形ABCD 的面积为1,M 是AB 的中点,则图中阴影部分的面积是( )A .310B .13C .25D .496.如图,正方形ABCD 的边长8AB =,E 为平面内一动点,且4AE =,F 为CD 上一点,2CF =,连接EF ,ED ,则2EF ED +的最小值为( )A .B .C .12D .10二、填空题7.如图,在菱形ABCD 中,50B ∠=︒,点E 在CD 上,若AE AC =,则BAE ∠=________.8.如图,在矩形ABCD 中,E ,F 分别为边AB ,AD 的中点,BF 与EC ,ED 分别交于点M ,N .已知4AB =,6BC =,则MN 的长为________.9.如图,在矩形ABCD 中,9AB =,AD =,点P 是边BC 上的动点(点P 不与点B ,点C 重合),过点P 作直线PQ BD ∥,交CD 边于Q 点,再把PQC △沿着动直线PQ 对折,点C 的对应点是R 点,则CQP ∠=________.10.如图,正方形ABCD 中,点E 为对角线AC 上一点,且AE AB =,则BEA ∠的度数是________度.三、作图题11.在正方形ABCD 中,E 是CD 边上的点,过点E 作EF BD ⊥于F .(1)尺规作图:在图中求作点E ,使得EF EC =;(保留作图痕迹,不写作法) (2)在(1)的条件下,连接FC ,求BCF ∠的度数.四、综合题12.如图,ABCD 的对角线AC ,BD 相交于点O ,过点O 作EF AC ⊥,分别交AB ,DC 于点E 、F ,连接AF 、CE .(1)若32OE =,求EF 的长;(2)判断四边形AECF 的形状,并说明理由.13.如图,在ABC △中,AB AC =,点D 、E 分别是线段BC 、AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF .(1)求证:A BDE F E △≌△;(2)求证:四边形ADCF 为矩形.14.如图,四边形ABCD 的对角线AC ,BD 交于点O ,过点D 作DE BC ⊥于E ,延长CB 到点F ,使BF CE =,连接AF ,OF .(1)求证:四边形AFED 是矩形;(2)若7AD =,2BE =,45ABF ∠=︒,试求OF 的长.15.如图,点E 是正方形ABCD 外一点,点F 是线段AE 上一点,且EBF △是等腰直角三角形,其中90EBF ∠=︒,连接CE 、CF(1)求证:ABF CBE △≌△;(2)判断CE 与EF 的位置关系,并说明理由.16.如图,菱形EFGH 的三个顶点E 、G 、H 分别在正方形ABCD 的边AB 、CD 、DA 上,连接CF .(1)求证:HEA CGF ∠∠=;(2)当AH DG =时,求证:菱形EFGH 为正方形.第一章单元综合测试答案解析一、 1.【答案】B【解析】∵四边形ABCD 是平行四边形,OA OC =∴,OB OD =,故A 正确,∵四边形ABCD 是平行四边形,AB CD =,不能推出四边形ABCD 是菱形,故B 错误,∵四边形ABCD 是平行四边形,90ABC ∠=︒, ∴四边形ABCD 是矩形,故C 正确,∵四边形ABCD 是平行四边形,AC BD =,AC BD ⊥, ∵四边形ABCD 是正方形.故D 正确.故答案为:B . 2.【答案】B【解析】∵四边形ABCD 是菱形,8AC =,6BD =,142CO AC ==∴,132OD BD ==,AC BD ⊥,5DC =∴,90EOC DOE ∠+∠=︒,90DCO ODC ∠+∠=︒,OE CE =∵,EOC ECO ∠=∠∴,DOE ODC ∠=∠∴,DE OE =∴,1522OE CD ==∴故答案为:B . 3.【答案】B【解析】∵四边形ABCD 是菱形,OA OC =∴,OB OD =,AC BD ⊥,12S AC BD =⨯, EF BD ⊥∵于F ,EG AC ⊥于G ,∴四边形EFOG 是矩形,EF OC ∥,EG OB ∥,∵点E 是线段BC 的中点,EF ∴、EG 都是OBC △的中位线,1124EF OC AC ==∴,1124EG OB BD ==,∴矩形EFOG 的面积11111=44828EF EG AC BD AC BD S ⎛⎫=⨯=⨯=⨯⨯ ⎪⎝⎭;故答案为:B . 4.【答案】B【解析】∵四边形ABCD 是菱形,AC BD ⊥∴,AB BC CD AD ===, 90AOB ∠=︒∴,又32AB BC CD AD +++=∵.8AB =∴,在Rt AOB △中,OE 是斜边上的中线,142OE AB ==∴. 故答案为:B . 5.【答案】B【解析】如图,过点E 作HF AB ⊥,AM CD ∵∥,DCE EAM ∠=∠∴,CDE EMA ∠=∠,AME CDE △∽△∴,::1:2AM DC EH EF ==∴,1FH AD ==,13EH =∴,23EF =.∴阴影部分的面积1111112343ABCD AME CDE M BC S S S S =−−−=−−−=△△△正方形. 故答案为:B . 6.【答案】B【解析】如图,在AD 上取点k ,使2AK =,连接EK ,在AEK △和ADE △中,EAK DAE ∠=∠,AEK ADE △∽△∴,12EK AE ED AD ==∴,即12EK ED =,12EF ED EF EK +=+∴,当F 、E 、K三点共线时,21EF ED FK +== ()1222()EF ED EF ED +=+=最小∴,故答案为:B 。

九年级数学上册第一章测试题及答案_证明(二)(B)第一篇:九年级数学上册第一章测试题及答案_证明(二)(B) 北九上第一章证明(二)水平测试(B)一、选择题(本大题有10小题,每小题3分,共30分.请选出每小题中一个符合题意的正确选项,不选、多选、错选,均不给分)1.两个直角三角形全等的条件是()(A)一锐角对应相等;(B)两锐角对应相等;(C)一条边对应相等;(D)两条边对应相等.2.到∆ABC的三个顶点距离相等的点是∆ABC的().(A)三边垂直平分线的交点;(B)三条角平分线的交点;(C)三条高的交点;(D)三边中线的交点.(第3题)3.如图,由∠1=∠2,得∆ABC≌∆EDCBC=DC,AC=EC,的根据是()(A)SAS(B)ASA(C)AAS(D)SSS4.∆ABC中,AB=AC,BD平分∠ABC交AC边于点D,∠BDC=75,则∠A的度数为()(A)35°(B)40°(C)70°(D)110°5.下列两个三角形中,一定全等的是()(A)有一个角是40°,腰相等的两个等腰三角形;B(B)两个等边三角形;A(C)有一个角是100°,底相等的两个等腰三角形;(第7题)(D)有一条边相等,有一个内角相等的两个等腰三角形.6.适合条件∠A=∠B =∠C的三角形一定是()(A)锐角三角形;(B)钝角三角形;(C)直角三角形;(D)任意三角形.7.有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A 处树立一个标牌“少走▇米,踏之何忍?”请你计算后帮小明在标牌的“▇”填上适当的数字是().(A)3米(B)4米(C)5米(D)6米8.一个三角形如果有两边的垂直平分线的交点在第三边上,那么这个三角形是().(A)等腰三角形;(B)等边三角形;(C)直角三角形;(D)等腰直角三角形.9.如图,已知AC平分∠PAQ,点B、B'分别在边AP、AQ上,如果(第9题)ο13添加一个条件,即可推出AB=AB',那么该条件不可以是()(A)BB'⊥AC(B)BC=B'C(C)∠ACB=∠ACB'(D)∠ABC =∠AB'C10.如图,FD⊥AO于D,FE⊥BO于E,下列条件:①OF是∠AOB的平分线;②DF=EF;③DO=EO;④∠OFD=∠OFE.其中能够证明∆DOF≌∆EOF的条件的个数有()(第10题)(A)1个(B)2个(C)3个(D)4个二、填空题(本大题有10小题,每小题3分,共30分.将答案填在题中横线上)11.在∆ABC中,边AB、BC、AC的垂直平分线相交于P,则PA、PB、PC的大小关系是.12.如果等腰三角形的一个角是80°,那么顶角是度.13.若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为.14.∆ABC中,∠C=90,AD平分∠BAC,交BC于点D,若οDC=7,则D到AB的距离是.15.如图,∠ABC=∠DCB,需要补充一个直接条件才能使∆ABC(第15题)≌∆DCB.甲、乙、丙、丁四位同学填写的条件分别是:甲“AB=DC”;乙“AC=DB”;丙“∠A=∠D”;丁“∠ACB=∠DBC”.那么这四位同学填写错误的是.16.用反证法证明“三角形中至少有一个角不小于60°时,假设“”,则与“”矛盾,所以原命题正确.17.补全“求作∠AOB的平分线”的作法:①在OA和OB上分别截取OD、OE,使OD=OE.②分别以D、E为圆心,以为半径画弧,两弧在∠AOB内交于点C.③作射线OC即为∠AOB的平分线.18.一轮船以每小时20海里的速度沿正东方向航行.上午8时,该船在A 处测得某灯塔位于它的北偏东30°的B处(如图),上午9时行到C 处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是海里(结果保留根号).19.在∆ABC中,∠A=90°,AB=AC,BD平分∠B交AC于D,(第18题)DE⊥BC于E,若BC=10,则∆DEC的周长是20.如图是2002年8月在北京召开的第24届国际数学家大会的会标,它是由4个相同的直角三角形拼和而成.若图中大小正方形的面积分别为52cm和4cm,则直角三角形的两条直角边的和是cm.三、解答题(本大题有6小题,共60分.解答需写出必要的文字说明、演算步骤或证明过程)21.(8分)已知:如图,OB=OC.∠A=∠D=90,AC=BD.求证:26.(12分)已知:如图,点C为线段AB上一点,∆ACM、∆CBN是等边三角形,可以说明:∆ACN≌∆MCB,从而得到结论:AN=BM.现要求:(1)将∆ACM绕C点按逆时针方向旋转180°,使A点落在CB 上.请对照原题图在下图中画出符合要求的图形(不写作法,保留作图痕迹).(2)在(1)所得到的图形中,结论“AN=BM”是否还成立?若成立,请给予证明;若不成立,请说明理由.(3)在(1)所得到的图形中,设MA的延长线与BN相交于D 点,请你判断△ABD与四边形MDNC的形状,并说明你的结论的正确性.NA C B第二篇:初三数学《证明二》测试题初三数学《证明二》测试题一、选择题(每小题3分,共30分)1、两个直角三角形全等的条件是()A、一锐角对应相等B、两锐角对应相等C、一条边对应相等D、两条边对应相等2、如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是()A、SASB、ASAC、AASD、SSS3、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在()7、如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=12cm,则△DEB的周长()A、6cmB、8cmC、12cmD、24cm8、如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m 和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是()A.2mB.3mC.6mD.9m9、如图,已知AC平分∠PAQ,点B,B′分别在边AP,AQ上,如果添加一个条件,即可推出AB=AB′,那么该条件可以是()A、BB′⊥ACB、BC=B′CC、∠ACB=∠ACBD、∠ABC=∠AB′C10、如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AEA.△ABC 的三条中线的交点B.△ABC 三边的中垂线的交点C.△ABC 三条角平分线的交点D.△ABC与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,其中正确结论的个数()4.如图所示,AB = AC,要说明△ADC≌△AEB不能是(..BE)A.∠B =∠CB.AD = AEC.∠ADC=∠AEBD.DC =A.1个B.2个C.3个D.4个二、填空题(每小题3分,共30分)1、如果等腰三角形的一个角是80°,那么顶角是().2、等腰三角形的两个底角相等的逆命题是().3、等腰三角形一腰上的中线把等腰三角形周长分为15cm和12cm的两部分,则底边长为().5、如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=10,AC=5,则图中等于60°的角的个数为()A、2B、3C、4D、56、如图所示的正方形网格中,网格线的交点称为格点.已知A、B两格点,如果C也是图中的格点,且使得 ABC为等腰三角形,则.....C的个数是()A.6是点4、如图,点F、C在线段BE上,且∠1=∠2,BC=EF,若要使△ABC≌△DEF,则还须补充一个条件()5、如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC。

第一章达标检测卷一、选择题(每题3分,共30分)1.菱形、矩形、正方形都具有的性质是()A.四条边相等,四个角相等B.对角线相等C.对角线互相垂直D.对角线互相平分2.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于() A.20 B.15 C.10 D.53.如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD面积的()A.15 B.14 C.13 D.3104.如图,菱形ABCD的周长为24 cm,对角线AC,BD相交于点O,点E是AD 的中点,连接OE,则线段OE的长等于()A.3 cm B.4 cm C.2.5 cm D.2 cm5.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为()A.3 B.2 2 C. 6 D.3 36.顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形7.如图,把一张长方形纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()A.15°或30°B.30°或45°C.45°或60°D.30°或60°8.如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F,且E,F分别为BC,CD的中点,则∠EAF等于()A.75°B.45°C.60°D.30°9.如图,在矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是()A.AF=AE B.△ABE≌△AGF C.EF=2 5 D.AF=EF10.如图,在正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①BE=DF;②∠DAF=15°;③AC 垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE.其中正确结论有() A.2个B.3个C.4个D.5个二、填空题(每题3分,共24分)11.如图是一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α的度数为________时,两条对角线长度相等.12.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边的正方形ACEF 的周长为________.13.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC∶∠EDA=1∶2,且AC=10,则EC的长度是________.14.如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为________.15.菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0,3),动点P从点A出发,沿A→B→C→D→A→B→……的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2 023 s时,点P的坐标为________.16.如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y-4)2的值为________.17.如图,在矩形ABCD中,AB=3,BC=2,点E为AD的中点,点F为BC 边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG +FH=________.18.如图,在Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形的对角线交于点O,连接O C.已知AC=5,OC=62,则另一直角边BC的长为________.三、解答题(19,20题每题9分,21题10分,22,23题每题12分,24题14分,共66分)19.如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于点E,DF⊥BC交BC的延长线于点F.求证:DE=DF.20.如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD,过点D作DE∥AC,CE与DE相交于点E.(1)求证:四边形OCED是矩形;(2)若AB=4,∠ABC=60°,求矩形OCED的面积.21.如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.(1)求证:BD=BE;(2)若BE=10,CE=6,连接OE,求△ODE的面积.22.如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.(1)求证:△DCE≌△BFE;(2)若CD=2,∠ADB=30°,求BE的长.23.如图,在菱形ABCD中,AB=4,∠BAD=120°,以点A为顶点的一个60°的∠EAF绕点A旋转,∠EAF的两边分别交BC,CD于点E,F,且E,F 不与B,C,D重合,连接EF.(1)求证:BE=CF.(2)在∠EAF绕点A旋转的过程中,四边形AECF的面积是否发生变化?如果不变,求出其定值;如果变化,请说明理由.24.在正方形ABCD的外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)依题意补全图①;(2)若∠P AB=20°,求∠ADF的度数;(3)如图②,若45°<∠P AB<90°,用等式表示线段AB,EF,FD之间的数量关系,并给出证明.答案一、1.D 2.B 3.B4.A点拨:∵菱形ABCD的周长为24 cm,∴AB=24÷4=6 (cm),OB=OD.又∵E为AD的中点,∴OE是△ABD的中位线.∴OE=12AB=12×6=3 (cm).故选A.5.D 6.D7.D8.C9.D点拨:如图,由折叠的性质得∠1=∠2.∵AD∥BC,∴∠3=∠1.∴∠2=∠3.∴AE=AF.故选项A正确.由折叠的性质得CD=AG,∠D=∠G=90°.∵AB=CD,∴AB=AG.又∵AE=AF,∠B=90°,∴Rt△ABE≌Rt△AGF(HL).故选项B正确.设DF=x,则GF=x,AF=8-x.又∵AG=AB=4,∴在Rt△AGF中,根据勾股定理得(8-x)2=42+x2. 解得x=3.∴AF=8-x=5.则AE=AF=5,∴BE =AE 2-AB 2=52-42=3.过点F 作FM ⊥BC 于点M ,则FM =4,EM =5-3=2.在Rt △EFM 中,根据勾股定理得EF =EM 2+FM 2=22+42=20=25,则选项C 正确.∵AF =5,EF =25,∴AF ≠EF .故选项D 错误. 10.C 点拨:∵四边形ABCD 是正方形, ∴AB =BC =CD =AD ,∠B =∠BCD =∠D =∠BAD =90°. ∵△AEF 是等边三角形, ∴AE =EF =AF ,∠EAF =60°. ∴∠BAE +∠DAF =30°.在Rt △ABE 和Rt △ADF 中,⎩⎨⎧AE =AF ,AB =AD ,∴Rt △ABE ≌Rt △ADF (HL ). ∴BE =DF (故①正确), ∠BAE =∠DAF .∴∠DAF +∠DAF =30°,即∠DAF =15°(故②正确). ∵BC =CD ,∴BC -BE =CD -DF ,即CE =CF , 又∵AE =AF ,∴AC 垂直平分EF (故③正确).设EC =x ,由勾股定理,得EF =AE =2x ,∴EG =CG =22x .∴AG =62x . ∴AC =6x +2x2. ∴AB =BC =3x +x 2.∴BE =3x +x 2-x =3x -x2.∴BE +DF =3x -x ≠2x (故④错误).易知S △CEF =x 22,S △ABE=3x -x 2·3x +x 22=x 24,∴2S △ABE =x 22=S △CEF (故⑤正确).综上所述,正确的有4个. 二、11.90° 12.16 13.2.514.213 点拨:设正方形的边长为a ,∵S △ABE =18, ∴S 正方形ABCD =2S △ABE =36, ∴a 2=36.∵a >0,∴a =6. 在Rt △BCE 中,∵BC =6,CE =4,∠C =90°, ∴BE =BC 2+CE 2=62+42=213. 15.⎝ ⎛⎭⎪⎫-34,34 16.16 点拨:∵四边形ABCD 是矩形,AB =x ,AD =y ,∴CD =AB =x ,BC =AD =y ,∠BCD =90°.又∵BD ⊥DE ,点F 是BE 的中点,DF =4,∴BF =DF =EF =4,∴CF =4-BC =4-y .在Rt △DCF 中,DC 2+CF 2=DF 2,即x 2+(4-y )2=42=16.∴x 2+(y -4)2=16. 17.3105 点拨:如图,连接EF ,∵四边形ABCD 是矩形, ∴CD =AB =3,AD =BC =2, ∠A =∠D =90°.∵点E 为AD 的中点,∴AE =DE =1,∴BE =AE 2+AB 2=12+32=10,CE =DE 2+DC 2=12+32=10, ∴CE =BE .∵S △BCE =S △BEF +S △CEF ,∴12BC·AB=12BE·FG+12CE·FH,∴BC·AB=BE(FG+FH),即2×3=10(FG+FH),解得FG+FH=310 5.18.7点拨:如图,过点O作OM⊥CA,交CA的延长线于点M,过点O作ON⊥BC于点N,易证△OMA≌△ONB,CN=OM,∴OM=ON,MA=NB.又∵∠ACB=90°,∠OMA=∠ONB=90°,OM=ON,∴四边形OMCN是正方形.∴△OCM为等腰直角三角形.∵OC=62,∴CM=OM=6.∴MA=CM-AC=6-5=1.∴BC=CN+NB=OM+MA=6+1=7.故答案为7.三、19.证明:连接DB.∵四边形ABCD是菱形,∴BD平分∠ABC.又∵DE⊥AB,DF⊥BC,∴DE=DF.20.(1)证明:∵CE∥OD,DE∥AC,∴四边形OCED是平行四边形.又∵四边形ABCD是菱形,∴AC⊥BD,即∠COD=90°,∴四边形OCED是矩形.(2)解:∵在菱形ABCD中,AB=4,∴AB=BC=CD=4.又∵∠ABC=60°,∴△ABC是等边三角形,∴AC=4,∴OC=12AC=2,∴OD=42-22=23,∴矩形OCED的面积是23×2=4 3.21.(1)证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD.又∵BE∥AC,E在DC的延长线上.∴四边形ABEC是平行四边形,∴AC=BE,∴BD=BE.(2)解:如图,过点O作OF⊥CD于点F.∵四边形ABCD是矩形,∴∠BCD=90°,∴∠BCE=90°.在Rt△BCE中,根据勾股定理可得BC=8.∵BE=BD,∠BCD=90°,∴CD=CE=6,∴DE=12.∵OD=OC,OF⊥CD,∴CF=DF.又OB=OD,∴OF为△BCD的中位线,∴OF=12BC=4,∴S △ODE =12DE ·OF =12×12×4=24.22.(1)证明:∵在矩形ABCD 中,AD ∥BC ,∠A =∠C =90°,∴∠ADB =∠DBC .根据折叠的性质得∠ADB =∠FDB ,∠F =∠A =90°,∴∠DBC =∠FDB ,∠C =∠F .∴BE =DE .在△DCE 和△BFE 中,⎩⎨⎧∠DEC =∠BEF ,∠C =∠F ,DE =BE ,∴△DCE ≌△BFE .(2)解:在Rt △BCD 中,∵CD =2,∠DBC =∠ADB =30°,∴BD =4.∴BC =2 3.在Rt △ECD 中,易得∠EDC =30°.∴DE =2EC .∴(2EC )2-EC 2=CD 2.又∵CD =2,∴CE =233.∴BE =BC -EC =433.23.(1)证明:如图,连接AC .∵四边形ABCD 为菱形,∠BAD =120°,∴AB =BC =CD =DA ,∠BAC =∠DAC =60°,∴△ABC 和△ADC 都是等边三角形,∴∠ABE =∠ACF =60°,AB =AC ,∠1+∠2=60°.∵∠3+∠2=∠EAF =60°,∴∠1=∠3.∴△ABE ≌△ACF .∴BE =CF .(2)解:四边形AECF 的面积不变.由(1)知△ABE ≌△ACF ,则S △ABE =S △ACF ,故S 四边形AECF =S △AEC +S △ACF =S △AEC +S △ABE =S △ABC .如图,过点A 作AM ⊥BC 于点M ,则BM =MC =2,∴AM =AB 2-BM 2=42-22=2 3.∴S △ABC =12BC ·AM =12×4×23=4 3.故S 四边形AECF =4 3.24.解:(1)如图①.(2)如图②,连接AE ,∵点E 是点B 关于直线AP 的对称点,∴∠P AE =∠P AB =20°,AE =AB .∵四边形ABCD 是正方形,∴AE =AB =AD ,∠BAD =90°.∴∠AED =∠ADE ,∠EAD =∠DAB +∠BAP +∠P AE =130°.∴∠ADF =180°-130°2=25°. (3)EF 2+FD 2=2AB 2.证明如下:如图③,连接AE ,BF ,BD ,由轴对称和正方形的性质可得,EF =BF ,AE =AB =AD ,易得∠ABF =∠AEF =∠ADF .∵∠BAD =90°,∴∠ABF +∠FBD +∠ADB =90°.∴∠ADF +∠ADB +∠FBD =90°.∴∠BFD =90°.在Rt △BFD 中,由勾股定理得BF 2+FD 2=BD 2.在Rt △ABD 中,由勾股定理得BD 2=AB 2+AD 2=2AB 2,∴EF 2+FD 2=2AB 2.。

九年级上册数学第一单元测试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个正方形的边长为a,则它的对角线长为()A. a/2B. a√2C. 2aD. a²2. 下列函数中,哪一个不是正比例函数?()A. y = 3xB. y = x/2C. y = 5D. y = 2x + 13. 已知一组数据:2, 5, 7, 10, 12,这组数据的中位数是()A. 5B. 7C. 10D. 24. 在直角坐标系中,点(3, 4)关于x轴的对称点是()A. (3, -4)B. (-3, 4)C. (4, 3)D. (-3, -4)5. 若两个角互为补角,且其中一个角为60度,则另一个角为()A. 30度B. 90度C. 120度D. 180度二、判断题(每题1分,共5分)6. 任何两个锐角的和一定是钝角。
()7. 一组数据的平均数总是大于等于它的中位数。
()8. 两条平行线的同位角相等。
()9. 任何正方形的对角线都相等。
()10. 一元二次方程的解可以是两个相等的实数根。
()三、填空题(每题1分,共5分)11. 若一个三角形的两边长分别为3cm和4cm,且这两边的夹角为90度,则第三边的长为____cm。
12. 函数y = 2x + 1的图像是一条____。
13. 若一个数的平方根是9,则这个数是____。
14. 在直角坐标系中,点(0, b)在____轴上。
15. 若一个等腰三角形的底边长为10cm,腰长为13cm,则这个三角形的周长为____cm。
四、简答题(每题2分,共10分)16. 简述正比例函数的定义。
17. 解释什么是等腰三角形,并给出一个等腰三角形的例子。
18. 描述一次函数图像的特点。
19. 什么是中位数?如何计算一组数据的中位数?20. 解释补角的概念,并给出一个例子。
五、应用题(每题2分,共10分)21. 一个长方形的周长为18cm,长为7cm,求宽。

九年级上册第一章第1-2节章节测试(一)相对原子质量:H-1 O-16 Al-27 S-32 Cl-35.5 Cu-64 Zn-65一、选择题1、“物理变化和化学变化的区分”是中考经常要考查的一个重要知识点,以下有关区分二者的依据的说法中,你认可的是()①是否生成其他物质;②是否有明显的现象;③构成物质的分子是否发生改变;④是否放出热量。
A、①②③B、②④C、①③D、①④2、水冷却后,除了会凝固成冰晶体外,还会形成玻璃态,它是由液态水急速冷却到-108°C时形成的,玻璃态的水与普通液态水的密度相同,下列说法正确的是()A、水由液态变为玻璃态,体积减小B、水由液态变为玻璃态,体积膨胀C、水由液态变为玻璃态是物理变化D、水由液态变为玻璃态是化学变化3、含有下列各组离子的溶液,其中的溶质都属于酸的是()A、Na+ H+SO42-B、Ca2+OH-Na+C、H+SO42-Cl-D、K+CO32-NO3-4、咖喱是一种烹饪辅料,若白衬衫被咖啡沾污后,用普通肥皂洗涤该污渍时,黄色污渍会变成红色,经水漂洗后,红色又变为黄色。
据此现象,你认为咖喱汁与下列何种试剂可能具有相似的化学作用()A. 硫酸溶液B. 石灰水C. 石蕊试液D. 碘酒5、向某溶液中滴入无色酚酞溶液后不显色,向该溶液中滴入紫色石蕊溶液,则()A、一定显红色B、可能仍为紫色,也可能显红色C、可能显蓝色D、一定显无色6、对下列实验过程的评价正确的是()A、烧碱溶液中是否混有氯化钠,可先加稀盐酸,再加硝酸银溶液即可B、某溶液中滴加氯化钡溶液,生成不溶于稀硝酸的白色沉淀,该溶液中一定含有SO42-C、某无色溶液中滴入酚酞试液变红色,该溶液一定是碱溶液D、回收废旧金属,既可以节约资源,又可以防止环境污染7、下列物质长期暴露在潮湿的空气中,质量会增加且没有变质的是()A、烧碱固体B、浓盐酸C、浓硫酸D、生铁8、下列不属于稀盐酸与稀硫酸共有的化学性质是()A.能与碳酸钠反应放出二氧化碳B.能与锌反应放出氢气C.能与氯化钡溶液反应产生白色沉淀D.能与氢氧化铁反应生成有色溶液9、下列关于盐酸的用途中,不能用稀硫酸代替的是()A、制氢气B、除铁锈C、制二氧化碳D、溶解氧化铜10、用酸A跟足量的碳酸钠固体反应,并将生成的气体通入澄清石灰水中,在较长一段时间内未发现石灰水变浑浊,则酸A是()A、浓硫酸B、稀硫酸C、磷酸D、浓盐酸11、证明木炭粉中是否混有氧化铜,某兴趣小组设计了以下四种方案,其中可行的是()A、在样品中加氢氧化钠溶液,观察粉末是否会减少B、在样品中加稀硫酸,充分反应后过滤,观察滤液是否呈蓝色C、在空气中加热样品,恢复至原温度后,称量固体质量是否减少D、在样品中加水,观察是否有蓝色沉淀12、除去下列各组物质中的杂质(括号内为杂质),不能用稀盐酸的是()A、Cu(Fe)B、NaCl溶液(Na2CO3)C、CaO(CaCO3)D、稀HNO3(AgNO3)13、氯化钙溶液中含有少量盐酸杂质,在没有指示剂又不能增加其他杂质的情况下除去杂质,最好选用()A、石灰石B、烧碱C、碳酸钠D、熟石灰14、在家中可用来洗涤热水瓶内的少量水垢的物质是()A、稀盐酸B、食醋C、洗衣粉D、食盐水15、下列溶液中,能跟稀盐酸反应产生白色沉淀的是()A、NaCl溶液B、Ca(OH)2溶液C、AgNO3溶液D、H2SO4溶液16、若鉴定某无色溶液是盐酸应选用的试剂有()A、紫色石蕊试液B、硝酸银溶液和稀硝酸C、无色酚酞试液和硝酸银溶液D、紫色石蕊试液,硝酸银溶液和稀硝酸17、汽车、电动车一般使用的是铅酸蓄电池,某铅酸蓄电池用的是28%的稀硫酸,现用1.0kg 98%的浓硫酸配制该稀硫酸.下列说法中正确的是()A、28%的稀硫酸中溶质与溶剂的质量比为28:100B、用l.0kg98%的浓硫酸可配制3.5kg28%的稀硫酸C、配制该稀硫酸时,把水沿容器内壁缓慢注入浓硫酸中D、配制好的稀硫酸可以存放在铁制容器中18、向盛有酚酞和NaOH溶液的烧杯中滴加稀硫酸,直至液体呈无色。

第一章综合测试答案解析一、1.【答案】C【解析】小小秤砣压千斤,是利用杠杆的动力臂远大于阻力臂进行称量的,所以此时杆秤不是等臂杠杆,故A错误;摘不到的是镜中花,镜中花属于平面镜成像,是由于光的反射形成的,故B错误;墙内开花墙外香,是花的香味分子做无规则运动的结果,属于扩散现象,故C正确;化雪冷,是因为雪在熔化时吸热,使气温降低,故D错误。
2.【答案】B3.【答案】B【解析】用塑料泡沫箱可长时间保存冰冻食品,是因为塑料泡沫的隔热性能比较好,能够隔绝大部分的热量,即导热性差,故ACD不符合题意,B符合题意。
故选B。
4.【答案】A【解析】热传递过程中传递的是热量,不是温度,温度是状态量,不能传递,故A错误;同一物体分子个数是一定的,当温度降低时,分子的热运动越缓慢,则分子的动能就越小,从而物体的内能减小,由于铁块的质量不变,因此铁块的温度降低,内能一定减小,故B正确;晶体在熔化过程继续吸热,但温度不变,故C正确;物体温度升高,可能吸收了热量,也可能是对它做了功,故D正确。
5.【答案】C6.【答案】C7.【答案】A8.【答案】D【解析】A、B、C项,均是利用热传递改变了物体的内能。
D项,用手反复弯折铁丝,弯折处铁丝的温度升高,是手对铁丝做了功,属于做功改变物体的内能。
9.【答案】D10.【答案】A二、11.【答案】温度(其他写法合理均可)12.【答案】不良导体热传导对流热传导热辐射13.【答案】分子间隙越大14.【答案】相等相等煤油不同15.【答案】焦耳质量种类升高的温度16.【答案】热传递做功17.【答案】加快增大减慢减小体积分子势能增大状态18.【答案】分子原子【解析】常见的物质是由分子、原子构成的。
三、19.【答案】(1)蒸发吸热【解析】无电“冰箱”,是利用沙子中的水蒸发吸收热量,使内桶中食物的温度不致太高。
所以其基本原理是蒸发吸热。
(2)金属的导热性好【解析】金属具有良好的导热性能,内桶采用金属材料,可以将食物热量迅速传递到沙子。
教科版九年级物理上册第一章达标测试卷一、选择题(每题3分,共36分)1.下列选项中不能用分子热运动理论解释的是()A.酒香不怕巷子深B.炒菜时放盐使菜变咸C.环境恶化尘土满天飞D.教室喷清新剂,香气四溢2.关于分子热运动及热现象,下列说法正确的是()A.固体很难被压缩,说明分子间存在斥力B.扩散现象只能发生在气体与液体中C.物体吸收热量,温度一定升高D.-20 ℃的冰块没有内能3.下列实例中,通过做功方式改变物体内能的是()A.阳光晒热棉被B.锯木头时锯条变热C.用热水袋取暖D.冷气使房间温度降低4.【新题】第七届山东省花博会于2020年9月29日在青州盛大开幕!步入展厅,花开烂漫,满厅清香。
“满厅清香”体现的物理知识是()A.物质是由分子组成的B.分子之间存在着空隙C.分子间存在力的作用D.分子永不停息地运动5.水具有比热容大的特点,图中的现象中与此特点无关的是()6.小李喜欢喝咖啡,冲调咖啡时总能闻到浓浓的香味,以下关于咖啡的说法不正确的是()A.咖啡在变冷的过程中,内能不断增加B.咖啡在变冷的过程中,以热传递的方式改变了内能C.咖啡香飘四溢是扩散现象,说明分子在运动D.咖啡温度越高,分子的热运动越剧烈7.以下说法中正确的是()A.物体的机械能和物体的内能是同种形式的能,都与物体的机械运动和分子热运动以及分子间的相互作用情况有关B.固体很难被压缩,说明分子之间只存在斥力C.分子之间存在着相互作用的引力和斥力D.扩散现象只能说明分子是运动的,不能说明分子之间存在空隙8.下列关于分子动理论与内能,说法正确的是()A.甲物体传递了热量给乙物体,说明甲物体内能大B.物体的内能增加,温度一定升高C.扩散现象是由分子无规则运动产生的D.两物体温度相同,内能一定相同9.科技人员研发了采用氢能源系统的“未来汽车”,此氢能源汽车充氢气3分钟可续航650千米,它采用氢气作为燃料主要是因为氢气具有()A.较小的密度B.较低的沸点C.较高的热值D.较大的比热容10.关于温度、热量和内能,下列说法中正确的是()A.热量可以从内能小的物体传递到内能大的物体B.0 ℃的冰水混合物内能为零C.水的温度越高,所含热量越多D.冰在熔化过程中吸收热量,温度和内能均不变11.下列小实验能达到预期目的的是()①端来一盘美味佳肴,香气扑鼻,说明分子在不停地做无规则运动②将红墨水滴在不同温度的等量水中,通过现象能证明温度升高,分子运动变剧烈③两玻璃使劲挤压后无法合并成一块玻璃,说明分子间有斥力④用手捏海绵,海绵体积变小了,说明分子间有间隙A.①②B.②④C.①④D.②③12.【新题】如图装置,将温度传感器、两个试管固定在铁架台上,两试管装有质量相同的不同种液体,温度传感器的探头部分与试管内的液体良好接触,传感器通过数据采集线与计算机相连接,在计算机上得到的实验图像如图所示,下列说法正确的是()A.加热t1时间,甲吸收热量多B.甲的比热容大C.甲、乙升高相同的温度,甲吸收热量多D.吸收相同的热量,甲升温比乙多二、填空题(19、20题每题2分,其余每空1分,共20分)13.如图所示是一款3D打印笔。
华东师大版九年级科学上册第1早达标检测卷(120分,60分钟)(可能用到的相对原子质量:H: 1 C: 12 0: 16 Mg: 24 S: 32 Cl: 35.5Ca:40 Zn: 65)一、选择题(每小题2分,共20分)1.关于化学方程式CH4 + 202 点燃C02+ 2H2O的描述正确的是()A.甲烷加氧气在点燃条件下,反应生成二氧化碳和水B.1个甲烷和2个氧气在点燃条件下,生成1个二氧化碳和2个水C.1个CH4分子和2个02分子在点燃条件下,生成1个C02分子和2个H20分子D.1 g CH4和2 g 02在点燃条件下,生成1 g C02和2 g H202.下列化学方程式书写正确的是()A. 4P + 502 f 点燃_2P205B. Fe + 02 点燃Fe a04C. C + 02 点燃C02D. Mg + 02 点燃Mg023.摩托罗拉公司研发了一种以甲醇为原料的新型手机电池,其容量为锂电池的10倍,可连续使用一个月才充一次电。
其电池反应原理为:2CH3OH + 3X +4NaOH===2Na2CO3+ 6H2O,其中X 的化学式为()A. O2B. COC. CO2D. H24 .红磷在密闭容器中(含有空气)燃烧,容器内有关的量随时间变化的图像正确的F列对图示反应的理解中,正确的是(F 列对图示反应的理解中,正确的是(IH ■间 5 •以下是某化学反应的微观示意图 分别表示不同元素的原子),柿樹质M豎(“ ”A.该反应属于化合反应B.反应物和生成物中共含有三种元素C.反应中只有一种单质D.参加反应的物质分子个数之比为1:16.建立基本的化学观念可以让我们更好地理解化学,如形成守恒观念,可以更好地理解质量守恒定律。
下列表述正确的是() A •每1个C 原子和1个02分子反应,生成2个CO 2分子B . 32 g S 与32 g 02完全反应,生成64 g SQC •镁条燃烧后固体质量增加,故质量守恒定律不是普遍规律D •根据:蜡烛+氧气 ---- 点燃二氧化碳+水,则蜡烛中一定含有C 、H 、 0三种元素7. 高氯酸是已知酸中酸性最强的酸,一定溶质质量分数的高氯酸加热到 92 °C 以上会发生爆炸,其化学方程式为:4HCIO 4△ 一2Cbf + 702 T+ 2H 2O , 该反应的基本类型属于( )A .化合反应B •分解反应C.复分解反应 D •置换反应 8 •工业用盐亚硝酸钠(NaN02)有毒,其外观与食盐极为相似,在隔绝空气并强热条件下,亚硝酸钠能分解放出一种红棕色气体,该气体可能是 ()KCI0 3和MnO 2固体混合物受热过程中,某变量y 随时 间的变化趋势,纵坐标表示的可能是()oo ■ >9. A . N 2 B . N02 C . 02 D . NH 3F 列有关氧气的制取、 收集、验满、 性质的实验中错误的是() MnO,制取 A10.如图表示一定质量的 收莫B C DA .固体中氧元素的质量B •生成02的质量D .固体中钾元素的质量11.氧气是我们学习过的一种重要物质,以下对氧气的认识有错误的是 ()A .氧气既能燃烧又能支持燃烧B .氧气用于炼钢是利用了它的化学性质C .硫在氧气中燃烧发出明亮的蓝紫色火焰D .氧气和臭氧(03)都是氧元素形成的单质12.在化学反应A + B===C + D 中,若有5 g A 与11 g B 恰好完全反应,生成7 gC 和一定质量的D ,则D 的质量为() A . 5 gB . 16 gC . 9 gD . 23 g 13.如图是通过白磷燃烧来验证质量守恒定律的实验,下列说法错误的是 () A .反应前锥形瓶内白磷和氧气的总质量一定等于反应后生成五氧化二磷的质 气球细沙 B •白磷燃烧结束,锥形瓶应冷却后再放到天平上 称量D .瓶底的细沙起隔热作用14. 一定质量的镁条在氧气中完全燃烧后生成氧化镁,固体质量随时间的变化关 系如图所示。
九上数学第一章测试题姓名:分数:一、选择题(每题3分,共30分)1、下列图形中只是中心对称图形而不是轴对称图形的是()A.平行四边形B.菱形C.正方形D.矩形2、正方形具有而菱形不具有的性质是()A、四个角都是直角B、两组对边分别相等C、内角和为0360D、对角线平分对角3、下列说法中的错误的是()A.一组邻边相等的矩形是正方形B.一组邻边相等的平行四边形是菱形C.一组对边相等且有一个角是直角的四边形是矩形D.一组对边平行且相等的四边形是平行四边形4 、顺次连接一个四边形的各边中点,得到了一个矩形,则下列四边形中满足条件的是()①平行四边形; ②菱形; ③矩形④对角线互相垂直的四边形.A.①③B.②③C.③④D.②④5、已知一矩形的两边长分别为10 cm和15 cm,其中一个内角的平分线分长边为两部分,这两部分的长为()A.6 cm和9 cmB. 5 cm和10 cmC. 4 cm和11 cmD. 7 cm和8 cm6、菱形的周长为20,两邻角的比为2∶1,则一组对边的距离为()A、32B、332C、3 3D、5327、如图,在矩形中,分别为边的中点.若,,则图中阴影部分的面积为()A.3B.4C.6D.88、如图,在菱形中,,∠,则对角线等于()A.20B.15C.10D.59、如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是()A.24°B.33°C.42°D.43°10、如图所示,在矩形ABCD中,AB= 2,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A. 2B. 3C.1D.1.5二、填空题(每题3分,共15分)11、正方形的一条对角线和一边所成的角是度.12、菱形的两条对角线长分别是6和8,则菱形的面积是13、从矩形的一个顶点作一条对角线的垂线,这条垂线分这条对角线成1:3两部分,则矩形的两条对角线夹角为.14、正方形ABCD中,AB=2,点E是线段CD的中点,P为线段BD上的任意一点,则PC+PE 的最小值为_________.15、如图,在边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°,…,按此规律所作的第n个菱形的边长是________.三、解答题(共55分)16、(8分)如图,在四边形ABCD中,AD∥BC,AC的垂直平分线交AD,BC于点E,F.求证:四边形AECF是菱形.17、(10分)如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;(2)若AB=3,BC=4,求四边形OCED的面积.18、(10分)如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE =CF.(1)求证:△BCE≌△DCF;(2)若∠FDC=30°,求∠BEF的度数.19、(12分)如图,在菱形ABCD中,AB=4,∠BAD=120°,以点A为顶点的一个60°的角∠EAF绕点A旋转,∠EAF的两边分别交BC,CD于点E,F,且E,F不与B,C,D重合,连接EF.(1)求证:BE=CF.(2)在∠EAF绕点A旋转的过程中,四边形AECF的面积是否发生变化?如果不变,求出其定值;如果变化,请说明理由.20、(15分)如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN 交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.(1)探究线段OE与OF的数量关系并说明理由.(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?说明理由.(3)当点O在边AC上运动时,四边形BCFE________是菱形(填“可能”或“不可能”).请说明理由.答案解析:1-10 AACDB DBDBD11、45 12、24 13、60°或120° 14、√5 15、(√3)n−116.证明:∵EF 垂直平分AC , ∴∠AOE =∠COF =90°,OA =OC. ∵AD ∥BC ,∴∠OAE =∠OCF. ∴△AOE ≌△COF(ASA ). ∴AE =CF. 又∵AE ∥CF , ∴四边形AECF 是平行四边形. ∵EF ⊥AC , ∴四边形AECF 是菱形.17.(1)证明:∵DE ∥AC ,CE ∥BD ,∴四边形OCED 为平行四边形.∵四边形ABCD 为矩形,∴OD =OC. ∴四边形OCED 为菱形.(2)解:∵四边形ABCD 为矩形, ∴BO =DO =12BD. ∴S △OCD =S △OCB =12S △ABC =12×12×3×4=3. ∴S 菱形OCED =2S △OCD =6. 18.(1)证明:在△BCE 与△DCF 中,⎩⎪⎨⎪⎧BC =DC ,∠BCE =∠DCF ,CE =CF ,∴△BCE ≌△DCF.(2)解:∵△BCE ≌△DCF , ∴∠EBC =∠FDC =30°. ∵∠BCD =90°,∴∠BEC =60°. ∵EC =FC ,∠ECF =90°, ∴∠CEF =45°.∴∠BEF =105°.19.(1)证明:如图,连接AC. ∵四边形ABCD 为菱形,∠BAD =120°, ∴∠ABE =∠ACF =60°, ∠1+∠2=60°. ∵∠3+∠2=∠EAF =60°,∴∠1=∠3. ∵∠ABC =60°,AB =BC , ∴△ABC 为等边三角形.∴AC =AB. ∴△ABE ≌△ACF. ∴BE =CF.(2)解:四边形AECF 的面积不变. 由(1)知△ABE ≌△ACF , 则S △ABE =S △ACF ,故S 四边形AECF =S △AEC +S △ACF =S △AEC +S △ABE =S △ABC .如图,过A 作AM ⊥BC 于点M ,则BM =MC =2,∴AM =AB 2-BM 2=42-22=2 3.∴S△ABC=12BC·AM=12×4×23=4 3. 故S四边形AECF=4 3.(第23题)20.解:(1)OE=OF.理由如下:∵CE是∠ACB的平分线,∴∠ACE=∠BCE.又∵MN∥BC,∴∠NEC=∠BCE. ∴∠NEC=∠ACE. ∴OE=OC.∵CF是∠ACD的平分线,∴∠OCF=∠FCD. 又∵MN∥BC,∴∠OFC=∠FCD. ∴∠OFC=∠OCF. ∴OF=OC. ∴OE=OF.(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角时,四边形AECF是正方形.理由如下:∵当点O运动到AC的中点时,AO=CO,又∵EO=FO,∴四边形AECF是平行四边形.∵FO=CO,∴AO=CO=EO=FO.∴AO+CO=EO+FO,即AC=EF. ∴四边形AECF是矩形.已知MN∥BC,当∠ACB=90°时,∠AOE=90°,∴AC⊥EF. ∴四边形AECF是正方形.(3)不可能理由如下:连接BF,∵CE平分∠ACB,CF平分∠ACD,∴∠ECF=12∠ACB+12∠ACD=12(∠ACB+∠ACD)=90°.若四边形BCFE是菱形,则BF⊥EC.但在一个三角形中,不可能存在两个角为90°,故四边形BCFE不可能为菱形.。
北师大版九年级数学上册第一章达标测试卷一、选择题(每题3分,共30分)1.如图,已知菱形ABCD 的边长等于2,∠DAB =60°,则对角线BD 的长为( )A .1B. 3C .2D .2 3(第1题) (第3题) (第4题) (第6题) 2.已知正方形的面积为36,则其对角线的长为( )A .6B .6 2C .9D .9 23.如图,矩形ABCD 的对角线AC =8 cm ,∠AOD =120°,则AB 的长为( )A. 3 cmB .2 cmC .2 3 cmD .4 cm4.如图,菱形ABCD 的对角线AC ,BD 的长分别为6 cm ,8 cm ,则这个菱形的周长为( )A .5 cmB .10 cmC .14 cmD .20 cm5.下列命题中,真命题是( )A .对角线相等的四边形是矩形B .对角线互相垂直的四边形是菱形C .对角线互相平分的四边形是平行四边形D .对角线互相垂直平分的四边形是正方形6.如图,EF 过矩形ABCD 对角线的交点O ,分别交AB ,CD 于点E ,F ,那么阴影部分的面积是矩形ABCD 的面积的( ) A.15B.14C.13D.3107.如图,在△ABC 中,AB =AC ,四边形ADEF 为菱形,S △ABC =83,则S 菱形ADEF 等于( )A .4B .4 6C .4 3D .28(第7题) (第9题) (第10题)8.在四边形ABCD中,点O是对角线的交点,能判定这个四边形是正方形的条件是() A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠BAD=∠BCDC.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC9.如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于点E,若线段AE=6,则四边形ABCD的面积是()A.3 B.4 C.2 6 D.610.如图,把矩形OABC放入平面直角坐标系中,点B的坐标为(10,8),点D是OC上一点,将△BCD沿BD折叠,点C恰好落在OA上的点E处,则点D的坐标是() A.(0,4) B.(0,5) C.(0,3) D.(0,2)二、填空题(每题3分,共30分)11.在Rt△ABC中,如果斜边上的中线CD=4 cm,那么斜边AB=________.12.已知菱形的两条对角线长分别为2 cm,3 cm,则它的面积是________.13.如图,一活动菱形衣架中,菱形的边长均为16 cm,若墙上钉子间的距离AB=BC=16 cm,则∠1=________.(第13题)(第16题)(第17题)14.已知矩形ABCD的对角线AC,BD相交于点O,当添加条件__________时,矩形ABCD 是正方形(只填一个即可).15.矩形的对角线相交所成的角中,有一个角是60°,这个角所对的边长为1 cm,则其对角线长为________,矩形的面积为________.16.如图,菱形ABCD的顶点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为________.17.如图,在正方形ABCD的外侧作等边三角形ADE,则∠BED=________.18.如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为________.(第18题)(第19题)(第20题)19.如图,已知正方形ABCD的边长为1,连接AC,BD,CE平分∠ACD交BD于点E,则DE=________.20.如图,在正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G.下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE.其中正确结论的序号为__________.三、解答题(21题8分,26题12分,其余每题10分,共60分)21.如图,在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:BE=CF.22.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.(1)求证:BD=EC;(2)若∠E=50°,求∠BAO的大小.23.如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB,EA,延长BE交AD于点F.(1)求证:△ADE≌△BCE;(2)求∠AFB的度数.24.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.(1)在AC上找一点P,使△BPE的周长最小(作图说明);(2)求出△BPE周长的最小值.25.如图,在等腰三角形ABC中,AB=AC,AH⊥BC于点H,点E是AH上一点,延长AH 至点F,使FH=EH,连接BE,CE,BF,CF.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.26.在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG,CG,如图①,易证EG=CG且EG⊥CG.(1)将△BEF绕点B逆时针旋转90°,如图②,则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.(2)将△BEF绕点B逆时针旋转180°,如图③,则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.答案一、1.C 2.B 3.D 4.D 5.C 6.B7.C8.C9.D10.C二、11.8 cm12.3 cm213.120°14.AC⊥BD(答案不唯一)15.2 cm; 3 cm216.(4,4)17.45°18.501319.2-120.①②③⑤三、21.证明:∵四边形ABCD为矩形,∴OA=OC,OB=OD,AC=BD.∴BO=CO.∵BE⊥AC于点E,CF⊥BD于点F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF(AAS).∴BE=CF.22.(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AB=CD.又∵E在AB的延长线上,且BE=AB,∴BE∥CD,BE=CD.∴四边形BECD是平行四边形.∴BD=EC.(2)解:∵四边形BECD是平行四边形,∴BD∥CE.∴∠ABO=∠E=50°.又∵四边形ABCD是菱形,∴AC⊥BD.∴∠BAO=90°-∠ABO=40°.23.(1)证明:∵四边形ABCD是正方形,∴∠DAB=∠ADC=∠BCD=90°,AD=BC.∵△CDE 是等边三角形,∴∠CDE =∠DCE =60°,DE =CE . ∴∠ADE =∠BCE =30°. 在△ADE 和△BCE 中,⎩⎨⎧AD =BC ,∠ADE =∠BCE ,DE =CE ,∴△ADE ≌△BCE (SAS). (2)解:∵△ADE ≌△BCE , ∴AE =BE . ∴∠BAE =∠ABE .又∵∠BAE +∠DAE =90°, ∠ABE +∠AFB =90°, ∴∠DAE =∠AFB .∵∠ADE =30°,DE =DC =DA , ∴∠DAE =75°. ∴∠AFB =75°.24.解:(1)如图,连接DE ,交AC 于点P ′,连接BP ′,则此时P ′B +P ′E 的值最小,即当点P 在点P ′处时,△BPE 的周长最小.(2)∵四边形ABCD 是正方形, ∴B ,D 关于AC 对称. ∴P ′B =P ′D . ∴P ′B +P ′E =DE . ∵BE =2,AE =3BE , ∴AE =6.∴AD =AB =8. ∴DE =62+82=10. ∴PB +PE 的最小值是10.∴△BPE的周长的最小值为10+BE=10+2=12. 25.证明:(1)∵AB=AC,AH⊥BC,∴BH=CH.又∵FH=EH,∴四边形EBFC是平行四边形.又∵EF⊥BC,∴四边形EBFC是菱形.(2)如图所示.∵四边形EBFC是菱形,∴∠2=∠3=12∠ECF.∵AB=AC,AH⊥BC,∴∠4=12∠BAC.又∵∠BAC=∠ECF,∴∠4=∠3.∵∠4+∠1+∠2=90°,∴∠3+∠1+∠2=90°,即AC⊥CF.26.解:(1)EG=CG,EG⊥CG.(2)EG=CG,EG⊥CG.证明如下:延长FE交DC的延长线于点M,连接MG,如图所示.易得∠AEM=90°,∠EBC=90°,∠BCM=90°,∴四边形BEMC 是矩形.∴BE =CM ,BC =EM ,∠EMC =90°. 易知∠ABD =45°, ∴∠EBF =45°. 又∵∠BEF =90°,∴△BEF 为等腰直角三角形. ∴BE =EF ,∠F =45°. ∴EF =CM .∵∠EMC =90°,FG =DG , ∴MG =12FD =FG . ∵BC =EM ,BC =CD , ∴EM =CD . ∵EF =CM , ∴FM =DM . 又∵FG =DG ,∴∠CMG =12∠EMC =45°. ∴∠F =∠CMG . 在△GFE 和△GMC 中,⎩⎨⎧FG =MG ,∠F =∠GMC ,EF =CM ,∴△GFE ≌△GMC (SAS). ∴EG =CG ,∠FGE =∠MGC . ∵MF =MD ,FG =DG , ∴MG ⊥FD .∴∠FGE +∠EGM =90°. ∴∠MGC +∠EGM =90°, 即∠EGC =90°. ∴EG ⊥CG .九年级数学上册期末达标检测卷一、选择题(每题4分,共40分)1.已知a,d,c,b是成比例线段,其中a=3 cm,b=2 cm,c=6 cm,则d的长度为()A.4 cm B.1 cm C.9 cm D.5 cm2.在反比例函数y=k-1x图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是()A.k<0 B.k>0 C.k<1 D.k>13.对于抛物线y=-12(x+2)2+3,有下列结论:①抛物线的开口向下;②对称轴为直线x=2;③顶点坐标为(-2,3);④当x>2时,y随x的增大而减小.其中正确结论的个数为()A.1 B.2 C.3 D.44.如图,在▱ABCD中,E是AD边的中点,连接BE并延长交CD的延长线于点F,则△EDF与△BCF的周长之比是()A.1:2 B.1:3 C.1:4 D.1:55.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=5,BC =2,则sin∠ACD的值为()A.52 B.2 55 C.53 D.236.如图,P为线段AB上一点,AD与BC相交于点E,∠CPD=∠A=∠B,BC 交PD于点F,AD交PC于点G,则图中相似三角形有()A.1对B.2对C.3对D.4对7.如图,在直角平面坐标系中,△OAB 的顶点为O (0,0),A (4,3),B (3,0).以点O 为位似中心,在第三象限内作与△OAB 的相似比为13的位似图形△OCD ,则点C 的坐标为( )A .(-1,-1) B.⎝ ⎛⎭⎪⎫-43,-1 C.⎝ ⎛⎭⎪⎫-1,-43 D .(-2,-1) 8.如图,在笔直的海岸线l 上有A ,B 两个观测站,且AB =2 km.从A 站测得船C 在北偏东45°方向,从B 站测得船C 在北偏东22.5°方向,且tan 22.5°=2-1,则船C 离海岸线l 的距离(即CD 的长)为( ) A .4 kmB .(2+2)kmC .2 2 kmD .(4-2)km9.如图,已知边长为4的正方形EFCD 截去一角成为五边形ABCDE ,其中AF=2,BF =1.在AB 上找一点P ,使得矩形PNDM 有最大面积,则矩形PNDM 面积的最大值为( ) A .8B .12C.252D .1410.如图,在平面直角坐标系中,抛物线y =-x 2+2 3x 的顶点为A ,且与x轴的正半轴交于点B ,点P 为该抛物线对称轴上一点,则OP +12AP 的最小值为( ) A.3+2214B.3+232C .3D .2 3二、填空题(每题5分,共20分)11.如图,在由边长相同的小正方形组成的网格中,点A ,B ,C ,D 都在这些小正方形的顶点上,AB ,CD 相交于点P ,则tan ∠APD 的值是________.12.如图,点P 是反比例函数y =43x (x >0)图象上一动点,在y 轴上取点Q ,使得以P ,Q ,O 为顶点的三角形是含有30°角的直角三角形,则符合条件的点Q 的坐标是________________.13.如图是二次函数y =ax 2+bx +c (a ≠0)的图象,其与x 轴的交点的横坐标分别为x 1,x 2,其中-2<x 1<-1,0<x 2<1,下列结论:①abc >0;②4a -2b +c <0;③2a -b <0.其中正确的有____________(填序号).14.如图,在矩形纸片ABCD 中,AB =6,BC =10,点E 在CD 上,将△BCE 沿BE 折叠,使点C 恰好落在边AD 上的点F 处;点G 在AF 上,将△ABG 沿BG 折叠,使点A 恰好落在线段BF 上的点H 处,有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③S △ABG =32S △FGH ;④AG +DF =FG .其中正确的有____________(填序号).三、解答题(15~18题每题8分;19,20题每题10分;21,22题每题12分;23题14分,共90分)15.计算:(-1)2 022-6tan30°+⎝ ⎛⎭⎪⎫12-2+|1-3|.16.已知抛物线y =12x 2-4x +7与直线y =12x 交于A ,B 两点(点A 在点B 左侧).(1)求A ,B 两点的坐标;(2)求抛物线顶点C 的坐标,并求△ABC 的面积.17.如图,在△ABC中,AB=43,AC=10,∠B=60°,求△ABC的面积.18.如图,△ABC三个顶点的坐标分别为A(1,2),B(3,1),C(2,3),以原点O 为位似中心,将△ABC放大为原来的2倍得到△A′B′C′.(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法);(2)计算△A′B′C′的面积.19.如图,已知在正方形ABCD中,BE平分∠DBC,交CD边于点E,将△BCE 绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.(1)求证:△BDG∽△DEG;(2)若EG·BG=4,求BE的长.20.设P(x,0)是x轴上的一个动点,它与原点的距离为y1.(1)求y1关于x的函数表达式,并画出这个函数的图象;(2)若反比例函数y2=kx的图象与函数y1的图象相交于点A,且点A的纵坐标为2.①求k的值;②结合图象,当y1>y2时,写出x的取值范围.21.如图,某大楼DE的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:3,AB=8米,AE=12米.(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:2≈1.414,3≈1.732)22.某公司经销一种绿茶,每千克成本为50元.经市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体表达式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y元,解答下列问题:(1)求y与x的函数表达式;(2)当x取何值时,y的值最大?(3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2 250元的销售利润,销售单价应定为多少?23.矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得点B落在CD边上的点P处.(1)如图①,已知折痕与边BC交于点O.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长;(2)如图②,在(1)的条件下,擦去AO和OP,连接BP.动点M在线段AP上(不与点P,A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问动点M,N在移动的过程中,线段EF的长度是否发生变化?若不变,求出线段EF的长度;若变化,说明理由.答案一、1.B 2.D3.C【点拨】∵a<0,∴抛物线的开口向下,①正确;抛物线y=-12(x+2)2+3的对称轴为直线x=-2,②错误;顶点坐标为(-2,3),③正确;④抛物线开口向下,当x>2时,图象是下降趋势,y随x的增大而减小,④正确.故选C.4.A【点拨】在▱ABCD中,AD=BC,AD∥BC,∵E是AD的中点,∴DE=12AD=12BC.由AD∥BC可得,△EDF∽△BCF.它们的周长比等于相似比,∴周长比等于ED BC=12BC:BC=1:2.故选A.5.C【点拨】∵在Rt△ABC中,∠ACB=90°,AC=5,BC=2,∴AB =AC 2+BC 2=(5)2+22=3. ∵∠ACB =90°,CD ⊥AB , ∴∠ACD +∠BCD =90°,∠B +∠BCD =90°,∴∠ACD =∠B , ∴sin ∠ACD =sin B =AC AB =53. 故选C.6.C 【点拨】∵∠CPD =∠A ,∠D =∠D ,∴△ADP ∽△PDG ,∴∠APD =∠PGD ,∴∠FPB =∠AGP .∵∠CPF =∠B ,∠C =∠C ,∴△CPF ∽△CBP ,∴∠CFP =∠CPB ,∴∠PFB =∠APG ;在△AGP 和△BPF 中,∠AGP =∠BPF ,∠APG =∠BFP ,∴△AGP ∽△BPF .故选C. 7.B 8.B9.B 【点拨】延长NP 交EF 于点G ,设PG =x ,则PN =4-x . ∵PG ∥BF ,∴△APG ∽△ABF , ∴AG AF =PG BF ,即AG 2=x 1, 解得AG =2x ,∴PM =EG =EA +AG =2+2x ,∴S 矩形PNDM =PM ·PN =(2+2x )(4-x )=-2x 2+6x +8=-2⎝ ⎛⎭⎪⎫x -322+252(0≤x ≤1),当x =1时,矩形PNDM 的面积最大,最大值为12.故选B .10.C 【点拨】连接AB ,过点P 作PC ⊥AB 于点C .设抛物线的对称轴与x 轴的交点为点D .易求出抛物线的对称轴为直线x =3,顶点A (3,3),故BD =OD =3,AD =3,在Rt △ABD 中,tan ∠BAD =BD AD =33,∴∠BAD =30°,∴PC =12AP .当O ,P ,C 三点共线时,OP +PC 的长最短,最短距离为sin ∠OBC ·OB =sin 60°×2 3=3.∴OP +12AP 的最小值为3.故选C.二、11.212.(0,23)或(0,2)或⎝ ⎛⎭⎪⎫0,833或(0,8) 13.①②③ 【点拨】①∵图象开口向下, ∴a <0,∵图象的对称轴在y 轴左侧, ∴-b2a <0,而a <0,∴b <0, ∵图象与y 轴的交点在正半轴上, ∴c >0,∴abc >0,故结论正确. ②∵-2<x 1<-1,∴当x =-2时,y =4a -2b +c <0,故结论正确. ③∵-2<x 1<-1,0<x 2<1, ∴-b2a >-1,∵a <0, ∴2a -b <0,故结论正确. 故正确的结论有①②③.14.①③④ 【点拨】∵△BCE 沿BE 折叠,点C 恰好落在边AD 上的点F 处, ∴∠1=∠2,CE =FE ,BF =BC =10.在Rt △ABF 中,∵AB =6,BF =10, ∴AF =102-62=8,∴DF =AD -AF =10-8=2.设EF =x ,则CE =x ,DE =CD -CE =6-x .在Rt △DEF 中,∵DE 2+DF 2=EF 2,∴(6-x )2+22=x 2,解得x =103,∴DE =83.∵△ABG 沿BG 折叠,点A 恰好落在线段BF 上的点H 处,∴∠3=∠4,BH =BA =6,AG =HG ,∴∠EBG =∠2+∠3=12∠ABC =45°,∴①正确.HF =BF -BH =10-6=4,设AG =y ,则GH =y ,GF =8-y .在Rt △HGF 中,∵GH 2+HF 2=GF 2,∴y 2+42=(8-y )2,解得y =3,∴AG =GH =3,GF =5.∵∠A =∠D ,AB DE =94,AG DF =32,∴AB DE ≠AGDF ,∴△ABG 与△DEF 不相似,∴②错误.∵S △ABG =12AB ·AG =12×6×3=9,S △FGH =12GH ·HF =12×3×4=6,∴S △ABG =32S △FGH ,∴③正确.∵AG +DF =3+2=5,而FG =5,∴AG +DF =FG ,∴④正确.三、15.解:原式=1-6×33+4+3-1=4- 3.16.解:(1)联立⎩⎪⎨⎪⎧y =12x 2-4x +7,y =12x ,解得⎩⎨⎧x =2,y =1或⎩⎪⎨⎪⎧x =7,y =72.∴A (2,1),B ⎝ ⎛⎭⎪⎫7,72.(2)∵y =12x 2-4x +7=12(x -4)2-1, ∴顶点C 的坐标为(4,-1).过顶点C 作CD ∥x 轴交直线y =12x 于点D ,如图.在y =12x 中,令y =-1,得12x =-1,解得x =-2,∴CD =6,∴S △ABC =S △BCD -S △ACD =12×6×⎝ ⎛⎭⎪⎫72+1-12×6×(1+1)=7.5.17.解:过点A 作AD ⊥BC 于点D .在Rt △ABD 中,AD =AB ·sin B =4 3×32=6,BD =AB ·cos B =4 3×12=2 3.在Rt △ACD 中,CD =AC 2-AD 2=102-62=8, ∴BC =BD +CD =2 3+8.∴S △ABC =12BC ·AD =12×(23+8)×6=63+24. 18.解:(1)如图.(2)S △A ′B ′C ′=4×4-12×2×2-12×2×4-12×2×4=6.19.(1)证明:∵BE 平分∠DBC , ∴∠DBG =∠CBE ,根据旋转的性质,得∠EDG =∠CBE , ∴∠DBG =∠EDG , 又∵∠DGB =∠EGD , ∴△BDG ∽△DEG .(2)解:由(1)知△BDG ∽△DEG , ∴BG DG =DGEG ,∴DG 2=EG ·BG . ∵EG ·BG =4,∴DG 2=4, ∴DG =2(负值舍去).∵∠EDG =∠CBE ,∠DEG =∠BEC , ∴∠BGD =∠BCE =90°. ∴∠BGF =∠BGD =90°.又∵BG =BG ,∠DBG =∠FBG , ∴△DBG ≌△FBG .∴DG =FG ,∴DF =2DG =4, 由题意可知,BE =DF , ∴BE =4.20.解:(1)由题意得,y 1=||x ,即y 1=||x =⎩⎨⎧x ,x ≥0,-x ,x <0.函数图象如图所示.(2)①∵点A的纵坐标为2,点A在函数y1的图象上,∴||x=2,即x=±2.∴点A 的坐标为(2,2)或(-2,2).∴k=±4.②当k=4时,图象如图①,当y1>y2时,x的取值范围为x<0或x>2;当k=-4时,图象如图②,当y1>y2时,x的取值范围为x<-2或x>0. 21.解:(1)过点B作BG⊥DE于点G,如图.在Rt△ABH中,tan ∠BAH=13=33,∴∠BAH=30°,∴BH=12AB=4(米).∴点B距水平面AE的高度BH为4米.(2)由(1)知BH=4(米),∴GE=BH=4(米),AH=4 3(米).∴BG=HE=AH+AE=(4 3+12)米.在Rt△BGC中,∠CBG=45°,∴CG=BG=(4 3+12)米.在Rt△ADE中,∠DAE=60°,AE=12米,∴DE=AE·tan ∠DAE=12·tan 60°=12 3(米).∴CD=CG+GE-DE=4 3+12+4-12 3=16-8 3≈16-8×1.732≈2.1(米).∴广告牌CD的高度约为2.1米.22.解:(1)由题意得y=(x-50)·w=(x-50)·(-2x+240)=-2x2+340x-12 000,∴y与x的函数表达式为y=-2x2+340x-12 000.(2)y=-2x2+340x-12 000=-2(x-85)2+2 450,∴当x=85时,y的值最大.(3)当y=2 250时,可得-2(x-85)2+2 450=2 250,解这个方程,得x1=75,x2=95,根据题意知,x=95不合题意,故舍去,∴销售单价应定为75元/千克.23.(1)①证明:如图,∵四边形ABCD 是矩形,∴∠C =∠D =∠B =90°,∴∠1+∠3=90°.由折叠可得∠APO =∠B =90°,∴∠1+∠2=90°.∴∠3=∠2.又∵∠C =∠D ,∴△OCP ∽△PDA .②解:∵△OCP 与△PDA 的面积比为1:4,且△OCP ∽△PDA , ∴OP P A =CP DA =12.∴CP =12AD =4,AP =2OP .设OP =x ,则易得CO =8-x .在Rt △PCO 中,∠C =90°,由勾股定理得 x 2=(8-x )2+42.解得x =5.∴AB =AP =2OP =10.(2)解:线段EF 的长度不变.作MQ ∥AN ,交PB 于点Q ,如图.∵AP =AB ,MQ ∥AN ,∴∠APB=∠ABP=∠MQP.∴MP=MQ.又∵BN=PM,∴BN=QM.∵MQ∥AN,∴∠QMF=∠BNF,∠MQF=∠FBN,∴△MFQ≌△NFB.∴QF=FB.∴QF=12QB.∵MP=MQ,ME⊥PQ,∴EQ=12PQ.∴EF=EQ+QF=12PQ+12QB=12PB.∵PC=4,BC=8,∠C=90°. ∴PB=82+42=4 5,∴EF=12PB=2 5.∴动点M,N在移动的过程中,线段EF的长度不变,恒为2 5.。
第一章达标测试卷一、选择题(每题4分,共40分)1.下列说法中,错误的是()A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形2.如图,矩形ABCD的对角线AC=8 cm,∠AOD=120°,则AB的长为()A. 3 cm B.2 cm C.2 3 cm D.4 cm(第2题)3.下列给出的条件中,不能判断一个四边形是矩形的是()A.一组对边平行且相等,有一个内角是直角B.有三个角是直角C.两条对角线把四边形分成两对全等的等腰三角形D.一组对边平行,另一组对边相等,且两条对角线相等4.如图,在边长为1的正方形网格中,格点四边形ABCD是菱形,则此四边形的周长等于()A.6 B.12 C.413 D.24(第4题)5.如图,EF过矩形ABCD对角线的交点O,分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD的面积的()A.15 B.14 C.13 D.3106.如图,在△ABC中,AB=AC,四边形ADEF为菱形,S△ABC=83,则S菱形ADEF等于()A.4 B.4 6 C.4 3 D.28(第6题)7.在四边形ABCD中,点O是对角线的交点,能判定这个四边形是正方形的条件是()A.AC=BD,AB∥CD,AB=CDB.AD∥BC,∠BAD=∠BCDC.AO=BO=CO=DO,AC⊥BDD.AO=CO,BO=DO,AB=BC8.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形9.在矩形纸片ABCD中,AD=4 cm,AB=10 cm,按如图所示的方式折叠,使点B与点D重合,折痕为EF,则DE长为()A.4.8 cm B.5 cm C.5.8 cm D.6 cm(第9题)10.如图,在正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC 交EF于点G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE.其中正确的个数为()A.2 B.3 C.4 D.5(第10题)二、填空题(每题4分,共32分)11.在Rt△ABC中,如果斜边上的中线CD=4 cm,那么斜边AB=________.12.已知菱形的两条对角线长分别为2 cm,3 cm,则它的周长是________.13.如图,一活动菱形衣架中,菱形的边长均为16 cm,若墙上钉子间的距离AB=BC=16 cm,则∠1=________.(第13题)14.矩形的对角线相交所成的角中,有一个角是60°,这个角所对的边长为1 cm,则其对角线长为________,矩形的面积为________.15.如图,菱形ABCD的顶点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C 的坐标为________.(第15题)16.如图,在正方形ABCD的外侧作等边三角形ADE,则∠BED=________.(第16题)17.如图,用两张对边平行的纸条交叉重叠放在一起,则四边形ABCD为________形;两张纸条互相垂直时,四边形ABCD为________形;若两张纸条的宽度相同,则四边形ABCD为________形.(第17题)18.如图,已知正方形ABCD的边长为1,连接AC,BD,CE平分∠ACD交BD于点E,则DE=________.(第18题)三、解答题19.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长和是86 cm,对角线长是13 cm,那么矩形ABCD的周长是多少?20.如图,在矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为点E,F.求证:BE=CF.21.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.(1)求证:BD=EC;(2)若∠E=50°,求∠BAO的大小.22.如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB,EA,延长BE交边AD于点F.(1)求证:△ADE≌△BCE;(2)求∠AFB的度数.23.如图,在等腰三角形ABC中,AB=AC,AH⊥BC于点H,点E是AH上一点,延长AH 至点F,使FH=EH,连接BE,CE,BF,CF.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.24.如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索:过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP 是菱形,请在下面的框中补全他的证明思路.由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证▱MNQP是菱形,只要证NM=NQ.由已知条件________,MN∥EF,可证NG=NF,故只要证GM=FQ,即证△MGE≌△QFH.易证________,________,故只要证∠MGE=∠QFH.易证∠MGE=∠GEF,∠QFH=∠EFH,________,即可得证.(第24题) 25.在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG,CG,如图①,易证EG=CG且EG⊥CG.(1)将△BEF绕点B逆时针旋转90°,如图②,则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想;(2)将△BEF绕点B逆时针旋转180°,如图③,则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.(第25题)答案一、1.D 2.D 3.D 4.C 5.B 6.C7.C8.D9.C点拨:设DE=x cm,则BE=DE=x cm,AE=AB-BE=(10-x)cm,在R t△ADE中,DE2=AE2+AD2,即x2=(10-x)2+16.解得x=5.8.故选C.10.C二、11.8 cm12.213 cm13.120°14.2 cm; 3 cm215.(4,4)16.45°17.平行四边;矩;菱18.2-1三、19.解:∵△AOB,△BOC,△COD,△AOD的周长和为86 cm,且AC=BD=13 cm,∴AB+BC+CD+DA=86-2(AC+BD)=86-4×13=34(cm),即矩形ABCD的周长是34cm.20.证明:∵四边形ABCD为矩形,∴OA=OC,OB=OD,AC=BD.∴BO=CO.∵BE⊥AC于E,CF⊥BD于F,∴∠BEO=∠CFO=90°.又∵∠BOE=∠COF,∴△BOE≌△COF.∴BE=CF.21.(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AB=CD.又∵E在AB的延长线上,且BE=AB,∴BE∥CD,BE=CD.∴四边形BECD是平行四边形.∴BD=EC.(2)解:∵四边形BECD是平行四边形,∴BD∥CE.∴∠ABO=∠E=50°.又∵四边形ABCD是菱形,∴AC⊥BD.∴∠BAO=90°-∠ABO=40°.22.(1)证明:∵四边形ABCD是正方形,∴∠ADC=∠BCD=90°,AD=BC.∵△CDE是等边三角形,∴∠CDE=∠DCE=60°,DE=CE.∵∠ADC=∠BCD=90°,∠CDE=∠DCE=60°,∴∠ADE=∠BCE=30°.在△ADE和△BCE中,∵AD=BC,∠ADE=∠BCE,DE=CE,∴△ADE≌△BCE. (2)解:∵△ADE≌△BCE,∴AE=BE.∴∠BAE=∠ABE.∵∠BAE+∠DAE=90°,∠ABE+∠AFB=90°,∠BAE=∠ABE,∴∠DAE=∠AFB.∵∠ADE=30°,∴∠DAE=75°.∴∠AFB=75°.23.证明:(1)∵AB=AC,AH⊥BC,∴BH=CH.∵FH=EH,∴四边形EBFC是平行四边形.又∵EF⊥BC,∴四边形EBFC是菱形.(2)如图,∵四边形EBFC是菱形,∴∠2=∠3=12∠ECF.∵AB=AC,AH⊥BC,∴∠4=12∠BAC .∵∠BAC =∠ECF ,∴∠4=∠3. ∵∠4+∠1+∠2=90°,∴∠3+∠1+∠2=90°,即AC ⊥CF.(第23题)24.(1)证明:∵EH 平分∠BEF ,∴∠FEH =12∠BEF .∵FH 平分∠DFE ,∴∠EFH =12∠DFE .∵AB ∥CD ,∴∠BEF +∠DFE =180°.∴∠FEH +∠EFH =12(∠BEF +∠DFE )=12×180°=90°.∴∠EHF =180°-(∠FEH +∠EFH )=180°-90°=90°. 同理可证∠EGF =90°. ∵EG 平分∠AEF , ∴∠GEF =12∠AEF .∵∠FEH =12∠BEF ,∠AEF +∠BEF =180°,∴∠GEF +∠FEH =12(∠AEF +∠BEF )=12×180°=90°,即∠GEH =90°.∴四边形EGFH 是矩形.(2)FG 平分∠CFE ;GE =FH ;∠GME =∠FQH ;∠GEF =∠EFH 25.解:(1)EG =CG ,EG ⊥CG . (2)EG =CG ,EG ⊥CG .证明如下:延长FE 交DC 的延长线于点M ,连接MG ,如图所示.(第25题)∵∠AEM =90°,∠EBC =90°, ∠BCM =90°,∴四边形BEMC 是矩形.∴BE =CM ,BC =EM ,∠EMC =90°. 易知,∠ABD =45°,∴∠EBF =45°. 又∵∠BEF =90°,∴△BEF 为等腰直角三角形. ∴BE =EF ,∠F =45°. ∴EF =CM .∵∠EMC =90°,FG =DG , ∴MG =12FD =FG .∵BC =EM ,BC =CD , ∴EM =CD .∵EF =CM ,∴FM =DM . 又∵FG =DG ,∴∠CMG =12∠EMC =45°,∴∠F =∠CMG . 在△GFE 和△GMC 中,FG =MG ∠F =∠GMC , EF =CM ,∴△GFE ≌△GMC .∴EG =CG ,∠FGE =∠MGC .∵MF=MD,FG=DG,∴MG⊥FD,∴∠FGE+∠EGM=90°,∴∠MGC+∠EGM=90°,即∠EGC=90°.∴EG⊥CG.。