数学《算法案例秦九韶算法》教案(新人教A版必修)
- 格式:doc
- 大小:94.50 KB
- 文档页数:6




秦九韶算法 一、三维目标(a )知识与技能了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
(b )过程与方法 模仿秦九韶计算方法,体会古人计算构思的巧妙。
(c )情态与价值观通过对秦九韶算法的学习,了解中国古代数学家对数学的贡献,充分认识到我国文化历史的悠久。
充分认识信息技术对数学的促进。
二、教学重难点重点:1.秦九韶算法的特点难点:1.秦九韶算法的先进性理解三、教学设计 (一)创设情景,揭示课题1.辗转相除法和更相减损术,是求两个正整数的最大公约数的优秀算法,我们将算法转化为程序后,就可以由计算机来执行运算,实现了古代数学与现代信息技术的完美结合.2.对于求n 次多项式的值,在我国古代数学中有一个优秀算法,即秦九韶算法,我们将对这个算法作些了解和探究.(二)研探新知思考1 ).5(,12345)(2345f x x x x x x f 求已知+++++= 21325算法1:需要(5+4+3+2)=14次乘法,5次加法算法2:需要5次乘法,5次加法 秦九韶算法思考2 ).3(,1234567)(234567f x x x x x x x x f 求已知+++++++= 18556 思考3:利用后一种算法求多项式f(x)=a n x n +a n-1x n-1+…+a 1x+a 0的值,这个多项式应写成哪种形式?f(x)=a n x n +a n-1x n-1+…+a 1x+a 0=(a n x n-1+a n-1x n-2+…+a 2x+a 1)x+a 0=((a n x n-2+a n-1x n-3+…+a 2)x+a 1)x+a 0=…=(…((a n x+a n-1)x+a n-2)x+…+a 1)x+a 0.思考4:对于f(x)=(…((a n x+a n-1)x+a n-2)x+…+a 1)x+a 0,由内向外逐层计算一次多项式的值,其算法步骤如何?第一步,计算v 1=a n x+a n-1.第二步,计算v 2=v 1x+a n-2.第三步,计算v 3=v 2x+a n-3.…第n 步,计算v n =v n-1x+a 0.思考5:上述求多项式f(x)=a n x n +a n-1x n-1+…+a 1x+a 0的值的方法称为秦九韶算法,利用该算法求f(x 0)的值,一共需要多少次乘法运算,多少次加法运算?思考6:在秦九韶算法中,记v 0=a n ,那么第k 步的算式是什么?v k =v k-1x+a n-k (k=1,2,…,n)例1 阅读下列程序,说明它解决的实际问题是什么?求多项式43254321)(x x x x x f ++++=,在x=a 时的值.评价一个算法好坏的一个重要标志是运算的次数,如果一个算法从理论上需要超出计算机允许范围内的运算次数,那么这样的算法就只能是一个理论算法.在多项式求值的各种算法中,秦九韶算法是一个优秀算法.作业:《习案》作业九 INPUT “x=”;a n=0y=0WHILE n <5y=y+(n+1)*a ∧n n=n+1WEND PRINT y END。


2019-2020年高中数学 第一章算法初步1.3算法案例第三、四课时 秦九韶算法与排序教案 新人教A 版必修3(1)教学目标(a )知识与技能1.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
2.掌握数据排序的原理能使用直接排序法与冒泡排序法给一组数据排序,进而能设计冒泡排序法的程序框图及程序,理解数学算法与计算机算法的区别,理解计算机对数学的辅助作用。
(b )过程与方法模仿秦九韶计算方法,体会古人计算构思的巧妙。
能根据排序法中的直接插入排序法与冒泡排序法的步骤,了解数学计算转换为计算机计算的途径,从而探究计算机算法与数学算法的区别,体会计算机对数学学习的辅助作用。
(c )情态与价值通过对秦九韶算法的学习,了解中国古代数学家对数学的贡献,充分认识到我国文化历史的悠久。
通过对排序法的学习,领会数学计算与计算机计算的区别,充分认识信息技术对数学的促进。
(2)教学重难点重点:1.秦九韶算法的特点2.两种排序法的排序步骤及计算机程序设计难点:1.秦九韶算法的先进性理解2.排序法的计算机程序设计(3)学法与教学用具学法:1.探究秦九韶算法对比一般计算方法中计算次数的改变,体会科学的计算。
2.模仿排序法中数字排序的步骤,理解计算机计算的一般步骤,领会数学计算在计算机上实施的要求。
教学用具:电脑,计算器,图形计算器(4)教学设想(一)创设情景,揭示课题我们已经学过了多项式的计算,下面我们计算一下多项式1)(2345+++++=x x x x x x f 当时的值,并统计所做的计算的种类及计算次数。
根据我们的计算统计可以得出我们共需要10次乘法运算,5次加法运算。
我们把多项式变形为:1)))1(1(1()(2+++++=x x x x x x f 再统计一下计算当时的值时需要的计算次数,可以得出仅需4次乘法和5次加法运算即可得出结果。
显然少了6次乘法运算。
这种算法就叫秦九韶算法。

1.3算法案例第三、四课时 秦九韶算法与排序(1)教学目标(a )知识与技能1.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
2.掌握数据排序的原理能使用直接排序法与冒泡排序法给一组数据排序,进而能设计冒泡排序法的程序框图及程序,理解数学算法与计算机算法的区别,理解计算机对数学的辅助作用。
(b )过程与方法模仿秦九韶计算方法,体会古人计算构思的巧妙。
能根据排序法中的直接插入排序法与冒泡排序法的步骤,了解数学计算转换为计算机计算的途径,从而探究计算机算法与数学算法的区别,体会计算机对数学学习的辅助作用。
(c )情态与价值通过对秦九韶算法的学习,了解中国古代数学家对数学的贡献,充分认识到我国文化历史的悠久。
通过对排序法的学习,领会数学计算与计算机计算的区别,充分认识信息技术对数学的促进。
(2)教学重难点重点:1.秦九韶算法的特点2.两种排序法的排序步骤及计算机程序设计难点:1.秦九韶算法的先进性理解2.排序法的计算机程序设计(3)学法与教学用具学法:1.探究秦九韶算法对比一般计算方法中计算次数的改变,体会科学的计算。
2.模仿排序法中数字排序的步骤,理解计算机计算的一般步骤,领会数学计算在计算机上实施的要求。
教学用具:电脑,计算器,图形计算器(4)教学设想(一)创设情景,揭示课题我们已经学过了多项式的计算,下面我们计算一下多项式1)(2345+++++=x x x x x x f 当5=x 时的值,并统计所做的计算的种类及计算次数。
根据我们的计算统计可以得出我们共需要10次乘法运算,5次加法运算。
我们把多项式变形为:1)))1(1(1()(2+++++=x x x x x x f 再统计一下计算当5=x 时的值时需要的计算次数,可以得出仅需4次乘法和5次加法运算即可得出结果。
显然少了6次乘法运算。
这种算法就叫秦九韶算法。
(二)研探新知1.秦九韶计算多项式的方法01210123120132211012211)))((())(()()(a a x a x a x a a x a x a x a x a a x a x a x a x a a x a x a x a x a x f n n n n n n n n n n n n n n n n n n n +++++==+++++=+++++=+++++=--------------例1 已知一个5次多项式为8.07.16.25.325)(2345-+-++=x x x x x x f 用秦九韶算法求这个多项式当5=x 时的值。

《算法案例秦九韶算法》教学教案教学目标:1.理解秦九韶算法的原理和应用场景;2.掌握秦九韶算法的详细步骤;3.能够实现秦九韶算法的代码;4.能够对秦九韶算法进行分析和优化。
教学重点:1.秦九韶算法的原理和应用场景;2.秦九韶算法的详细步骤;3.秦九韶算法代码的实现。
教学难点:1.秦九韶算法的详细步骤;2.秦九韶算法代码的实现。
教学准备:1.讲义资料;2.演示程序;3.物理实例。
教学过程:一、导入(5分钟)教师利用一个简单的问题引入,例如:求多项式的值f(x)=2x^3+3x^2-5x+1,当x=2时,计算f(x)。
二、提问(5分钟)教师提问学生在计算多项式的值时的一般方法是什么,学生回答:将x的值代入多项式中的每一项并相加。
三、引入秦九韶算法(10分钟)教师引入秦九韶算法,并解释该算法可以大大减少计算量和运算时间的原理。
教师给出一个示例多项式f(x)=2x^3+3x^2-5x+1,当x=2时,计算f(x),并演示传统的计算方法和秦九韶算法的计算方法的对比。
四、秦九韶算法的详细步骤(20分钟)教师逐步讲解秦九韶算法的详细步骤:1.将多项式表达式改写成累加表达式,例如:f(x)=((2x+3)x-5)x+1;2.从内层开始计算并求解,逐步向外推算;3.计算每一层的累加结果,并将结果保存在一个变量中。
五、练习(15分钟)教师提供多个多项式表达式和对应的x值,让学生尝试用秦九韶算法计算结果,并对结果进行验证。
六、算法优化(15分钟)教师指导学生对秦九韶算法进行分析和优化,例如:是否存在重复计算的部分,可以通过建立一个字典来记录已经计算过的结果,以便在后续计算中直接使用。
七、总结(10分钟)教师帮助学生总结秦九韶算法的优点和适用场景,并与传统计算方法进行对比。
教学延伸:将秦九韶算法应用到实际问题中,例如多项式插值、图像处理等,并引导学生进行深入的研究和讨论。
教学反思:在教学过程中,要注意对秦九韶算法的详细步骤进行清晰的讲解,引导学生理解其原理和应用场景。

时案例2 秦九韶算法(一)导入新课思路1(情境导入)大家都喜欢吃苹果吧,我们吃苹果都是从外到里一口一口的吃,而虫子却是先钻到苹果里面从里到外一口一口的吃,由此看来处理同一个问题的方法多种多样.怎样求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值呢?方法也是多种多样的,今天我们开始学习秦九韶算法.思路2(直接导入)前面我们学习了辗转相除法与更相减损术,今天我们开始学习秦九韶算法.(二)推进新课、新知探究、提出问题(1)求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值有哪些方法?比较它们的特点.(2)什么是秦九韶算法?(3)怎样评价一个算法的好坏?讨论结果:(1)怎样求多项式f(x)=x5+x4+x3+x2+x+1当x=5时的值呢?一个自然的做法就是把5代入多项式f(x),计算各项的值,然后把它们加起来,这时,我们一共做了1+2+3+4=10次乘法运算,5次加法运算.另一种做法是先计算x2的值,然后依次计算x2·x,(x2·x)·x,((x2·x)·x)·x 的值,这样每次都可以利用上一次计算的结果,这时,我们一共做了4次乘法运算,5次加法运算.第二种做法与第一种做法相比,乘法的运算次数减少了,因而能够提高运算效率,对于计算机来说,做一次乘法运算所用的时间比做一次加法运算要长得多,所以采用第二种做法,计算机能更快地得到结果.(2)上面问题有没有更有效的算法呢?我国南宋时期的数学家秦九韶(约1202~1261)在他的著作《数书九章》中提出了下面的算法:把一个n次多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0改写成如下形式:f(x)=a n x n+a n-1x n-1+…+a1x+a0=(a n x n-1+a n-1x n-2+…+a1)x+ a0=((a n x n-2+a n-1x n-3+…+a2)x+a1)x+a0=…=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0.求多项式的值时,首先计算最内层括号内一次多项式的值,即v1=a n x+a n-1,然后由内向外逐层计算一次多项式的值,即v2=v1x+a n-2,v3=v2x+a n-3,…v n=v n-1x+a0,这样,求n次多项式f(x)的值就转化为求n个一次多项式的值.上述方法称为秦九韶算法.直到今天,这种算法仍是多项式求值比较先进的算法.(3)计算机的一个很重要的特点就是运算速度快,但即便如此,算法好坏的一个重要标志仍然是运算的次数.如果一个算法从理论上需要超出计算机允许范围内的运算次数,那么这样的算法就只能是一个理论的算法.(三)应用示例例1 已知一个5次多项式为f (x )=5x 5+2x 4+3.5x 3-2.6x 2+1.7x-0.8,用秦九韶算法求这个多项式当x=5时的值.解:根据秦九韶算法,把多项式改写成如下形式:f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8,按照从内到外的顺序,依次计算一次多项式当x=5时的值:v 0=5;v 1=5×5+2=27;v 2=27×5+3.5=138.5;v 3=138.5×5-2.6=689.9;v 4=689.9×5+1.7=3 451.2;v 5=3 415.2×5-0.8=17 255.2;所以,当x=5时,多项式的值等于17 255.2.算法分析:观察上述秦九韶算法中的n 个一次式,可见v k 的计算要用到v k -1的值,若令v 0=a n ,我们可以得到下面的公式:⎩⎨⎧=+==--).,,2,1(,10n k a x v v a v k n k kn Λ 这是一个在秦九韶算法中反复执行的步骤,因此可用循环结构来实现.算法步骤如下:第一步,输入多项式次数n 、最高次的系数a n 和x 的值.第二步,将v 的值初始化为a n ,将i 的值初始化为n-1.第三步,输入i 次项的系数a i .第四步,v=vx+a i ,i=i-1.第五步,判断i 是否大于或等于0.若是,则返回第三步;否则,输出多项式的值v. 程序框图如下图:程序:INPUT “n=”;nINPUT “an=”;aINPUT “x=”;xv=ai=n-1WHILE i>=0PRINT “i=”;iINPUT “ai=”;av=v*x+ai=i-1WENDPRINT vEND点评:本题是古老算法与现代计算机语言的完美结合,详尽介绍了思想方法、算法步骤、程序框图和算法语句,是一个典型的算法案例.变式训练请以5次多项式函数为例说明秦九韶算法,并画出程序框图.解:设f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0首先,让我们以5次多项式一步步地进行改写:f(x)=(a5x4+a4x3+a3x2+a2x+a1)x+a0=((a5x3+a4x2+ a3x+a2)x+a1)x+a0=(((a5x2+a4x+ a3)x+a2)x+a1)x+a0=((((a5x+a4)x+ a3)x+a2)x+a1)x+a0.上面的分层计算,只用了小括号,计算时,首先计算最内层的括号,然后由里向外逐层计算,直到最外层的括号,然后加上常数项即可.程序框图如下图:例2 已知n次多项式P n(x)=a0x n+a1x n-1+…+a n-1x+a n,如果在一种算法中,计算k x0(k=2,3,4,…,n)的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),那么计算P10(x0)的值共需要__________次运算.下面给出一种减少运算次数的算法:P0(x)=a0,P k+1(x)=xP k(x)+a k+1(k=0,1,2,…,n-1).利用该算法,计算P3(x0)的值共需要6次运算,计算P10(x0)的值共需要___________次运算.答案:65 20点评:秦九韶算法适用一般的多项式f(x)=a n x n+a n-1x n-1+…+a1x+a0的求值问题.直接法乘法运算的次数最多可到达2)1(nn,加法最多n次.秦九韶算法通过转化把乘法运算的次数减少到最多n次,加法最多n次.例3 已知多项式函数f(x)=2x5-5x4-4x3+3x2-6x+7,求当x=5时的函数的值.解析:把多项式变形为:f(x)=2x5-5x4-4x3+3x2-6x+7=((((2x-5)x-4)x+3)x-6)x+7.计算的过程可以列表表示为:最后的系数2 677即为所求的值.算法过程:v0=2;v1=2×5-5=5;v2=5×5-4=21;v3=21×5+3=108;v4=108×5-6=534;v5=534×5+7=2 677.点评:如果多项式函数中有缺项的话,要以系数为0的项补齐后再计算.(四)知能训练当x=2时,用秦九韶算法求多项式f(x)=3x5+8x4-3x3+5x2+12x-6的值.解法一:根据秦九韶算法,把多项式改写成如下形式:f(x)=((((3x+8)x-3)x+5)x+12)x-6.按照从内到外的顺序,依次计算一次多项式当x=2时的值.v0=3;v1=v0×2+8=3×2+8=14;v2=v1×2-3=14×2-3=25;v3=v2×2+5=25×2+5=55;v4=v3×2+12=55×2+12=122;v5=v4×2-6=122×2-6=238.∴当x=2时,多项式的值为238.解法二:f(x)=((((3x+8)x-3)x+5)x+12)x-6,则f(2)=((((3×2+8)×2-3)×2+5)×2+12)×2-6=238.(五)拓展提升用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x当x=3时的值.解:f(x)=((((((7x+6)+5)x+4)x+3)x+2)x+1)xv0=7;v1=7×3+6=27;v2=27×3+5=86;v3=86×3+4=262;v4=262×3+3=789;v5=789×3+2=2 369;v6=2 369×3+1=7 108;v7=7 108×3+0=21 324.∴f(3)=21 324.(六)课堂小结1.秦九韶算法的方法和步骤.2.秦九韶算法的计算机程序框图.(七)作业已知函数f(x)=x3-2x2-5x+8,求f(9)的值.解:f(x)=x3-2x2-5x+8=(x2-2x-5)x+8=((x-2)x-5)x+8 ∴f(9)=((9-2)×9-5)×9+8=530.。
§1.3秦九韶算法与排序(两个课时)教学目标:1了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
2掌握数据排序的原理能使用直接排序法与冒泡排序法给一组数据排序,进而能设计冒泡排序法的程序框图及程序,理解数学算法与计算机算法的区别,理解计算机对数学的辅助作用。
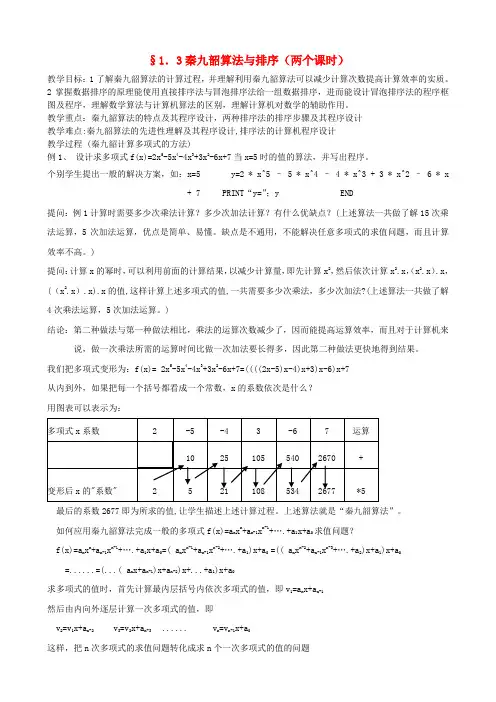
教学重点:秦九韶算法的特点及其程序设计,两种排序法的排序步骤及其程序设计教学难点:秦九韶算法的先进性理解及其程序设计,排序法的计算机程序设计教学过程 (秦九韶计算多项式的方法)例1、设计求多项式f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值的算法,并写出程序。
个别学生提出一般的解决方案,如:x=5 y=2 * x^5 – 5 * x^4 – 4 * x^3 + 3 * x^2 – 6 * x+ 7 PRINT“y=”;y END提问:例1计算时需要多少次乘法计算?多少次加法计算?有什么优缺点?(上述算法一共做了解15次乘法运算,5次加法运算,优点是简单、易懂。
缺点是不通用,不能解决任意多项式的求值问题,而且计算效率不高。
)提问:计算x的幂时,可以利用前面的计算结果,以减少计算量,即先计算x2,然后依次计算x2.x,(x2.x).x,((x2.x).x).x的值,这样计算上述多项式的值,一共需要多少次乘法,多少次加法?(上述算法一共做了解4次乘法运算,5次加法运算。
)结论:第二种做法与第一种做法相比,乘法的运算次数减少了,因而能提高运算效率,而且对于计算机来说,做一次乘法所需的运算时间比做一次加法要长得多,因此第二种做法更快地得到结果。
我们把多项式变形为:f(x)= 2x5-5x4-4x3+3x2-6x+7=((((2x-5)x-4)x+3)x-6)x+7从内到外,如果把每一个括号都看成一个常数,x的系数依次是什么?用图表可以表示为:最后的系数2677即为所求的值,让学生描述上述计算过程。

1.3算法案例:秦九韶算法1、利用秦九韶算法求多项式1153723+-+x x x 在23=x 的值时,在运算中下列哪个值用不到( )A 、164B 、3767C 、86652D 、851692、利用秦九韶算法计算多项式1876543x f(x)23456++++++x x x x x = 当x=4的值的时候,需要做乘法和加法的次数分别为( )A 、6,6B 、5,6C 、5,5D 、6,53、利用秦九韶算法求多项式1352.75.38123)(23456-++-++=x x x x x x x f 在6=x 的值,写出详细步骤。
4、下图的框图是一古代数学家的一个算法的程序框图,它输出的 结果s 表示( )A 、3210a a a a +++的值B 、300201032x a x a x a a +++的值 C 、303202010x a x a x a a +++的值 D 、以上都不对5、已知n 次多项式1011()n n n n n P x a x a x a x a --=++++,如果在一种算法中,计算0k x (k =2,3,4,…,n )的值需要k -1次乘法,(1)计算30()P x 的值需要9次运算(6次乘法,3次加法),那么计算0()n P x 的值需要多少次运算?(2)若采取秦九韶算法:0011(),()()k k k P x a P x xP x a ++==+(k =0, 1,2,…,n -1),计算30()P x 的值只需6次运算,那么计算0()n P x 的值共需要多少次运算?(3)若采取秦九韶算法,设a i =i+1,i=0,1,…,n ,求P 5(2)(写出采取秦九韶算法的计算过程)答案:1、D2、A3、解:13)5)2.7)5.3)8)123((((()(-++-++=x x x x x x x f2.243168)6(2.2431681362.40530562.67542.765.11245.36188863012635645342312010==-⨯==+⨯==+⨯==-⨯==+⨯==+⨯==f v v v v v v v v v v v v v4、C5、n +3)(2)2n ;(3)∵0011(),()()k k k P x a P x xP x a ++==+,∴P0(2)=1,P1(2)=2P0(2)+2=4;P2(2)=2P1(2)+3=11;P3(2)=2P2(2)+4=26;P4(2)=2P3(2)+5=57;P5(2)=2P4(2)+6=120。
1.3 案例2 秦九韶算法一、基本信息设计者:***学生:*****教材:人教版,必修3第一章“算法初步”的第3节“算法案例”中的秦九韶算法。
二、教材分析为解决一个问题而采取的方法和步骤,称为算法。
算法是数学的重要组成部分,是计算机理论和技术的基础。
随着现代信息技术的飞速发展,算法思想已经成为现代人应具备的一种数学素养,新课标已将算法列为高中数学的必修内容。
秦九韶算法既能体现新课程、新理念、新课标,又可以结合旧知识,调动学生的积极性,培养学生的自主探索能力及学习兴趣。
三、学情分析从学生的认知基础看,学生在已经学习了程序框图、算法语句的相关知识,积累了研究算法的基本方法与初步经验。
学生的基础较好,能够在一节课中掌握框图和算法语句。
从学生的思维发展看,高二学生思维能力正在由形象经验型向抽象理论型转变,能够用假设、推理来思考和解决问题。
但是,学生看待问题还是静止的、片面的,抽象概括能力比较薄弱,这对建构秦九韶算法中的循环结构有一定的困难。
四、教学目标【知识与技能】1、了解秦九韶算法的计算过程。
2、理解利用秦九韶算法可以减少计算次数提高计算效率的实质。
【过程与方法】1、模仿秦九韶计算方法,体会古人计算构思的巧妙。
2、了解数学计算转换为计算机计算的途径,从而探究计算机算法与数学算法的区别,体会计算机对数学学习的辅助作用。
【情感、态度与价值观】1、通过对秦九韶算法的学习,了解中国古代数学对世界数学发展的贡献,充分认识到我国文化历史的悠久。
2、通过对秦九韶算法的广泛应用、丰富其联想的空间,懂得“来龙去脉”。
3、充分认识信息技术对数学的促进。
五、教学重点和难点重点:理解秦九韶算法的思想。
难点:用循环结构表示算法步骤。
六、教学方法学生探究、教师引导。
七、教学流程八、教学过程1、逐渐渗透算法意识,为算法学习铺路【思考1】求当5x = 时多项式5432()1f x x x x x x =+++++的值。
学生自己提出一般的解决方案:将5x =代入多项式进行计算即可。
〔教案〕1.3 算法案例――-秦九韶算法
教学目标:
(1)在学习中国古代数学中的算法案例的同时,进一步体会算法的特点。
(2)体会中国古代数学对世界数学发展的贡献。
教学重点和难点
(1)重点:理解秦九韶算法的思想。
(2)难点:用循环结构表示算法的步骤。
教学基本流程
(1)设计算法,求具体多项式的值
(2)改进算法,提高运算效率
(3)介绍秦九韶算法,求一般多项式的值
(4)用循环结构表示秦九韶算法的关键步骤
(5)对秦九韶算法和算法本身的特点进行小结
教学情景设计
一、新课引入
在数学的发展史上,从公元前2、3世纪公元14世纪,中国的数学虽有过高潮,也有过低落,但一直走在世界的前列,是世界数学的中心。
中国古代数学对世界数学发展有着不可磨灭的贡献。
秦九韶算法就是中国古代数学的一枝奇葩。
今天这节课我们领略秦九韶算法的魅力。
二、问题设计。