北京理工大学信号与系统考研真题1996

826北京理工大学信号处理导论一、考试内容1、信号与系统部分信号与系统以确定性信号经过线性时不变〔LTI〕系统的传输与处理为主线，构建起一套根本概念和根本分析与处理方法，从时域到变换域，从连续到离散，从输入输出描绘到状态空间描绘。

考生应掌握如下根本概念、理论和方法:(1)信号、系统的根本概念：信号描绘及波形运算，根本典型信号。

系统模型、互联及主要特性；(2)LTI系统的时域分析：卷积积分、卷积和、卷积性质与计算。

用微分/差分方程描绘的因果系统的经典解法。

零输入/零状态响应；(3)确定信号的频谱分析：周期信号的傅立叶级数及傅立叶变换。

非周期信号的傅立叶变换及其性质，典型信号的傅立叶变换及其频谱表示。

抽样定理；(4)LTI系统的频域分析：系统频率响应，系统的傅立叶分析法。

系统模与相位表示、波特图。

无失真传输条件，理想滤波器；(5)LTI系统的复频域分析：拉氏变换，Z变换。

典型信号的变换对。

用单边拉氏变换和Z变换求解微分/差分方程。

系统函数。

系统方框图；(6)系统状态空间分析：状态方程与输出方程的建立。

掌握状态方程的一种解法。

多输入－多输出系统稳定性判别。

2、数字信号处理部分数字信号处理在全面掌握信号与系统知识的根底上，针对确定性离散信号构建起一套从连续到离散，从时域到变换域的根本概念和根本分析与处理方法。

考生应掌握如下根本概念、理论和方法:(1)全面掌握信号与系统的根底知识；(2)离散傅立叶变换〔DFT〕：DFT定义、性质；频率取样；用DFT对连续时间信号逼近；加权技术与窗函数；(3)快速傅立叶变换〔FFT〕：基－2按时间/按频率抽取的FFT算法；N为复合数的FFT算法；分裂基FFT算法；实序列的FFT算法；快速FFT的应用；(4)数字滤波器〔DF〕：IIR/FIR DF的根本构造；IIR DF的设计〔原理、常用模拟低通滤波器的特性、从模拟滤波器设计数字滤波器的方法〕；FIR DF的设计〔原理、线性相位FIR DF 的特点、窗函数设计法和频率取样设计法〕；IIR和FIR DF的比较。

北京理工大学信息科学技术学院自动控制理论1999——2000，2002——2008自动控制理论（非控类）2004电子技术（含模拟、数字部分）1999——2000，2002——2008模拟电子技术与数字电子技术2000——2002模拟与数字电路1999——2000，2002微机控制与应用技术2002——2008控制工程基础2003——2008物理光学2003——2004，2007——2008应用光学1999——2008，2010（2010为回忆版）波动光学2002大学物理2006——2008精密机械设计2003——2008（其中2003年称“精密机械基础”）激光原理1999——2001，2005——2008电子电路2003——2005，2007——2008电路分析基础1999——2000信号处理导论2003——2008信号与系统1996——2002半导体物理学1999——2008电磁场理论1999——2000，2002——2008微机原理及应用2004——2005电动力学2003——2004理论力学1996——2008（96——98非原版）生物化学1999——2008（注：2007年试卷共11页，缺P5-6页）生物化学（A）2005——2006，2008计算机专业基础（含计算机组织与结构、数据结构）2007计算机技术基础（含计算机组成原理、操作系统和数据结构）2003——2006计算机原理（含操作系统）1999——2002程序设计1999——2000计算机系统结构基础（含计算机组成原理、计算机网络和数据结构）2004——2005 软件理论基础（含离散数学、操作系统、数据结构）1999——2005数据结构与程序设计2004——2008微波技术基础1999——2000晶体管理原理与制造1999——2000机电工程学院电子技术（含模拟、数字部分）1999——2000，2002——2008电子技术基础2007——2008自动控制理论1999——2000，2002——2008自动控制理论（非控类）2004电磁学2005——2008量子力学2005——2008运筹学2001——2008工程力学基础2007——2008流体力学基础2006工程流体力学2005数学物理方程2002——2006数学物理方法2000材料力学1997——1999，2002——2008理论力学1996——2008（96——98非原版）电动力学2003——2004微机控制与应用技术2002——2008控制工程基础2003——2008精密机械设计2003——2008（其中2003年称“精密机械基础”）应用光学1999——2008，2010（2010为回忆版）波动光学2002微机原理及应用2004——2005有机化学1997——2008无机化学（A）2003——2007无机化学（B）2003——2005，2007——2008分析化学2003——2008分析化学(A)2006物理化学2003——2008高分子物理2005——2008高分子化学及高分子物理2003——2004安全系统工程2003——2005，2008工程热力学（不含传热学）2003——2008爆炸与安全技术2005爆炸及其作用2006爆轰理论2003——2005化学2002——2005传感与测试技术2004——2005算法语言1998微波技术基础1999——2000晶体管理原理与制造1999——2000传热学2000应用电子技术2004机械与车辆工程学院电子技术（含模拟、数字部分）1999——2000，2002——2008 电子技术基础2007——2008自动控制理论1999——2000，2002——2008自动控制理论（非控类）2004机械设计2001——2008机械设计原理2001机械制造工程基础2003——2008机械制造工艺学2002理论力学1996——2008（96——98非原版）微机控制与应用技术2002——2008应用光学1999——2008，2010（2010为回忆版）电路分析基础1999——2000模拟电子技术与数字电子技术2000——2002模拟与数字电路1999——2000，2002精密机械设计2003——2008（其中2003年称“精密机械基础”）控制工程基础2003——2008微机原理及应用2004——2005工程热力学（不含传热学）2003——2008物理化学2003——2008工程力学基础2007——2008流体力学基础2006工程流体力学2005交通运输系统工程学2005，2007——2008微波技术基础1999——2000晶体管理原理与制造1999——2000数字电路与数字信号处理2008材料科学与工程学院物理化学（A）2008高分子物理2005——2008高分子化学及高分子物理2003——2004材料科学基础2003——2007材料力学1997——1999，2002——2008普通化学2008综合化学2008有机化学1997——2008无机化学（A）2003——2007无机化学（B）2003——2005，2007——2008分析化学2003——2008分析化学(A)2006理论力学1996——2008（96——98非原版）电化学原理2003——2006微波技术基础1999——2000晶体管理原理与制造1999——2000化工与环境学院自动控制理论1999——2000，2002——2008自动控制理论（非控类）2004过程控制原理2000——2005，2007——2008化工原理2002——2008有机化学1997——2008无机化学（A）2003——2007无机化学（B）2003——2005，2007——2008分析化学2003——2008分析化学(A)2006物理化学2003——2008电化学原理2003——2006环境微生物学2007——2008工程热力学（不含传热学）2003——2008微波技术基础1999——2000晶体管理原理与制造1999——2000生命科学与技术学院生物化学1999——2008（注：2007年试卷共11页，缺P5-6页）生物化学（A）2005——2006，2008分析化学2003——2008分析化学(A)2006细胞生物学2004——2006微生物学2005——2008分子生物学2007——2008有机化学1997——2008无机化学（A）2003——2007无机化学（B）2003——2005，2007——2008药理学2007信号处理导论2003——2008信号与系统1996——2002电子电路2003——2005，2007——2008物理光学2003——2004，2007——2008应用光学1999——2008，2010（2010为回忆版）波动光学2002信号理论基础2007——2008计算机专业基础（含计算机组织与结构、数据结构）2007计算机技术基础（(含计算机组成原理、操作系统和数据结构）2003——2006计算机原理（含操作系统）1999——2002程序设计1999——2000计算机系统结构基础（含计算机组成原理、计算机网络和数据结构）2004——2005 软件理论基础（含离散数学、操作系统、数据结构）1999——2005数据结构与程序设计2004——2008理学院电子技术（含模拟、数字部分）1999——2000，2002——2008大学物理2006——2008数学分析1995，1999——2000，2003——2008高等代数2003——2008电磁学2005——2008量子力学2005——2008电动力学2003——2004普通化学2008综合化学2008无机化学（A）2003——2007无机化学（B）2003——2005，2007——2008分析化学2003——2008分析化学(A)2006物理化学（A）2008物理化学2003——2008有机化学1997——2008理论力学1996——2008（96——98非原版）材料力学1997——1999，2002——2008工程热力学（不含传热学）2003——2008数学物理方程2002——2006数学物理方法2000电路分析基础1999——2000模拟电子技术与数字电子技术2000——2002模拟与数字电路1999——2000，2002激光原理1999——2001，2005——2008微机控制与应用技术2002——2008爆炸与安全技术2005爆炸及其作用2006电化学原理2003——2006工程力学基础2007——2008流体力学基础2006工程流体力学2005微波技术基础1999——2000晶体管理原理与制造1999——2000管理与经济学院宏微观经济学2008管理学2003——2008（2003，2004名称叫做“管理学基础”。

目录目录 (1)复习题一 (2)答案 (4)复习题二 (8)答案 (13)复习题三 (25)答案 (40)复习题四 (71)答案 (72)复习题五 (74)答案 (81)复习题六 (96)答案 (97)复习题七 (99)复习题八 (108)复习题一1.1 选择题（每小题可能有一个或几个正确答案，将正确的题号填入[ ]内） 1．f （5-2t ）是如下运算的结果————————（ ） （1）f （-2t ）右移5 （2）f （-2t ）左移5 （3）f （-2t ）右移25 （4）f （-2t ）左移251.2 是非题（下述结论若正确，则在括号内填入√，若错误则填入×） 1．偶函数加上直流后仍为偶函数。

（ ）2. 不同的系统具有不同的数学模型。

（ ）3. 任何信号都可以分解为偶分量与奇分量之和。

（ ） 4．奇谐函数一定是奇函数。

（ ） 5．线性系统一定满足微分特性 （ ）1.3 填空题1．=⋅t t cos )(δ=+t t 0cos )1(ωδ=-⋅)(cos )(0τωδt t=--)2()cos 1(πδt t=--⎰∞∞-dt t t )2()cos 1(πδ ⎰+∞∞-=⋅tdt t cos )(δ⎰+∞∞-=tdt t 0cos )(ωδ ⎰∞-=td ττωτδ0cos )(⎰+∞∞-=+tdt t 0cos )1(ωδ⎰∞-=+td ττωτδ0cos )1(2．=⋅-at e t )(δ=⋅-t e t )(δ⎰∞--=td e ττδτ)(⎰∞∞--=--dt t e t t )1(][22δ⎰∞∞--=dt e t at )(δ1.4 简答题1．画出题图一所示信号f （t ）的偶分量f e （t ）与奇分量f o （t ）。

图一2．)(t f 如图二所示，试画出)(t f 的偶分量)(t f e 和奇分量()o f t 的波形。

t图二3．某线性时不变系统在零状态条件下的输入e （t ）与输出r （t ）的波形如题图三所示，当输入波形为x （t ）时，试画出输出波形y （t ）。

1 ．按照信号的能量或功率为有限值，信号可分为和。

2 ．一个离散时间系统可由、、等基本部件组成。

3 ．如图所示 LTIS ，若, , ，则系统的输出为。

4 ．应用卷积积分的方法可以得到系统的。

5 ．6 ．试写出下列函数的频谱密度函数(a) , 所以(b) , 所以7. x(n) 的离散时间傅立叶变换为 X(e ), 则 y(n)= 的傅立叶变换为8. 果而稳定的 LTI 系统，单位冲击响应为 h(t) , 系统 H(s) 有一极点在s= -2, 则是9. 知一因果而稳定系统的单位脉冲响应为 h(n),H(z) 是有理的，且, 则10 ．二、计算题1 ．设三个因果 LTI 系统的级联如图 1 所示，其中冲激响应而总的冲激响应如图 2 所示，求(a)冲激响应(b) 整个系统对输入的响应2 ．考虑一个 LTI 系统它对输入的响应为(a) 求该系统的频率响应(b) 确定该系统的冲激响应(c) 求出联系输入、输出的微分方程，并用积分器、相加器和系数相乘器实现该系统。

3 ．如图所示，系统(1) 以为状态变量列出其状态方程与输出方程(2) 求状态转移矩阵４．的单边拉氏反变换５．已知信号 x(n) 的傅立叶变换, 求的傅立叶反变换试题一答案一. 填空题1 ．答案：（能量信号，功率信号）2 ．答案：（单位延时器、相加器、倍乘器）3 ．4 ．答案：（零状态响应）5 ．答案：6 ．答案：(a)7.8.9.10 ．二、计算题1 ．答案：2 ．解 :(a)(b)(c)3 ．解 :(1)(2)４．解：（分子阶次与分母阶次相同，降阶）（分母多项式带有重根的部分分式展开法）又因为求单边拉氏变换所得信号为因果信号５．解：（注：文档可能无法思考全面，请浏览后下载，供参考。

）。

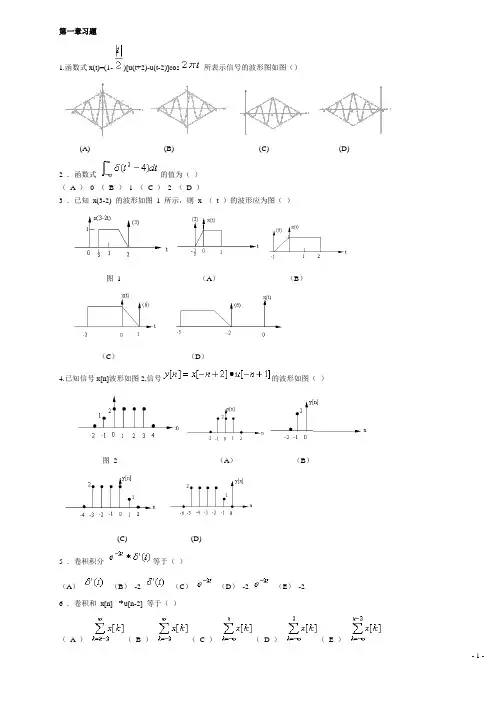
第一章习题1.函数式x(t)=(1-)[u(t+2)-u(t-2)]cos所表示信号的波形图如图（）(A) (B) (C) (D)2 ．函数式的值为（）（ A ）0 （B ）1 （ C ） 2 （D ）3 ．已知x(3-2) 的波形如图1 所示，则x （t ）的波形应为图（）图1 （A）（B）（C）（D）4.已知信号x[n]波形如图2,信号的波形如图（）图2 （A）（B）(C) (D)5 ．卷积积分等于（）（A）（B）-2 （C）（D）-2 （E）-26 ．卷积和x[n] u[n-2] 等于（）（ A ）（ B ）（ C ）（ D ）（ E ）7 ．计算卷积的结果为（）（ A ）（B ）（ C ）（D ）8 ．已知信号x(t) 的波形如图3 所示，则信号的波形如图（）图3 （A）(B)(C) (D) 题九图9 ．已知信号x （t ）如图所示，其表达式为（）(A) (B)(C) (D)10 ．已知x（t)为原始信号，y(t)为变换后的信号,y(t) 的表达式为（）（ A ）（B ）（ C ）（D ）11 ．下列函数中（）是周期信号（ A ）（B ）（ C ）（ D ）（ E ）12 ．函数的基波周期为（）。

（ A ）8 （B ）12 （C ）16 （ D ）2413 ．某系统输入—输出关系可表示为，则该系统是（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（D ）因果（ E ）稳定14 ．某系统输入—输出关系可表示为，则系统为（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（D ）因果（ E ）稳定15．某系统输入—输出关系可表示为,则系统为（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（D ）因果（ E ）稳定16.某系统输入—输出关系可表示为，则系统为（）系统。

（ A ）线性（ B ）时不变（ C ）无记忆（D ）因果（ E ）稳定17 ．某系统输入—输出关系可表示为，则系统为（）系统（ A ）线性（ B ）时不变（ C ）无记忆（D ）因果（）稳定18 ．下列系统中，（）是可逆系统（A）y[n]=nx[n] （B）y[n]=x[n]x[n-1] （C）y(t)=x(t-4) （D）y(t)=cos[x(t)] （E ）y[n]=19 ．如图系统的冲激响应为（）（ A ）（ B ）（ C ）（D ）20 ．某系统的输入x （t ）与输出y （t ）之间有如下关系，则该系统为（）（A）线性时变系统（B）线性非时变系统（C）非线性时变系统（D）非线性非时变系统21 ．一个LTI 系统在零状态条件下激励与响应的波形如图，则对激励的响应的波形（）(A) (B) (C) (D)22. 线形非时变系统的自然（固有）响应就是系统的（）（ A ）零输入响应（ B ）原有的储能作用引起的响应（ C ）零状态响应（D ）完全的响应中去掉受迫（强制）响应分量后剩余各项之和23 ．零输入响应是（）（ A ）全部自由响应（ B ）部分零状态响应（ C ）部分自由响应（ D ）全响应与强迫响应之差24 ．下列叙述或等式正确的是（）(A) (B)(C)若,则(D)x(t) 和h(t) 是奇函数，则是偶函数25.设是一离散信号,,,则下列说法( )是正确的(A) 若是周期的，则也是周期的(B) 若是周期的，则也是周期的(C) 若是周期的，则也是周期的(D) 若是周期的，则也是周期的26 ．有限长序列经过一个单位序列响应为的离散系统，则零状态响应为（）(A) (B)(C) (D)第二章习题1. 某LTI 连续时间系统具有一定的起始状态，已知激励为x （t ）时全响应，t 0 ，起始状态不变，激励为时，全响应y （t ）＝7e ＋2e ，t 0 ，则系统的零输入响应为（）（ A ）（ B ）（ C ）（D ）2 ．微分方程的解是连续时间系统的（）(A) 零输入响应(B) 零状态响应(C) 自由响应(D) 瞬态响应（E）全响应3 ．单位阶跃响应是（）(A) 零状态响应(B) 瞬态响应(C) 稳态响应(D) 自由响应(E) 强迫响应4 ．已知系统如图所示，其中h (t) 为积分器，为单位延时器，h (t) 为倒相器，则总系统的冲激响应h (t) 为（）（ A ）（ B ）（ C ）（D ）5 ．如图所示电路以为响应，其冲激响应h (t) 为（）(A) (B)(C) (D)6. 某LTI 系统如图所示，该系统的微分方程为（）(A ) (B)(C) (D)7 ．已知系统的微分方程, 则求系统单位冲激响应的边界条件h(0 ) 等于（）(A) －1 (B) 0 (C) 2 (D) ＋18 ．已知系统的微分方程则系统的单位冲激响应为（）(A) (B) (C) (D)9 ．已知描述系统的微分方程和初始状态0 值如下；y (0 ) ＝2 ，, , ，则初始条件0 值为（）(A) (B)(C) (D)10 ．已知描述系统的微分方程和初始状态0 值如y(t) ＋6 y (t) ＋8 y (t) ＝x (t) ＋2x (t) ，y (0 ) ＝1 ，y (0 ) ＝2 ，x (t) ＝（t ）则初始条件0 值为（）。

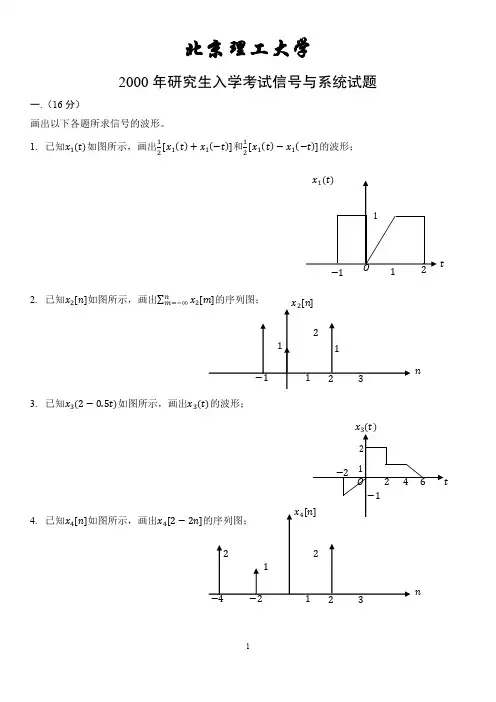
北京理工大学2000年研究生入学考试信号与系统试题一.（16分）画出以下各题所求信号的波形。

1. 已知x 1(t)如图所示，画出12[x 1(t )+x 1(−t )]和12[x 1(t )−x 1(−t )]的波形；2. 已知x 2[n]如图所示，画出∑x 2[m]n m=−∞的序列图；3. 已知x 3(2−0.5t)如图所示，画出x 3(t)的波形；4. 已知x 4[n]如图所示，画出x 4[2−2n]tnx 2[n]1 21 123−1二．（17分）已知如图所示电路系统，其中R1=2kΩ，R2=1kΩ，C=1500μF，输入信号f(t)如图所示，求输出电压v C(t)。

1.首先使用时域分析法求解v C(t)的单位冲激响应h(t)；2.然后用时域卷积积分法和频域傅里叶变换法求出在输入信号f(t)作用下的v C(t)表达式，并概略画出v C(t)的波形。

+v C(t)−三．（17分）已知系统框图如图所示，其中x1(t)=sin100tπtx2(t)=T∑δ(t−nT)∞n=−∞1.画出x1(t)和x2(t)的频谱图；2.在如图(a)所示系统中，若要求y(t)=x1(t−0.03)，试确定x2(t)的周期T及框图中H(jω)；3.在如图(b)所示系统中，若要求y(t)=x1(t)，试确定x2(t)的周期T及框图中H(jω)；)四.（16分）已知如图所示离散时间函数x [n ]。

1. 求x [n ]的离散时间傅里叶变换X [Ω]；2. 以周期N=10，把x [2n ]开拓成一个周期信号x̅[2n ]。

(1) 画出周期信号x̅[2n ]的波形图；(2) 把x̅[2n ]展开成为离散傅里叶级数，并画出频谱图； (3) 若把周期信号x̅[2n ]通过一个单位抽样响应ℎ[n ]=sinπn 2πn的系统，求此系统的输出响应y [n ]。

nx[n] 121 −21 1234五．（17分）如图所示电路系统，R =1Ω，L =0.5H ，C =1.6F 。

2016年826信号与系统部分一、简答（5×6=30分）1.物理上是否存在这样的信号，既持续时间有限，又频带宽度有限？说出理由2.)(x t 如下图，画出)15.-0(x +t 的波形3.一个线性时不变系统，初试时刻无储能，当输入)(1t x 为单位阶跃信号，即)()(1t u t x =时，系统的输出为)(2)()(y 21t t u e t t δ+=-，试通过时域方法计算输入为)()(x 2t u e t t -=时，系统的零状态响应)(y 2t 4.计算)]([)(x )1(3t u e dtd t t --=的傅立叶变换)(ΩX 5.如图所示系统，输入为)(x t，输出为)(y t ，该系统的三个子系统的单位冲激响应分别为)(h 1t ，)(h 2t ，)(h 3t ，其中)(u )(h 1t t =，)()(h 3t t δ=，)(h 2t 由微分方程)(2)(2)(y 11'1t x t y t =+ 确定。

试利用拉普拉斯变换求该系统的系统函数)(s H 和单位冲激响应)(h t二、（25分）两种调制器如下图所示。

图中，输入信号)(x t频谱)(ΩX 、系统)(ΩM H 的单位冲激响应)(h m t 、)(p 1t 和)(p 2t 的波形分别如图a 、b 、c 、d 所示，且T10<<Ω，T <<τ（1）（15分）试画出已调信号)(y 1t 和)(y 2t 的频谱)(1ΩY 和)(2ΩY ，并说明)(1ΩY 和)(2ΩY 有何区别（2）（10分）试判断能否在接收端通过滤波器)(1ΩH 和)(2ΩH 分别恢复出信号)(x t 。

若能恢复，设计给出)(1ΩH 和)(2ΩH 。

若不能恢复，请给出理由三、（20分）已知一个系统的结构如图a ，输入信号)(x t的频谱)(ΩX 、理想低通滤波器频率响应)(ΩH 和周期信号)(p t 的波形分别如b 、c 、d 所示（1）（12分）分别画出图a 中A B C D 处的信号频谱（2）（8分）如果上述系统中信号)(p t 的周期改为原周期的一半，画出D 处的频谱四、（15分）图为一个线性系统模型，假设已知该反馈系统是稳定的，试证明若)z (H 在z=1处有极点，则该系统能够跟踪输入单位阶跃序列)()(x n u n =，即0)]()([lim n =-+∞→n x n y数字信号处理部分一、简答（20分）1.（5分）已知信号)1(*)3()(21+-+=n x n x n y ，其中)()21()(1n u n x n =，)()41()(2n u n x n=，利用Z 变换性质求)(n y 的Z 变换)(Z Y 2.（5分）已知序列)3()1()(2)(-+-+=n n n n x δδδ的5点DFT 为)(k X ，求)()(2k X k Y =的DFT 的逆变换)(n y 3.（4分）设实连续信号是频率为12.85Hz 的正弦信号，现用100Hz 的采样频率对其进行采样，并利用N=1000点DFT 分析信号的频谱。

一个《信号与系统》考了147分的考研者的经历信号与系统我考了147，总分438！我考的成绩挺平均：政治83，英语，77，数学131，专业课信号与系统147分，总分438。

但我在这里不说别的，只说说我复习专业课的经验。

由于我工作很不顺心，所以才有了考研的想法，本来打算边工作边考。

后来在一次老同学的聚会上，原来的同学有几个关系好的鼓励我要好好复习。

所以我就下了决心辞去了工作考，因此复习时我特别认真和重视，下定决心要比别人付出双倍时间和金钱。

我在六月初买了专业课的课本和参考书，然后利用公司的上网条件搜集到了我要用得的资料（这个工作确实太花时间，我几乎用了整整三个月天天趴在网上搜集，对工作影响大了，老板批评了我几次，后来在老板炒我鱿鱼之前我先交了辞职书了）我在7月以前是利用空闲时间学习，主要看了上海交大胡光锐和中科大徐守时的信号与系统，还有北理工的数字信号处理，然后决定先学信号与系统后学数字信号处理。

7月后就抓紧一切可以利用的时间学习了，甚至上班也偷偷看。

用一个月细读了清华大学郑均理信号与系统上下二册，并对照答案看过了大多数课后题（第一版的课后题包含了全部第二版的课后题，因此第一版的答案可以用）。

8月结合笔记细读了西安交大刘树堂翻译的奥本海姆的信号与系统，并对照答案做课后题（也是用第一版的答案，题号要自己找）。

这本书不愧为经典，后悔没早点看。

课后题基础题没做，提高题几乎全作了，有一些明显不像考试题得只看了看答案的思想。

用时一个月。

9月先把上交胡光锐的解题指导，和张小虹的学习指导与实践的例题看完了，用时15天。

然后开始做第一次作试卷，做了8份杂的+上交大7份+中科大的11份，受打击极大，不过还是硬着头皮挑会做得先做了，留下了不会的和所有的数字信号处理的题。

这个时候是我第一次也是唯一一次产生放弃的念头。

我的感谢我在母校上研的老同学们，是他们的鼓励让我坚定了一定要坚持到底的信念。

10月开始辞职在家全力复习，从10月1号开始做西安交大的15份卷子，感觉能做的题目占到了一半。