实验三 函数的应用

一、实验目的1. 理解函数的概念及其应用。

2. 掌握函数的基本性质和运算。

3. 应用函数解决实际问题。

4. 提高数学思维能力和解决问题的能力。

二、实验内容本次实验主要围绕以下内容展开：1. 函数的定义及性质2. 常见函数的图像和性质3. 函数的运算4. 函数在实际问题中的应用三、实验步骤1. 函数的定义及性质（1）首先，我们学习了函数的定义：设A、B是两个非空数集，如果按照某种确定的对应关系f，使得对于集合A中的任意一个数x，在集合B中都有唯一确定的数y与之对应，则称这种对应关系f为从集合A到集合B的一个函数，记作f：A→B。

（2）接着，我们探讨了函数的基本性质，如单调性、奇偶性、周期性等。

（3）最后，我们分析了函数的图像，了解函数图像与函数性质之间的关系。

2. 常见函数的图像和性质（1）我们学习了幂函数、指数函数、对数函数、三角函数等常见函数的图像和性质。

（2）通过绘制函数图像，我们观察了函数的增减性、对称性、周期性等特征。

（3）我们掌握了如何根据函数图像分析函数性质的方法。

3. 函数的运算（1）我们学习了函数的加法、减法、乘法、除法、复合等基本运算。

（2）通过练习，我们熟练掌握了函数运算的技巧。

（3）我们了解了函数运算在实际问题中的应用。

4. 函数在实际问题中的应用（1）我们学习了如何利用函数解决实际问题，如优化问题、增长率问题等。

（2）通过实例分析，我们掌握了函数在实际问题中的应用方法。

（3）我们提高了运用数学知识解决实际问题的能力。

四、实验结果与分析1. 函数的定义及性质通过实验，我们掌握了函数的定义和基本性质，如单调性、奇偶性、周期性等。

同时，我们了解了函数图像与函数性质之间的关系。

2. 常见函数的图像和性质通过绘制函数图像，我们直观地观察了函数的增减性、对称性、周期性等特征。

这有助于我们更好地理解函数的性质。

3. 函数的运算通过练习，我们熟练掌握了函数的加法、减法、乘法、除法、复合等基本运算。

实验三函数的应用实验三函数的应用实验3函数的应用(2学时)一、实验目的1．掌握函数的定义和调用方法。

2．练习重载函数的使用。

3．练习函数模板的使用。

4．练习使用系统函数。

5.学习使用VC++的调试功能，并使用stepinto跟踪到该功能的内部。

二、实验任务1.编写函数将华氏温度转换为摄氏温度，转换公式为。

C=（f-32）*5/9。

2.编写重载函数maxl，可以分别计算两个整数、三个整数、两个双精度数和三个双精度数的最大值。

3．使用重载函数模板重新实现上小题中的函数maxl。

4.使用系统函数pow（x，y）计算Zi的值。

请注意，其中包括头文件mathh。

5.用递归方法编写函数，计算斐波那契级数，观察递归调用过程。

三、实验步骤1.编写函数floatconvert（floatmpfer），参数和返回值为float类型，实现算法C=（f-32）*5/9，在main（）函数中实现输入和输出。

程序名称：lab3_1。

cpp2．分别编写四个同名函数maxl，实现函数重载，在main()函数中测试函数功能。

程序名：lab3_2．cpp。

3.使用函数模板查找任何类型的最大数量。

对于不同数量的参数，编写两个同名函数模板maxl。

参数个数不同，实现函数重载，并在main（）函数中测试函数。

程序名称：lab3_3.cpp4．在main()函数中提示输入两个整数x、y，使用cin语句得到x、y的值，调用pow(x，y)函数计算x的y次幂的结果，再显示出来。

程序名．1ab3_4.cpp。

5．编写递归函数intfib(intn)，在主程序中输入n的值，调用fib函数计算斐波那契级数。

公式为FIB（n）=FIB（n-1）+FIB（n-2），n>2；fib（1）=fib（2）=1.使用if语句判断函数的退出，使用cout语句在程序中输出提示信息。

程序名称：lab3_5.cpp6．使用debug中的stepinto追踪到函数内部，观察函数的调用过程，参考程序如下：／lab3_5#includeintfib(intn)；intmain(){intn，回答cout<cin>>ncout<库特<intfib(int，n){库特<cout<{cout<7.调试步骤如下：(1)选择菜单命令build|startdebug|stepin，或按下快捷键fll，系统进入单步执行状态，程序开始运行，并出现一个dos窗口，此时visualstudio中光标停在main()函数的入口处。

实验三窗函数的特性分析窗函数是在时间域上对信号进行加权的一种方法。

它在信号处理领域中应用广泛，用于去除频谱泄露和减少频谱波动。

窗函数可以改变信号的频谱特性，有助于减小频谱波动，提高频谱分析的准确性。

本实验将分析三种不同类型的窗函数：矩形窗、汉明窗和布莱克曼窗。

1.矩形窗：矩形窗是一种简单的窗函数，它将输入的信号乘以常数1、它在时间域上呈现出矩形的形状，频域上表现为sinc函数。

矩形窗的特点是具有较宽的主瓣，但是有很高的边瓣衰减，对于频谱泄露较为敏感。

它适用于信号频谱比较窄的情况，可以提供较好的分辨率。

2.汉明窗：汉明窗是一种平滑且对称的窗函数，它在时间域上具有一对对称的凸边，频域上表现为sinc-squared函数。

汉明窗的特点是在频域上拥有较窄的主瓣和较小的边瓣泄露。

这使得它在频谱分析中具有较好的分辨率和较低的波动。

它适用于信号频谱分析的大多数情况。

3.布莱克曼窗：布莱克曼窗是一种设计用于音频处理的窗函数，它在时间域和频域上都具有较好的性能。

它的形状和汉明窗类似，但有更宽的底部。

布莱克曼窗的特点是具有更强的边瓣抑制能力，相对于汉明窗能够更好地抑制频谱波动和频谱泄露。

它适用于对频谱准确性要求较高的信号处理任务。

综上所述，不同的窗函数在频域上具有不同的特性。

矩形窗适用于频谱较窄的信号，提供较好的分辨率；汉明窗适用于大多数频谱分析的情况，具有较低的波动；布莱克曼窗能够更好地抑制频谱波动和泄露，适用于对准确性要求较高的任务。

在实际应用中，选择窗函数需要根据具体的信号特性和分析需求来进行。

需要折衷考虑分析的准确性和频谱泄露问题，并选择合适的窗函数来优化频谱分析的结果。

函数实验报告总结函数实验报告总结引言：函数是计算机编程中的重要概念，它能够将一组输入映射为输出，是程序设计中模块化和可重用性的基石。

为了更好地理解函数的概念和使用方法，我们进行了一系列的函数实验。

本文将对这些实验进行总结和归纳，探讨函数在实际编程中的应用。

实验一：函数的定义和调用在这个实验中，我们学习了函数的基本概念和语法。

通过定义一个简单的函数，我们了解了如何使用关键字“def”来定义函数，并通过调用函数来执行其中的代码块。

这个实验让我们明白了函数的封装性和可复用性，可以将一段代码封装成函数，供其他地方调用。

实验二：函数的参数传递在这个实验中，我们学习了函数的参数传递方式。

通过定义带有参数的函数，我们了解了函数参数的不同类型，包括位置参数、关键字参数和默认参数。

我们还学习了如何在函数调用时传递参数，并探讨了参数传递的机制和注意事项。

这个实验让我们对函数的灵活性和可变性有了更深入的理解。

实验三：函数的返回值在这个实验中，我们学习了函数的返回值。

通过定义带有返回值的函数，我们了解了如何使用关键字“return”来返回函数执行的结果。

我们还学习了函数返回值的类型和用途，包括返回单个值、返回多个值和返回空值。

这个实验让我们明白了函数的结果可以被其他代码使用，提高了代码的灵活性和可扩展性。

实验四：递归函数在这个实验中，我们学习了递归函数的概念和用法。

通过定义递归函数来解决问题，我们了解了递归的原理和应用场景。

我们还学习了递归函数的优缺点，包括代码简洁但可能导致性能问题。

这个实验让我们对递归思想和算法有了更深入的认识，提高了问题解决的能力。

实验五：高阶函数在这个实验中，我们学习了高阶函数的概念和用法。

通过定义接受函数作为参数或返回函数的函数，我们了解了高阶函数的特点和应用场景。

我们还学习了匿名函数和函数式编程的基本概念，以及如何使用内置函数和自定义函数来实现高级功能。

这个实验让我们对函数的扩展性和灵活性有了更深入的理解。

三角函数的实际应用三角函数是数学中重要的概念之一，它们不仅仅是理论上的概念，在日常生活中也有着广泛的实际应用。

三角函数的实际应用涉及到多个领域，包括物理、工程、天文学以及计算机图形等。

本文将介绍三角函数在这些领域中的一些实际应用案例，并探讨其重要性和影响。

一、物理应用1. 弹簧振动弹簧振动是物理学中常见的现象，它是由于弹性体受到外力作用而发生的周期性振动。

三角函数可以用来描述弹簧振动的运动规律。

根据胡克定律，弹簧振动的恢复力与其伸长长度成正比。

这个关系可以用正弦函数表示，即 F = k*sin(ωt)，其中 F 表示恢复力，k 表示弹性系数，ω 表示角频率，t 表示时间。

通过三角函数的表达，我们可以计算出弹簧振动的周期、频率等重要参数，进而研究和分析弹簧振动的性质，为相关实验和工程设计提供依据。

2. 交流电路在电学中，交流电路是一种重要的电路类型。

三角函数可以用来描述交流电路中电压和电流的变化情况。

正弦函数被广泛应用于交流电路的分析和计算中。

例如，正弦波电压在时间上的变化可以用 V(t) = Vm * sin(ωt) 表示，其中 V(t) 表示时间 t 时的电压值，Vm 表示电压的最大值，ω 表示角频率。

通过使用三角函数，我们可以计算交流电路中的功率、相位差等重要参数，从而更好地理解和设计电路。

二、工程应用1. 建筑设计在建筑设计中，三角函数被广泛地应用于计算和测量。

例如，三角函数可以用来计算建筑物的高度、倾斜度以及角度等信息。

在进行建筑物定位和测量时，使用三角函数可以通过测量某个点与两个已知点之间的距离和角度，推导出该点的准确位置和方向。

这对建筑师和工程师来说是非常重要的，它们可以基于这些计算结果进行建筑物的合理布局和设计。

2. 机械运动机械运动是工程学中的一个重要领域，三角函数在机械运动中具有广泛的应用。

例如，在机械设计中，三角函数可以描述旋转运动的速度和加速度，帮助工程师分析和计算各种机械零件的运动特性。

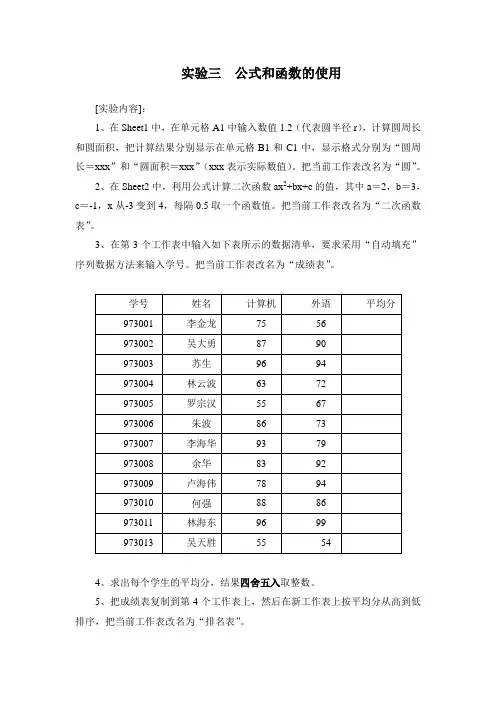
实验三公式和函数的使用[实验内容]：1、在Sheet1中，在单元格A1中输入数值1.2（代表圆半径r），计算圆周长和圆面积，把计算结果分别显示在单元格B1和C1中，显示格式分别为“圆周长＝xxx”和“圆面积＝xxx”（xxx表示实际数值）。

把当前工作表改名为“圆”。

2、在Sheet2中，利用公式计算二次函数ax2+bx+c的值，其中a＝2，b＝3，c＝-1，x从-3变到4，每隔0.5取一个函数值。

把当前工作表改名为“二次函数表”。

3、在第3个工作表中输入如下表所示的数据清单，要求采用“自动填充”序列数据方法来输入学号。

把当前工作表改名为“成绩表”。

4、求出每个学生的平均分，结果四舍五入取整数。

5、把成绩表复制到第4个工作表上，然后在新工作表上按平均分从高到低排序，把当前工作表改名为“排名表”。

6、把成绩表复制到第5个工作表上，然后在新工作表上通过RANK函数计算出每个学生平均分的名次，把当前工作表改名为“名次表”。

7、把“成绩表”复制到第6个工作表上，然后在新工作表上完成如下处理：1）、在“平均分”列的右边增加新列“总评”。

2）、根据以下条件，通过IF函数求出总评结果。

若平均分≥60，总评为“及格”；否则，总评为“不及格”。

3)、将当前工作表改名为“总评表”。

8、把“成绩表”复制到第7个工作表上，然后计算平均分各分数段人数（平均分≥90；平均分≥80；平均分≥70；平均分≥60；平均分<60。

）。

把结果存放在第6个工作表上。

再把平均分<60的单元格设置为加粗，红色字体。

将当前工作表改名为“各分数段表”。

9、逐一查看上述7个工作表。

10、保存并退出文件。

实验三窗函数特性分析窗函数特性分析是信号处理领域中一个重要的研究方向，通过对窗函数的分析可以有效地应用于噪声抑制、频谱分析等方面。

下面我们来详细分析几个常见的窗函数特性。

1.矩形窗矩形窗函数也被称为哈曼窗，其表达式为：w(n)={1(n∈[0,N-1])0otherwise(1)其中，N表示窗口长度。

矩形窗函数在频域上等效为一个 sinc 函数，其主瓣宽度与窗口长度成反比。

由于矩形窗函数在主瓣两侧具有较深的零点，因此具有较高的频率分辨率。

然而，由于其旁瓣较大，矩形窗函数容易产生假响应和泄露现象。

2.汉宁窗汉宁窗函数是一种改进的矩形窗函数，通过在矩形窗函数的基础上增加两个旁瓣，以减小旁瓣电平并抑制假响应。

汉宁窗函数的表达式为：w(n)=0.5−0.5cos⁡(2πnN−1)(2)其中，N表示窗口长度。

与矩形窗函数相比，汉宁窗函数的主瓣宽度增加了，旁瓣电平也较低。

在保持较高频率分辨率的同时，减小了假响应的可能性。

3.哈曼窗哈曼窗函数是一种基于最小旁瓣电平为目标的窗函数，通过调整汉宁窗函数的系数，使得旁瓣电平最小。

哈曼窗函数的表达式为：w(n)=0.4935N+0.4834cos⁡(2πnN−1)+0.0133cos⁡(4πnN−1)(3)其中，N表示窗口长度。

哈曼窗函数在主瓣两侧具有较深的零点，同时旁瓣电平较低，具有较高的频率分辨率和较小的假响应。

4.高斯窗高斯窗函数是一种基于高斯函数的窗函数，具有平滑的旁瓣衰减和较小的旁瓣电平。

高斯窗函数的表达式为：w(n)=e−n2/(2σ2)(4)其中，σ表示高斯函数的方差，N表示窗口长度。

高斯窗函数的主瓣宽度与窗口长度成反比，旁瓣电平随着远离主瓣而逐渐增大。

由于其旁瓣衰减较慢，高斯窗函数容易产生交叉干扰现象。

通过对以上常见窗函数的特性分析可知，不同的窗函数具有不同的频率响应特性。

在应用中需要根据具体需求选择合适的窗函数。

例如，当需要高频率分辨率时，可以选择矩形窗函数；当需要抑制假响应时，可以选择汉宁窗函数或哈曼窗函数；当需要平滑的旁瓣衰减时，可以选择高斯窗函数。

第一课时 三角函数的应用（一）任务一、整体感知问题 1 你能列举一些生活中具有周期性现象的例子吗？前面已经用三角函数模型刻画过哪些周期性现象？答案：生活中周期性现象的例子大致有三种类型：（1）匀速圆周运动．如水流量稳定条件下的筒车运动，钟表指针的转动，摩天轮的运动等；（2）物理学中的周期性现象．如弹簧振子运动，交变电流等；（3）生活中的周期性现象．如潮汐变化，一天当中的气温变化，四季变化，生物钟，波浪，音乐等．已经用三角函数模型刻画过匀速圆周运动．例如筒车运动、摩天轮的运动、钟表指针的转动等．任务二、新知探究1．问题研究1——简谐运动问题 2 观看弹簧振子的运动视频，振子运动过程中有哪些周期性现象？可以利用哪些变量之间的函数关系来刻画振子运动过程中的周期性现象？弹簧振子的运动（如图1）．答案：振子离开中心位置的位移随着时间呈周期性变化；振子所受的回复力随着时间呈周期性变化．所以可以用振子离开中心位置的位移s 与时间t 之间的函数关系，也可以用振子所受的回复力F 与时间t 之间的函数关系来刻画其运动过程中周期性现象．例1 某个弹簧振子在完成一次全振动的过程中，时间t （单位：s ）与位移y （单位：mm ）之间的对应数据如表1所示．试根据这些数据确定这个振子的位移关于时间的函数解析式．图12．建模解模问题3 例1中没有给出振子的位移关于时间的函数模型，根据以往的数学建模经验，我们应该按照什么样的流程完成这个建模过程？答案：搜集数据，画散点图——观察散点图并进行函数拟合，选择函数模型——利用数据信息，求解函数模型．活动：教师或者学生画出散点图．问题4观察画出的散点图，你认为可以用怎样的函数模型进行刻画位移y 随时间t 的变化规律？答案：根据散点图（如图2），分析得出可以用y =A sin(ωt +φ)这个函数模型进行刻画． 问题5 由数据表和散点图，你将如何求出函数的解析式？答案： 依据数据表和散点图，可得A =20，T =60s ，求得ω=3π10，然后将点（0，－20）的坐标代入解析式y =20sin(3π10t +φ)，解得φ=－2π+2k π，k ∈Z ，所以函数的解析式为y =20sin(3π10t －2π)，t ∈[0，+∞)． 教师补充：现实生活中存在大量类似弹簧振子的运动，如钟摆的摆动，水中浮标的上下浮动，琴弦的震动，等等．这些都是物体在某一中心位置附近循环往复的运动．在物理学中，把物体受到的力（总是指向平衡位置）正比于它离开平衡位置的距离的运动称为“简谐运动”．可以证明，在适当的坐标系下，简谐运动可以用函数y =A sin(ωx +φ)，x ∈[0，+∞)表示，其中A >0，ω>0．描述简谐运动的物理量，如振幅、周期和频率等都与这个解析式中的常数有关：图2表1A 就是这个简谐运动的振幅，它是作简谐运动的物体离开平衡位置的最大距离； 简谐运动的周期是2π=T ω，它是作简谐运动的物体往复运动一次所需要的时间； 简谐运动的频率是π21ω==T f ，它是作简谐运动的物体在单位时间内往复运动的次数； ωx +φ称为相位；x =0时的相位φ称为初相.问题6 例1中简谐运动的振幅、周期与频率各是多少？相位、初相分别是什么？答案：振幅A ＝20mm ，周期T ＝53s ，频率f ＝35次，相位为3π10t －2π，初相为－2π． 3．问题研究2——交变电流例2 如图3（1）所示的是某次实验测得的交变电流i （单位：A ）随时间t （单位：s ）变化的图象．将测得的图象放大，得到图3（2）．（1）求电流i 随时间t 变化的函数解析式；（2）当601,6007,1501,6001,0=t 时，求电流i ．4．建模解模问题7 观察图象，交变电流i 随时间t 的变化满足怎样的函数模型？其中每个参数的物理意义是什么？答案：由交变电流的产生原理可知，电流i 随时间t 的变化规律可以用i =A sin(ωt +φ)，t ∈[0，+∞)来刻画.其中A 为振幅，ωπ2为周期，ωt +φ为相位，φ为初相．问题8 根据图象3（2），你能说出电流的的最大值A ，周期T ，初始状态（t =0）的电流吗？由这些值，你能进一步完成例2的解答吗？答案：由图可知，A =5，T =501s ，初始状态的电流为4.33A ． 解：由图3（2）可知，电流最大为5A ，因此A =5；电流变化的周期T =501s ，即ωπ2=501s ，解得ω=100π；再由初始状态（t =0）的电流约为4.33A ，可得sin φ=0.866，因此φ约为3π．所图3（1） 图3（2）以电流i 随时间t 变化的函数解析式是 π5sin(100π)[0,)3i t t =+∈+∞，． 当0=t 时，235=i ； 当6001=t 时，5=i ； 当1501=t 时，0=i ； 当6007=t 时，5-=i ； 当601=t 时，0=i ． 练习1 如图4，一根绝对刚性且长度不变、质量可忽略不计的线，一端固定，另一端悬挂一个沙漏．让沙漏在偏离平衡位置一定角度（最大偏角）后在重力作用下铅锤面内做周期摆动．若线长l cm ，沙漏摆动时离开平衡位置的位移为s （单位：cm ）与时间t （单位：s ）的函数关系是).∞,0[∈),3cos(3++=t t l g s π （1）当l =25时，求沙漏的最大偏角（精确到0.0001rad ）；（2）已知g =9.8m/s 2，要使沙漏摆动的周期是1s ，线的长度应当是多少（精确到0.1cm ）?解：（1）∵)3cos(3π+=t l g s ，∴可得s 的最大值为3． 设偏角为θ，可得最大偏角满足sin θ=253．利用计算器计算可得θ=0.1203rad ． 答：当l =25时，沙漏的最大偏角为0.1203rad ．（2）沙漏摆动的周期为1π2==lgT ，解得2)π2(g l =，故cm 8.2)π2(8.92≈=l ． 图4答：要使沙漏摆动的周期是1s，线的长度l应当为24.8cm．任务三、归纳小结问题9 对于一个周期性现象，你该如何利用三角函数来刻画？在本节课中，涉及哪些数学思想？答案：利用三角函数刻画周期性现象，就是要找出这一现象中哪两个变量满足“当其中一个变量增加相同的常数时，另一个变量的值重复出现”，然后通过数学建模，求出这两个变量之间满足的三角函数关系．在本节课的学习中，涉及到数形结合思想和数学建模思想．。

《3.3 函数的应用（一）》作业设计方案（第一课时）一、作业目标本次作业旨在帮助学生进一步理解函数的概念和应用，掌握函数在解决实际问题中的方法，提高学生的数学应用能力和思维能力。

二、作业内容1. 案例分析：要求学生分析以下实际问题，并尝试使用函数来描述和解决：某地每月用电量X（单位：度）与电费Y（单位：元）的关系。

根据当地电价，请写出Y与X之间的函数关系式。

2. 数学实验：学生需要通过实验的方式，利用函数模型解决实际问题。

例如，可以让学生模拟股票价格的变化，通过函数模型预测未来的价格走势，或者模拟商品销售情况，通过函数模型预测销售量的变化。

3. 小组讨论：学生以小组为单位，讨论函数在日常生活中的应用，以及如何利用函数解决实际问题。

通过讨论，提高学生的数学应用意识和团队协作能力。

三、作业要求1. 独立完成：学生需独立完成作业，不得抄袭。

2. 准确描述：学生在分析实际问题时，需要准确描述函数关系式，并说明其实际意义。

3. 实验报告：学生需提交数学实验报告，包括实验目的、实验过程、实验结果及分析等。

4. 讨论发言：小组讨论环节，学生需要准备讨论发言稿，清晰表达自己的观点和看法。

四、作业评价1. 作业完成情况：根据学生提交的作业情况，评价学生是否认真完成作业，是否能够独立完成。

2. 案例分析能力：评价学生能否准确描述实际问题，并尝试使用函数来描述和解决。

3. 数学实验能力：根据学生提交的数学实验报告，评价学生是否能够正确使用函数模型解决实际问题，实验报告是否具有逻辑性和准确性。

4. 小组讨论表现：根据学生在小组讨论中的发言情况，评价学生的团队协作能力和表达能力。

五、作业反馈部分1. 学生自评：学生在提交作业的同时，需要对自己的作业进行评价，总结自己在完成作业过程中的收获和不足。

2. 教师评价：教师根据学生作业完成情况、案例分析能力、数学实验能力、小组讨论表现等方面进行评价，并给出反馈和指导建议。

3. 集体反馈：教师可组织班级同学进行互评，互相学习、取长补短，共同提高数学应用能力和思维能力。

在三角函数的应用问题课题研究中，我们首先要明白三角函数的基本概念和公式。

三角函数包括正弦函数、余弦函数、正切函数等，它们在数学和实际生活中有着广泛的应用。

在本文中，我将从简单到复杂的角度来探讨三角函数的应用问题，并深入研究其在各个领域中的具体应用。

1. 三角函数的基本概念三角函数是以角为自变量的函数，主要包括正弦函数、余弦函数和正切函数。

其中，正弦函数sinθ表示直角三角形中对边与斜边的比值，余弦函数cosθ表示直角三角形中邻边与斜边的比值，而正切函数tanθ表示直角三角形中对边与邻边的比值。

这些基本概念是研究三角函数应用问题的基础。

2. 三角函数在几何中的应用三角函数在几何中有着重要的应用，例如计算三角形的周长、面积和各个角的大小等。

通过三角函数的公式，我们可以准确地计算出三角形的各种属性，这对于建筑、土木工程等领域至关重要。

3. 三角函数在物理中的应用在物理学中，三角函数也有着重要的应用。

通过正弦函数可以描述声波的传播规律，通过余弦函数可以描述振动的规律，而正切函数则可以描述力的合成和分解规律。

三角函数在物理学中的应用不仅可以帮助我们更好地理解自然现象，还可以指导实际应用中的问题求解。

4. 三角函数在工程中的应用工程领域也是三角函数应用的重要领域之一。

在建筑设计中，我们常常需要借助正弦函数来计算房屋的倾斜角度；在航空航天工程中，我们需要利用余弦函数来计算飞行器的航迹角度；在通信工程中，正切函数的应用也是不可或缺的。

三角函数在工程中的应用问题需要我们深入思考和研究，以便更好地解决实际问题。

5. 三角函数在生活中的应用除了数学、物理、工程等领域，三角函数在日常生活中也有着广泛的应用。

在导航中，我们需要利用正弦函数来计算地理位置的坐标；在摄影中，我们需要借助余弦函数来调整镜头的角度；在音乐中，正切函数也被用来调节音调和频率。

三角函数在生活中的应用问题虽然看似简单，却涵盖了丰富的知识和技能。

总结与展望：通过对三角函数的应用问题进行深入研究，我们不仅可以提高数学水平，还可以拓展科学视野，更好地理解和应用理论知识。