人教版高中数学-基本不等式
- 格式:docx
- 大小:33.39 KB
- 文档页数:3

人教A版高中数学必修5《基本不等式》精品教案课题: 基本不等式:2ba ab +≤(第一课时)教材:人教版高中课程标准实验教科书《数学·必修5》第三章第四节 1 教材分析本节书介绍了两个不等式定理:(1)、如果R b R a ∈∈,,那么ab b a 222≥+①;(2)、如果0,0>>b a ,那么2ba ab +≤②。
这两个定理是解决一些数学问题和实际应用问题的重要的数学方法。
本节书教学共需3课时,这是第一课时,主要是了解探索基本不等式的证明过程,熟悉基本不等式的结构,为下节基本不等式的应用做准备(以下用①②代替两个定理)。
2 学生分析有了前面“不等式性质”的学习,学生要理解这两个定理难度并不大。
针对学生求知欲旺盛的特点,在教学中,以思考、探索、讨论为主要方法,适当加以讲解,使学生自己收获结论、总结方法,动手解决实际问题,并且增强学习数学的的信心。
3 教学策略(1)、以“孔融选蛋糕”为例引入,课件辅助,引导学生探究①的证明,并总结证明方法;利用正方形和弦图让学生了解①的几何意义,同时介绍“国际数学家大会”,培养学生的民族自豪感和使命感。
(2)、利用①式,通过“换元法”练习引入定理②,引导学生从不同角度探究②的证明过程,利用“半径和半弦的关系”让学生了解②的几何意义,并强调①②的联系与区别。
(3)、巩固练习。
设置三道习题由浅到深让学生对基本不等式逐渐熟悉,应用它们去比较大小、解决生活常见问题,最后让学生通过替换定理中的字母发现更多②式有趣的变形式,为下一节课铺垫。
4 教学目标(1)、知识目标了解不等式①②的证明过程和方法;了解不等式①②的几何意义;初步应用基本不等式比较大小,熟悉其变形式。
(2)、能力目标通过探究结果的汇报以及讨论活动,提高学生语言表达能力;在对不等式①②的证明过程中培养学生发现、比较、论证、转化等分析问题和解决问题的能力;通过掌握不等式①②的结构特点和运用不等式①②的适当变形,培养学生的思维能力和创新精神。


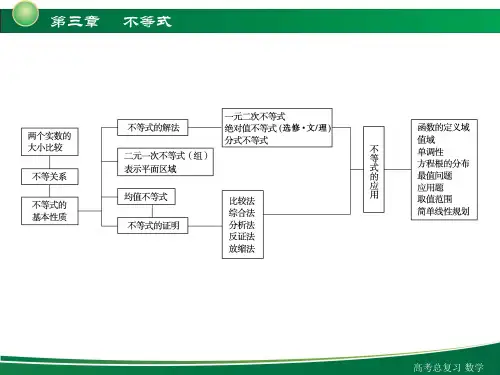






第四节 基本不等式【知识清单】1、如果R b a ∈,,那么ab b a 222≥+(当且仅当b a =时,等号成立) 2、基本不等式: 如果0,>b a ,那么ab ba ≥+2(当且仅当b a =时,等号成立) (其中2ba +称为算术平均数,ab 称为几何平均数,因此也称均值不等式) 注:两个正数的算术平均数不小于其几何平均数。
3、利用基本不等式求最值问题 已知,0,0>>y x 则(1)若积xy 是定值,p 则当且仅当y x =时,y x +有最小值是.2p (记:积定和最小).(2)若和y x +是定值,p ,则当且仅当y x =时,xy 有最大值是.42p (记:和定积最大). 注①基本不等式主要是利用和积转化求最值。
②利用基本不等式求最值时,要注意其必须满足的三个条件:01一正二定三相等.“一正”就是各项必须为正数;【例】 )0(41>+=x xx y 的最小值是________ 解析:141241=⋅≥+=x x x x y (当且仅当x x 41=即21=x 时,等号成立) 【例】若正数b a ,满足111=+b a ,则11614-+-b a 的最小值________ 解析:111=+b a 变形为ab b a =+;161642)1)(1(64211614=+--=--≥-+-b a ab b a b a 02“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值; 【例】已知45<x ,则函数54124-+-=x x y 的最小值为______ 解析:,2)]54([1)]54([≥--+--x x (当且仅当41=x 时,等号成立)1541242)54(1)54(≤-+-⇒-≤-+-x x x x03“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.这是只能利用对勾函数结合单调性或导数解决。
数学人教B 选修4-5第一章1.2 基本不等式1.了解两个或三个正数的算术平均值和几何平均值. 2.理解定理1和定理2(基本不等式).3.探索并了解三个正数的算术—几何平均值不等式的证明过程. 4.掌握用基本不等式求一些函数的最值及实际的应用问题.1.定理1设a ,b ∈__,则a 2+b 2≥2ab ,当且仅当____时,等号成立.【做一做1】已知θ∈⎣⎡⎦⎤0,π2,则sin θcos θ的最大值为__________. 2.定理2(基本不等式或平均值不等式)(1)如果a ,b 为____,则a +b2≥ab ,当且仅当____时,等号成立.(2)称______为正数a ,b 的算术平均值,____为正数a ,b 的几何平均值.(3)基本不等式可用语言叙述为:两个正数的________大于或等于它们的__________.(1)a 2+b 2≥2ab 与a +b2≥ab 成立的条件是不同的:前者只要求a ,b 都是实数,而后者要求a ,b 都是正数.有些同学易忽略这一点,例如:(-1)2+(-4)2≥2×(-1)×(-4)成立,而(-1)+(-4)2≥(-1)×(-4)不成立.(2)a 2+b 2≥2ab 与a +b2≥ab 都是带有等号的不等式.“当且仅当a =b 时,等号成立”这句话的含义是“a =b ”是“=”成立的充要条件,这一点至关重要,忽略它,往往会导致解题错误.(3)由公式a 2+b 2≥2ab 和a +b 2≥ab 可得到结论:①a b +b a ≥2(a ,b 同号);②21a +1b ≤ab≤a +b 2≤a 2+b 22(a ,b 是正数).(4)定理中的a ,b 可以是数字,也可以是比较复杂的代数式. 【做一做2-1】下列不等式中正确的是( )A .若a ,b ∈R ,则b a +a b ≥2b a ·ab=2B .若x ,y 都是正数,则lg x +lg y ≥2lg x ·lg yC .若x <0,则x +4x ≥-2x ·4x =-4D .若x ≤0,则2x +2-x ≥22x ·2-x =2【做一做2-2】若log 2x +log 2y =4,则x +y 的最小值是__________. 3.定理3(三个正数的算术—几何平均值不等式或平均值不等式)(1)如果a ,b ,c 为正数,则a +b +c3≥____,当且仅当________时,等号成立.(2)称________为正数a ,b ,c 的算术平均值,______为正数a ,b ,c 的几何平均值. (3)定理3可用语言叙述为三个正数的____________不小于它们的________. 【做一做3】已知x ,y ,z 是正数,且x +y +z =6,则lg x +lg y +lg z 的取值范围是( ) A .(-∞,lg 6] B .(-∞,3lg 2] C .[lg 6,+∞) D .[3lg 2,+∞)4.定理4(一般形式的算术—几何平均值不等式)如果a 1,a 2,a 3,…,a n 为n 个正数,则a 1+a 2+…+a n n≥na 1a 2…a n ,并且当且仅当__________时,等号成立.【做一做4】若a ,b ,c ,d 是正数,则b a +c b +d c +ad的最小值为__________.答案:1.R a =b【做一做1】12 由a ,b ∈R ,a 2+b 2≥2ab ,得ab ≤a 2+b 22,∴sin θcos θ≤sin 2θ+cos 2θ2=12.当且仅当sin θ=cos θ,即θ=π4时等号成立.2.(1)正数 a =b (2)a +b2ab (3)算术平均值 几何平均值【做一做2-1】D 对于选项A ,当a ·b >0时,b a +ab≥2;对于选项B ,当x >1,y >1时,有lg x +lg y ≥2lg x ·lg y ;对于选项C ,当x <0时,x +4x=-⎝⎛⎭⎫-x -4x ≤-24=-4. 【做一做2-2】4 由题意可知x >0,y >0,log 2xy =4, ∴xy =4.∴x +y ≥2xy =4,当且仅当x =y =2时,等号成立. 故x +y 的最小值为4.3.(1)3abc a =b =c (2)a +b +c 33abc (3)算术平均值 几何平均值【做一做3】B ∵x ,y ,z 是正数,∴xyz ≤⎝⎛⎭⎫x +y +z 33=23.∴lg x +lg y +lg z =lg xyz ≤lg 23=3lg 2,当且仅当x =y =z =2时,等号成立. 4.a 1=a 2=…=a n 【做一做4】4 由定理4可得,b a +c b +d c +ad ≥44b a ·c b ·d c ·a d=4,当且仅当a =b =c =d时,等号成立.1.三个或三个以上正数的平均值不等式的应用条件是什么?剖析:“一正”:不论是三个数的平均值不等式或者n 个数的平均值不等式,都要求是正数,否则不等式是不成立的.如a +b +c ≥33abc .取a =b =-2,c =2时,a +b +c =-2,而33abc =6,显然-2≥6不成立.“二定”:包含两类求最值问题:一是已知n 个正数的和为定值(即a 1+a 2+…+a n 为定值),求其积a 1a 2…a n 的最大值;二是已知乘积a 1a 2…a n 为定值,求其和a 1+a 2+…+a n 的最小值.“三相等”:取“=”号的条件是a 1=a 2=a 3=…=a n ,不能只是其中一部分值相等. 2.如何使用基本不等式中的变形与拼凑方法?剖析:为了使用基本不等式求最值(或范围等),往往需要对数学代数式变形或拼凑数学结构,有时一个数拆成两个或两个以上的数,这时候,拆成的数要相等,如y =4x 4+x 2=4x4+x 22+x 22,其中把x 2拆成x 22+x 22,这样可满足不等式成立的条件,若变形为y =4x 4+x 2=4x 4+x 24+34x 2,虽然满足了乘积是定值这个要求,但“三相等”这个要求就无法满足了,这是因为取“=”号的条件是4x 4=x 24=34x 2,显然x 无解.题型一 利用基本不等式比较大小【例题1】设a ,b ∈(0,+∞),试比较a +b 2,ab ,a 2+b 22,2aba +b的大小,并说明理由.分析:解答本题应充分利用基本不等式及其变形,不等式的性质.反思:基本不等式有着重要的应用,在使用时还应记住重要的变形公式.如a ,b 是正数,且b ≥a 时,a ≤2ab a +b ≤ab ≤a +b 2≤a 2+b 22≤b ,其中2ab a +b =21a +1b 为a ,b 的调和平均值,ab 为a ,b 的几何平均值,a +b 2为a ,b 的算术平均值,a 2+b 22为a ,b 的平方平均值.要注意公式的推导和结论的运用:调和平均值≤几何平均值≤算术平均值≤平方平均值.题型二 利用基本不等式求最值【例题2】(1)已知x ,y 是正数,且x +2y =1,求1x +1y的最小值;(2)已知x >0,y >0,且5x +7y =20,求xy 的最大值;(3)已知x <54,求y =4x -1+14x -5的最大值;(4)已知a >0,b >0,且a 2+b 22=1,求a 1+b 2的最大值; (5)已知x 是正数,求函数y =x (1-x 2)的最大值; (6)θ为锐角,求y =sin θ·cos 2θ的最值.分析:根据题设条件,合理变形,创造能用基本不等式的条件.反思:解题时要注意考察“三要素”:(1)函数中的相关项必须都是正数;(2)变形后各项的和或积有一个必须是常数;(3)当且仅当各项相等时,才能取到等号,可简化为“一正二定三相等”.求函数的最值时,常将不满足上述条件的函数式进行“拆”、“配”等变形,使其满足条件,进而求出最值.题型三 基本不等式的实际应用【例题3】某国际化妆品生产企业为了占有更多的市场份额,拟在2012年英国伦敦奥运会期间进行一系列促销活动,经过市场调查和测算,化妆品的年销量x 万件与年促销费t 万元之间满足3-x 与t +1成反比例的关系,如果不搞促销活动,化妆品的年销量只能是1万件,已知2012年生产化妆品的设备折旧、维修等固定费用为3万元,每生产1万件化妆品需要投入32万元的生产费用,若将每件化妆品的售价定为其生产成本的150%与平均每件促销费的一半之和,则当年生产的化妆品正好能销完.(1)将2012年的利润y (万元)表示为促销费t (万元)的函数;(2)该企业2012年的促销费投入多少万元时,企业的年利润最大?分析:表示出题中的所有已知量和未知量,利用它们之间的关系列出函数表达式,再应用不等式求最值.反思:解答不等式的实际应用问题,一般可分为如下四步:①阅读理解材料:应用题所用语言多为“文字语言、符号语言、图形语言”并用,而且多数应用题篇幅较长.阅读理解材料要达到的目的是将实际问题抽象成数学模型.这就要求解题者领悟问题的实际背景,确定问题中量与量之间的关系,初步形成用怎样的模型能够解决问题的思路,明确解题方向.②建立数学模型:根据①中的分析,把实际问题用“符号语言”、“图形语言”抽象成数学模型,并且建立所得数学模型和已知数学模型的对应关系,以便确立下一步的努力方向.③讨论不等关系:根据题目要求和②中建立起来的数学模型,讨论与结论有关的不等关系,得出有关理论参数的值.④得出问题结论:根据③中得到的理论参数的值,结合题目要求得出问题的结论. 题型四 易错辨析易错点:利用基本不等式求最值时,应注意不等式成立的条件,即变量为正实数,和或积为定值,等号成立,三者缺一不可.【例题4】求函数y =1-2x -3x 的值域.错解:∵y =1-2x -3x =1-⎝⎛⎭⎫2x +3x ,而2x +3x ≥22x ×3x =26,当且仅当2x =3x,即x =±62时,等号成立,故值域为(-∞,1-26].错因分析:在应用基本不等式时未保证2x ,3x为正值这一条件成立.答案:【例题1】解:∵a ,b ∈(0,+∞),∴ab ≤a +b2(当且仅当a =b 时取等号),1a +1b ≥2ab, ∴ab ≥21a +1b=2aba +b (当且仅当a =b 时取等号).又⎝⎛⎭⎫a +b 22=a 2+b 2+2ab 4≤a 2+b 2+a 2+b 24=a 2+b 22.∴a +b 2≤a 2+b 22(当且仅当a =b 时取等号).综上,2aba +b≤ab ≤a +b 2≤a 2+b 22(当且仅当a =b 时取等号).【例题2】解:(1)因为x +2y =1,所以1x +1y =x +2y x +x +2y y =3+2y x +x y≥3+22y x ·xy =3+22,当且仅当2y x =xy,x +2y =1,即x =2-1,y =1-22时,等号成立.所以当x =2-1,y =1-22时,1x +1y取最小值3+2 2.(2)xy =135(5x ·7y )≤135⎝⎛⎭⎫5x +7y 22=135×⎝⎛⎭⎫2022=207, 当且仅当5x =7y =10,即x =2,y =107时,等号成立,此时xy 取最大值207.(3)因为x <54,所以4x -5<0,故5-4x >0.所以y =4x -1+14x -5=-⎝⎛⎭⎫5-4x +15-4x +4.因为5-4x +15-4x ≥2(5-4x )·15-4x=2,所以y ≤-2+4=2.当且仅当5-4x =15-4x,即x =1时,等号成立.所以当x =1时,y 取最大值2.(4)a 1+b 2=a 2⎝⎛⎭⎫12+b 22=2a ·12+b 22≤22⎣⎡⎦⎤a 2+⎝⎛⎭⎫12+b 22=324, 当且仅当a =12+b 22,即a =32,b =22时,等号成立,此时a 1+b 2有最大值324.(5)∵y =x (1-x 2),∴y 2=x 2(1-x 2)2=2x 2(1-x 2)(1-x 2)·12.∵2x 2+(1-x 2)+(1-x 2)=2,∴y 2≤12⎝⎛⎭⎫2x 2+1-x 2+1-x 233=427.当且仅当2x 2=1-x 2,即x =33时,等号成立.∴y ≤239,即y max =239.(6)y 2=sin 2θcos 2θcos 2θ =12·2sin 2θ(1-sin 2θ)(1-sin 2θ) ≤12⎝⎛⎭⎫233=427, 当且仅当2sin 2θ=1-sin 2θ,即sin θ=33时,等号成立.∴y max =239.【例题3】解:(1)由题意可设 3-x =kt +1(k ≠0).将t =0,x =1代入,得k =2.∴x =3-2t +1.当年生产x 万件时,∵年生产成本=年生产费用+固定费用,∴年生产成本为32x +3=32⎝⎛⎭⎫3-2t +1+3.当销售x 万件时,年销售收入为150%⎣⎡⎦⎤32⎝⎛⎭⎫3-2t +1+3+12t .由题意,生产x 万件化妆品正好销完,由年利润=年销售收入-年生产成本-促销费,得年利润y =-t 2+98t +352(t +1)(t ≥0).(2)y =-t 2+98t +352(t +1)=50-⎝⎛⎭⎪⎫t +12+32t +1 ≤50-2t +12×32t +1=50-216=42, 当且仅当t +12=32t +1,即t =7时,等号成立,此时y max =42,∴当促销费投入为7万元时,企业的年利润最大.【例题4】正解:当x >0时,y =1-2x -3x=1-⎝⎛⎭⎫2x +3x ≤1-26,当且仅当2x =3x ,即x =62时,等号成立.当x <0时,y =1+⎣⎡⎦⎤(-2x )+⎝⎛⎭⎫-3x ≥1+2(-2x )·⎝⎛⎭⎫-3x =1+26, 当且仅当-2x =-3x ,即x =-62时,等号成立.∴所求函数的值域为(-∞,1-26]∪[1+26,+∞).1下列函数中,最小值为2的是( )A .y =x 2+2xB .y =x 2+2+1x 2+2C .y =sin x +sec x ,x ∈⎣⎡⎦⎤0,π2 D .y =7x+7-x2(2012·山东青岛一模)已知a >0,b >0,且2a +b =4,则1ab的最小值为( )A .14B .4C .12D .23若a >b >0,则a +1b (a -b )的最小值是( )A .3B .4C .5D .64周长为l 的矩形的面积的最大值为__________,对角线长的最小值为__________.5若a ,b ∈(0,+∞),且a +b =1,则a 2+b 2的最小值为__________,1a 2+1b2的最小值为__________.答案:1.D 对于选项A ,需考虑x 的符号;对于选项B ,不能用基本不等式求最值,等号不成立;对于选项C ,x =π2时sec x 无意义.对于选项D ,y =7x +7-x ≥27x ·7-x =2,当且仅当7x=7-x ,即x =0时,等号成立.2.C3.A ∵a >b >0,∴a +1b (a -b )=(a -b )+b +1b (a -b )≥33(a -b )·b ×1b (a -b )=3,当且仅当a -b =b =1b (a -b ),即a =2,b =1时等号成立.4.l 216 24l 设矩形的两邻边长分别为x ,y ,则x +y =l 2,∴面积S =xy ≤⎝⎛⎭⎫x +y 22=l 216(当且仅当x =y 时取等号),对角线长a =x 2+y 2≥(x +y )22=24l (当且仅当x =y 时取等号).5.12 8 因为a >0,b >0,则a 2+b 2≥(a +b )22=12,当且仅当a =b =12时取等号, 1a 2+1b 2=a 2+b 2a 2b 2≥2ab ≥2⎝⎛⎭⎫a +b 22=8,当且仅当a =b =12时取等号.1设x ,y ∈(0,+∞),且满足x +4y =40,则lg x +lg y 的最大值是( ) A .40 B .10 C .4 D .2答案:D ∵x ,y ∈(0,+∞),42x y+≤.44x y+=10,∴xy ≤100. ∴lg x +lg y =lg xy ≤lg 100=2.当且仅当x =4y ,即x =20,y =5时等号成立.2若a >b >1,P 1(lg lg )2Q a b =+,lg 2a b R +⎛⎫⎪⎝⎭=,则( )A .R <P <QB .P <Q <RC .Q <P <RD .P <R <Q答案:B ∵a >b >1,∴lg a >lg b >0且2a b+>∴Q =1(lg lg 2a b -P .R =lg 2a b +⎛⎫⎪⎝⎭1(lg lg )2a b +=Q , ∴R >Q >P .3若x >0,则294x x+的最小值是( )A .9B .C .13D .不存在答案:B 因为x >0,所以294x x +=2922x x x ++≥,当且仅当292=x x ,即x 时等号成立. 4已知不等式1()9a x y x y ⎛⎫+≥⎪⎝⎭+对任意正实数x ,y 恒成立,则正实数a 的最小值为( )A .2B .4C .6D .8答案:B 1()a x y x y ⎛⎫++⎪⎝⎭=1+ax ya y x ++≥1+a +=2(当且仅当yx=). ∵1()a x y x y ⎛⎫++ ⎪⎝⎭≥9对任意正实数x ,y 恒成立,∴2≥9.∴a ≥4.5若正数a ,b 满足ab =a +b +3,则ab 的取值范围是______.答案:[9,+∞) t (t >0),由ab =a +b +3≥3, 则有t 2≥2t +3,即t 2-2t -3≥0.解得t ≥3或t ≤-1(不合题意,舍去).3.∴ab ≥9,当且仅当a =b =3时取等号.6若正实数x ,y ,z 满足x -2y +3z =0,则2y xz的最小值是______.答案:3 由x -2y +3z =0,得y =32x z +,代入2y xz,得229666=344x z xz xz xzxz xz +++≥,当且仅当x =y =3z 时取“=”.7若直线2ax -by +2=0(a >0,b >0)经过圆x 2+y 2+2x -4y +1=0的圆心,则11a b+的最小值是__________.答案:4 圆x 2+y 2+2x -4y +1=0,即(x +1)2+(y -2)2=4,其圆心为(-1,2). 又直线2ax -by +2=0(a >0,b >0)过圆心(-1,2), 所以-2a -2b +2=0,化简得:a +b =1(a >0,b >0).所以111a b a b ab ab++==. 又2124a b ab +⎛⎫≤= ⎪⎝⎭,所以1114a b ab +=≥,当且仅当a =b =12时等号成立. 8(2012·江苏徐州第一次质检)已知a 1,a 2,…,a n 都是正数,且a 1·a 2·…·a n =1,求证:(2+a 1)(2+a 2)…(2+a n )≥3n.答案:证明:因为a 1是正数,所以2+a 1=1+1+a 1≥同理2+a j =1+1+a j ≥j =2,3,…,n ),将上述不等式两边相乘,得(2+a 1)(2+a 2)…(2+a n )≥3n 因为a 1·a 2·…·a n =1,所以(2+a 1)(2+a 2)…(2+a n )≥3n .当且仅当a 1=a 2=…=a n =1时,等号成立.9如图所示,将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ,要求B 在AM 上,D 在AN 上,且对角线MN 过C 点,已知AB =3米,AD =2米.(1)要使矩形AMPN 的面积大于32平方米,则AN 的长应在什么范围内? (2)当AN 的长度是多少时,矩形AMPN 的面积最小?并求最小面积. 答案:解:(1)设AN =x (x >2),则ND =x -2.由题意,得ND AN DC AM =,∴23x x AM-=.∴3=2xAM x -.∴S 矩形AMPN =32xx x ⋅->32. ∴3x 2-32x +64>0.∴(3x -8)(x -8)>0. ∴2<x <83或x >8. ∴AN 的长的范围是82,3⎛⎫⎪⎝⎭∪(8,+∞).(2)S 矩形AMPN =2233(2)12(2)1222x x x x x -+-+=-- =123(2)++122x x --≥, 当且仅当x =4时取“=”.∴当AN 的长度为4米时,矩形AMPN 的面积最小,矩形AMPN 的最小面积为24平方米.10求函数y =a <b )的最大值. 答案:解:解法一:函数的定义域为[a ,b ],y >0, 所以y 2=b a -+2(b -a ),当且仅当=2a bx -时,等号成立. 所以y解法二:利用不等式22222a b a b ++⎛⎫≥ ⎪⎝⎭.22=22y ⎛⎛⎫ ⎪ ⎝⎭⎝⎭()()22x a b x b a-+--≤=, 所以y 2≤2(b -a ),即y ≤当且仅当x -a =b -x ,即2b ax +=时,等号成立,所以max y。
《不等式的性质》教学设计
一. 教学内容解析;
本节课是《普通高中课程标准实验教科书·数学必修5)》(人教A 版)第三章第一节的第二课《不等式的性质》。
这节的主要内容是不等式的概念、不等式与实数运算的关系和不等式的性质.这部分内容是不等式变形、化简、证明的理论依据及基础.教材通过具体实例,让学生感受现实生活中存在大量的不等关系.在不等式与实数运算的关系基础上,系统归纳和论证了不等式的一系列性质.教学重点是比较两个实数大小的方法和不等式的性质。
二.教学目标设置;
1.通过具体情境,让学生感受现实世界和日常生活中存在着大量的不等关系,理解不等关系与不等式的联系,会用不等式表示不等关系.
2.理解并掌握比较两个实数大小的方法.
3.引导学生归纳和总结不等式的性质,并利用比较实数大小的方法论证这些性质,培养学生的合情推理和逻辑论证能力.
三.学生学情分析;
在初中的学习中,学生已将掌握了不等式关于加减和乘除的性质,本节课所需要解决的问题是(1)利用公理化的体系构建学生对于所学不等式性质的认识,让学生更好的从本质上体会不等式的性质,(2)学习关于不等式原来不完善的地方,比如对称性和传递性,还要学习两个不等式间的加减乘除次方开方运算。
教学难点是让学生体会公理化体系下不等式性质的证明及其应用.
四.教学策略分析;
这节内容从实际问题引入不等关系,进而用不等式来表示不等关系,自然引出不等式的基本性质.通过求解方程和求解不等式相对照,梳理初中已学习的等式性质、不等式性质,探索等式、不等式的共性,归纳出等式性质、不等式性质的研究思路和思想方法,猜想不等式的基本性质,并给出证明。
让学生体会“运算”在研究不等式性质中的关键作用。
为了研究不等式的性质,首先学习比较两实数大小的方法,这是论证不等式性质的基本出发点,故必须让学生明确.在教师的引导下学生基本上可以归纳总结出不等式的一系列性质,但对于这些性质的证明有些学生认为没有必要或对论证过程感到困惑,为此,必须明确论证性质的方法和要点,同时引导学生认识到数学中的定理、法则等,要通过公理化的论证才予以认可,培养学生的数学理性精神.
五.教学过程设计;
引入:
1.古诗横看成岭侧成峰,远近高低各不同,引出不等关系。
2.求解方程213132
x x +-=和不等式213132x x +->梳理初中已学习的等式性质、不等式性质,探索等式、不等式的共性,归纳出等式性质、不等式性质的研究思路和思想方法,
讲解新课:
1.通过实例,2,3比较大小,22,2a a +比较大小引出判断两个实数大小的充要条件是:
2.利用判断大小的运算方法证明不等式的性质:
性质3:如果a>b ,那么a+c>b+c .即a>b a+c>b+c
证明:∵a>b , ∴a-b>0,
∴(a+c)-( b+c)>0 即a+c>b+c
性质4 如果a>b,且c>0,那么ac>bc;
如果a>b,且c<0,那么ac<bc.
在解不等式的过程中4554x x ->⇒<-,可以吗?可以证明吗?
性质1:如果a>b ,那么b<a ,如果b<a ,那么a>b .(对称性)
即:a>b b<a ;b<a a>b
证明:∵a>b ∴a-b>0
由正数的相反数是负数,得-(a-b)<0
即b-a<0 ∴b<a .
两个事物不容易比大小的时候,我们经常寻找中间量,这体现了怎样的数学思想呢? 性质2:如果a>b ,且b>c ,那么a>c .(传递性)
即a>b ,b>c a>c
证明:∵a>b ,b>c ∴a-b>0, b-c>0
根据两个正数的和仍是正数,得
(a-b)+( b-c)>0 即a -c>0
∴a>c
性质5:如果a>b ,且c>d ,那么a+c>b+d .(相加法则)
即a>b , c>d a+c>b+d .
证法一: a+c>b+d
证法二:
a+c>b+d 例 已知a>b ,c<d ,求证:a-c>b-d .(相减法则)
分析:思路一:证明“a -c >b -d ”,实际是根据已知条件比较a -c 与b -d 的大小,所以以实数的运算性质与大小顺序之间的关系为依据,直接运用实数运算的符号法则来确定差的符号,最后达到证题目的
证法一:∵a >b ,c <d
∵a -b >0,d -c >0
∴(a -c )-(b -d )
=(a -b )+(d -c )>0(两个正数的和仍为正数)
>-⇔>b a b a 0=-⇔=b a b a 0<-⇔<b a b a ⇒⇒⇒⇒⇒⇒⎭⎬⎫+>+⇒>+>+⇒>d b c b d c c b c a b a ⇒>-+-⇒⎭
⎬⎫>-⇒>>-⇒>000d c b a d c d c b a b a
故a -c >b -d
思路二:我们已熟悉不等式的性质中的定理1~定理3及推论,所以运用不等式的性质,加以变形,最后达到证明目的
证法二:∵c <d ∴-c >-d
又∵a >b
∴a +(-c )>b +(-d )
∴a -c >b -d
对于两个不等式的运算我们知道有加法减法,那么有没有乘法呢?我们一起研究一下 性质6:相乘法则 a>b >0,且c>d>0⇒ac>bd
性质7:如果a>b>0,那么an >bn (n∈N ,且n>0)
性质8: 如果a>b>0,那么(n∈N ,且n>1).
小结 :本节课我们学习了不等式的性质,理解不等式性质的反对称性(a >b b <a =、传递性(a >b ,b >c a >c )、可加性(a >b a +c >b +c )、加法法则(a >b ,c >d a +c >b +d ),并记住这些性质的条件,尤其是字母的符号及不等式的方向,要搞清楚这些性质的主要用途及其证明的基本方法
六.课堂教学目标检测
1.下列说法正确的是________.
①若a >b ,则ac 2>bc 2;
②若a >b ,则1a <1b
; ③若ac 2>bc 2,则a >b ;
④若a <b <0,则a 2>ab >b 2;
⑤若c >a >b >0,则a c -a >b c -b
; ⑥若a >b 且1a >1b
,则a >0,b <0;⑧若a >b ,则lg a >lg b . 2.已知-6<a <8,2<b <3,分别求2a +b ,a -b ,a b
的取值范围.
⇔⇒⇒⇒。