导数的几何意义说课课件【说课比赛精华版】
- 格式：ppt
- 大小：399.50 KB
- 文档页数：26
文档推荐
-
导数的几何意义说课PPT课件页数:25
-
导数的几何意义教案word页数:14
-
导数的几何意义说课课件【说课比赛精华版】页数:26
-
导数的几何意义-教案(详案)页数:9
-
高中数学《导数的几何意义》的说课稿页数:4
下载文档原格式
合集下载
导数的几何意义课件
6
（2）求曲线y=f(x)=x2+1在点P(1,2)处的切
线方程.
y |x1
lim [(1
x0
x)2
1] (12 x
1)
lim
x0
2x x2 x
2
y 2 2(x 1)
2x y 0
例2.在函数 h(t) 4.9t 2 6.5t 10 的
回 顾
(2)求平均变化率 y f (x 0 x) f (x0 ) ;
x
x
(3)取极限，得导数f
( x0
)
lim
x0
y x
.
你能借助函数 f (x)的图象说说平均变化率
f x0 x f (x0 )表示什么吗？请在函数
x 图象中画出来．
平均变化率表示的是割线 PPn 的斜率
t0 附近比较平坦，几乎没有升降．
h / (t1 ), h / (t2 ) 0
曲线在
t1 ,
t3 ,
t2
t4
处切线 l1 ,
l3 ,
l2
l4
的斜率 小于0 大于
h/ (t3 ), h/ (t4 ) 0
在 t1 , t2 附近，曲线下降 ，函数在 t1 , t2
t3, t4
附近单调 递减
上升
t3, t4
圆的切线
割线斜率
在 x 0的过程中，割线PPn的的变化情况 你能描述一下吗？ 请在函数图象中画出来．
曲线的切线定义
当点 Pn (x0 x , f (x0 x)) 沿着曲线 f (x) 逼近点 P(x0 , f (x0 )) 时，即x 0，割线 PPn 趋近于确定的位置，这个确定位置上
《3.1.3导数的几何意义》说课课件
h
l0
0 t3 t4 t0
t1 t2 l2
t l1
东莞市樟木头中学 李鸿艳
教材 说明 分析 反思
教学 目标
板书 设计
教学过程 设计意图
重点与 难点 教学方法 与手段
教材分析
导数是微积分的核心概念之一，它为研究变量 和函数提供了重要的方法。《导数的几何意义》从 形的角度即割线入手，定义了切线，获得了导数的 几何意义。通过学习，可以帮助学生更好的理解导 数的概念及导数是研究函数的单调性、极值等性质 最有效的工具。与旧教材相比，新教材用形象直观 的“逼近”方法得到导数的几何意义，更有利于学 生对知识的理解和掌握。
▲问(一)：平面几何中我们怎样
判断直线是否是圆切线(图1)? ▲问(二)：如图直线l1是曲线C的 切线吗? l2能叫做过点P的曲2 l1
y=f(x)
o
x
图2
固旧引新， 为引入“导 数的几何意 义”奠定基 础.
▲问(三)求导数f′(x0)的步 骤有哪几步? ▲问(四)：平均变化率
教法 分析
(1)本节课采用的教法有：多媒体教学法、探究 发现法、分组讨论法。理论依据：利用多媒体 展示导数就是切线斜率的过程，让学生体会逼 近的思想方法，使问题变得直观，易于突破难 点。通过“动手探索、讨论验证、实践应用”， 让学生体验动手乐趣，增强参与意识，使他们 真正成为教学主体。 (2) 教具：多媒体、几何画板、小制作.
根据导数的定义总结出这个新函数的求解方法
吗？
1、动手实践，探 究发现，培养学 生知识迁移提炼 能力； 2、分组讨论，锻 炼学生的团队意 识； 3、知识点展示， 提醒同学们重点 关注.
1、导数的几何意义：函数f(x)在
x=x0处的导数f′(x)的几何意义 就是函数f(x)的图像在x=x0处的 切线的斜率。即：
l0
0 t3 t4 t0
t1 t2 l2
t l1
东莞市樟木头中学 李鸿艳
教材 说明 分析 反思
教学 目标
板书 设计
教学过程 设计意图
重点与 难点 教学方法 与手段
教材分析
导数是微积分的核心概念之一，它为研究变量 和函数提供了重要的方法。《导数的几何意义》从 形的角度即割线入手，定义了切线，获得了导数的 几何意义。通过学习，可以帮助学生更好的理解导 数的概念及导数是研究函数的单调性、极值等性质 最有效的工具。与旧教材相比，新教材用形象直观 的“逼近”方法得到导数的几何意义，更有利于学 生对知识的理解和掌握。
▲问(一)：平面几何中我们怎样
判断直线是否是圆切线(图1)? ▲问(二)：如图直线l1是曲线C的 切线吗? l2能叫做过点P的曲2 l1
y=f(x)
o
x
图2
固旧引新， 为引入“导 数的几何意 义”奠定基 础.
▲问(三)求导数f′(x0)的步 骤有哪几步? ▲问(四)：平均变化率
教法 分析
(1)本节课采用的教法有：多媒体教学法、探究 发现法、分组讨论法。理论依据：利用多媒体 展示导数就是切线斜率的过程，让学生体会逼 近的思想方法，使问题变得直观，易于突破难 点。通过“动手探索、讨论验证、实践应用”， 让学生体验动手乐趣，增强参与意识，使他们 真正成为教学主体。 (2) 教具：多媒体、几何画板、小制作.
根据导数的定义总结出这个新函数的求解方法
吗？
1、动手实践，探 究发现，培养学 生知识迁移提炼 能力； 2、分组讨论，锻 炼学生的团队意 识； 3、知识点展示， 提醒同学们重点 关注.
1、导数的几何意义：函数f(x)在
x=x0处的导数f′(x)的几何意义 就是函数f(x)的图像在x=x0处的 切线的斜率。即：
导数的几何意义说课PPT课件
学生分组讨论交流，计算切 观，易于突破难点；学生在过程中，
点的导数值，自主合作探求 可以体会逼近的思想方法。最后的
导数与斜率的关系，教师请 证明环节，能够同时从数与形两个 学生证明导数就是切线斜率。 角度强化学生对导数概念的理解。
2020年10月2日
20
2020年10月2日
1
教材分析
教法分析
教学目标
教学过程
评价反思
一. 教材分析
（1） 教材的地位和作用 （2）重点难点 （3） 课时安排
一. 教材分析
（一）教材的地位和作用
微积分学是人类思维的伟大成果之一，是人类经历 了2500多年震撼人心的智力奋斗的结果，它开创了 向近代数学过渡的新时期 ，为研究变量和函数提 供了重要的方法。导数是微积分的核心概念之一， 有极其丰富的实际背景和广泛的应用。导数的几何 意义是学生在学习了瞬时变化率就是导数之后的内 容，通过这部分内容的学习，可以帮助学生更好的 理解导数的概念及导数是研究函数的单调性、变化 快慢和极值等性质最有效的工具，是本章的关键内 容。
2020年10月2日
10
二. 教法分析
（四）具体措施
根据以上的分析，本节课采用教师引导与学生 自主探究相结合，交流与练习相穿插的活动课 形式，以学生为主体，教师创设和谐、愉悦的 环境及辅以适当的引导。同时，利用多媒体形 象动态的演示功能提高教学的直观性和趣味性， 以提高课堂效率。教学中注重数形结合，从形 的角度对概念理解和运用。在这个过程中培养 学生分析解决问题的能力，培养学生讨论交流 的合作意识。
二. 教法分析
（二）教学方法
1、多媒体辅助教学 借助多媒体教学手段引导学生发现切线斜率 与该点导数值之间的关系，使问题变得直观，易 于突破难点；利用多媒体向学生展示导数就是切 线斜率的过程，体会逼近的思想方法。 2、探究发现法教学 让学生通过动手操作课件经历“实验、探索、论 证、应用”的过程，体验从特殊到一般的认识规 律，通过学生“动手、动脑、讨论、演练”增加 学生的参与机会，增强参与意识，教给学生获取 知识的途径，思考问题的方法，使学生真正成为 教学主体。
精选 《导数的概念及其几何意义》完整版教学课件PPT
的切线的斜率
点 处 的切 线方 程 .(数学
导函数的概念
抽象、直观想象、数学运
算)
激趣诱思
知识点拨
跳水运发动的跳台距水面高度分为5米、7.5米和10米3种,奥运会
、世界锦标赛等限用10米跳台.跳台跳水根据起跳方向和动作结构
分向前、向后、向内、反身、转体和臂立6组.比赛时,男子要完成
4个有难度系数限制的自选动作和6个无难度系数限制的自选动作,
不同?
提示:曲线f(x)在点(x0,f(x0))处的切线,点(x0,f(x0))一定是切点,只要求
出k=f'(x0),利用点斜式写出切线方程即可;而曲线f(x)过某点(x0,y0)
的切线,给出的点(x0,y0)不一定在曲线上,即使在曲线上也不一定是
切点.
激趣诱思
知识点拨
(3)曲线在某点处的切线是否与曲线只有一个交点?
D.0
)
2
(2)求函数 f(x)=- 的导数.
(0+x)2 -3(0+x)-02 +3×0
(1)解析:f'(0)= lim
x
Δ→0
(Δ)2 -3Δ
=
= lim (Δx-3)=-3.
Δ
Δ→0
x→0
答案:C
y
(2)解:f'(x)= lim x
Δ→0
= lim
Δ→0
2·Δ
-x
Δ→0
x→0
(0 +Δ)-(0)
f(x)在 x0 处可导,所以由导数的定义得
=f'(x0),故
Δ
x→0
(0 -Δ)-(0 )
lim
=-f'(x0).
点 处 的切 线方 程 .(数学
导函数的概念
抽象、直观想象、数学运
算)
激趣诱思
知识点拨
跳水运发动的跳台距水面高度分为5米、7.5米和10米3种,奥运会
、世界锦标赛等限用10米跳台.跳台跳水根据起跳方向和动作结构
分向前、向后、向内、反身、转体和臂立6组.比赛时,男子要完成
4个有难度系数限制的自选动作和6个无难度系数限制的自选动作,
不同?
提示:曲线f(x)在点(x0,f(x0))处的切线,点(x0,f(x0))一定是切点,只要求
出k=f'(x0),利用点斜式写出切线方程即可;而曲线f(x)过某点(x0,y0)
的切线,给出的点(x0,y0)不一定在曲线上,即使在曲线上也不一定是
切点.
激趣诱思
知识点拨
(3)曲线在某点处的切线是否与曲线只有一个交点?
D.0
)
2
(2)求函数 f(x)=- 的导数.
(0+x)2 -3(0+x)-02 +3×0
(1)解析:f'(0)= lim
x
Δ→0
(Δ)2 -3Δ
=
= lim (Δx-3)=-3.
Δ
Δ→0
x→0
答案:C
y
(2)解:f'(x)= lim x
Δ→0
= lim
Δ→0
2·Δ
-x
Δ→0
x→0
(0 +Δ)-(0)
f(x)在 x0 处可导,所以由导数的定义得
=f'(x0),故
Δ
x→0
(0 -Δ)-(0 )
lim
=-f'(x0).
《导数的几何意义》一等奖说课稿
《导数的几何意义》一等奖说课稿《《导数的几何意义》一等奖说课稿》这是优秀的说课稿文章，希望可以对您的学习工作中带来帮助！1、《导数的几何意义》一等奖说课稿我说课的内容是高中数学人教B版选修2-2中第一章第三节的内容——导数的几何意义第一课时。
就本课节教学实践，我将从以下八方面介绍我对本节课的教学设想：说考纲；说教材；说学情；说教法；说学法；说教学过程；说板书设计；说自评反思。
一、说考纲由于导数是微积分的核心概念之一，它为研究函数性质提供了有效的工具。
近年高考对导数加大了考查力度，不仅体现在解题工具上，更着力于思维取向的考查，它像一条腾跃的龙和开屏的凤，潜移默化地改变着我们思考问题的习惯。
数学思想的引领，辩证思想的渗透，帮助着我们确立科学的思维取向。
正因如此，导数的几何意义是整个导数及其应用部分中，新课标考纲唯一一个冠以“理解”的要求标准，也是这部分认知领域的最高标准，可见其地位和意义。
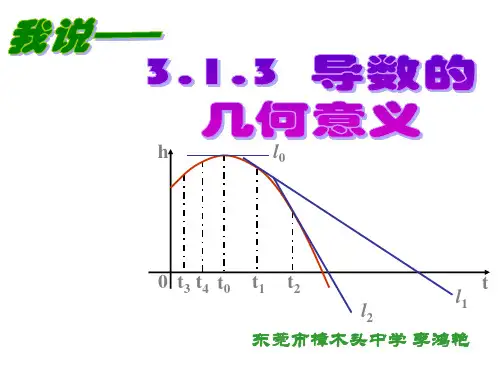
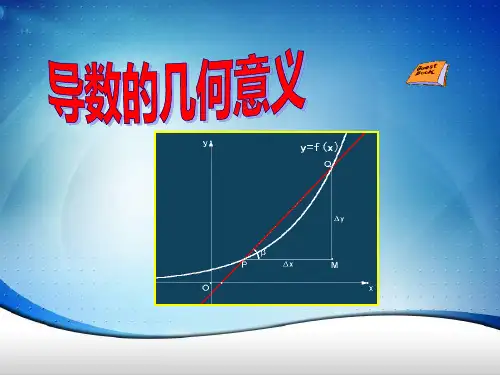
二、说教材教材从数形结合的思想即割线入手，以形象直观的“逼近”方法定义了切线，获得导数的几何意义，学生通过观察、思考、发现、归纳、运用形成完整概念，辩证思想得以渗透，有利于学生对知识的理解和掌握。
本节知识内容相当少，但在本节的教学实践中要突出其承前（进一步理解导数的定义，探讨函数值变化快慢）启后（作为研究函数的单调性、求解函数的极值和最值等性质最有效的工具）的关键纽带作用。
三、说学情通过前两节对函数平均变化率和导数定义的学习，学生对有关导数的问题已经有了初步的认识，但是由于导数定义的抽象性，学生认知起来仍具有一定的困难。
本节要通过动态的课件演示，将函数的平均变化率、导数（瞬时变化率）定义生动地展现，同时挖掘切线的斜率（斜率的绝对值的大小与陡峭程度）与函数图像的走势（导数的绝对值的大小与函数值变化快慢）的关联，成为后面研究函数的单调性、求解函数的极值和最值，探讨函数值变化快慢等性质最有效的工具。
激发学生的学习兴趣，提升独立探索、解决问题的能力、数形结合的能力及对知识灵活运用的能力。
导数的几何意义说课课件(中职教育)
导数的几何意义
学情分析
从知识上看，学生通过学习平均变化率，特别是函数的瞬时变化 率及导数的概念，对导数概念有一定的理解和认识，导数是对变化率的一种 “度量”，也在思考导数的另一种体现形式——形，学生对曲线的切线有一 定的认识，特别是初中学习圆与直线关系时，对切线有一定的了解与认 识．从学习能力上看，通过一年多的学习实践，学生掌握了一定的探究问题 的经验，具有一定的想象能力和研究问题的能力．从学习心理上看，学生已 经掌握了圆的切线，只是它的含义是公共点个数方面了解的，当然在思维方 面，形成了定势：直线与圆相切，直线与圆只有一个公共点．本节课切线的 含义 ，不是从公共点上定义切线，而是由 “割线”的“逼近”来定义曲线的 切线，把曲线的切线上升到新的思维层面上．通过概念的建立，概念的辨析， 问题的探究来激发学生的好奇心和学习兴趣． 本节课内容蕴含着导数的数、形两种体现形式，“逼近”的思想、 “以直代曲”思想、“数形结合”思想和用已知探究未知的思考方法．在教 学过程中应重视并体现这些数学思想方法．根据本节课内容特点，教学过程 中可充分借用信息技术这一辅助手段，利用FLASH的动态作图这一优势平台 为学生的问题探究，概念形成，思维过程提供支持．
导数的几何意义
教学目标 知识目标：
（1）理解导数的几何意义，初步体会“以直代曲”的辩证思想； （2）掌握求曲线上一点出的切线的斜率地方法。 能力目标： （1）培养学生的观察、动手动脑、归纳总结的能力； （2）培养学生合作学习、创新能力。 情感目标： （1）经过FLASH动画演示割线“逼近”成切线过程，让学生感受 函数图像的切线“形成”过程，获得函数图像的切线的意义； （2）增强学生问题应用意识教育，让学生获得学习数学的兴趣与 信心．
导数的几何意义
重点、难点
导数的几何意义 课件
x0
x
＝lim［(x)2＋3x x＋3x2］＝3x2. x0
令3x2＝3，得x＝±1，
所以点P的坐标为(1,1)或(－1，－1).
答案:(1,1)或(－1，－1)
2.(1)设直线l与曲线C的切点为(x0，y0)，
因为 y＝lim (x＋x)3－(x＋x)2＋1－(x3－x2＋1)＝3x2－2x，
x0
3
lim
x0
1 3
(
x
0
x)3 x
1 3
x
3 0
x 0 2，
所以切线方程为
y
1 3
x
3 0
x
2 0
(x
x0 )，
又因为切线过点A(1,0),所以
0
1 3
x
3 0
x
2 0
(1
x0 ),
化简得
2 3
x
3 0
x0解2 得0,x0=0或
x0
3 2
.
①当x0=0时，所求的切线方程为：y=0;
②当x0
时3 ，
【解题探究】1.曲线上一点切线的斜率与该点的导数有什么 关系? 2.切点的坐标满足切线方程吗？是否也满足曲线的方程？ 探究提示： 1.曲线上一点切线的斜率就是该点的导数. 2.切点的坐标既满足切线方程，同时也满足曲线的方程.
【解析】1.因为y＝x3，所以 y＝lim (x＋x)3－x3
x0
x
＝lim (x)3＋3x (x)2＋3x2 x
3 27
将切点坐标 (－1，2代3入) 直线y＝x＋a，
3 27
得 a＝ 23＋1故＝32， a＝32 .
27 3 27
27
(2)由(1)知切点坐标是 (－1，23).
导数的几何意义说课(修改稿)PPT课件
利用逼近思想，掌握数形结合 ，类比推理的数学方法.
加强学生对“导数的几何意义 ”形象、直观的理解，将学生的 感知体验与抽象思维有效结合,提 高学生的思维能力.
归纳、总结解题步骤.
训练环节
教学 环节
内容
师生活动
设计意图
训练 环节
20 分钟 左右
一．基础练习 1.如图，试描述函数f(x) 在 x= -4,-2,0,2 附近函数 值的大小的变化情况. 2.下列函数中，f (1) >0的是( )
2.过程与方法目标：
通过观察图形、多媒体展示，使学生感 受切线的形成过程，掌握从具体到抽象，特殊 到一般的思维方法；领悟极限思想和函数思想.
3.情感、态度与价值观目标：
通过教学让学生认识导数知识解决问题的 优越性，激发学生的学习兴趣，培养主动学习 的态度，树立唯物主义思想观.
教师：
展示三 维目标
学生：
3.教法、学法分析
教法分析
1
为了培养学生 自主学习的能力 并且使不同层次 的学生都能得到 充分的发展，本 节课采用的教学 程序是： 先学后教，当堂 训练.
2
为了培养学生 的分析问题、解 决问题的能力及 合作精神和分享 意识本节课对疑 难问题展开小组 讨论，并采用“ 兵教兵”的教学 方法.
3
为增强教学效 果的直观性，帮 助学生更好地理 解无限逼近思想 ，揭示导数的几 何意义，本堂课 采用多媒体辅助 教学, 以突出重点 和突破难点
②数 f (x)在点P(x0 ,y0 )处的导数 f '(x0 )的几何意义是什么？
③函通过观察跳水问题中曲线 h(t)的切线斜率的变化情况,你得 到了哪些结论?
④ f '(x ), y' , f '(x0 ), y' │x-x0
加强学生对“导数的几何意义 ”形象、直观的理解，将学生的 感知体验与抽象思维有效结合,提 高学生的思维能力.
归纳、总结解题步骤.
训练环节
教学 环节
内容
师生活动
设计意图
训练 环节
20 分钟 左右
一．基础练习 1.如图，试描述函数f(x) 在 x= -4,-2,0,2 附近函数 值的大小的变化情况. 2.下列函数中，f (1) >0的是( )
2.过程与方法目标：
通过观察图形、多媒体展示，使学生感 受切线的形成过程，掌握从具体到抽象，特殊 到一般的思维方法；领悟极限思想和函数思想.
3.情感、态度与价值观目标：
通过教学让学生认识导数知识解决问题的 优越性，激发学生的学习兴趣，培养主动学习 的态度，树立唯物主义思想观.
教师：
展示三 维目标
学生：
3.教法、学法分析
教法分析
1
为了培养学生 自主学习的能力 并且使不同层次 的学生都能得到 充分的发展，本 节课采用的教学 程序是： 先学后教，当堂 训练.
2
为了培养学生 的分析问题、解 决问题的能力及 合作精神和分享 意识本节课对疑 难问题展开小组 讨论，并采用“ 兵教兵”的教学 方法.
3
为增强教学效 果的直观性，帮 助学生更好地理 解无限逼近思想 ，揭示导数的几 何意义，本堂课 采用多媒体辅助 教学, 以突出重点 和突破难点
②数 f (x)在点P(x0 ,y0 )处的导数 f '(x0 )的几何意义是什么？
③函通过观察跳水问题中曲线 h(t)的切线斜率的变化情况,你得 到了哪些结论?
④ f '(x ), y' , f '(x0 ), y' │x-x0
精选 《导数的概念及其几何意义》完整版教学课件PPT
要点二 导数的几何意义
对于曲线 y＝f(x)上的点 P0(x0，f(x0))和 P(x，f(x))，当 点 P0 趋 近于点 P 时，割线 P0P 趋近于确定的位置，这个确定位置的直线 P0T 称为点 P0 处的___切__线___．割线 P0P 的斜率是__k_＝__f_xx_－－__fx_0x_0___．当 点 P 无限趋近于点 P0 时，k 无限趋近于切线 P0T 的斜率．因此，函 数 f(x) 在 x ＝ x0 处 的 导 数 就 是 切 线 P0T 的 __斜__率__k__ ， 即 k ＝ _l_iΔ_mx_→0__f_x_0_＋__ΔΔ_xx_－__f_x_0_ ____.
∴a＝－5.
答案：(2)－5
题型二 求曲线的切线方程——师生共研 例 2 已知曲线 y＝13x3，求曲线在点 P(3,9)处的切线方程．
解析：由 y＝13x3，
得 y′＝li m Δx→0
ΔΔyx＝liΔmx→0
13x＋Δx3－13x3 Δx
＝13liΔmx→0 3x2Δx＋3xΔΔxx2＋Δx3＝13liΔmx→0[3x2＋3xΔx＋(Δx)2]＝x2，
解析：设切点坐标为(x0，y0)．
f′(x)＝li m Δx→0
fx＋Δx－fx Δx
＝li m Δx→0
x＋Δx2＋6－x2＋6 Δx
＝li m (2x＋Δx)＝2x. Δx→0
∴过(x0，y0)的切线的斜率为 2x0.
(1)∵切线与直线 y＝4x－3 平行，∴2x0＝4，x0＝2，
y0＝x20＋6＝10，
(1)先由已知求出 l1 的斜率，再由 l1⊥l2，求出 l2 的斜率，进而 求出切点坐标，得出 l2 的方程．
(2)求出 l1 与 l2 的交点坐标，l1，l2 与 x 轴的交点，求出直线 l1， l2 和 x 轴围成的三角形的面积．
导数的几何意义 课件
1 85
,
6 12
.
(2)因为切线平行于直线6x-y-2=0,
所以切线的斜率为6,即f'(x0)=6x0=6,得x0=1.
所以该点的坐标为(1,10).
(3)因为切线与直线x+12y-3=0垂直,
所以切线的斜率为12,即f'(x0)=6x0=12,得x0=2.
所以该点的坐标为(2,19).
反思解答此类题目,所给的直线的倾斜角或斜率是解题的关键,由
切线与x轴正方向的夹角为钝角;若f'(x0)=0,则切线与x轴平行或重
合.
2.“用割线的极限位置来定义切线”和“与曲线只有一个公共点的
直线是切线”的区别是什么?
剖析:在初中我们学习过圆的切线:当直线和圆有唯一公共点时,
我们称直线和圆相切,这时直线叫做圆的切线,唯一的公共点叫做
切点,圆是一种特殊的曲线.如果将圆的切线推广为一般曲线的切
点斜式方程求切线方程;解答第(2)小题,可把第(1)小题中求得的直
线方程与已知的曲线方程组成方程组,求方程组的解.
解:(1)将 x=2 代入曲线 C 的方程,得 y=4,
∴切点的坐标为(2,4).
y
Δx→0 x
∴y'|x=2= lim
=
1 (2 + Δx)3 + 4 - 1 × 23 - 4
需注意f'(x0)与f'(x)的意义不同,f'(x)为f(x)的导函数,而f'(x0)为f(x)在
x=x0处的导函数值.
区别
f'(x0)是具体的值,是数
值
f'(x)是 f(x)在某区间 I
f'(x) 上每一点都存在导数
高中数学《导数的几何意义》说课稿
导数的几何意义第一课时说课数学组杜老师我说课题目是高中数学人教B版选修2-2中第一章第三节的内容——导数的几何意义第一课时。
下面我从教材分析、学情分析、教学目标、教学过程、学法指导、课后反思等几部分进行说课。
一、教材分析：微积分学是人类思维的伟大成果之一，它开创了向近代数学过渡的新时期，为研究变量和函数提供了重要的方法。
选修2-2第一章导数是微积分的核心概念之一，有及其丰富的实际背景和广泛的应用。
导数的几何意义是学生学习了平均变化率、瞬时变化率以及导数的定义的基础上，进一步从几何角度理解导数的含义与价值的内容，是可以充分应用信息技术进行概念教学与问题探索的内容。
通过本节学习可以进一步体会数形结合以及特殊到一般的思想方法，是本章的关键内容。
二、学情分析：从知识上看，学生已经通过实例经历了由平均变化率到瞬时变化率刻画现实问题的过程，体会了量变引起质变的极限思想，理解了瞬时变化率就是导数，体会了导数的思想和实际背景，但是这些都是建立在数的基础上的，学生也渴求了解导数的另一种体现形式——形；从学习能力上看，学生通过一年多的高中数学学习，已经掌握了一定的探究问题的经验，具有了一定的想象能力和研究问题的能力；从学习心理上看，学生对曲线的切线认识有一定的思维定势——“与曲线仅有一个交点的直线是曲线的切线”。
在本节课中，我们要在概念上上升一个层次，即由割线的逼近来定义曲线的切线，在新的思维层面上研究曲线的切线，以此激发学生的好奇心和兴趣点。
三、教学目标：《课程标准》指出，在本模块中，“学生体会导数的思想及其丰富内涵，感受导数在解决实际问题中的作用，了解微积分的文化价值”。
基于这样的要求和学生知识、能力储备的情况，确立如下教学目标：知识与技能目标：了解一般曲线切线的定义，理解导数的几何意义，会求简单曲线在某点的切线斜率及切线方程。
过程与方法目标：通过割线逼近形成切线的动画演示过程，感受极限的思想方法；通过类比平均变化率的几何意义总结导数的几何意义的过程，体会类比推理的数学研究方法；学会用导数的几何意义研究曲线切线的斜率和方程的方法，体会数形结合、特殊到一般的研究问题的方法。
人教版数学高二《导数的几何意义》精品课件
-1-
• [解] 设杯中水的高度与时间t的函数关
系式为h＝f(t)．
• 在图(1)中，未满水之前，杯中水的高度 的瞬时变化率是一个常数，即：h′＝f′(t) 是一个常数，说明杯子的直径相同，故 形状为：
•
• 在图(2)中，未满水之前，h＝f(t)的图象 是一条下凸的曲线，即曲线的斜率逐渐 增大，说明杯子的直径由大变小，故形 状为：
叫做f(x)在开区间(a，b)内的导函数，记
作f′(x)或y′.
-1-
• (4)函数y＝f(x)在x0处的导数f′(x0)就是导函 数f′(x)在x＝x0处的函数值，即f′(x0)＝ f′(x)|x＝x0.
• 所以，求函数在一点处的导数，一般是 先求出函数的导函数，再计算这点的导 函数值．
-1-
• 3．利用导数的几何意义求曲线切线方程
• 4．利用导数的几何意义，求在点(x0， f(x0))处的切线方程的一般方法，可分两 步：
• (1)⑥__________________________； • (2)⑦__________________________.
-1-
• 自我校对：①函数f(x)在x＝x0处的瞬时变 化率 ②在x＝x0附近的变化情况 ③曲 线y＝f(x)在点P(x0，f(x0))处的切线斜率 ④y－f(x0)＝f′(x0)(x－x0) ⑤运动物体在 时刻x0的速度 ⑥先求出函数y＝f(x)在点 x0处的导数f′(x0) ⑦根据点斜式得切线方 程为y－y0＝f′(x0)(x－x0)
-1-
[解] (1)由y＝13x3得，
Δy＝13(x＋Δx)3－13x3
＝13[3x2Δx＋3x(Δx)2＋(Δx)3]，
ΔΔyx＝13[3x2＋3xΔx＋(Δx)2]，
• [解] 设杯中水的高度与时间t的函数关
系式为h＝f(t)．
• 在图(1)中，未满水之前，杯中水的高度 的瞬时变化率是一个常数，即：h′＝f′(t) 是一个常数，说明杯子的直径相同，故 形状为：
•
• 在图(2)中，未满水之前，h＝f(t)的图象 是一条下凸的曲线，即曲线的斜率逐渐 增大，说明杯子的直径由大变小，故形 状为：
叫做f(x)在开区间(a，b)内的导函数，记
作f′(x)或y′.
-1-
• (4)函数y＝f(x)在x0处的导数f′(x0)就是导函 数f′(x)在x＝x0处的函数值，即f′(x0)＝ f′(x)|x＝x0.
• 所以，求函数在一点处的导数，一般是 先求出函数的导函数，再计算这点的导 函数值．
-1-
• 3．利用导数的几何意义求曲线切线方程
• 4．利用导数的几何意义，求在点(x0， f(x0))处的切线方程的一般方法，可分两 步：
• (1)⑥__________________________； • (2)⑦__________________________.
-1-
• 自我校对：①函数f(x)在x＝x0处的瞬时变 化率 ②在x＝x0附近的变化情况 ③曲 线y＝f(x)在点P(x0，f(x0))处的切线斜率 ④y－f(x0)＝f′(x0)(x－x0) ⑤运动物体在 时刻x0的速度 ⑥先求出函数y＝f(x)在点 x0处的导数f′(x0) ⑦根据点斜式得切线方 程为y－y0＝f′(x0)(x－x0)
-1-
[解] (1)由y＝13x3得，
Δy＝13(x＋Δx)3－13x3
＝13[3x2Δx＋3x(Δx)2＋(Δx)3]，
ΔΔyx＝13[3x2＋3xΔx＋(Δx)2]，
导数几何意义应用说课课件
投影仪 屏幕
变式： 引申： 构造函数
分类讨论
数形结合
板书设计
说评价
通过教学设计中的归纳总结和反馈练习环节，要求学生自行 归纳总结本课重、难点，并对知识加以运用。教师选择学生 代表发言表达，在此过程中加强对学生观察能力，独立思考 能力，理解归纳能力，及数形结合能力的训练。并且注重师 生，生生之间的合作交流，及时对学生所取得的成绩进行肯 定，从而使学生获得成就感。增强其自信心，激发学生对数 学的求知欲望。通过对练习题的探究完成知识的迁移。并通 过设置分层作业为学生进一步探讨导数的应用指出方向，使 学生能更好的把握前后知识之间的联系，为下一步的学习奠 定了基础。
质是求解切点坐标的认识。
说教学设计
变式：已知函数 y f (x) x3 x 的图像是曲线C，求曲线C在点
M (t, f (t))处的切线方程。 【设计意图】通过前一环节的热身，学生明确求“过 “某点切线方程的步骤：（1）设切点，（2）求斜率 （含参），（3）点斜式写切线方程（含参），（4） 过已知点，建立方程，求切点。学生通过前面的经验 ，独立写出含有t的函数的切线方程，叫组长代表小组 回答，教师在黑板上写出简要步骤，给引申以提示。
说模式
《新课程标准》的理念是“向学生提供充分从事数学 活动的机会，帮助他们在自主探索和合作交流的过程中真 正理解和掌握基本的数学知识和技能，数学思想和方法”。
考虑授课对象是高二年级文科生，数学的知识基础和 数学思维能力的层次差异较大，所以本节课设计为分组合 作、自主实践的数学复习课教学模式。分组合作体现在学 生分为每四人一组，每组按照异质分组即每组均有各层次 水平学生，由相对较差的学生担任组长，这样的做法是为 了避免好学生一言堂，给学习后进的同学展示自我的机会。 调动所有学生的积极性，在探索的过程中都有感知和发现， 同时增加课堂容量，从实处构建高效课堂。
( 人教A版)导数的几何意义课件 (共35张PPT)
[典例 2] (1)曲线 f(x)＝－x12在点 P 处的切线方程为 2x＋y＋3＝0，则点 P 的坐标为 ________． (2)曲线 f(x)＝2x2－x 在点 P 处的切线与直线 x＋y－1＝0 垂直，则点 P 的坐标为 ________．
[解析] (1)设切点 P 为(x0，y0)，则
k＝f′(x0)＝liΔmx→0
数．这样，当 x 变化时，f′(x)便是 x 的一个函数，我们称它为 f(x)的导函数(简称
fx＋Δx－fx _导__数__)．y＝f(x)的导函数有时也记作 y′，即 f′(x)＝y′＝_l_iΔ_mx_→_0_______Δ_x________.
[双基自测]
1．设 f′(x0)＝0，则曲线 y＝f(x)在点(x0，f(x0))处的切线( )
4．曲线 y＝12x2 在点(1，12)处的切线方程为________．
解析：∵f′(1)＝liΔmx→0
121＋Δx2－12 Δx
＝liΔmx→0 Δx＋Δ12xΔx2＝liΔmx→0 (1＋12Δx)＝1，
∴曲线在点(1，12)处的切线的斜率为 1，则切线
方程为 y－12＝1×(x－1)，即 y＝x－12. 答案：y＝x－12
f(x0))处的切线的 斜率 ，也就是曲线 y＝f(x)在点 P(x0，f(x0))处的切线斜率 k＝ _l_iΔ_mx_→_0__f_x_0_＋__Δ_Δx_x_－__f__x_0_＝ f′(x0) ，相应地，切线方程为 y－f(x0)＝f′(x0)(x－x0)．
二、函数 y＝f(x)的导函数 从求函数 f(x)在 x＝x0 处导数的过程可以看到，当 x＝x0 时，f′(x0)是一个 确定 的
(2)设切点 P 为(x0，y0)，则 k＝f′(x0)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
导数的几何意义
相
y yf(x) 交
P
o
x
教材分析 学情分析 教法学法 教学过程 板书设计
设计反思
教材分析 地位作用 重点难点 教学目标
本节内容是探求曲线上某点处切线的斜率和导数的关系 ，它介于导数的概念和导数的运算应用之间.通过本节的学 习，既有利于学生理解导数概念的本质内涵，又可以帮助学 生以后更好的体会导数是研究函数的单调性、变化快慢等性 质最有效的工具.起到了承上启下的作用.
奇心和学习兴趣.让学生带着问题进入本节课的探究
环节，使学生的学习目的更明确，积极性更高.
（ 二 ） 活动1 动手操作几何画板，动画演示，观察描述割线变 自 化规律，感知曲线在某点处的切线并描述曲线的切线定 主 义. 探 究
合
作
切线.gsp
学
习
（
二
） 活动2.表示出割线PQ的斜率并讨论分析在x 0 的
x
数
线斜率
作
学
习
设计意图：这一环节主要是让学生分别从“数”和“形”
两个角度发x现 0 时割线的变化情况，为了突破重难点，
我运用几何画板演示，使问题更直观，学生也可以体会逼近 的思想方法。
（三）学以致用 强化落实
例1 求抛物线f(x)=x2在点P(1,1)处的切线的斜率.
解：在点（ 1,1）切线的斜率是
y
学 以
P
2,
1 2
●
致
o x
用
（三）学以致用 强化落实
例 3 .求 抛 物 线 y = x 2过 点 5 2 ， 6 的 切 线 方 程 .
y
y x2
3, 9
P
5 2
,6
2 , 4 x0, x02
o
x
“曲线在点P的切线”与“曲线过点P的切线”一 样吗？
归纳总结：若点P不是切点，
(1)收集有关微积分创立的时代背景和有关人物的
资料。
作
业
(2)书面作业：课本P12，练习B第2题
布
课本P13，练习B第2题
置
(3)拓展作业：思考：经过一已知点的曲线切线方程如何求呢？
如 ： 求 y曲 1过 线(点 1,1)的 切 线 方 程 x
设计意图：作业（1）有助于拓宽学生视野，作业 （2）有助于学生掌握本节重点内容，作业（3） 帮助学生提高能力。既注重了“双基”，又照顾到 了学生的个体差异。
疑 求切线方程关键在于切点 难 的导数是直线的斜率，所 辨析 以设出切点是做题的关键
A P
0
B l1
x P
求曲线过点P的切线方程的分析思路：
（1）若点P不在曲线上，如例3，设出切点坐标，
再 次
利用切线的斜率，求出切点的坐标。代入点斜式， 求出切线的方程。
升 （2）若点P在曲线上，由于P点不一定是切点， 华 一般方法也同上
自 过程中，割线PQ的斜率变化规律.
主 探
针对学生在这个活动中可能出现的情况作出如下预设： 预设(1) 如果学生通过组内互相讨论分析得出结论，则让
究 小组选一名代表上讲台给大家展示
，
合 预设(2) 如果学生在小组讨论过程中不能发现规律并
作 学
有效地分析出结论，则教师及时给予点拨，进一步的 启发诱导学生思考，直至完成结论的推出。
） 切线的呢？
创 设 情 境
问题2.如图直线 y
l1是曲线C的切线吗?
l 2 呢?
l1
问题3 曲线在点P处
l2
A
切线用能用直线与切
B
线的公共点个数来定
，
导 入
0
义吗？ 那么对于一般 的曲线，切线该如何 x 寻找呢？
新 课 设计意图：本环节以问题串的形式引导学生的思维，
与圆的切线类比，引起认知上的冲突，激发学生的好
求在一点处切线方程的步骤
更 上
（1）求出函数在点x0处的变化率 f(x0)，得到 曲线在点(x0,f(x0))的切线的斜率。
一
层 （2）根据直线方程的点斜式写出切线方程，即
学以致用 强化落实
例2 求双曲线 y
1 x
在点
2,
1 2
的切线方程。
y
y x2
f (1) lim f (1 x) f (1)
x0
x
初
lim (1 x)2 1
次
x0
x
尝
lim 2x x)2 2
试
x0
x
P 1,1
o
x
因 此 ， 抛 物 线 y = f x = x 2 在 点 P 1 ， 1 处 的 切 线 斜 率 为 2 .
求切线方程呢？
（三）学以致用 强化落实
教材分析 教材地位 重点难点 教学目标
重点:导数的几何意义及应用. 难点:导数的几何意义的探求过程.
教材分析 教材地位 重点难点 教学目标
通过实验、探究导数的几何意义． 理解导数的几何意义，会求简单曲线在某点处的切线斜率 及切线方程.
在寻找切线新定义的过程中，使学生通过有限认识无限， 发现数学的美． 通过问题驱动，让学生在质疑、交流、讨论中形成良好的 数学思维品质．
（四） 归纳小结 深化提高
1.知识技能小结 2.思想方法小结
课
堂
设计意图：让学生回顾知识形成过程，强化学生
小
对概念的准确把握，深刻理解概念的应用，内化 数学思想方法，不仅让学生知道学了什么，还要
结
让学生清楚如何学，以便提高学生的解决问题能
力.
（五） 作业布置 课后延伸 课后思考及作业——拓展提高
D 若曲线yf(x)在点（x0, f (x0)）处的切线斜率不存在，则曲线
在该点处导数不存在。
2、求 y曲 2x21在 线P （ 点 -1,3）处的切线
3、求 y曲 x23x线 1在1 点 ,5 ） （ 处的切线
4、求 y曲 x23x线 1过点 2,5 ） （ 处的切线
设计意图：让学生明确自己掌握了哪些，是否还存在问题没有解决，同时也 让老师清楚自己的教学效果，明确哪些方面需要进一步完善，了解教学目标 的达成情况.
x
情 境 ，
第二步：当 x 趋近于0时，平均变化率
无限趋近于的常数就是 。
f(x0x)f(x0) x
导 入
f(x 0 ) li x m 0f(x 0 x x ) f(x 0 ) li x m 0 y x
新
课
设计意图:这是从“数”的角度描述导数，为探求导数的 几何意义做准备.
（
一 问题1.平面几何中我们是怎样判断直线是否是圆的割线或
设计意图：在例题的解决过程中，层层递进，一步步 提升学生的思维.最终掌握利用导数的几何意义研究曲 线的切线问题，从而轻松地解决本节重点。
课堂小测
1、下列说法正确的是 （ ）
A 若 f(x )不存y 在 f(x )在 ， x 0 ,点 f( 则 x 0 ) ） （ 曲 处 线 B 若y 曲 f(x )在 线 x 0 点 ,f(x 0 ) ） （ 处f有 (x )必 切 存 C 若 f(x)不存y 在 f(x)在 ， x 0 点 ,f则 (x 0 )） （ 曲 处 线 切
课题
例1
概念 例2
理解
例3
投影域 领 用 应
教学过程各环节的 时间分配
• 1.创设情境，导入新课（3分钟） • 2.自主探究，合作学习（16分钟） • 3.成果展示，汇报交流（10分钟） • 4.归纳总结，提升拓展（14分钟） • 5.反馈训练，巩固落实（7分钟）
• 总计45分钟。
设计反思
本节课在整个教学过程中学生以研究者的身 份学习，在问题解决的过程中，通过自身的体验 感 受 知 识 的 探 究 生 成 过 程 。教师在这个过程中始 终扮演学生学习的协作者和指导者。学生通过自 身的情感体验，能够很快的形成知识结构，转化 为数学能力。
教法与学法
教法
学法
情景 教学
问题 驱动
多媒 体辅
助
动手 尝试
观察 发现
合作 学习
教学过程
1 创设情境 导入新课
2
自主探究 合作学习 3 学以致用 强化落实
4 归纳小结 深化提高
5 布置作业 课后延伸
（
一
） 求导数 f(x0)的步骤是什么？
创 设
第一步：求平均变化 率 f(x0x)f(x0) ；
习
（
二 ） 自
活动3:你能从上述过程中概括出函数
导数 f (x0)的几何意义吗？
f (x) 在xx0处的
主
代数
几何
探 究
f(x0x)f(x0) x
函数 f在(x)x=x0附近小 区间内的平均变化率
割线斜率
， 合
lim f(x0x)f(x0) 函数 f (在x)x=x0处的导 曲线在x=x0处的切
x 0
通过探究过程中的讨论、交流、合作、实验操作等活动激 发学生学习数学的兴趣；培养学生合作学习和数学交流的能 力．
学情分析
1、从知识上看，学生已经理解了导数的概念，但 这是建立在“数”的基础上的，缺乏从“形”上去理 解导数. 2、从学习能力上看，学生具备了一定的探究问题 的能力，但缺乏自主探究的主动性，并且学生对 切线的认识有着一定的思维定势.
相
y yf(x) 交
P
o
x
教材分析 学情分析 教法学法 教学过程 板书设计
设计反思
教材分析 地位作用 重点难点 教学目标
本节内容是探求曲线上某点处切线的斜率和导数的关系 ，它介于导数的概念和导数的运算应用之间.通过本节的学 习，既有利于学生理解导数概念的本质内涵，又可以帮助学 生以后更好的体会导数是研究函数的单调性、变化快慢等性 质最有效的工具.起到了承上启下的作用.
奇心和学习兴趣.让学生带着问题进入本节课的探究
环节，使学生的学习目的更明确，积极性更高.
（ 二 ） 活动1 动手操作几何画板，动画演示，观察描述割线变 自 化规律，感知曲线在某点处的切线并描述曲线的切线定 主 义. 探 究
合
作
切线.gsp
学
习
（
二
） 活动2.表示出割线PQ的斜率并讨论分析在x 0 的
x
数
线斜率
作
学
习
设计意图：这一环节主要是让学生分别从“数”和“形”
两个角度发x现 0 时割线的变化情况，为了突破重难点，
我运用几何画板演示，使问题更直观，学生也可以体会逼近 的思想方法。
（三）学以致用 强化落实
例1 求抛物线f(x)=x2在点P(1,1)处的切线的斜率.
解：在点（ 1,1）切线的斜率是
y
学 以
P
2,
1 2
●
致
o x
用
（三）学以致用 强化落实
例 3 .求 抛 物 线 y = x 2过 点 5 2 ， 6 的 切 线 方 程 .
y
y x2
3, 9
P
5 2
,6
2 , 4 x0, x02
o
x
“曲线在点P的切线”与“曲线过点P的切线”一 样吗？
归纳总结：若点P不是切点，
(1)收集有关微积分创立的时代背景和有关人物的
资料。
作
业
(2)书面作业：课本P12，练习B第2题
布
课本P13，练习B第2题
置
(3)拓展作业：思考：经过一已知点的曲线切线方程如何求呢？
如 ： 求 y曲 1过 线(点 1,1)的 切 线 方 程 x
设计意图：作业（1）有助于拓宽学生视野，作业 （2）有助于学生掌握本节重点内容，作业（3） 帮助学生提高能力。既注重了“双基”，又照顾到 了学生的个体差异。
疑 求切线方程关键在于切点 难 的导数是直线的斜率，所 辨析 以设出切点是做题的关键
A P
0
B l1
x P
求曲线过点P的切线方程的分析思路：
（1）若点P不在曲线上，如例3，设出切点坐标，
再 次
利用切线的斜率，求出切点的坐标。代入点斜式， 求出切线的方程。
升 （2）若点P在曲线上，由于P点不一定是切点， 华 一般方法也同上
自 过程中，割线PQ的斜率变化规律.
主 探
针对学生在这个活动中可能出现的情况作出如下预设： 预设(1) 如果学生通过组内互相讨论分析得出结论，则让
究 小组选一名代表上讲台给大家展示
，
合 预设(2) 如果学生在小组讨论过程中不能发现规律并
作 学
有效地分析出结论，则教师及时给予点拨，进一步的 启发诱导学生思考，直至完成结论的推出。
） 切线的呢？
创 设 情 境
问题2.如图直线 y
l1是曲线C的切线吗?
l 2 呢?
l1
问题3 曲线在点P处
l2
A
切线用能用直线与切
B
线的公共点个数来定
，
导 入
0
义吗？ 那么对于一般 的曲线，切线该如何 x 寻找呢？
新 课 设计意图：本环节以问题串的形式引导学生的思维，
与圆的切线类比，引起认知上的冲突，激发学生的好
求在一点处切线方程的步骤
更 上
（1）求出函数在点x0处的变化率 f(x0)，得到 曲线在点(x0,f(x0))的切线的斜率。
一
层 （2）根据直线方程的点斜式写出切线方程，即
学以致用 强化落实
例2 求双曲线 y
1 x
在点
2,
1 2
的切线方程。
y
y x2
f (1) lim f (1 x) f (1)
x0
x
初
lim (1 x)2 1
次
x0
x
尝
lim 2x x)2 2
试
x0
x
P 1,1
o
x
因 此 ， 抛 物 线 y = f x = x 2 在 点 P 1 ， 1 处 的 切 线 斜 率 为 2 .
求切线方程呢？
（三）学以致用 强化落实
教材分析 教材地位 重点难点 教学目标
重点:导数的几何意义及应用. 难点:导数的几何意义的探求过程.
教材分析 教材地位 重点难点 教学目标
通过实验、探究导数的几何意义． 理解导数的几何意义，会求简单曲线在某点处的切线斜率 及切线方程.
在寻找切线新定义的过程中，使学生通过有限认识无限， 发现数学的美． 通过问题驱动，让学生在质疑、交流、讨论中形成良好的 数学思维品质．
（四） 归纳小结 深化提高
1.知识技能小结 2.思想方法小结
课
堂
设计意图：让学生回顾知识形成过程，强化学生
小
对概念的准确把握，深刻理解概念的应用，内化 数学思想方法，不仅让学生知道学了什么，还要
结
让学生清楚如何学，以便提高学生的解决问题能
力.
（五） 作业布置 课后延伸 课后思考及作业——拓展提高
D 若曲线yf(x)在点（x0, f (x0)）处的切线斜率不存在，则曲线
在该点处导数不存在。
2、求 y曲 2x21在 线P （ 点 -1,3）处的切线
3、求 y曲 x23x线 1在1 点 ,5 ） （ 处的切线
4、求 y曲 x23x线 1过点 2,5 ） （ 处的切线
设计意图：让学生明确自己掌握了哪些，是否还存在问题没有解决，同时也 让老师清楚自己的教学效果，明确哪些方面需要进一步完善，了解教学目标 的达成情况.
x
情 境 ，
第二步：当 x 趋近于0时，平均变化率
无限趋近于的常数就是 。
f(x0x)f(x0) x
导 入
f(x 0 ) li x m 0f(x 0 x x ) f(x 0 ) li x m 0 y x
新
课
设计意图:这是从“数”的角度描述导数，为探求导数的 几何意义做准备.
（
一 问题1.平面几何中我们是怎样判断直线是否是圆的割线或
设计意图：在例题的解决过程中，层层递进，一步步 提升学生的思维.最终掌握利用导数的几何意义研究曲 线的切线问题，从而轻松地解决本节重点。
课堂小测
1、下列说法正确的是 （ ）
A 若 f(x )不存y 在 f(x )在 ， x 0 ,点 f( 则 x 0 ) ） （ 曲 处 线 B 若y 曲 f(x )在 线 x 0 点 ,f(x 0 ) ） （ 处f有 (x )必 切 存 C 若 f(x)不存y 在 f(x)在 ， x 0 点 ,f则 (x 0 )） （ 曲 处 线 切
课题
例1
概念 例2
理解
例3
投影域 领 用 应
教学过程各环节的 时间分配
• 1.创设情境，导入新课（3分钟） • 2.自主探究，合作学习（16分钟） • 3.成果展示，汇报交流（10分钟） • 4.归纳总结，提升拓展（14分钟） • 5.反馈训练，巩固落实（7分钟）
• 总计45分钟。
设计反思
本节课在整个教学过程中学生以研究者的身 份学习，在问题解决的过程中，通过自身的体验 感 受 知 识 的 探 究 生 成 过 程 。教师在这个过程中始 终扮演学生学习的协作者和指导者。学生通过自 身的情感体验，能够很快的形成知识结构，转化 为数学能力。
教法与学法
教法
学法
情景 教学
问题 驱动
多媒 体辅
助
动手 尝试
观察 发现
合作 学习
教学过程
1 创设情境 导入新课
2
自主探究 合作学习 3 学以致用 强化落实
4 归纳小结 深化提高
5 布置作业 课后延伸
（
一
） 求导数 f(x0)的步骤是什么？
创 设
第一步：求平均变化 率 f(x0x)f(x0) ；
习
（
二 ） 自
活动3:你能从上述过程中概括出函数
导数 f (x0)的几何意义吗？
f (x) 在xx0处的
主
代数
几何
探 究
f(x0x)f(x0) x
函数 f在(x)x=x0附近小 区间内的平均变化率
割线斜率
， 合
lim f(x0x)f(x0) 函数 f (在x)x=x0处的导 曲线在x=x0处的切
x 0
通过探究过程中的讨论、交流、合作、实验操作等活动激 发学生学习数学的兴趣；培养学生合作学习和数学交流的能 力．
学情分析
1、从知识上看，学生已经理解了导数的概念，但 这是建立在“数”的基础上的，缺乏从“形”上去理 解导数. 2、从学习能力上看，学生具备了一定的探究问题 的能力，但缺乏自主探究的主动性，并且学生对 切线的认识有着一定的思维定势.