电容三点式振荡器Colpitts考毕兹

实验二 LC电容反馈式三点式振荡器一、实验目的1.熟悉电容三点式振荡器（考毕兹电路）、改进型电容三点式振荡器（克拉泼电路及西勒电路）的电路特点、结构及工作原理。

2.掌握振荡器静态工作点调整方法。

3.熟悉频率计、示波器等仪器的使用方法。

二、预习要求1.复习LC振荡器的工作原理。

2.分析图1电路的工作原理，及各元件的作用。

结合图2的等效电路，思考怎样跳线连接，才能构成三种不同的电容三点式振荡电路。

三、实验仪器设备1.双踪示波器2.频率计3.万用表4.TPE-GP5通用实验平台5.G1N实验模块四、实验原理及电路简介：1.实验原理：振荡器是一种在没有外来信号的作用下，能自动地将直流电源的能量转换为一定波形的交变振荡能量的装置。

根据振荡器的特性，可将振荡器分为反馈式振荡器和负阻式振荡器两大类，LC振荡器属于反馈式振荡器。

工作时它应满足两个条件：(1)相位条件：反馈信号必须与输入信号同相，以保证电路是正反馈电路，即电路的总相移Σφ=φk+φF=n×3600。

(2)振幅条件：反馈信号的振幅应大于或等于输入信号的振幅，即│ẢF│≥1，式中Ả为放大倍数，F为反馈系数。

当振荡器接通电源后，电路中存在着各种电的扰动（如热噪声、晶体管电流的突变等），它们就是振荡器起振的初始激励。

经过电路放大和正反馈的作用，它们的幅度会得到不断的加强。

同时，由于电路中LC谐振回路的选频作用，只有等于其谐振频率的电压分量满足振荡条件，最终形成了单一频率的振荡信号。

2.电路特点：图1为实验电路，V1001及周边元件构成了电容反馈振荡电路及石英晶体振荡电路。

V1002构成射极输出器。

S1001、S1002、S1003、J1001分别连接在不同位置时，就可分别构成考毕兹、克拉泼和西勒三种不同的LC振荡器以及石英晶体振荡器。

V1001V1002R 1001R1003R 1002R1008R 1007R 1006R1009C 1009C1006C 1001200P R 1005GNDGND S 1002300P 510P1000PS1004200P 100P 62P20P L 10016.2P62P100P1000P S100312J1001C1005Y 100110.7M H z C1007C1008P1001R p 1001SW1001R1010D1001GND +12VR p 1002C1010P1002GND图1 LC与晶体振荡器原理图12S1001C T 1001C1004C1003C10023. 思路提示：图2给出了几种振荡电路的交流等效电路图。

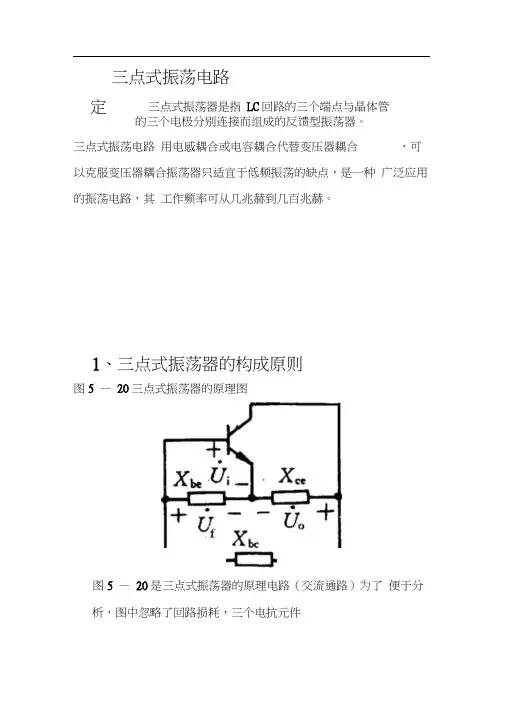
三点式振荡电路定三点式振荡器是指LC回路的三个端点与晶体管的三个电极分别连接而组成的反馈型振荡器。

三点式振荡电路用电感耦合或电容耦合代替变压器耦合，可以克服变压器耦合振荡器只适宜于低频振荡的缺点，是一种广泛应用的振荡电路，其工作频率可从几兆赫到几百兆赫。

1、三点式振荡器的构成原则图5 —20三点式振荡器的原理图图5 —20是三点式振荡器的原理电路（交流通路）为了便于分析，图中忽略了回路损耗，三个电抗元件X be 、X Ce 和X bC 构成了决定振荡频率的并联谐振回路要产生振荡，对谐振网络的要求：？必须满足谐振回路的总电抗 XbeX Ce X b^O ，回路呈现纯阻 性。

反馈电压U f 作为输入加在晶体管的 b 、e 极，输出U O 加 在晶体管的c 、e 之间，共射组态 为反相放大器，放大 器的的输出电压u o 与输入电压U i （即U f ）反相，而反馈 g Q电压U f 又是U o 在X bC> X be支路中分配在X be上的电压。

要满足正反馈，必须有为了满足相位平衡条件，U f 和U o 必须反相，由式（5.3.1）可知必有 孑 0成立，即X be 和X Ce 必须是同性质电抗，而XCeX b^ -（X be X Ce ）必为异性电抗。

综上所述，三点式振荡器构成的一般原则：（1）为满足相位平衡条件，与晶体管发射极相连X be(X be X bC )UoX be -X Ce U o(531)的两个电抗元件X be 、X Ce必须为同性， 而不与发射极相连的电抗元件X bC的电抗性质与前者相反，概括起来“射同基 反”。

此构成原则同样适用于场效应管电路，对应 的有“源同栅反”。

(2)振荡器的振荡频率可利用谐振回路的谐振频率来估算。

为容性的，称为电容三点式振荡器，也称为考比兹 振荡器(Colpitts)，如图5 — 21(a )所示；若与发射极相连的两个电抗元件X be 、X Ce为感性的，称为电感三点式振荡器，也称为哈 特莱振荡器(Hartley),如图5 — 21 (b )所 示。

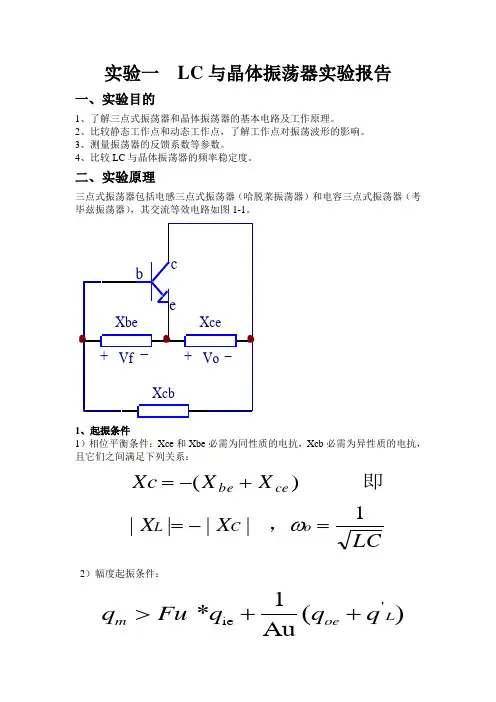
实验一 LC 与晶体振荡器实验报告一、实验目的1、了解三点式振荡器和晶体振荡器的基本电路及工作原理。

2、比较静态工作点和动态工作点，了解工作点对振荡波形的影响。

3、测量振荡器的反馈系数等参数。

4、比较LC 与晶体振荡器的频率稳定度。

二、实验原理三点式振荡器包括电感三点式振荡器（哈脱莱振荡器）和电容三点式振荡器（考毕兹振荡器），其交流等效电路如图1-1。

1、起振条件1）相位平衡条件：Xce 和Xbe 必需为同性质的电抗，Xcb 必需为异性质的电抗，且它们之间满足下列关系：2）幅度起振条件：LCX X X X Xc oC L cebe 1 |||| )(=-=+-=ω，即'ie 1*()AuL m oe q Fu q qq >++式中：qm ——晶体管的跨导， FU ——反馈系数， AU ——放大器的增益，qie ——晶体管的输入电导， qoe ——晶体管的输出电导， q'L ——晶体管的等效负载电导， FU 一般在0.1~0.5之间取值。

2、电容三点式振荡器1）电容反馈三点式电路——考毕兹振荡器图1-2是基本的三点式电路，其缺点是晶体管的输入电容Ci 和输出电容Co 对频率稳定度的影响较大，且频率不可调。

2）串联改进型电容反馈三点式电路——克拉泼振荡器电路如图1-3所示，其特点是在L 支路中串入一个可调的小电容C3，并加大C1和C2的容量，振荡频率主要由 C3和L 决定。

C1和C2主要起电容分压反馈作用，从而大大减小了Ci 和Co 对频率稳定度的影响，且使频率可调。

L1L13）并联改进型电容反馈三点式电路——西勒振荡器 电路如图1-4所示，它是在串联改进型的基础上，在L1两端并联一个小电容C4，调节C4可改变振荡频率。

西勒电路的优点是进一步提高电路的稳定性，振荡频率可以做得较高，该电路在短波、超短波通信机、电视接收机等高频设备中得到非常广泛的应用。

本实验箱所提供的LC 振荡器就是西勒振荡器。

实验3 电容三点式LC振荡器一、实验准备1．做本实验时应具备的知识点：●三点式LC振荡器●西勒和克拉泼电路●电源电压、耦合电容、反馈系数、等效Q值对振荡器工作的影响2．做本实验时所用到的仪器：●LC振荡器模块●双踪示波器●万用表二、实验目的1．熟悉电子元器件和高频电子线路实验系统；2．掌握电容三点式LC振荡电路的基本原理，熟悉其各元件功能；3．熟悉静态工作点、耦合电容、反馈系数、等效Q值对振荡器振荡幅度和频率的影响；4．熟悉负载变化对振荡器振荡幅度的影响。

三、实验电路基本原理1.概述ＬＣ振荡器实质上是满足振荡条件的正反馈放大器。

ＬＣ振荡器是指振荡回路是由ＬＣ元件组成的。

从交流等效电路可知：由ＬＣ振荡回路引出三个端子，分别接振荡管的三个电极，而构成反馈式自激振荡器，因而又称为三点式振荡器。

如果反馈电压取自分压电感，则称为电感反馈ＬＣ振荡器或电感三点式振荡器；如果反馈电压取自分压电容，则称为电容反馈ＬＣ振荡器或电容三点式振荡器。

在几种基本高频振荡回路中，电容反馈ＬＣ振荡器具有较好的振荡波形和稳定度，电路形式简单，适于在较高的频段工作，尤其是以晶体管极间分布电容构成反馈支路时其振荡频率可高达几百ＭＨＺ～ＧＨＺ。

2.ＬＣ振荡器的起振条件一个振荡器能否起振，主要取决于振荡电路自激振荡的两个基本条件，即：振幅起振平衡条件和相位平衡条件。

3.LC振荡器的频率稳定度频率稳定度表示：在一定时间或一定温度、电压等变化范围内振荡频率的相对变化程度，常用表达式：Δf０／f０来表示（f０为所选择的测试频率；Δf０为振荡频率的频率误差，Δf０＝f０２－f０１；f０２和f０１为不同时刻的f０），频率相对变化量越小，表明振荡频率的稳定度越高。

由于振荡回路的元件是决定频率的主要因素，所以要提高频率稳定度，就要设法提高振荡回路的标准性，除了采用高稳定和高Q值的回路电容和电感外，其振荡管可以采用部分接入，以减小晶体管极间电容和分布电容对振荡回路的影响，还可采用负温度系数元件实现温度补偿。

实验一 电容反馈三点式振荡器的实验研究一、实验目的1．通过实验深入理解电容反馈三点式振荡器的工作原理，熟悉改进型电容反馈三点式振荡器的构成及电路各元件作用；2．研究在不同的静态工作点时，对振荡器起振、振荡幅度和振荡波形的影响； 3．学习使用示波器和数字式频率计测量高频振荡器振荡频率的方法； 4．观察电源电压和负载变化对振荡幅度、频率及频率稳定性的影响。

二、实验原理电容反馈三点式振荡器的基本原理电路(考比兹振荡器)如图2-1(a)所示。

由图可知，反馈电压由C 1和C 2分压得到，反馈系数为211C C C B += (2-1)起振的幅度条件为p m g Bg 1>(忽略三极管g e ) (2-2) 其中，g m 为晶体管跨导，g p 为振荡回路的等效谐振电导。

图2-1(a)所示等效电路中的回路总电容为2121C C C C C +⋅= (2-3)振荡频率近似为LCf g π21≈(2-4)当外界条件(如温度等)发生变化时，振荡回路元件及晶体管结电容要发生变化，从而使得振荡频率发生漂移。

因此，为了改善普通电容反馈三点式振荡器的频稳度，可在振荡回路中引入串接电容C 3，如图2-1(b)所示，当满足C 3<< C 1、C 2时，C 3明显减弱了晶体管与振荡回路的耦合程度。

为了得到较宽的波段覆盖效果，引入并联电容C 4(它和C 3为同一个数量级)，回路总电容近似为C≈C 3+C 4。

这种改进型电容反馈振荡器称为西勒电路，其振荡频率为)(2143C C L f g +≈π (2-5)当改变C 4调节f g 时，振荡器的反馈系数不会受显著影响。

三、实验电路说明本实验电路采用西勒振荡器，如图2-2所示。

由图可知，电容C 1、C 2、C 3、C 4和电感L 1组成振荡回路。

晶体管VT 1的集电极直流负载为R C ，偏置电路由R 1、R 2、W 1和R e 构成，改变电位器W 1可改变VT 1的静态工作点。

1电容三点式振荡器—考毕兹（Colpitts ）振荡器图1给出两种电容三点式振荡器电路。

图中12b b R R 、和e R 为分压式偏置电阻，图1 电容三点式振荡器电路图（a ）电路中，三极管发射极通过E C 交流接地，是共射组态；图（b ）电路中，三极管基极通过b C 交流接地，是共基组态。

组态不同，但都满足“射同基反”的构成原则，即与发射极相连的两个电抗性质相同，不与发射极相连的是性质相异的电抗。

高频耦合和旁路电容(b c C C 、和E C 对于高频振荡信号可近似认为短路，旁路和耦合电容的容值至少要比回路电容值大一个数量级以上。

12L C C 、和构成并联谐振回路，12C C 和称为回路电容(也工作电容 。

2电容三点式振荡器电路的起振条件以图5 —22（b）所示共基组态的电容三点式电路为例分析起振条件。

(a)高频交流等效电路画高频振荡回路之前应仔细分析每个电容与电感的作用，应处理好以下问题：画高频振荡回路时，小电容是工作电容, 大电容是耦合电容或旁路电容, 小电感是工作电感, 大电感是高频扼流圈。

画等效电路时保留工作电容与工作电感, 将耦合电容与旁路电容短路, 高频扼流圈开路, 直流电源与地短路,通常高频振荡回路是用于分析振荡频率的，一般不需画出偏置电阻。

判断工作电容和工作电感, 一是根据参数值大小。

电路中数值最小的电容(电感和与其处于同一数量级的电容(电感均被视为工作电容(电感 , 耦合电容与旁路电容的数值往往要大于工作电容几十倍以上, 高频扼流圈的电感数值远远大于工作电感；二是根据所处的位置。

旁路电容分别与晶体管的电极和交流地相连，旁路电容对偏置电阻起旁路作用；耦合电容通常在振荡器负载和晶体管电路之间，起到高频信号耦合及隔直流作用。

这两种电容对高频信号都近似为短路。

工作电容与工作电感是按照振荡器组成法则设置的。

高频扼流圈对直流和低频信号提供通路, 对高频信号起阻隔作用。

图1（b ）的交流等效电路图5 —24（a ）电容三点式交流等效电路(b 起振条件和振荡频率起振条件包括振幅条件和相位条件。

1．2 电容三点式振荡电路设计图1所示为利用反馈原理设计的一个电容三点式振荡器，又称考毕兹振荡器。

图中晶体管放大电路构成主网络，直流电源对电路提供偏置，偏置电压经过直流工作点分析在电路中表示出来。

LC并联谐振回路构成正反馈选频网络，其中C1、C2和Ce分别为高频耦合电容和旁路电容，C3、C4为回路电容，L1是回路电感。

在不考虑寄生参数的情况下，根据正弦振荡的相位条件，振荡频率计算公式为：C4端接回基极构成正反馈，反馈系数为F=C3／C4。

电容三点式振荡器的优点为电容对晶体管非线性特性产生的高次谐波呈现低阻抗，所以反馈电压中高次谐波分量很小，因此输出波形接近于正弦波。

2 电路的仿真分析2．1 起振过程振荡曲线分析，即电路的瞬态分析(Time Domain Transient) 在Capture CIS中绘制电路的原理图如图1，各元件参数如图中所示。

对波形发生电路进行时域仿真就是仿真电路的输出波形，因此应选择瞬态分析方式。

仿真时间选择5 μs，并设置Maximum step(最大步长)为10 ns，以输出光滑的振荡波形。

执行仿真分析命令，可以在Probe中清晰地看出正弦波发生电路的起振过程。

图2即为out点输出波形，从中可见起振时间约为1．0 us。

根据仿真波形分析起振过程如下：在刚接通电源时电路中存在各种扰动，这些扰动均具有很宽的频谱，但是只有频率近似为LC选频网络谐振频率fo的分量才能通过反馈网络产生较大的反馈电压。

由于环路增益T>1，经过线性放大和反馈的不断循环，振荡电压会不断增大。

然而由于晶体管的线性范围是有限的，随着振幅的增大放大器逐渐进入饱和区或截止区，增益逐渐下降。

当放大器增益下降而导致环路增益下降到1时，振幅增长过程停止，振荡器达到平衡，进入等幅振荡状态。

改变横坐标将波形放大，利用标尺功能测得波形极大点时间坐标如图3中所示。

通过计算可发现波形周期不稳定：B-A=2．303 3-2．190 5=0．112 8 us，C-B=2．409 3-2．303 3=0．1060us，D-C=2．5107-2．409 3=0．101 4us，E-D=2．621 0-2．510 7=0．110 3 us；即波形频率fo稳定度不高fo=1／T≈4／(E-A)=9．29 MHz。

目录实验一 LC与晶体振荡器实验 (1)实验二通频带展宽实验 (6)实验三非线性波形变换实验 (11)实验四变容二极管调频器与相位鉴频器实验 (15)实验五幅度调制与解调实验 (20)实验六锁相调频与鉴频实验 (24)实验七函数信号发生实验 (30)实验八锁相环与锁相式数字频率合成器实验 (33)实验九数字调频与解调实验 (36)实验十数字信号发生实验 (39)实验十一集成乘法器混频实验 (42)实验十二小信号调谐放大实验 (45)实验十三电视图像中放检波实验 (49)实验十四电视伴音中放鉴频实验 (53)实验一 LC 与晶体振荡器实验一、实验目的1）了解电容三点式振荡器和晶体振荡器的基本电路及其工作原理。

2）比较静态工作点和动态工作点，了解工作点对振荡波形的影响。

3）测量振荡器的反馈系数、波段复盖系数、频率稳定度等参数。

4）比较LC 与晶体振荡器的频率稳定度。

二、实验预习要求实验前，预习教材：“电子线路非线性部分”第3章：正弦波振荡器；“高频电子线路”第四章：正弦波振荡器的有关章节。

三、实验原理说明三点式振荡器包括电感三点式振荡器（哈脱莱振荡 器）和电容三点式振荡器（考毕兹振荡器），其交流等效电路如图1-1。

1． 起振条件1）相位平衡条件：X ce 和X be 必需为同性质的电抗，X cb 必需为异性质的电抗，且它们之间满足下列关系：2）幅度起振条件：式中：q m ——晶体管的跨导，F U ——反馈系数， 图1-1 三点式振荡器 A U ——放大器的增益， q ie ——晶体管的输入电导， q oe ——晶体管的输出电导， q'L ——晶体管的等效负载电导， F U 一般在0.1~0.5之间取值。

2．电容三点式振荡器1）电容反馈三点式电路——考毕兹振荡器（a ）考毕兹振荡器 （b ）交流等效电路LCX X X X Xc o C L ce be 1 |||| )(=-=+-=ω，即)(Au1* 'ie L oe m q q q Fu q ++>图1-2 考毕兹振荡器图1-2是基本的三点式电路，其缺点是晶体管的输入电容C i 和输出电容Co 对频率稳定度的影响较大，且频率不可调。

高频振荡电路原理图解乐乐课堂振荡电路
高频电路中主要的信号产生器主要分为振幅和频率高度稳定的正弦波产生器和频率受电压调控的压控式正弦波振荡器两大类。

它们被广泛应用于各种通信设备中。

LC基本正弦波产生器
最基本的振荡电路的模型和工作原理如下所示，它可以由一个放大器K和一个反馈网络F的闭环组成。

通过适当选择反馈网络的电抗参数，就能调控振荡的频率。

电感三点式（哈脱莱Hartley）振荡电路
又称为电感反馈振荡电路，其中X2为反馈支路电感。

特点：与射极相连的X1、X2电抗性质同为电感；电路起振容易；最高振荡频率为几十兆赫；但波形和振荡频率稳定性差，改变电容量时频率刻度的变化量是非均匀的，调试和使用不方便。

电容三点式（考毕兹Colpitts）振荡电路
又称为电容反馈振荡电路，其中X2为反馈支路电容。

特点：与射极相连的X1、X2电抗性质同为电容；振荡频率稳定
性好；最高振荡频率为几百兆赫；但电路不易起振，改变电容量时频率刻度的变化量的非均匀性稍有改善。

改进型的电容三点式振荡电路（其中串联改进型称“克拉泼Clapp”振荡电路，并联改进型称“西勒Seiler”振荡电路）
特点：以电容三点式振荡电路为基础，在电感（L）支路中串一
小电容；振荡频率稳定性好；最高振荡频率为几百兆赫至几千兆赫；改变电容量时频率刻度的变化量为均匀变化；起振性能比起电容三点式有所改善：。

改进型电容三点式振荡电路的设计本次课设设计了改进型电容三点式高频振荡器，介绍了设计步骤，比较了各种设计方法的优缺点，总结了不同振荡器的性能特征。

使用Protel2004DXP 制作PCB 板，并使用环氧树脂铜箔板和FeCl 3进行了制板和焊接。

使用实验要求的电源和频率计进行验证，实现了设计目标。

关键词：电容三点式、西勒电路、Protel 、印制电路板1 实验原理1.1 振荡的原理三点式LC 正弦波振荡器的组成法则（相位条件）是：与晶体管发射极相连的两个电抗元件应为同性质的电抗，而与晶体管集电极—基极相连的电抗元件应与前者性质相反。

图1-1所示为满足组成法则的基本电容反馈LC 振荡器共基极接法的典型电路。

当电路参数选取合适，满足振幅起振条件时，电路起振。

当忽略负载电阻、晶体管参数及分布电容等因素影响时，振荡频率osc f 可近似认为等于谐振回路的固有振荡频率o f ，即osc f = （1）式中 C 近似等于1C 与2C 的串联值1212C C C C C ≈+ （2）图1-1 电容反馈LC 振荡器由图1-1所画出的分析起振条件的小信号等效电路如图1-2所示。

图1-2 分析起振条件的小信号等效电路 由图1-2分析可知，振荡器的起振条件为：e L e L m ng g ng g n g +=+>'''1)(1 （3） 式中 '011,//L e L e eg g R R r == 0e R 为LC 振荡回路的等效谐振电阻；电路的反馈系数 112f C k n C C =≈+ （4） 由式（3）看出，由于晶体管输入电阻e r 对回路的负载作用，反馈系数f k 并不是越大越容易起振，反馈系数太大会使增益A 降低，且会降低回路的有载Q 值，使回路的选择性变差，振荡波形产生失真，频率稳定性降低；所以，在晶体管参数一定的情况下，可以调节负载和反馈系数，保证电路起振。

f k 的取值一般在0.1—0.5 之间。

电容反馈式三段振荡器
考毕兹振荡器的典型电路见图。

有图的等效电路可知，本电路与哈特莱式很相似，只是利用电容C1和C2作为分压器，代替了哈特莱式中的L1和L2。

同样可以证明，这种电路满足产生振荡的相位条件。

经验证明，C1/C2取1/2~1/8较为适宜。

与电感三端振荡电路相比，电容三端振荡器的优点是输出波形较好，这是因为集电极和基极电流可通过对谐波为低阻抗的电容支路回到发射级，所以高次谐波反馈减弱，输出的谐波分量减小，波形更加接近于正弦波。

其次，该电路中的不稳定电容（分布电容、器件的结电容等）都是与该电路并联的，因此适当加大回路电容量，就可以减弱不稳定因素对振荡频率的影响，从而提高了频率稳定度。

最后，当工作频率较高时，甚至可以只利用器件的输入和输出电容作为回路电容。

因而本电路适用于较高的工作频率。

这种电路的缺点是：调C1或C2来改变振荡频率时，反馈系数也将改变。

但只要在L两端并上一个可变电容器，并令C1与C2为固定电容，则在调整频率时，基本不会影响反馈系数。

电容三点式振荡器电路这个电路适合产生几十兆赫以上的信号，常用来作射频振荡器。

第二个图是LC振荡回路的等效电路图，从图上可以看到，电路的振荡频率由L、C、C1、C2决定，基极有一个大电容（1000~2000pF），起交流接地的作用。

由于电感和电容的数值都比较小，所以有些情况下三极管的极间电容、电感线圈的匝间电容都不能忽略。

它们对总电容的贡献量大约几个皮法。

设三极管的极间电容以及电感线圈的匝间电容以及其它分布电容的总等效电容为C0,为了计算方便，选C＝2pF那么电容三点式振荡电路又称考毕兹振荡电路，如图Z0808所示，其结构与电感三点式振荡电路相似，只是将电感、电容互换了位置。

为了形成集电极回路的直流通路，增设了电阻R C。

该电路的交流通路如图Z0809 所示。

可以看出，它符合三点式振荡电路"射同基反"的构成原则，满足自激振荡的相位平衡条件。

在L C谐振回路Q值足够高的条件下，电路的振荡频率为其中这种振荡电路的特点是振荡频率可做得较高，一般可达到100MHz以上，由于C2对高次谐波阻抗小，使反馈电压中的高次谐波成分较小，因而振荡波形较好。

电路的缺点是频率调节不便，这是因为调节电容来改变频率时，（既使C1、C2 采用双连可变电容）C1与C2也难于按比例变化，从而引起电路工作性能的不稳定。

因此，该电路只适宜产生固定频率的振荡。

用集成运放构成的电容三点式振荡电路，如Z0810所示。

可以证明，其振荡频率为：各种振荡器电路的计算器电感三点式振荡器电路图Z0805是电感三点式振荡电路,又称哈特莱振荡电路。

图中L1、L2、C组成谐振回路,L2兼作反馈网络,通过耦合电容C b将L2上反馈电压送到三极管的基极。

由图Z0806交流通路看出,谐振回路有三个端点与三极管的三个电极相连,而且与发射极相接的是L1、L2,与基极相接的是L2、C即满足"射同基反"的原则。

因此电路必然满足相位平衡条件。

5.3.2 三点式振荡电路定义：三点式振荡器是指LC 回路的三个端点与晶体管的三个电极分别连接而组成的反馈型振荡器。

三点式振荡电路用电感耦合或电容耦合代替变压器耦合，可以克服变压器耦合振荡器只适宜于低频振荡的缺点，是一种广泛应用的振荡电路，其工作频率可从几兆赫到几百兆赫。

1、 三点式振荡器的构成原则图5 —20 三点式振荡器的原理图图5 —20是三点式振荡器的原理电路（交流通路）为了便于分析，图中忽略了回路损耗，三个电抗元件be ce bc X X X 、和构成了决定振荡频率的并联谐振回路。

要产生振荡，对谐振网络的要求：？必须满足谐振回路的总电抗0be ce bc X X X ++=，回路呈现纯阻性。

反馈电压f u 作为输入加在晶体管的b 、e 极，输出o u 加在晶体管的c 、e 之间，共射组态为反相放大器，放大器的的输出电压o u 与输入电压i u （即f u ）反相，而反馈电压f u 又是o u 在bc X 、be X 支路中分配在be X 上的电压。

要满足正反馈，必须有()be be f o o be bc ce X X X X X u u u ==-+ （5.3.1）为了满足相位平衡条件，f u 和o u 必须反相，由式（5.3.1）可知必有0be ce X X >成立，即be X 和ce X 必须是同性质电抗，而()bc be ce X X X =-+必为异性电抗。

综上所述，三点式振荡器构成的一般原则：（1） 为满足相位平衡条件，与晶体管发射极相连的两个电抗元件be X 、ce X 必须为同性，而不与发射极相连的电抗元件bcX 的电抗性质与前者相反，概括起来“射同基反”。

此构成原则同样适用于场效应管电路，对应的有“源同栅反”。

（2） 振荡器的振荡频率可利用谐振回路的谐振频率来估算。

若与发射极相连的两个电抗元件be X 、ceX 为容性的，称为电容三点式振荡器，也称为考比兹振荡器(Colpitts)，如图5 —21（a ）所示；若与发射极相连的两个电抗元件be X 、ceX 为感性的，称为电感三点式振荡器，也称为哈特莱振荡器(Hartley)，如图5 —21（b ）所示。