下载文档原格式
MATLAB仿真在光学原理中的应用1. 简介光学是研究光的产生、传播、照明及检测等现象和规律的科学，它在物理学、医学、通信等领域有着重要的应用。
随着计算机科学和数值计算的发展，MATLAB作为一种强大的科学计算软件，被广泛应用于光学原理的仿真和分析中，为光学研究提供了有力的工具和方法。
本文将介绍MATLAB仿真在光学原理中的应用，并通过列举几个典型例子来说明MATLAB在解决光学问题上的优势。
2. 光的传播仿真光的传播是光学研究中的重要内容，MATLAB可以通过数值模拟的方法来进行光的传播仿真。
以下是一些常见的光传播仿真的应用：•光线传播仿真：通过计算光线在不同介质中的折射、反射和衍射等规律，可以模拟光在复杂光学系统中的传播过程。
•光束传输仿真：通过建立传输矩阵或使用波前传输函数等方法，可以模拟光束在光学元件中的传输过程，如透镜、棱镜等。
•光纤传输仿真：通过数值模拟光在光纤中的传播过程，可以分析光纤的传输损耗、模式耦合和色散等问题。
MATLAB提供了许多函数和工具箱，如光学工具箱、光纤工具箱等，可以方便地进行光传播仿真和分析。
3. 光学成像仿真光学成像是光学研究中的重要应用之一，MATLAB可以用于模拟和分析光学成像过程。
以下是一些常见的光学成像仿真的应用：•几何光学成像仿真：根据几何光学理论，可以通过模拟光线的传播和聚焦过程来分析光学成像的特性，如像差、焦距和倍率等。
•衍射光学成像仿真：通过衍射理论和数值计算，可以模拟光的衍射和干涉效应对光学成像的影响，如衍射限制和分辨率等。
•光学投影仿真：通过模拟光束、透镜和光阑等光学元件的组合和调节，可以分析光学投影系统的成像质量和变换特性。
MATLAB提供了丰富的函数和工具箱，如图像处理工具箱、计算光学工具箱等，可以方便地进行光学成像仿真和分析。
4. 激光光学仿真激光是光学研究中的一个重要分支，MATLAB可以用于模拟和分析激光的特性和应用。
以下是一些常见的激光光学仿真的应用：•激光器仿真：通过建立激光器的数学模型和模拟激光的发射过程，可以分析激光器的输出特性和光束质量等。
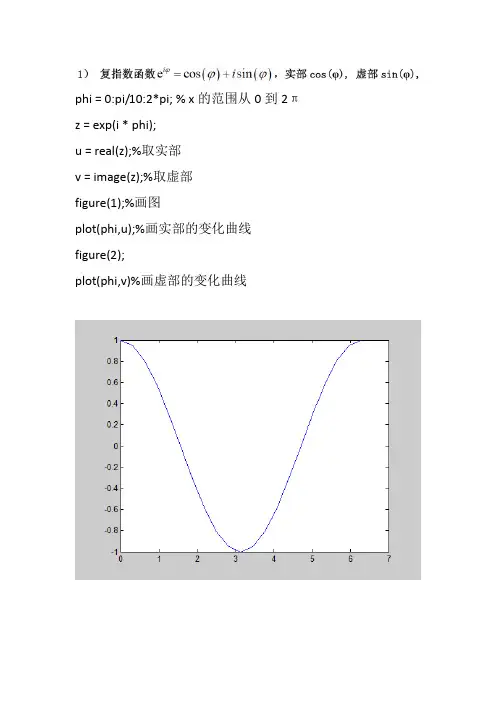
phi = 0:pi/10:2*pi; % x的范围从0到2πz = exp(i * phi);u = real(z);%取实部v = image(z);%取虚部figure(1);%画图plot(phi,u);%画实部的变化曲线figure(2);plot(phi,v)%画虚部的变化曲线clear;%清除内存close all;%关闭所有窗口x=linspace(0,2*pi,100);%设置横坐标范围及网格y1=sqrt(x);%开根号figure(1);plot(x,y1,'r')%做出y1的曲线,'r'代表图线为红色clear;%清除内存close all;%关闭所有窗口x=linspace(-2*pi,2*pi,100);%100个数横坐标从-2pi到2pi y1=besselj(1,x);%第一类贝塞尔函数,一阶y2=besselj(0,x);%第一类贝塞尔函数,0阶figure(1);plot(x,y1,'r');figure(2);plot(x,y2,'b');clear;close all;[x,y]=meshgrid(-2:.05:2,-2:.05:2);%设置二维网格z=sinc(x).*sinc(y);figure(1);imshow(z);%二维灰度图figure(2);imagesc(z);%二维彩图figure(3);mesh(z);%三维图像clear;close all;a=5;x=linspace(-5,5,100);y1=exp(-pi.*(x/a).^2);%第一类贝塞尔函数,一阶b=2;y2=exp(-pi.*(x/b).^2);%第一类贝塞尔函数,一阶figure(1);plot(x,y1,'r');figure(2);plot(x,y2,'b');clear;close all;a=1;b=1;[x,y]=meshgrid(-2:.05:2,-2:.05:2);%设置二维网格z=exp(-pi.*((x/a).^2+(y/b).^2));%高斯函数figure(1);imagesc(z);figure(2);mesh(z);clear;close all;M=100;%x方向抽样点数N=100;%y方向抽样点数w=10;%缝的宽度d=10;%缝偏离中心的位置obj1=zeros(M,N);%赋值为0的一个二维矩阵,大小为M*N obj1(:,(N/2-w/2):N/2+w/2)=1.0;%设置缝在y向中心,且缝的宽度为wfigure(1);imshow(obj1);obj2=zeros(M,N);obj2(:,(N/2-d)-w/2:(N/2-d)+w/2)=1.0;%缝偏离中心位置d个像素figure(2);imshow(obj2);clear;close all;M=100;%x方向抽样点数N=100;%y方向抽样点数w=10;%缝的宽度d=10;%缝偏离中心的位置obj1=zeros(M,N);%赋值为0的一个二维矩阵,大小为M*N obj1(:,(N/2+d)-w/2:(N/2+d)+w/2)=1.0;%设置缝在y向中心,且缝的宽度为wobj2=zeros(M,N);obj2(:,(N/2-d)-w/2:(N/2-d)+w/2)=1.0;%缝偏离中心位置d个像素obj3=obj1+obj2;figure(1);imshow(obj3);clear;close all;M=100;N=100;w=10;%缝宽obj=zeros(M,N);obj((M/2-w/2):(M/2+w/2),(N/2-w/2):(N/2+w/2))=1.0;%缝处于中心位置figure(1);imshow(obj);figure(2);imagesc(obj);figure(3);mesh(obj);。
实验7衍射的Matlab模拟一、实验目的：掌握衍射的matlab模拟。
二、实验内容：1）单个圆孔夫朗和费衍射的matlab模拟2）双圆孔夫朗和费衍射的matlab模拟3）同一波长，狭缝数量分别为1、2、3、6、9、10时候的夫朗和费衍射的matlab模拟4）对4个不同波长的光照射时，狭缝数量分别为1、3时候的夫朗和费衍射的matlab 模拟5）单个圆孔菲涅尔衍射的matlab模拟6）模拟圆孔（或者单缝）衍射时，衍射屏到接收屏距离不同的时候衍射的图样1)clearclclam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;hh=(2*BESSELJ(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;B=b/max(b);endimage(xs,ys,b);colormap(gray(n));figure;plot(xs,B);colormap(green);-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-3-3-2-10123x 10-300.10.20.30.40.50.60.70.80.912)%双圆孔夫琅禾费衍射clear all close all clc %lam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:m r=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;h=(2*BESSELJ(1,x)).^2./x.^2;d=10*a;deltaphi=2*pi*d*xs(i)/lam;hh=4*h*(cos(deltaphi/2))^2;b(:,i)=(hh)'.*5000;end image(xs,ys,b);colormap(gray(n));-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-33)lamda=500e-9;%波长N=[1236910];for j=1:6a=2e-4;D=5;d=5*a;ym=2*lamda*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(j)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure(j);subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);plot(B1,ys,'k');end-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为2-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为3-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为9狭缝数为6-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.0254）lamda=400e-9:100e-9:700e-9;%波长N=[13];a=2e-4;D=5;d=5*a;for j=1:4ym=2*lamda(j)*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for k=1:2for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda(j);beta=pi*d*sinphi/lamda(j);B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(k)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);狭缝数为10plot(B1,ys,'k');end end-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02Lamda=400nm,N=1-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025Lamda=400nm,N=3Lamda=500nm,N=1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03Lamda=500nm,N=3Lamda=600nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04Lamda=600nm,N=3Lamda=700nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.045）clearclcN=300;r=15;a=1;b=1;I=zeros(N,N);[m,n]=meshgrid(linspace(-N/2,N/2-1,N));D=((m-a).^2+(n-b).^2).^(1/2);i=find(D<=r);I(i)=1;subplot(2,2,1);imagesc(I)colormap([000;111])axis imagetitle('衍射前的图样')L=300;M=300;[x,y]=meshgrid(linspace(-L/2,L/2,M));lamda=632.8e-6;k=2*pi/lamda;z=1000000;Lamda=700nm,N=3h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z); H=fftshift(fft2(h));%传递函数B=fftshift(fft2(I));%圆孔频谱G=H.*B;U=fftshift(ifft2(G));Br=(U/max(U));subplot(2,2,2);imshow(abs(U));axis image;colormap(hot)%figure,imshow(C);title('衍射后的图样');subplot(2,2,3);mesh(x,y,abs(U));subplot(2,2,4);plot(abs(Br))6)lamda=500e-9;%波长N=1;%缝数，可以随意更改变换a=2e-4;D=3:7;d=5*a;for j=1:5ym=2*lamda*D(j)/a;xs=ym;%屏幕上y的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:nsinphi=ys(i)/D(j);alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);endNC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1)image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2)plot(B1,ys,'k');end-0.4-0.200.20.4-0.015-0.01-0.00500.0050.010.01500.51-0.015-0.01-0.0050.0050.010.015D=3m-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025D=5m D=4m-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04D=7m D=6m。
《基于Matlab的光学实验仿真》篇一一、引言光学实验是研究光学现象和规律的重要手段，但在实际操作中往往受到诸多因素的限制，如实验设备的精度、实验环境的稳定性等。
因此，通过计算机仿真进行光学实验具有很大的实际意义。
本文将介绍一种基于Matlab的光学实验仿真方法，以期为光学研究提供一定的参考。
二、仿真原理及模型建立1. 仿真原理基于Matlab的光学实验仿真主要利用了光学的基本原理和数学模型。
通过建立光学系统的数学模型，模拟光在介质中的传播、反射、折射等过程，从而实现对光学实验的仿真。
2. 模型建立在建立光学实验仿真模型时，需要根据具体的实验内容和目的，选择合适的数学模型。
例如，对于透镜成像实验，可以建立光学系统的几何模型和物理模型，通过计算光线的传播路径和透镜的焦距等参数，模拟透镜成像的过程。
三、Matlab仿真实现1. 环境准备在Matlab中，需要安装相应的光学仿真工具箱，如Optic Toolbox等。
此外，还需要准备相关的仿真参数和初始数据。
2. 仿真代码实现根据建立的数学模型，编写Matlab仿真代码。
在代码中，需要定义光学系统的各个组成部分（如光源、透镜、光屏等），并设置相应的参数（如光源的发光强度、透镜的焦距等）。
然后，通过计算光线的传播路径和光强分布等参数，模拟光学实验的过程。
3. 结果分析仿真完成后，可以通过Matlab的图形处理功能，将仿真结果以图像或图表的形式展示出来。
通过对仿真结果的分析，可以得出实验结论和规律。
四、实验案例分析以透镜成像实验为例，介绍基于Matlab的光学实验仿真方法。
首先，建立透镜成像的数学模型，包括光线的传播路径和透镜的焦距等参数。
然后，编写Matlab仿真代码，模拟透镜成像的过程。
最后，通过分析仿真结果，得出透镜成像的规律和特点。
五、结论与展望基于Matlab的光学实验仿真方法具有操作简便、精度高等优点，可以有效地弥补实际实验中的不足。
通过仿真实验，可以更加深入地了解光学现象和规律，为光学研究提供一定的参考。
2007级计算机课程设计测控与光电技术学院电子科学与技术专业课程设计题目圆孔衍射现象计算机仿真设计学生姓名吴海班级070832指导教师钟可君日期2010 年6 月28 日南昌航空大学测试与光电工程学院计算机课程设计任务书电子科学与技术系070832 班学生：吴海课题名称：圆孔衍射现象计算机仿真设计课题内容：1、课题设计要求：(1)分析圆孔衍射的物理过程，建立数学模型；(2)设计算法流程图；(3)编写程序，并对仿真结果进行分析。
2、工作进度安排：查阅资料，设计算法流程图6月28日～7月4日第18周编写程序，撰写报告7月5日～7月9日第19周主要参考资料：[1]. 姚启钧.光学教程[M]. 北京：高等教育出版社[2]. 宋清，熊万杰.光学现象的计算机仿真[J].中山大学学报论丛，2005，25（3）：24-29.[3].圆孔衍射与像分辨本领的MATLABF仿真分析[J].湖北工学院学报，2004，19（5）：47-49.[4].MATLAB GUI在光学仿真中的应用[J].通化师范学院学报，2010,31（2）：52-54.系负责人：指导教师：钟可君时间：2010年6月21日单孔衍射上机试验上机试验程序（1）%圆孔衍射clcclearlam=500e-9a=1e-3f=1m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lamhh=(2*BESSELJ(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;endsubplot(1,2,1)image(xs,ys,b)colormap(gray(n))subplot(1,2,2)b(:,m/2)plot(ys,b(:,m/2))程序运行后的结果单孔衍射图光强分布图[摘要]运用MATLAB6的软件平台,编制演示程序,对圆孔衍射像分辨本领进行仿真分析.[关键词]圆孔衍射;分辨本领; Airy斑;仿真分析意义：圆孔作为光学仪器基本形状,其衍射现象在光学研究中占有重要地位.光学衍射现象的实验演示需要特定的实验仪器和实验所,给研究工作带来许多不便.另外,清晰的圆孔衍射图样,要求的圆孔半径很小,在一般实验中难以实现.基于MATLAB6软件强大的计算能力和可视化功能上的优势,利用计算机对圆孔衍射过程进行仿分析,可以使衍射现象直观地表现出来;通过调整实验参数,可以同步生成不同实验条件下的衍射图样,便于对衍射现象和像分辨本领进行比较分析;利用色图表现光强分布,使实验效果更为逼真,在实和研究中具有重要意义.1圆孔衍射的实验装置与数学模型的、建立圆孔夫琅禾费衍射装置如图1所示,S为点光源,位于透镜L1的焦平面的主光轴上,光屏E置于焦距为D的透镜L2的焦平面上.圆孔P的半径为R.入射光波长为λ.射圆孔时,沿衍射角θ方向传播的次波在光屏Q(x,y)处的光强分布为[1]Iθ= I0(J1(2m)m)2.其中:m=πRλsinθ,sinθ=x2+y2x2+y2+D2;I0为分常数.2主程序编写与衍射图样的生成运用MATLAB编制运算程序circle_aperturebase01.m,程序运行后,在坐标区可以生成圆孔琅禾费衍射图样.为了满足程序的普遍性和通用性,主程序中共设置5个输入参数,分别为λ,D,R,θ0(入射光垂直入射为θ0=0),最大坐标范围xmax.长度以毫米为单位.主程序circle_aperture_base01.m如下:function circle_aperture_base01(lambda,D,R,theta0,xmax) %对参量赋值lambda=6.328*1e-4;D=64;R=0.02;xmax=pi;theta0=0%设定图像的范围,并把x分成401个点(根据程序需要,设为奇数点).x=linspace(-xmax,xmax,401);[x,y]=meshgrid(x); %%建立x,y网格%建立强度分布矩阵x0=D*tan(theta0);sin_theta=sqrt(((x-x0).^2+y.^2)./((x-x0).^2+y.^2+D^2)); %%sin(theta)z=R*sin_theta/lambda; %%z=Rsin(theta)/lambdam=pi*z;I=(bessel(1,2*m)./m).^2;%生成强度分布图%绘制相对光强与x坐标的关系曲线(沿y=0方向) subplot('position',[0.15 0.6 0.7 0.35]),plot(x(1,:),I((end+1)/ 2,:))%绘制相对光强与坐标(R*sin(theta)/lambda)的关系曲线(沿y=0方向)subplot(2,2,3),plot(z((end+1)/2,:),I((end+1)/2,:));%绘制强度分布的灰度图NCLevers=255; %%确定用的灰度等级为255Imax=max(max(I));Ir=I/Imax*NCLevers;colormap(gray(NCLevers)); %%用灰度级颜色绘图subplot(2,2,4),image(x(1,:),y(:,1),Ir) %%绘制强度的灰度图axis squareaxis([-2 2 -2 2]);colorbar('vert')程序运行后,在坐标区,生成强度分布曲线和色图(如图2,图中的极值判断和文字标示命令在程序中未列出).图中,上图表示强度沿x坐标(y =0)分布,下图左侧表示强度随无量纲因子Rsinθ/λ的变化规律,右侧则表示光强在xoy平面的变化规律,中央的白色亮区为Airy斑.在光强曲线图中,用红点和绿点表示极大值点和极小值点,对应坐标也在图2(c)中央明区中给出.3衍射图样分析3.1Airy斑与极小值由图2可知,当Rsinθ/λ≈0.61时,出现第一级极小值.定义在光屏上由两个第一级极小值之间所围圆形区间为Airy斑.Airy斑的中心位于坐标原点,其角半径为0.61λ/R,如图所示.3.2第一级次极大由图2可知,当Rsinθ/λ≈0.82时,出现第一级次极大值,其相对光强为1.7%.其余次极大的光强将更小.3.3参数对衍射图样的影响进一步调整参数R、D及λ,其Airy斑及各级衍射环的相对位置发生变化.如图3所示,Airy斑的角半径与R成反比,与λ成正比,其线半径与D成正比.5结论从上面的一系列讨论可以发现,通过计算机编程,对圆孔夫琅禾费衍射进行仿真分析,无需复杂的实验仪器和苛刻的实验环境,可在短时间内完成多种实验条件衍射图样的演示.运用MATLAB强大的数值计算功能和优越的可视化特征,可以同步求出衍射图样的一些重要物理量的数值,满足仿真实验的需要,为教学和研究工作提供了强有力的演示工具.利用计算机编程,仿真演示复杂的物理现象, 作为计算物理学的一个发展方向,具有广阔的发展前景.[参考文献][1]姚启钧.光学教程[M].北京:高等教育出版社, 2002.[2]赵凯华,钟锡华.光学(上册)[M].北京:北京大学出版社, 1984.摘要:采用matlab7.0强大的函数作图功能对圆孔、矩孔和双矩孔的夫琅和费衍射进行模拟,建立直观形象并且精确完整的理论模型,并附上程序代码,将干涉理论联系起来,分析衍射和干涉的本质。
西安工业大学毕业设计(论文)开题报告题目：基于Matlab的光学衍射实验仿真系别光电信息系专业光电信息工程班级XXX姓名王XX学号X070104XX导师XX2010 年11 月27 日课题背景及研究意义衍射是光波的一种重要特征,对光波衍射现象的讨论是以惠更斯- 菲涅尔原理为基础的。
事实证明，在大多数光学问题中，可以采用光场的标量衍射理论来描述和计算。
光场的频率非常高，只能测量在一个比光的周期大得多的时间间隔内的平均值，在计算衍射光波场的光振动和光强分布时则利用菲涅尔- 基尔霍夫衍射积分公式[1,2,3]。
在物理光学的光的衍射教学过程中，光学实验内容比较抽象, 如不借助实验, 学生很难理解理论、实验原理和过程。
通常，学校的教学中，将光学理论教学与实验教学相分离，理论教学中需要实验现象来验证，而光学实验的进行一般要稳定的环境、高精密的仪器, 复杂的实验仪器以及光路的调试, 花费了技术人员相当多的时间，往往很难调试到理想的状态，搭建好的仪器和光路也会受到环境和温度的影响,有时实验结果将偏离理论预测。
为了在物理光学课程教学过程形象生动，需要现代化的教学手段，千方百计地为学生提供观察物理现象的机会，提高学生学习光学课程的兴趣，培养他们的思维水平和创新能力，应该充分利用计算机软件功能为教学增添活力，为学生理解复杂理论和实验做好铺垫，可以用MATLAB软件为平台,对光学实验进行计算机仿真，具有两个方面意义：一方面，利用仿真结果指导实际实验。
前期投资少，且可以减少贵重仪器的损伤等；另一方面，在教学上，将抽象难懂的概念、规律通过实验仿真生动、形象地表现出来，使学生更易于接受，具有明显的教学效果。
还可以鼓励学生自主探索，研究一些更深入的光学问题，这样可以拓宽知识面，提高能力[4,5,6]。
国内外研究情况在用计算机模拟[7]光学实验软件方面，国外的光学衍射模拟试验是在模拟设计和优化光学系统的过程中发展起来的。
在这方面，美国走在最前面，他们最具代表性的是劳伦斯利弗莫尔实验室光传输模拟计算软件Prop92[8,9]及大型总体优化设计软件CHAINOP 和PROPSUITE[10]。
光的干涉和衍射的matlab模拟单缝夫琅和费衍射是光的衍射现象之一，如图2所示。
当单色光波通过一个狭缝时，光波会向周围扩散，形成一系列同心圆环。
这些圆环的亮度分布是由夫琅和费衍射公式描述的，即。
其中为入射光波长，为狭缝宽度，为衍射角。
夫琅和费衍射公式表明，随着衍射角的增大，圆环的半径会减小，而亮度则会逐渐减弱。
在MATLAB中，可以通过输入实验参数，如光波长和狭缝宽度，来观察圆环的亮度分布和半径随衍射角的变化情况。
同时，还可以探讨不同波长和狭缝宽度对圆环亮度和半径的影响。
4双缝衍射双缝衍射是光的干涉和衍射现象的结合，如图3所示。
当一束单色光波通过两个狭缝时，光波会在屏幕上形成一系列干涉条纹和衍射环。
干涉条纹的亮度分布与___双缝干涉相同，而衍射环的亮度分布则由夫琅和费衍射公式描述。
在MATLAB中，可以通过输入实验参数，如光波长、双缝间距和双缝宽度，来观察干涉条纹和衍射环的亮度分布和条纹间距、环半径随实验参数的变化情况。
同时，还可以探讨不同实验参数对干涉条纹和衍射环的影响。
5衍射光栅衍射光栅是一种利用衍射现象制成的光学元件，如图4所示。
当一束单色光波通过光栅时，光波会被分为多个衍射光束，形成一系列亮度不同的衍射条纹。
衍射条纹的亮度分布与夫琅和费衍射公式描述的圆环类似，但是条纹间距和亮度分布会受到光栅常数的影响。
在MATLAB中，可以通过输入实验参数，如光波长和光栅常数，来观察衍射条纹的亮度分布和条纹间距随实验参数的变化情况。
同时，还可以探讨不同实验参数对衍射条纹的影响。
总之，通过MATLAB模拟光的干涉和衍射现象，可以更加直观地理解和掌握这些重要的光学现象，同时也可以为实验设计和数据分析提供有力的工具和支持。
本文介绍了___双缝干涉、单缝夫琅禾费衍射和衍射光栅光谱的计算机模拟。
当一束单色平行光通过宽度可调的狭缝，射到其后的光屏上时，形成一系列亮暗相间的条纹。
单缝夫琅禾费衍射的光强分布可以通过惠更斯-费涅耳原理计算。
MATLAB编程用两种方法模拟光学实验03级物理一班李超PB03203017摘要：利用MATLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟；以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。
关键词：MATLAB；衍射积分；傅立叶变换；计算机模拟引言：美国Mathworks公司推出的MA TLAB，是一种集数值计算、符号预算、可视化建模、仿真和图形处理等多种功能于一体的优秀图形化软件。
本文介绍了通过MA TLAB软件编程实现用衍射积分和傅立叶变换实现夫琅和费衍射计算机模拟的方法。
计算机模拟为衍射实验的验证提供一条简捷、直观的途径。
从而加深了对物理原理、概念和图像的理解。
正文：大学教学课程中引入计算机模拟技术正日益受到重视，与Basic、C和Fortran相比，用MA TLAB软件做光学试验的模拟，只需要用数学方式表达和描述，省去了大量繁琐的编程过程。
下面来介绍利用MATLAB进行光学模拟的两种方法。
（一）衍射积分方法：该方法首先是由衍射积分算出接收屏上的光强分布，然后根据该分布调制色彩作图，从而得到衍射图案。
1．单缝衍射。
把单缝看作是np个分立的相干光源，屏幕上任意一点复振幅为np个光源照射结果的合成，对每个光源，光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2，其中α=2Δ/λ=πypys/λD编写程序如下，得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1) image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2． 杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π（r 2-r 1）/λ,光强I=4I 0cos 2（Φ/2） 编写程序如下，得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2); r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); end N=255;Br=(B/4.0)*Nsubplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3． 光栅衍射公式：I=I 0（sin α/α）2（sin(λβ)/sin β）2α=(πa/λ)sin Φ β=(πd/λ)sin Φ编写程序如下：得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);图2 杨氏双缝干涉的光强分布 图3 黑白光栅衍射光强分布end NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);（二）傅立叶变换方法：在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。
利用MATLAB语言进行光学衍射现象的仿真储林华（安庆师范学院物理与电气工程学院安徽安庆246011）指导教师：张杰摘要：光的衍射是光的波动性的一种重要表现，因此对光的衍射现象的研究，不仅具有重要的理论意义，而且在光学仪器研制和成像分析等诸多实际应用方面均有重要价值，但是其衍射光强的计算非常复杂，对实验条件的要求非常高，通常情况下很难得到满意的效果，严重影响了光学的教学。
本文从衍射的相关理论知识出发，首先介绍了惠更斯--菲涅耳原理及其数学表示形式，然后重点讨论了单色光经各种对称光学衍射元件（单缝，双缝，光栅，圆孔）的夫琅和费衍射情况，并分别给出了它们在焦平面上的衍射光强计算公式，最后利用科学计算软件MA TLAB对光的衍射现象进行了仿真，所得到的图样细致逼真，使整个物理过程变得直观形象，且与实验所得到的衍射图样进行了比较，两者吻合得很好，从而为光学的理论分析和实验教学提供了一种新的途径。
关键词：光的衍射，光栅衍射，圆孔衍射，Matlab，计算机仿真0 引言光的衍射现象是光具有波动性的重要特征，因此对衍射现象的研究无论在理论上还是在实践中都有很重要的意义。
对光的衍射现象的研究，始于17世纪，当时著名的荷兰科学家惠更斯提出了光是一种波的假说，并根据波动理论提出了光的传播理论——即惠更斯原理[1]，根据这一原理，他解释了光的反射定律和折射定律，给出了折射率的意义，光在两种介质中的速度比。
到了19世纪，法国年轻的科学家菲涅耳，根据叠加原理把惠更斯原理进一步具体化，给出了光在传播过程中光强学计算公式，这就是著名的惠更斯-菲涅耳原理[2]。
但由于在实际应用过程中，障碍物形状的不规则性，导致光强的计算公式几乎无解析解，只能进行一些数值计算。
针对衍射计算中出现的困难，近代的研究人员想到运用科学的计算软件MA TLAB，利用其较强的绘图和图象功能，编写计算程序，使得多种衍射元件（单缝，双缝，光栅，矩孔，圆孔）下的衍射现象得以在计算机中形象地被模拟仿真。
这种做法，条件限制较少，对于衍射的实验教学是一种的补充，起到了很不错的效果；但值得指出的是，许多前人撰写的论文，总是在系统化，可视化，条理化方面不够理想，本文将在他们工作的基础上，将此课题进一步做得完美。
1．惠更斯—菲涅耳原理早在十七世纪后期，荷兰科学家惠更斯就提出了光是一种波动的假说，并阐述了关于波面传播的一种理论，既惠更斯原理。
该原理认为，传播中的波面上任何一点都可以认为是一个新的次波源，由于这些次波源发出的次波是球面波，这些次波的公共包络面就是下一时刻的波面，根据这一原理，他解释了光的反射定律和折射定律，并给出了折射率的意义，光在两种介质中的速度比。
菲涅耳根据叠加原理把惠更斯原理进一步具体化了，他假设各次波是球面波，但这些球面只是等相面而不是等幅面，球面上各点振幅与传播方向有关，这就避免了次波的后向的传播；同时，他认为，下一时刻空间任一点的振动由各次波到达该点的振动叠加所决定，此定理称为惠更斯—菲涅耳定理。
如右图（1）所示。
菲涅耳假设：Q 点所发的次波对P 点贡献dU(p)正比于Q 点附近一个小面元的面积ds ， 正比于Q 点的复振幅U(Q)，正比于e jkr /r (假定次波是球面波)，以及正比于一个与传播方向有关的函数f(θ)(θ是r 与小面元法线即波在Q 点的传播方向上的夹角)，即：()()()jkru Q f e du p c ds rθ=其中C 是一个与r ，Q ，θ无关的比例系数，f(θ)叫倾斜因子，它随θ增加而缓慢减少于是，按照叠加原理，有：()()()()jkrssu Q f u p du p ce ds rθ==⎰⎰ （1） 这就是惠更斯—菲涅耳原理的数学表达式，积分表示整个波面S 上各点所发的次波传播到P 点的作用的叠加。
从上面的表述，我们可以看到菲涅耳的思想比惠更斯有了更大的进步，他着眼于下一时刻空间各点的振动情况，而惠更斯只着眼于下一时刻波面的形状与位置，因此惠更斯只能定性地描述光的传播方向，而菲涅耳却能定量地描述衍射后的光强分布。
2. 夫朗禾费衍射现象研究光的衍射现象根据光源到衍射屏以及观察屏的距离远近，可以分为近场衍射和远场衍射。
如果光源到衍射屏以及观察屏的距离为有限值，则称为近场衍射（菲涅耳衍射）；如果光源到衍射屏以及观察屏的距离为无穷远，则称远场衍射，由于这种衍射最先由夫朗禾费在探索天体成像时作了系统的研究，故亦称为夫朗禾费衍射。
一般情况下，利用（1）式进行光强计算时，菲涅耳衍射情况比较复杂，而夫朗禾费衍射情况比较简单,本文仅讨论后者。
2.1 圆孔的夫朗禾费衍射在Oxy 平面上，有一以O 为圆心、R 为半径的圆孔，如图2所示。
现用一束平行于Z 轴的光线照射,经圆孔衍射后到达焦平面上，于是按照（1）式，P 点的光强为：()()()Qjkr QQu Q f u p ce ds r θ=⎰圆孔20()()QRjkr Qu Q f ce d d r πρψθρρψ===⎰⎰ 图1 波面上各点复振幅的传播图2 圆孔衍射示意图(a)(b)设从圆心O 到P 点的距离为r 0，则从圆孔中任一点Q 到P 点的距离r Q 为：'00sin cos sin Q r r oo r θρϕθ=+=+于是,由于程差0Q r r ∆=-比0r 小得多，而与波长λ可以比拟，因此，可以把振幅中的Q r 以0r 代替而只考虑相位因子的变化，即：02()'00()Q R jk r r u p ced d πρρψ-=⎰⎰ （2）其中：0'()()jkr u Q f c ce r θ=为常数，将r Q 代入（2）式中得： 2'cos sin '21002()()R jk J x u p c e d d c R x πρψθρρψπ⎡⎤==⎢⎥⎢⎥⎰⎰其中：1J 称为一阶贝塞尔函数，2sin x R πθλ=，由此，可知P 点的光强可表达为：22'22412()()()J x I p u p c R x π⎡⎤==⎢⎥⎣⎦（3） 根据(3)式可以画出焦平面的光强分布图样，如下图(3)所示：(a) (b)图3 圆孔衍射图样其中，图（b ）是夫朗禾费衍射图样的照片。
显然，这是一个圆对称图形，中心为主极大，在F 处，0000,x I I θ====’R ，，，其他各点的光强可通过 'R 来表示，由图(2)可知：'''sin 2xf R f Rλθπ== 当：''00.61 1.22,0,f R x I I R λπ===时， 为第一暗环；''0.8180.0175,f R R λπ==0时，x=1.635,I I 为第一亮环；''01.116 2.233,0,f R x I I R λπ===时， 为第二暗环；''01.619 3.238,0f R x I I R λπ===时，， 为第三暗环。
这就是夫朗禾费圆孔衍射的光强分布，它的中心永远是亮的，并且在中心亮斑处的光能占总光能的约84%，中心亮斑的半径也是确定的，为'f R λ0.61，或角半径为0.61R λ。
2.2 单缝的夫朗禾费衍射图4 单缝夫朗禾费衍射示意图设波长为λ的平面波射向缝宽AB=b 的狭缝，衍射经透镜L 会聚在焦平面F 上，取XZ 坐标如图(4)所示，根据惠—菲原理，在焦平面上任一点P 的复振幅为：()()()jkru Q f u p ce ds rθ=⎰狭缝把狭缝细分为垂直于X 轴的许多小面元，面积为ds=Ldx ，L 是缝的长度，由于是平面波入射，故U （Q ）为常数，在角度不大的情况下，0()1,sin f r r x θθ≈=+，由于0x r <<，故在振幅中的r 可视为0r ，只有相位因子中的0sin r r x θ∆=-=不可略去，故：2sin 02()()b jkr jkx b e u p cLu Q e dx r θ-=⎰把积分求出，得：'sin sin '222()()sin(sin )sin sin 2b b jk jkc b cu p eek jk k θθθθθ-=-=令： sin sin 2bb kπθθβλ== 则：'sin ()u p c b ββ=2'222220()()sinsin I u p u p c b I ββββ*=== (4)其中，0I 为0β=时的光强，即：衍射斑中心点的光强，β的物理意义是狭缝的边缘与中心的光线在P 点产生的相位差，以β或sin θ作横坐标，以0I I 作纵坐标，对(4)式作图可得夫朗禾费单缝衍射的光强分布，如下图所示：（a ）单缝衍射的光强分布-20-15-10-5510152000.20.40.60.81(b)单缝衍射图样图5 单缝衍射光强分布及图样计算表明，在 πβπ-<<之间的主极大集中了90%的能量，主极大的半角宽为sin b θθλ≈=，把狭缝改为矩孔，即在x ，y 两个方向上考虑衍射效应，则光强表达式为：22220sin sin I I ββαα= 其中，α是在y 方向上与β对应的量，矩孔衍射图样如图(6)所示，图6 矩孔衍射图样2.3 双缝的夫朗禾费衍射以上考虑的是一个缝的衍射，如果有两个相邻的缝，由于衍射，通过两个缝的光在观察屏上会相遇。
试验结果告诉我们，在两条缝的衍射光相互交叠的区域，不是简单的呈现光强的叠加，而是出现了由光强重新分布而产生的明暗相间的条纹，称为光的干涉。
显然，光的干涉与光的衍射一样，都是波的叠加原理所必然导致的结果。
现在，我们仍然用惠—菲原理来分析两条缝所产生的夫朗禾费衍射的结果，如图(7)所示：图7 双缝衍射示意图如图(7)，衍射屏上A ，B 处各有一条宽为b 的缝，缝间距为d ， 由于透镜的作用，这两条缝的衍射光在焦平面F 上的光强分布是完全一样的，但它们的相位分布不同，把坐标原点分别放在A 与B 的中心，由式： 2'sin 2()b jkx b u p ce dx θ-=⎰可得：2()sin '22()A b djk x A A b u p c edx θ+-=⎰2()sin '22()B b djk x B B b u p cedx θ--=⎰令：sin 2dr kθ=为单缝中心与双缝中心的光在P 点产生的相位差，则：2'sin 2()()()()b jkx jr jr A B b u p u p u P C e dx e e θ--=+=+⎰='sin ()jrjrc b e e ββ--+于是，总光强为：220()()sin ()()jr jr jr jr I u p u p I e e e e ββ*--==++=22204sin cos I r ββ （5）这就是夫朗禾费双缝衍射的光强分布的表达式，设d=5b ， 即：r=5β，将式(5)作图，可得下图所示的光强分布图样：1234图8 双缝衍射光强分布图样显然，这是由22sin ββ与24cos r 相乘而得的图样，在有双缝时，原来的单缝衍射图形不是平均地增加到原来的两倍，而是在sin k d θλ=时，增加到原来的四倍，在sin (21)/2k d θλ=+处，降为零。
