下载文档原格式
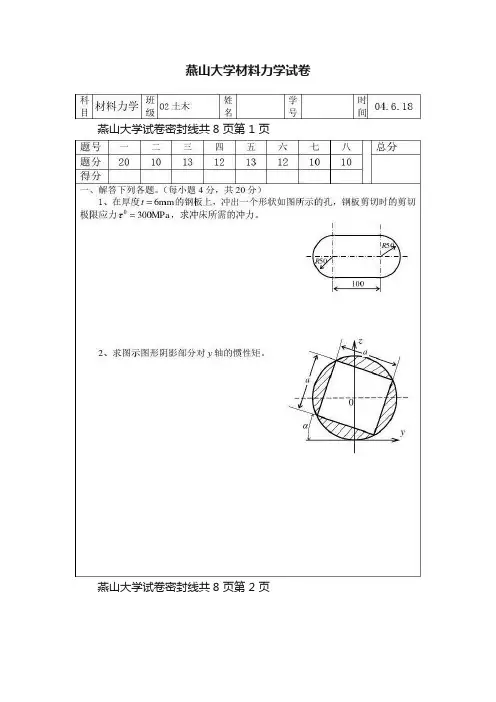
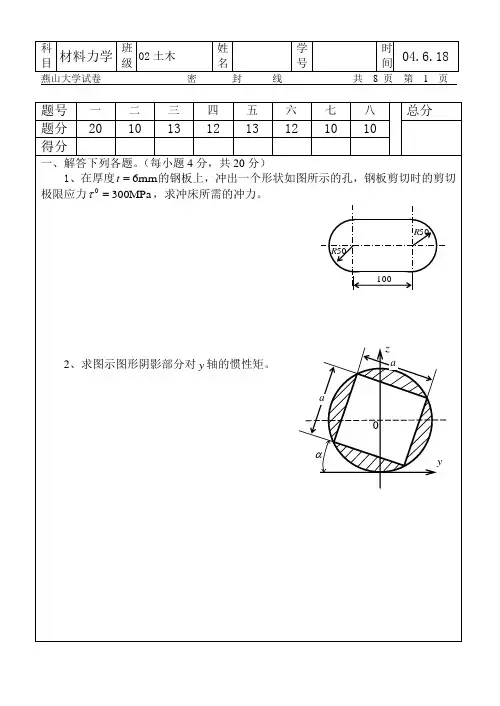
1、变形固体的基本假设。
内力、截面法。
应力、应变、虎克定律。
杆件的基本变形形式。
2、轴向拉伸和压缩的概念和实例。
横截面上的内力和应力。
材料在拉伸与压缩时的力学性能。
许用应力、强度条件。
拉伸和压缩时的变形。
拉压静不定问题。
温度应力。
装配应力。
3、剪切和挤压的实用计算。
4、外力偶矩与扭矩的计算。
薄壁圆筒的扭转、纯剪切。
圆轴扭转时的应力和变形。
圆轴扭转的强度和刚度计算。
5、静矩和形心。
惯性矩、惯性积、惯性半径。
平行移轴公式。
转轴公式。
主惯性轴、主惯性矩。
6、剪力与弯矩。
剪力与弯矩方程。
应用内力方程作剪力图与弯矩图。
载荷集度、剪力和弯矩间的微分关系。
应用微分关系作剪力图和弯矩图。
叠加法作弯矩图的概念。
7、弯曲正应力。
弯曲切应力。
弯曲正应力和切应力强度计算。
弯曲中心。
8、挠度和转角。
梁的刚度条件。
挠曲线的近似微分方程。
积分法求梁的变形。
叠加法求梁的变形。
9、一点应力状态的概念。
平面应力状态分析的解析法和图解法。
三向应力状态简介。
平面应变状态分析。
广义虎克定律。
10、组合变形的概念。
斜弯曲。
拉伸或压缩与弯曲的组合。
偏心压缩（拉伸）、截面核心。
强度理论的概念。
四种常用的强度理论。
扭转和弯曲的组合。
11、结构变形能的计算。
单位载荷法。
图形互乘法。
功的互等定理。
12、静不定系统的概念。
力法解静不定问题。
对称及反对称性质的应用。
静不定结构的位移。
13、动静法的应用。
构件受冲击时的应力和变形。
14、压杆稳定的概念。
两端铰支细长压杆的临界力。
不同杆端约束细长压杆的临界力。
欧拉公式的适用范围、经验公式。
临界应力总图。
压杆稳定性计算的安全系数法。
2008年硕士研究生入学考试初试试题科目代码: 816科目名称: 理论力学共1页请将试题做在标准答题纸上，在题签上做题无效。
本试题应使用计算器。
一、图示平面结构中,各杆自重不计。
已知P = 20kN, M = 10kN.m, q = 4kN/m,尺寸如图。
求支座A和D处的约束力。
(30分)二、平面曲柄连杆滑块机构中，0A=I，曲柄0A上作用有矩为M的力偶，0A水平,A、B处为铰接。
连杆AB与铅垂线夹角为日,滑块与水平面间摩擦系数为f,不计各构件自重，且tanθ>f。
求机构保持平衡时水平力F的最小值。
(18分)三、弯成直角的曲柄OAB以匀角速度w绕0轴转动，AO=r。
在曲杆的AB段装有滑筒C,滑简又与铅直杆DC铰接,0点与DC位于同一铅垂线上。
求当φ= 30°时DC杆的速度和加速度。
(26分)四、图示机构中，杆AB以匀角速度w绕A轴转动，尺寸和位置如图所示。
求此.时C点的加速度。
(26 分)五、图示机构中,沿斜面纯滚动的國柱体0和滚轮0为均质物体,质量均为m,半径均为R,不计绳重和伸长，斜面倾角为日,鼓轮0上作用一力偶矩为M的常力偶。
求鼓轮0的角加速度和轴承0处的约束力。
(30 分)六、图示机构中,两均质杆AB和OB的质量均为m,长度均为I,初始时AB⊥0B,并由静止开始在铅垂面内倒下，不计各处摩擦。
求两杆下落到水平面时OB杆的角速度。
(20分)2009年项士研究生入学者试初试试题科目代码: 815科目名称:理论力学一(20 分)图示构架，由直杆BC、CD及直角弯杆AB组成，各杆自重不计，载荷分布及尺寸如图所示。
销钉B穿透AB及BC两构件，在销钉B上作用一集中载荷P。
已知q、a、M且M = 2qa2。
求固定端A的约束反力及销钉B对BC杆、AB杆的作用力。
二、(10分)图示六根杆支承一个水平板，在板角处受铅垂力作用。
设板和杆自重不计，求各杆的内力。
三(20分)均质圆柱重P、半径为r，搁在不计自重的水平杆和固定斜面之间。
