下载文档原格式
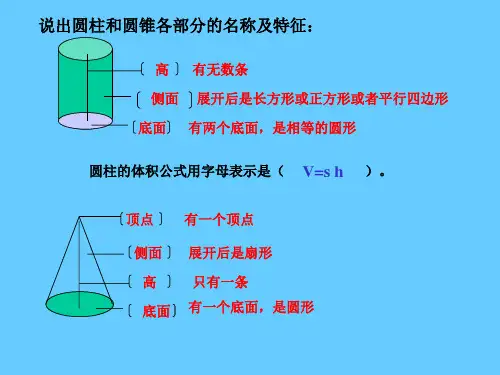
圆锥体的体积公式推导
圆锥体是一种常见的几何体，它由一个圆锥面和一个封闭底面圆共同构成，其中底面圆的面积为S，圆锥高为h。
推导圆锥体的体积公式需要运用积分学的知识。
假设圆锥体在z轴上，底面圆的圆心在原点，半径为r。
将圆锥体分成无数个薄片，每一层的厚度为dz，圆锥面积为A(z)。
则某一层的体积为 dV = A(z) * dz。
由于圆锥面积和高成比例，可得 A(z) = πr(z/h)，代入上式得dV = πr(z/h) * dz。
将所有层的体积累加，得到整个圆锥体的体积公式为：
V = ∫[0,h] πr(z/h) dz = 1/3πrh
其中∫[0,h]表示对z从0到h积分，r为底面圆的半径，h为圆锥高。
故圆锥体的体积公式为1/3πrh。
- 1 -。
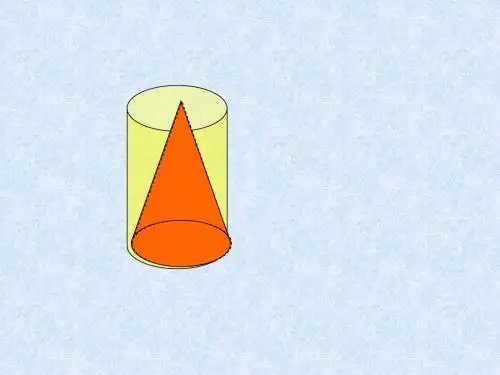
圆锥的体积公式推导
两方面，一方面介绍圆锥面方程，另一方面介绍圆锥的体积公式推导。
一：圆锥面方程为()2222y x a z +=，R
h a ==αcot （α为圆锥的半顶角，h 为圆锥的高，R 为圆锥的地面半径） 圆锥面可看成一条过原点的直线以倾角απ-，绕原点旋转形成。
现取xoz 平面，则该直线的解析式为
αcot x z =
可得该圆锥面方程为：
α
c o t 22y x z +±= 两边平方，并令a =αcot ，则上式可改写为：
()2222y x a z +=
此为定点在原点的圆锥面方程。
二：圆锥体积公式推导
注意到圆锥面在xoy 平面上的投影为半径为R 的圆。
设所形成的投影的体积为V
则：
222:R y x D z d x d y V D ≤+=⎰⎰
代入，可得：
d x d y
y x a V D ⎰⎰+=22 令
θc o s r x =，θsin r y =
[][]πθ2,0,,0∈∈R r
则：
dr r d V R ⎰⎰=
0220πθ 33
2R a π=
h R 23
2π= 圆锥面所形成的的投影的体积为h R 23
2π，则圆锥的体积为 h R h R h R 2223
132πππ=- h R V 231π=圆锥。
