硅酸盐热工基础课件 第三章 传热原理

i 1 n
其中： i — 组分i相对于固定坐标系的速 u 度
( 3)组 i相 于 量 均 度 u或 分 对 质 平 速 者 mol平 速 uM的 度 为 扩 速 。 均 度 速 称 散 度
ui u — 组分i相对于质量平均速度的 扩散速度。
ui uM — 组分i相对于 平均速度的扩散速度。 mol
上述四个斐克定律，是 以相对于以摩尔平均速 u M，z 度 或质量平均速度 y 移动着的 u 动坐标 而言的。对于 固定 坐标 ，上述四表达式不适用 （除非为 等质量或等摩尔 逆扩散形式）
（5）可推得相对于固定坐 标的斐克定律： dy A N A C DAB y A (N A N B ) dy
二元混合物中组分 和B的分子扩散质量通量 A 大小相等方向相反
（ ）同理， A C A u A u M） 4 J （ J B C（u B u M） B 则J A J散摩尔通量 A 大小相等方向相反
工程场合下常采用相对于固定坐标的净扩散通量m或N 试验研究时多采用分子扩散通量j或J
（1）流体流动过程（动量传递）
三传理论： （2）传热过程（热量传递）
（3）传质过程（质量传递）
对传质（质量传递）的理解 质量传递过程又称扩散过程。因物质的传递过程 凭借扩散作用（分子扩散和涡流扩散）实现的。 质量传递可以在一相内进行，也可以在相际进行。 质量传递的起因是系统内存在化学势的差异。化 学势的差异由浓度、温度、压力或外加电磁场引起。 质量传递是均相混合物分离的物理基础，也是反 应过程中几种反应物互相接触及反应产物分离的基 本依据。
0.15×10-5
0.11×10-5 2.59×10-9 1.30×10-30
（2）多孔材料中的扩散

由于换热是在内管内表面，所以定性尺寸选内管内径 d = 25mm-2×2.5mm = 20mm = 0.02m
所以
Re
dw
0.02 997 0.4 90.27 105
8836
过渡流
上一内容 下一内容 回主目录
返回
= 997kg/m3 25mm 89mm
Back to
热工基础—4 传热过程
校正系数
Prf Prw
0.11
修正系数。
……(4-55)
适用条件： 2300 Re f 104;
1.5 Prf 500,
0.05 Prf 20 Prw
上一内容 下一内容 回主目录
返回
Back to
热工基础—4 传热过程
(4) 流体掠过平板湍流流动
计算公式为：
Num
(0.037
Re
0.8 m
0.023 d
wd
0.8
cp 0.4
… …
※(4-50)
※
上一内容 下一内容 回主目录
返回
Back to
热工基础—4 传热过程
0.023
d
wd
0.8
cp
0.4
…… ※(4-49) ※
定性条件：定性温度为流体平均温度，定性尺寸为管子内径。
适用条件：
① 湍流区 Ref > 104 。 过渡区需乘以校正系数 f
13 :
2030
上一内容 下一内容 回主目录
不适合长管
返回
Back to
热工基础—4 传热过程
(3) 流体在圆管内过渡流流动 ① 对气体
计算公式为：
Nu f
0.0214(Re0f.8

对流传热
综合传热
课件目录
教案
1
4.4.2热辐射的基本定律
硅 酸 盐 工 业 热 工 基 础
4.4.2.1普朗克辐射定律
（1）辐射能力和辐射强度
物体每单位表面积，在单体时 间内向半球空间辐射出去的波 长从0～∞范围内的总能量 符号：“E”
辐射能力
单位：W/m2
辐射强度
物体每单位表面积，在单体时 间内向半球空间辐射出去的波 长从λ～dλ范围内的辐射能力为 dE，dE与波长间隔的比值
因为管道表面积F1相对于厂房面积F2来说是很小
F1 0 F2
ε
12≈ε 1
12 1
T 4 T T T Qnet ,12 12 C0 [( 1 ) 4 ( 2 ) 4 ] 1 F1C0 [( 1 ) 4 ( ) ]F1 100 100 100 100
T T ql 1C 0 [( 1 ) 4 ( 2 ) 4 ]d 100 100
4.4辐射传热 硅 酸 盐 工 业 热 工 基 础
4.4.1辐射传热的基本概念
4.4.1.1辐射传热的本质和特点
辐射
物体以电磁波的方式向外传递能量的过程
电磁波谱
对流传热
综合传热
课件目录
教案
1
硅 酸 盐 工 业 热 工 基 础
热辐射 热射线 辐射传热
由于热的原因而发生的辐射
取决于温度
能被物体吸收并转变成热能的部分电磁波 物体之间相互辐射和吸收热过程的总效果
空间热阻
1 12 F1
黑休辐射传热 的电热网络图
E01 E02
对流传热
综合传热
课件目录
教案
1
4.4.3.3灰体间的辐射传热

1200 K
1400 K
λ
0
1
上一内容
2
下一内容
3
回主目录
4
5
返回
6
(µm)
热工基础—4 传热过程
对 λ ~ Eλ 曲线的讨论： (1) 某一波长的单色辐射能力随温度升高而增大；
(2) 在某一温度下，其辐射能力随波长而变化： λ＝0，Eλ，0＝0；λ↑，Eλ，0↑； 达到最高值后，λ↑，Eλ，0↓。 (3) 温度愈高，最大辐射强度的波长愈短
A0 , E0 , T0
E0(1-A1) E0(1-A1)
E0A1
对于任意物体，发射与吸收的能力差额为
q = E1 − A1 E0
当两壁的辐射达到平衡时，物体吸收与发射的能量相等
E1 = A1 E0
上一内容 下一内容
E1 = E0 A1
回主目录
E1 Ⅱ 返回
E1 Ⅰ
热工基础—4 传热过程
克希霍夫定律：
区 分辐射 能力 E 与单色辐射能力 El0，以及 4.4.2.3 斯蒂芬—波尔兹曼定律 (四次方定律) 数学表达式：
T 4 E0 = C0 ( ) ……(4-69) 100
(W/m2)
C0 = 5.669W /(m2·K4)
物理意义：说明黑体的辐射能力与其绝对温度的四次方成正比 。 上一内容 下一内容 回主目录
② 完整性
完整性
Q11 + Q12 + Q13 + ⋅⋅⋅⋅⋅⋅⋅ + Q1n = Q1 Q1n Q11 Q12 Q13 + + + ⋅⋅⋅⋅⋅⋅ + =1 Q1 Q1 Q1 Q1
ϕ11 + ϕ12 + ϕ13 + ⋅⋅⋅⋅⋅⋅ +ϕ1n = 1

(1) 传统窑炉（非中空窑）： tw1 tm（tm是物料温度，由工艺制度规定） 属于第一类边界条件（温度已知）。
(2) 现代窑（如梭式窑、辊道窑、中空窑等）： tf>tw1>tm，属于第二类边界条件（q = const）
• • 关于外壁面散热
已知tw2，属于第三类边界条件。
Q 综2 tw2 t f 2 Fw
值计算；
(b) 修改数学模型。
2.5
• 其中自由对流不仅取决于流体的物性和过程 强度，还取决于空间的形状和大小，对流换 热系数包括有两个壁面上的对流换热以及空 气层的导热。
• 隔热作用评价标准：
(1) RQ
(2) t
(3) t w2
• 因为高温区辐射很强，所以在高温区不能利 用空气夹层来隔热。
• • 由内壁面温度tw1计算散热
Qnet,
fm


fmC0

Tf 100
4


Tm 100
4

Fm
其中火焰至物料系统导来黑度：
fm

f
f m[1 wm (1 f )] wm (1 f )[m f (1 m )]
式中 wm

Fm Fw
若考虑火焰对物料的对流换热，则净热量：
(3) 窑墙外表面向外界大气的对流和辐射传热。
其热—电模拟电路：
R对1
R对2
tf1 •
•tw1
tw2•
• tf2
R辐1
R导
R辐2
Q
三个子过程：
(1) 流体1壁面w1
Q 综1 t f 1 tw1 Fw
[W]
其中： 综1 对1 辐1

始压力p1＝7×105Pa，温度t1=20℃。因泄漏，后 压力降至p2＝4.9×105Pa ，温度未变。问漏去多少
氧气？
解：取钢瓶的容积为系统（控制容积），泄漏过 程看成是一个缓慢的过程。初终态均已知。假定 瓶内氧气为理想气体。根据状态方程:
精选ppt
8
二. 理想气体的比热容
物体温度升高1K所吸收的热量称为热容； 一单位质量的物体温度升高（或降低）１℃所吸 收（或放出）的热量称为（质量）比热容。
2) 理想气体： pvRgT cpcv Rg
uf(T) hf(T)
kcp cv
ucv T; hcp T
s c vln T T 1 2 R lnv v 1 2; s cpln T T 1 2 R lnp p 1 2
3)可逆过程：
w pdv 精选ppt
w t vdp
q
Tds
37
分析热力过程的步骤：
讨论：
1、比较教材P75例3-4的解法，上面是利用基本 定义来解的，显然要容易得多，不需记忆相关换算公 式；
2、若本题不要求折合摩尔质量，仅要求折合气 体常数，则也可用：
Rg,eq wiRg,i
i
精选ppt
34
作业：P103-104
3-10 3-15
思考题: P102
10
精选ppt
35
五. 理想气体的基本热力过程
1.热力学能的变化量： u cvdT
若比热容取定值或平均值，有： u cvT
2.焓的变化量： hcpdT
u cV
T T2
T1
若比热容取定值或平均值，有： h cpT
h cp
T2 T1
T
精选ppt
21
3. 理想气体熵变化量的计算：

具。
P7
1. 绪论
❖ 新石器时代—1万年前，人类对石头进行加工 ❖ 金坛三星村新石器时代遗址
❖ 孟津妯娌新石器时代聚落遗址
P8
P9
P10
P11
1. 绪论
❖(三) 青铜器时代 Bronze Age：人类大量制造和使用第二 种人造材料——“红铜”和“青铜”。
❖ 烧制陶器过程中还原出金属铜和锡，创造了炼铜技术， 生产出各种青铜器物，进入了青铜器时代。
P13
1. 绪论
❖(三) 铁器时代 Iron Age：人们开始使用铁来制造工具和 武器的时代。
❖ 人类制造和使用的第三种人造材料——铸铁，此后是钢 铁工业的迅猛发展，成为18世纪产业革命的重要内容和 物质基础。冶炼青铜的基础上逐渐掌握了冶炼铁的技术 之后，铁器时代就到来了。
❖ 世界上最早使用铁器是小亚细亚的赫梯人在公元前1400 年左右，古希腊和古罗马开始普遍使用在公元前1000年。 中国最早在春秋战国－晋国(大致公元前700年)，铁器的 广泛使用，使人类的工具制造进入了一个全新的领域， 生产力得到极大的提高。
P23
1. 绪论
❖ 硅酸盐材料主要是指由SiO2及其硅酸盐化合物为主要成 分制成的材料，包括陶瓷、玻璃、水泥和耐火材料等。
❖ 1、陶瓷
❖ 中国是世界著名的陶瓷古国，早在八千年前的新石器时 代，我国的先民就已经会制造和使用陶瓷了。陶瓷一般 是由黏土、长石、石英或其他原料经粉碎、混合、成型、 干燥、烧制而成的制品的统称。
❖ 人类对材料的应用一直是社会文明进程的里程碑。纵观 人类发展和材料发展的历史，可以清楚地看到，每一种 重要新材料的发现和利用都会把人类支配和改造自然的 能力提高到一个新 古代的石器、青铜器、铁器等的兴起和广泛利用，极大 地改变了人们的生活和生产方式，对社会进步起到了关 键性的推动作用，这些具体的材料(石器、青铜器、铁 器)被历史学家作为划分某一个时代的重要标志，即石 器时代、青铜器时代、铁器时代等。

16
3 导热微分方程
[依据] (1) 傅立叶导热定律； (2) 热力学第一定律——能量守恒定律。
[推导过程]
(1) 物体内无内热源 如图
假定物体各向同性，、cp、为常数，则在同
一时间内，根据能量守恒定律，得如下关系式：
热焓的增量＝传入物体热量－传出物体热量
17
微元六面体：dv＝dxdydz
d时间内x方向传入热量：
则根据傅立叶定律，可求出任一瞬间通过物体
表面dF传出的热量为：
dQ

w
t n
dF
26
例如：
(a) 无限大 有限厚平板 内导热
t1 •
Q
• t2
(b) 非中空窑： tf twtm twtm
tm
tf
tw
••
•
27
第二类边界条件：已知任何时刻通过物体边界面
上的热流qw，即相当于已知任 何时刻边界面上的温度梯度。
0
0
若过程开始时，物体内各部分温度相等，则 初始条件为：
t 0 t0（常数）
25
• 边界条件——物体边界上过程进行的特点，反 映边界与周围环境相作用的条件。
常见的边界条件有三类： 第一类边界条件：已知任何时刻边界上的温度
即： tw const （稳定）
tw f ( ) （不稳定）
(3) 已知Q、R，求t，进而求 t1 或 t2 。 32
单层平壁（变物性）：
= 0(1+t）
其中：t t1 t2 2
根据傅立叶定律得：
q

0
(1

t
)
dt dx
分离变量并积分得： q

t q
q 1
t t t t t1 t2 2 2 3 3 3 4 s1 s2 s3
t1
t2
1
0
t3
3
将上式变形，有
t1 t2 q t 2 t3 q
t3 t4 q
1
s1
2
t4
x
t4
2
3
q t1 t4 s1 s2 s3
s2
s1
t1
q dt dx
含义：物体温度梯度为 1℃/m 时，单位时间、单位面积上的导热量

K) ℃) — 热导率 W/(m· 或 W/(m·
物质的热导率由实验测定，其中，金属热导率 > 合金 > 非金属材料、液体 > 气体
上一内容
下一内容
回主目录
返回
热工基础—4 传热过程
4.2.2.1 固体的热导率 (1) 金属 λ= 2.3～427 w/m.℃，纯银最大，纯铜、铝次之 特点：t↑, λ↓ λ纯金属 >λ合金
s s ，3 t1 q 1 2 t 1 1 2
s1
将计算出得温度与假设的温度比较，如果误差超过假定温度的 5%，则需要从新计算。
上一内容 下一内容 回主目录
返回
热工基础—4 传热过程
例题：4-2 设有一窑墙，用黏土砖和红砖两种材料砌成，厚度均为200mm，内壁温度为1200℃ ，外壁温度为100℃，红砖的使用温度为800℃，试求通过每平方米窑墙的热损失及在此 条件下红砖能否使用？ 已知：红砖热导率 t 0.465 0.44 103 t
s1 / 1
s2
t3
s2 / 2
s3
s3 / 3

导热系数
总结词
导热系数是描述介质导热性能的物理量。
详细描述
导热系数定义为单位时间内，通过单等条件。导热系数越大，介质的导热性能越好。常见的物 质导热系数从大到小排列为：铜、铝、铁、玻璃、木材等。
稳态导热
总结词
稳态导热是指介质中的温度分布不随时间变化的传热过程。
传热的基本原理 和规律课件
contents
目录
• 传热的基本概念 • 热传导原理 • 对流换热原理 • 辐射换热原理 • 传热规律的应用
01
CATALOGUE
传热的基本概念
传热定义
传热定义
传热是指热量从高温物体传递到 低温物体，或从一个物体的高温
部分传递到低温部分的过程。
传热分类
根据传热机理，传热可分为热传导、 热对流和热辐射三种基本类型。
热性能的参数。
辐射
辐射是指热量通过电磁波传递的 过程。辐射换热系数是表征物体 之间通过辐射进行热量传递的性
能参数。
传热过 程
热量平衡
在传热过程中，热量从高温物体 传递到低温物体，最终达到温度 平衡状态。
传热速率
传热速率受到多种因素的影响， 如物体的物理性质、传热方式、 温度差等。
02
CATALOGUE
详细描述
在稳态导热过程中，介质内部没有热量积累，热量传递速率与热量生成或损失 速率相等。此时，介质内部的温度分布只与位置有关，而与时间无关。常见的 稳态导热现象包括物体的散热、地温梯度的形成等。
03
CATALOGUE
对流换热原理
对流换热定义
对流换热是指流体与固体壁面直接接 触时，由于温度差的存在而发生的热 量传递过程。
传热规律的应用
工业传热

硅
4.1传热基本概念
酸
盐
工
传热 热量传递的过程
业
热 工
基本条件 物体间存在温度差
基 础
q k t Rt
低温端
高温端
1
第1页/共12页
硅
酸 盐
（1） 传导传热：依靠物体微观粒子的热运动而传递热量。
工 业
特点：
热
物体各部位不发生宏观相对位移
工
基
础 热量从铁丝的高
温端传递到低温端，
但铁丝外观未变化。
1
定义：温度场中，两等温面间温度差与其法线方向
两等温面间距离比值的极限。
1
第9页/共12页
硅
数学表达式：
酸
t-Δt t t+Δt
盐 工
gradt t n
(℃/m)
业
热
工
单向稳定温度场：
基
础
gradt dt (℃/m)
dx
注意：温度梯度方向
指向温度升高方向，
与热流方向相反
1
第10页/共12页
硅
酸 盐
第2页/共12页
（2）对流传热：依靠流体质点的宏观位移而传热。
硅
酸
单纯对流传热 发生于流体内、流体之间
盐
工
对流换热
流体与固体表面之间的传热
业
热
工
基 础
火焰通过周围气体 的运动对流能将热
量从周围向其它地
方传递
1
第3页/共12页
（3）辐射传热：不借助于媒介物，热量以热射线形式从
硅 酸
高温物体传向低温物体
盐
工
业
热
工
基
础

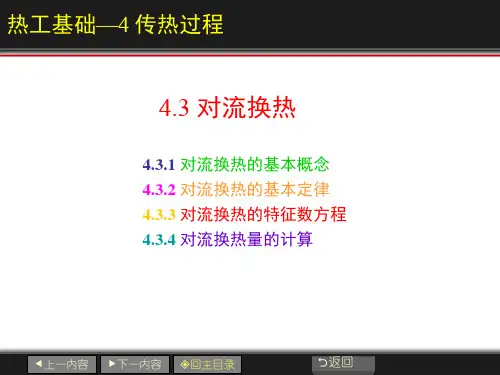
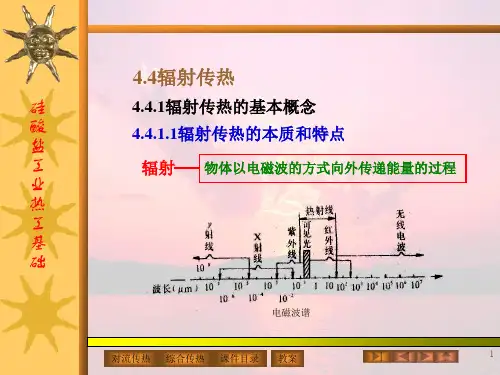
对于二元混合物，有 即
N A ,z D AB C dy A y A ( N A , z N B, z ) dz
A的实际 传质通量 同理： m A ,z
A的分子 扩散通量
A的主体 流动通量
dw A D AB w A ( m A , z m B, z ) dz
§3-1 分子扩散基本定律
式(3-15)中，若NA=-NB(称该类型的扩散为等摩尔逆扩散)，则有
NA NB 0
且
NA J A
JA JB 0
这说明等摩尔逆扩散时，无混合物整体流动，只有由浓度梯度 推动的分子扩散。
例3-2 温度为25C，总压力为105Pa的甲烷-氦(CH4-He)混合物盛于 一容器中，其中某点的甲烷分压为0.6105Pa，距离该点2.0cm处的 甲烷分压降低为0.2105Pa。设容器中总压恒定，扩散系数为 0.675cm2/s，试计算甲烷在稳态时分子扩散的摩尔通量。 解：容器中的系统为二元扩散系统，设甲烷为A组分，氦为B组分 因总压力为常数，根据理想气体状态方程斐克定律可写为， P d A dC A D dP RT J A ,z D AB D AB AB A dz dz RT dz 甲烷在z方向z1、z2处的分压分别为 PA,1= 0.6105Pa， PA,2= 0.2105Pa， 则稳态扩散时甲烷分子扩散的摩尔通量为
§3-1 分子扩散基本定律
应用理想气体状态方程，物质的量浓度可表示为：
Ci ni P i V RT n P C V RT
(3-4) (3-5)
式中，Pi、P为组分i的分压力和混合气体的总压力； ni、n为组分i的物质的量和混合气体总的物质的量；
V为混合气体的体积；