动量守恒定律应用人船模型共20页文档

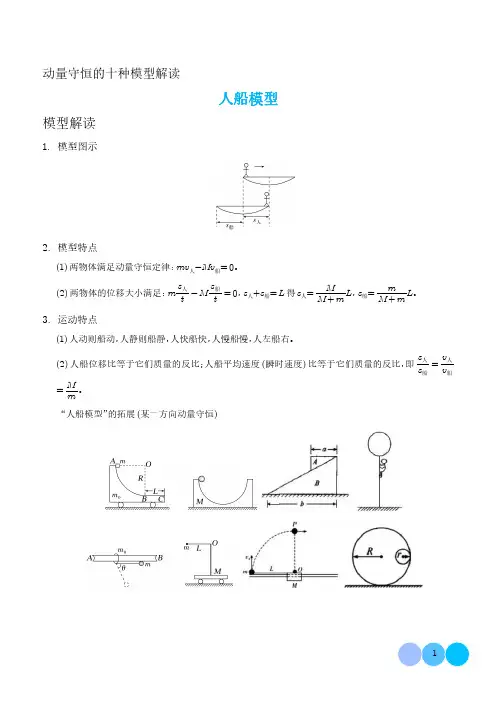
动量守恒的十种模型解读人船模型模型解读1.模型图示2.模型特点(1)两物体满足动量守恒定律：mv 人-Mv 船=0。

(2)两物体的位移大小满足：m s 人t -M s 船t =0，s 人+s 船=L 得s 人=M M +m L ，s 船=m M +mL 。

3.运动特点(1)人动则船动，人静则船静，人快船快，人慢船慢，人左船右。

(2)人船位移比等于它们质量的反比；人船平均速度(瞬时速度)比等于它们质量的反比，即s 人s 船=v 人v 船=M m 。

“人船模型”的拓展(某一方向动量守恒)【典例分析】1如图，质量为M 的匀质凹槽放在光滑水平地面上，凹槽内有一个半椭圆形的光滑轨道，椭圆的半长轴和半短轴分别为a 和b ，长轴水平，短轴竖直。

质量为m 的小球，初始时刻从椭圆轨道长轴的右端点由静止开始下滑。

以初始时刻椭圆中心的位置为坐标原点，在竖直平面内建立固定于地面的直角坐标系xOy ，椭圆长轴位于x 轴上。

整个过程凹槽不翻转，重力加速度为g 。

(1)小球第一次运动到轨道最低点时，求凹槽的速度大小；(2)凹槽相对于初始时刻运动的距离。

【针对性训练】1(2024河南名校联考).如图，棱长为a 、大小形状相同的立方体木块和铁块，质量为m 的木块在上、质量为M 的铁块在下，正对用极短细绳连结悬浮在平静的池中某处，木块上表面距离水面的竖直距离为h 。

当细绳断裂后，木块与铁块均在竖直方向上运动，木块刚浮出水面时，铁块恰好同时到达池底。

仅考虑浮力，不计其他阻力，则池深为()A.M +m M hB.M +m m (h +2a )C.M +m M (h +2a )D.M +m Mh +2a 2(2024全国高考模拟)一小船停靠在湖边码头，小船又窄又长(估计重一吨左右)。

一位同学想用一个卷尺粗略测定它的质量，他进行了如下操作：首先将船平行于码头自由停泊，轻轻从船尾上船，走到船头停下，而后轻轻下船。

用卷尺测出船后退的距离d ，然后用卷尺测出船长L 。

高中物理教研论文巧解人船模型问题(最全)word资料巧解人船模型问题——平均动量守恒定律的应用1．平均动量守恒定律当系统在全过程中动量守恒时，则这一系统在全过程中的平均动量也守恒。

在符合动量守恒的条件下，如果物体做变速运动，为了求解位移，可用平均动量及其守恒规律来处理。

2. 人船模型如果系统是由两（或多）个物体组成的，合外力为零，且相互作用前合动量为零，我们称为人船模型。

(1)一人一船模型：如图1所示人由左端走到右端的过程中， 由动量守恒定律，得 02211=-v m v m由于在全过程动量都守恒，所以有 0211=---v m v m同乘以时间t ，得 0211=---t v m t v m即 2211s m s m =此为一人一船模型的平均动量守恒方程，且知位移与质量成反比。

又由图知 L s s =+21，解得两物体位移分别为L m m m s 2121+= Lm m m s 2112+=（2）二人一船模型：如图2所示，a 、b 两人交换位置过程中，设船c 向左运动，同理可得平均动量守恒定律的方程c c b b a a s m s m s m +=3．一题三法求解人船模型例题 如图2所示，a 、b 两人质量分别为a m 和b m ，船c 的质量为c m ，船长为L ，现在a 、b 交换位置，求船c 在该过程的位移？法1 由二人一船模型得 c c b b a a s m s m s m +=位移关系 L s s c a =+ L s s c b =-联立解得Lm m m m m s cb a ba c ++-=此解法作图较简单，但位移关系和解方程都较复杂。

法2 如图3所示，先令b 不动，a 走到右端，由一人一船模型，得 Lm m m m s cb a ac ++=1再令a 不动，让b 走到左端，在该过程中同理可得L m m m m s cb a bc ++=2由图知L m m m m m s s s cb a ba c c c ++-=-=21此解法把问题化为两个一人一船模型，根据位移和质量的反比关系可直得到结果。

动量守恒的条件爆炸、反冲运动人船模型考点一动量守恒的条件考点二爆炸、反冲运动考点三人船模型考点四连续射击问题1．动量守恒定律内容：如果一个系统不受外力，或者所受外力的矢量和为0，这个系统的总动量保持不变。

2．动量守恒定律常用表达式：m1v1＋m2v2＝m1v1′＋m2v2′.1)p＝p′：相互作用前系统的总动量p等于相互作用后的总动量p′.2)m1v1＋m2v2＝m1v1′＋m2v2′：相互作用的两个物体组成的系统，作用前动量的矢量和等于作用后动量的矢量和．3)Δp1＝－Δp2：相互作用的两个物体组成的系统，一个物体的动量变化量与另一个物体的动量变化量大小相等、方向相反．4)Δp＝0：系统总动量增量为零．考点一动量守恒的条件⑴系统不受外力或者所受外力之和为零；⑵系统受外力，但外力远小于内力，可以忽略不计；⑶系统在某一个方向上所受的合外力为零，则该方向上动量守恒。

⑷全过程的某一阶段系统受的合外力为零，则该阶段系统动量守恒。

附：机械能守恒的条件：只有重力、系统内弹力做功．1．下列四幅图所反映的物理过程中，说法正确的是（）A．甲图中子弹射入木块过程中，子弹和木块组成系统动量守恒，能量不守恒B．乙图中M、N两木块放在光滑水平面上，剪断束缚M、N的细线，在弹簧从压缩状态恢复原长过程中，M、N与弹簧组成的系统动量不守恒，机械能守恒C．丙图中细线断裂后，木球和铁球在水中运动的过程，两球组成的系统动量不守恒，机械能守恒D．丁图中木块沿光滑固定斜面下滑，木块和斜面组成的系统动量守恒，机械能守恒2．如图所反映的物理过程中，以物体A和物体B为一个系统符合系统机械能守恒且水平方向动量守恒的是（）A．甲图中，在光滑水平面上，物块B以初速度v0滑上上表面粗糙的静止长木板AB．乙图中，在光滑水平面上，物块B以初速度v0滑下靠在墙边的表面光滑的斜面AC．丙图中，在光滑水平上面有两个带正电的小球A、B相距一定的距离，从静止开始释放D．丁图中，在光滑水平面上物体A以初速度v0滑上表面光滑的圆弧轨道B3.(多选)如图所示，A、B两物体质量之比为m A∶m B＝3∶2，原来静止在足够长的平板小车C上，A、B间有一根被压缩的弹簧，地面光滑．当两物体被同时释放后，则( )A．若A、B与平板车上表面间的动摩擦因数相同，则A、B组成系统的动量守恒B．若A、B与平板车上表面间的动摩擦因数相同，则A、B、C组成系统的动量守恒C．若A、B所受的摩擦力大小相等，则A、B组成系统的动量守恒D．若A、B所受的摩擦力大小相等，则A、B、C组成系统的动量守恒4. （2021·全国乙卷·T14）如图，光滑水平地面上有一小车，一轻弹簧的一端与车厢的挡板相连，另一端与滑块相连，滑块与车厢的水平底板间有摩擦。

O O ′ A B O ″ O bR 2R 人、船问题模型(C)动量守恒定律的两个推论：推论1：当系统的动量守恒时，任意一段时间内的平均动量也守恒；推论2：当系统的动量守恒时，系统的质心保持原来的静止或匀速直线运动状态不变。

例题、如图所示，长为l 、质量为M 的小船停在静水中，一个质量为m 的人立在船头，不计水的阻力。

当人从船头走到船尾的过程中，船和人对地的移位各是多大？ 解一：设人行走的平均速度为v 1，在时间t 内从船头走到船尾对地位移为S 1，人行走时航速(平均)为v 2，位移为S 2，据动量守恒有 mv 1-Mv 2=0即 mS 1/t-MS 2/t=0 ∴S 1/S 2=M/m而S 1+S 2=l 解得S 1=Ml/(M+m) S 2=ml/(M+m)解二：系统质心位置保持不动，开始时人、船质心为O ′。

且OO ′=A O M m ', OO ′+O ′A=l/2 ∴ l m M M O O +=' 当人从船头走到船尾时，由于对称2l m M m O O ⋅+='' ∴ 船的位移l m M m O O S ⋅+='=22, l mM M S l S ⋅+=-=21 1．静止在空中的气球质量为M ，下面拖一条质量不计的软梯，质量为m 的人站在软梯上端距地面高为h 。

求：⑴人安全不能确定地面软梯的最小长度⑵若软梯长为h ，则人从软梯上端到下端时，人距地面还有多高？2．一质量为M 、底面边长为b 的三角形劈块静止于光滑水平地面上，如图。

有一质量为m 的物块由斜面顶部无初速滑到底部的过程中，劈块移动的距离是多少？3．某人在一只静止于水面上的小船上练习射出。

船、人连同枪(不包括子弹)及靶的总质量为M ，靶立于船头，枪内有n 颗质量均为m 的子弹，枪口到靶的距离为l ，子弹射出枪口时相对地面的速度为v ，在发射后一颗子弹时，前一颗子弹已陷入靶中，则在发射完n 颗子弹后小船后退的距离是多少？4．质量为m 、半径为R 的小球，放在半径为2R 、质量为2m 的大空心球内，大球开始静止在光滑水平面上。

动量守恒的十种模型解读和针对性训练人船模型模型解读1.模型图示2.模型特点(1)两物体满足动量守恒定律：m v 人－M v 船＝0。

(2)两物体的位移大小满足：m s 人t －M s 船t ＝0，s 人＋s 船＝L 得s 人＝M M ＋m L ，s 船＝mM ＋m L 。

3.运动特点(1)人动则船动，人静则船静，人快船快，人慢船慢，人左船右。

(2)人船位移比等于它们质量的反比；人船平均速度(瞬时速度)比等于它们质量的反比，即s 人s 船＝v 人v 船＝M m。

“人船模型”的拓展(某一方向动量守恒)【典例分析】【典例】 如图，质量为M 的匀质凹槽放在光滑水平地面上，凹槽内有一个半椭圆形的光滑轨道，椭圆的半长轴和半短轴分别为a 和b ，长轴水平，短轴竖直。

质量为m 的小球，初始时刻从椭圆轨道长轴的右端点由静止开始下滑。

以初始时刻椭圆中心的位置为坐标原点，在竖直平面内建立固定于地面的直角坐标系xOy ，椭圆长轴位于x 轴上。

整个过程凹槽不翻转，重力加速度为g 。

(1)小球第一次运动到轨道最低点时，求凹槽的速度大小；(2)凹槽相对于初始时刻运动的距离。

答案　(2)maM ＋m 解析　(1)小球从静止到第一次运动到轨道最低点的过程，小球和凹槽组成的系统水平方向上动量守恒，有0＝m v 1－M v 2mgb ＝12m v 21＋12M v 22联立解得v 2(2)根据人船模型规律，在水平方向上有mx 1＝Mx 2又由位移关系知x 1＋x 2＝a解得凹槽相对于初始时刻运动的距离x 2＝ma M ＋m。

【名师点拨】应用“人船模型”解题的两个关键点(1)“人船模型”的应用条件：相互作用的物体原来都静止，且满足动量守恒条件。

(2)人、船位移大小关系：m 人x 人＝m 船x 船，x 人＋x 船＝L (L 为船的长度)。

【针对性训练】1. （2024河南名校联考）.如图，棱长为a 、大小形状相同的立方体木块和铁块，质量为m 的木块在上、质量为M 的铁块在下，正对用极短细绳连结悬浮在平静的池中某处，木块上表面距离水面的竖直距离为h 。