matlab绘制三维曲面并赋予权值的方法

matlab 自由曲面
在MATLAB中，可以使用不同的方法来生成和绘制自由曲面。

以下是一些常用的方法：
1. 参数化曲面，可以使用参数方程来定义自由曲面。

例如，对于一个参数化曲面，可以使用u和v作为参数，然后定义x(u,v), y(u,v), z(u,v)作为曲面的坐标函数。

然后在MATLAB中使用meshgrid和surf函数来绘制参数化曲面。

2. 曲面拟合，如果已有一组离散的点，可以使用曲面拟合的方法来生成自由曲面。

MATLAB提供了fit函数来进行曲面拟合，可以选择不同的拟合模型，如多项式拟合、样条拟合等。

3. 三角网格曲面，对于复杂的自由曲面，可以使用三角网格来表示。

MATLAB提供了triangulation函数来创建三角网格，然后可以使用trisurf函数来绘制三角网格曲面。

4. 曲面绘制工具箱，MATLAB还提供了Curve Fitting Toolbox 和Partial Differential Equation Toolbox等工具箱，这些工具箱中包含了更多高级的曲面生成和绘制函数，可以根据具体需求选
择合适的工具箱来生成自由曲面。

总之，在MATLAB中可以根据具体需求选择不同的方法来生成和绘制自由曲面，可以根据曲面的特点和数据的特点来选择合适的方法。

希望以上信息能够帮助到你。

MA TLAB教程：教你画三维曲线三维图形（含图形处理）制作三维动画三维曲线plot3函数与plot函数用法十分相似，其调用格式为：plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)其中每一组x,y,z组成一组曲线的坐标参数，选项的定义和plot 函数相同。

当x,y,z是同维向量时，则x,y,z 对应元素构成一条三维曲线。

当x,y,z是同维矩阵时，则以x,y,z对应列元素绘制三维曲线，曲线条数等于矩阵列数。

例绘制三维曲线。

程序如下：t=0:pi/100:20*pi;x=sin(t);y=cos(t);z=t.*sin(t).*cos(t);plot3(x,y,z);title('Line in 3-D Space');xlabel('X');ylabel('Y');zlabel('Z');三维曲面1．产生三维数据在MA TLAB中，利用meshgrid函数产生平面区域内的网格坐标矩阵。

其格式为：x=a:d1:b; y=c:d2:d;[X,Y]=meshgrid(x,y);语句执行后，矩阵X的每一行都是向量x，行数等于向量y的元素的个数，矩阵Y的每一列都是向量y，列数等于向量x的元素的个数。

2．绘制三维曲面的函数surf函数和mesh函数的调用格式为：mesh(x,y,z,c)：画网格曲面，将数据点在空间中描出,并连成网格。

surf(x,y,z,c)：画完整曲面，将数据点所表示曲面画出。

一般情况下，x,y,z是维数相同的矩阵。

x,y是网格坐标矩阵，z 是网格点上的高度矩阵，c用于指定在不同高度下的颜色范围。

例绘制三维曲面图z=sin(x+sin(y))-x/10。

程序如下：[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标z=sin(x+sin(y))-x/10;mesh(x,y,z);axis([0 4*pi 0 4*pi -2.5 1]);此外，还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。

MATLAB程序设计作业陈杰杰2013090302072014-11-3MATLAB具有强大的图形处理功能。

下面给出了3个m脚本文件，请在MA TLAB环境下运行，观察其输出。

要求根据每个m文件输出的图形（共18个），用中文翻译并解释产生每个输出图形的函数具体是什么？其功能是什么？文件1：clear all %清除工作区间所有的变量clf %清除图形窗口的内容mfilename('fullpath') %返回当前正在运行的函数所在文件的文件名（全部路径）echo on %显示M文件执行的每一条命令subplot(2,3,1) %使（2*3）幅子图中第一个子图成为当前图t = 0:0.1:10; %将以0为起点、以10为终点、以0.1为步长的一维矩阵赋值给t z = impulse(1, [1 1 1], t); %动力系统的脉冲响应数据，以时间t步长0.1为单位stairs(t(1:5:end),z(1:5:end)) %绘制阶梯状图,从第1行开始，间隔5行取1行，到最后1行为止hold on %保持当前坐标轴和图形，并接受下一次绘制plot(t,z,'r') %用红线绘制横轴为t、纵轴为z的二维函数图plot([0 t(end)], [0 0], 'k:') %用黑色虚线绘制函数图像，要求经过原点平行于横轴、取值范围为0到t的最后一个值title('Impulse Response - (STAIRS)') %将此图命名为Impulse Response - (STAIRS)（脉冲响应-（阶梯图））subplot(2,3,2) %使（2*3）幅子图中第二个子图成为当前图theta = 2*pi*(0:74)/75; %将以0为起点、以2*pi*74/75为终点、2*pi/75为步长的一维矩阵赋值给thetax = cos(theta); %计算cos(theta)的值，并赋给xy = sin(theta); %计算sin(theta)的值，并赋给yz = abs(fft(ones(10,1), 75))'; %ones(10,1)生成十行一列的全一矩阵；fft(ones(10,1), 75)进行快速傅里叶变换；z = abs(fft(ones(10,1), 75))'取幅值并转置stem3(x, y, z) %绘制三维杆状图title('Polar FFT - (STEM3)') %将此图命名为Polar FFT - (STEM3)（极坐标下快速傅里叶变换-（三维针状图））subplot(2,3,3) %使（2*3）幅子图中第二个子图成为当前图[X,Y,Z] = peaks(-2:0.25:2); %产生-2为起点、2为终点、0.25为步长的guassian分布矩阵，返回峰函数的三个坐标轴空间上的数值，X表示在x轴，Y表示在y轴，Z表示在z轴，这样每个点就对应一个（X，Y，）[U,V] = gradient(Z, 0.25); %返回二维数值梯度的U、V部分，这里的0.25指定了沿着梯度的方向取点的间隔为0.25contour(X,Y,Z,10); %绘制矩阵Z的等高线，绘制的等高线被限定在由X、Y指定的区域内，等高线条数为10hold on %保持当前坐标轴和图形，并接受下一次绘制quiver(X,Y,U,V); %使用箭头来直观的显示矢量场，该调用格式表示通过在(X, Y)指定的位置绘制小箭头来表示以该点为起点的向量(U,V)title('Surface Gradient - (CONTOUR & QUIVER)') %将此图命名为Surface Gradient - (CONTOUR & QUIVER)（表面梯度-（等高线图和矢量场图））theta = 0:0.1:4*pi; %将以0为起点、以4*pi为终点、0.1为步长的一维矩阵赋值给theta[x,y] = pol2cart(theta(1:5:end), theta(1:5:end)); %把极坐标(theta(1:5:end), theta(1:5:end))转换为对应的二维笛卡尔坐标(x,y),theta(1:5:end)表示从第一行到最后一行，每五行取一行subplot(2,3,4) %使（2*3）幅子图中第四个子图成为当前图polar(theta,theta) %绘制极坐标图像，第一个theta是用弧度制表示的角度，第二个theta是对应的半径axis([-13 13 -12.5 14.5]) %横坐标范围为-13到13，纵坐标范围为-12.5到14.5title('Spiral Plot - (POLAR)') %将此图命名为Spiral Plot - (POLAR)（螺旋图-极坐标图）subplot(2,3,5) %使（2*3）幅子图中第五个子图成为当前图compass(x,y) %绘制罗盘图axis([-13 13 -12.5 14.5]) %横坐标范围为-13到13，纵坐标范围为-12.5到14.5title('Direction Vectors - (COMPASS)') %将此图命名为Direction Vectors - (COMPASS)（方向矢量-罗盘图）subplot(2,3,6) %使（2*3）幅子图中第六个子图成为当前图feather(x(1:19),y(1:19)) %绘制羽状图，其中x、y表示一组向量，x是向量的横坐标（x分量），y是向量的纵坐标（y分量）。

使用matlab绘制三维图形的方法要使用MATLAB绘制三维图形，首先需要了解MATLAB中的三维绘图函数和绘图选项。

下面将介绍一些常用的绘制三维图形的方法。

1.绘制基本的三维图形要绘制基本的三维图形，可以使用以下函数：- plot3(函数：用于在三维坐标系中绘制线条。

- scatter3(函数：用于在三维坐标系中绘制散点图。

- surf(函数：用于绘制三维曲面图。

- mesh(函数：用于绘制三维网格图。

- bar3(函数：用于绘制三维条形图。

- contour3(函数：用于绘制三维等高线图。

例如，下面的代码演示了如何使用plot3(函数绘制一个三维线条图：```x = linspace(0, 2*pi, 100);y = sin(x);z = cos(x);plot3(x, y, z, 'LineWidth', 2);xlabel('X');ylabel('Y');zlabel('Z');title('3D Line Plot');```2.添加颜色和纹理在绘制三维图形时，可以使用颜色和纹理来增加图形的信息。

MATLAB 提供了一系列函数来处理颜色和纹理，如：- colormap(函数：用于设置颜色映射。

- caxis(函数：用于设置坐标轴范围。

- shading(函数：用于设置颜色插值方法。

- texturemap(函数：用于设置纹理映射方法。

例如，下面的代码展示了如何使用纹理映射来绘制一个球体：```[X, Y, Z] = sphere(50);C = colormap('jet');surface(X, Y, Z, 'FaceColor', 'texturemap', 'CData', C);axis equal;```3.绘制多个数据集要在同一张图中绘制多个数据集，可以使用hold on和hold off命令。

三维曲面的极值点三维曲面的极值点是指曲面上具有最值的点，通常包括局部极值点和全局极值点。

在数学、物理和工程等领域中，寻找曲面的极值点具有重要意义。

本文将介绍三维曲面极值点的相关概念、求解方法以及应用实例。

一、三维曲面极值点的概念三维曲面的极值点分为局部极值点和全局极值点。

1.局部极值点：在曲面上，若某个点P在局部区域内具有最大或最小值，则称该点为局部极大值点或局部极小值点。

局部极值点是局部性质的，其存在性与局部区域的选取有关。

2.全局极值点：在曲面上，若某个点P在整个曲面上具有最大或最小值，则称该点为全局极大值点或全局极小值点。

全局极值点是全局性质的，其存在性与曲面的整体形状有关。

二、三维曲面极值点的求解方法1.数值方法：数值方法是求解三维曲面极值点的一种常用方法。

通过离散化曲面，将曲面上的点表示为空间向量，并计算向量之间的距离，从而得到曲面上的局部极值点。

常见的数值方法有梯度下降法、牛顿法、共轭梯度法等。

2.解析方法：是求解三维曲面极值点的另一种方法。

通过求解曲面的偏导数，可以得到曲面上的局部极值点。

常见的解析方法有微分几何方法、多元函数求导方法等。

3.图像处理方法：图像处理方法是求解三维曲面极值点的一种较为直观的方法。

通过对比曲面上相邻像素的灰度值，可以得到曲面上的局部极值点。

常见的图像处理方法有图像增强、边缘检测、图像分割等。

三、三维曲面极值点的应用实例1.数学领域：在数学领域，三维曲面的极值点可以用于求解偏微分方程、微分几何等问题。

例如，通过求解曲面上的极值点，可以得到曲面的几何特征，如曲率、法向量等。

2.物理领域：在物理领域，三维曲面的极值点可以用于求解物理场的分布规律。

例如，在流体力学中，通过求解曲面上的极值点，可以得到流场的压力、速度等分布规律。

3.工程领域：在工程领域，三维曲面的极值点可以用于优化问题。

例如，在机械设计中，通过求解曲面上的极值点，可以得到设计方案的最优解。

综上所述，三维曲面的极值点是曲面上具有最值的点，其求解方法包括数值方法、解析方法和图像处理方法。

一、引言Matlab是一种高级技术计算语言和交互环境，被广泛用于工程、科学和数学领域的计算与模拟。

在Matlab中，加工自由曲面是一项常见的任务，例如创建和修改三维曲面模型。

本文将介绍如何使用Matlab 编写程序代码来加工自由曲面，以实现对曲面的精确控制和调整。

二、准备工作在编写程序代码之前，首先需要明确自由曲面的定义和参数化方法。

自由曲面通常由参数方程或控制点构成，对于不同的曲面类型，需要选择合适的参数化方法。

还需要了解Matlab中与曲面加工相关的函数和工具，以便在编写程序时能够调用这些资源。

三、编写程序代码1. 定义自由曲面在Matlab中，可以使用符号变量和代数表达式定义自由曲面的参数方程。

对于二次曲面，可以使用二次多项式表示其参数方程。

具体代码如下：syms u vx = a*u^2 + b*v^2 + c*u*v + d*u + e*v + f;y = g*u^2 + h*v^2 + i*u*v + j*u + k*v + l;z = m*u^2 + n*v^2 + o*u*v + p*u + q*v + r;其中a-r为曲面的系数，u和v为曲面的参数。

2. 控制曲面形状通过调整曲面的参数和系数，可以控制曲面的形状。

可以通过改变系数a-r的值来实现对曲面的放大缩小、旋转、偏移等操作。

具体代码如下：a = 1;b = 1;c = 0;d = 0;e = 0;f = 0;g = 1; h = 1; i = 0; j = 0; k = 0; l = 0;m = 1; n = 1; o = 0; p = 0; q = 0; r = 0;这里以简单的二次曲面为例，通过调整系数的数值来控制曲面的形状。

3. 曲面绘制和可视化在定义和控制曲面之后，可以使用Matlab中的绘图函数将曲面绘制出来。

可以使用surf函数创建曲面图形，并通过设置图形属性来进行可视化调整。

具体代码如下：[u, v] = meshgrid(-2:0.1:2);x = a*u.^2 + b*v.^2 + c*u.*v + d*u + e*v + f;y = g*u.^2 + h*v.^2 + i*u.*v + j*u + k*v + l;z = m*u.^2 + n*v.^2 + o*u.*v + p*u + q*v + r;surf(x, y, z);四、应用实例在实际应用中，自由曲面加工可以用于创建各种复杂的曲面模型。

[Matlab绘图][三维图形][三维曲线基本函数+三维曲⾯+其他三维图形]1.绘制三维图形的基本函数最基本的三维绘图函数为plot3；plot3与plot⽤法⼗分相似，调⽤格式：plot(x1,y1,z1,选项1，x2,y2,z2,选项2，...，xn,yn,zn,选项n)当x,y,z是同维向量时，则x，y,z,对应元素构成⼀条三维曲线；当x,y,z是同维矩阵时，则以x,y,z对应列元素绘制三维曲线，曲线条数等于矩阵列数。

例：程序如下：t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('x'),ylabel('y'),zlabel('z');grid; 运⾏结果：2.三维曲⾯2.1平⾯⽹格坐标矩阵的⽣成 绘制z=f(x,y)所代表的三维曲⾯图，先要在xy平⾯选定⼀个矩形区域，假定矩形区域D=[a,b]*[c,d],然后将[a,b]在x⽅向分成m份，将[c,d]在y⽅向分成n份，由各划分点分别作平⾏于两坐标轴的直线，将区域D分成m*n个⼩矩形，⽣成代表每⼀个⼩矩形顶点坐标的平⾯⽹格坐标矩阵，最后利⽤有关函数绘图。

产⽣平⾯区域内的⽹格坐标矩阵有两种⽅法： 1.利⽤矩阵运算⽣成、x=a:dx:b;y=(c:dy:d)';X=ones(size(y))*x;Y=y*ones(size(x));语句执⾏后，矩阵X的每⼀⾏都是向量x，⾏数等于向量y的元素个数，矩阵Y的每⼀列都是向量y，列数等于向量x的元素个数。

于是对于矩阵X,Y来说，它们位置(i,j)上的元素值（X（i,j）,Y(i,j)）就是所要形成的平⾯⽹格在位置（i，j）上的X,Y坐标。

第十八章三维图形为了显示三维图形，MATLAB提供了各种各样的函数。

有一些函数可在三维空间中画线，而另一些可以画曲面与线格框架。

另外，颜色可以用来代表第四维。

当颜色以这种方式使用时，由于它不再象照片中那样显示信息的自然属性----色彩，而且也不是基本数据的内在属性，所以它称作伪彩色。

为了简化对三维图形的讨论，对颜色的介绍推迟到下一章。

在这一章，主要讨论绘制三维图形的基本概念。

18.1 函数plot3plot3命令将绘制二维图形的函数plot的特性扩展到三维空间。

函数格式除了包括第三维的信息（比如Z方向）之外，与二维函数plot相同。

plot3一般语法调用格式是plot3(x1,y1,z1,S1,x2,y2,z2,S2,…)，这里x n,y n和z n是向量或矩阵，S n是可选的字符串，用来指定颜色、标记符号和/或线形。

总的来说，plot3可用来画一个单变量的三维函数。

如下为一个三维螺旋线例子：» t=0:pi/50:10*pi;» plot3(sin(t),cos(t),t)» title( ‘Helix‘ ),xlabel( ‘sint(t)‘ ),ylabel(‘cos(t)‘ ),zlabel(‘ t‘ )» text(0,0,0,‘ Origin‘ )» grid» v = axisv =-1 1 -1 1 0 40输出见图18.1.图18.1 螺旋线图从上例可明显看出，二维图形的所有基本特性在三维中仍都存在。

axis命令扩展到三维只是返回Z轴界限（0和40），在数轴向量中增加两个元素。

函数zlabel用来指定z轴的数据名称，函数grid在图底绘制三维网格。

函数test(x,y,z,‘ string‘ )在由三维坐标x,y,z所指定的位置放一个字符串。

另外，子图和多图形窗口可以直接应用到三维图形中。

在最后一章可以看到，通过指定plot命令的多个参量或使用hold命令，可以把多条直线或曲线重叠画出。

一、引言在工程和科学领域中，曲面拟合是一项重要的数学和计算技术，它可以帮助研究人员或工程师从实验或观测数据中找到最佳的曲面模型，以便进行进一步的分析和应用。

在众多的曲面拟合方法中，MATLAB 作为一种强大的数学建模和计算软件，具有丰富的曲面拟合工具箱，能够进行曲面拟合并求出面积，本文将介绍如何使用MATLAB进行曲面拟合并求面积的操作方法。

二、MATLAB曲面拟合的基本原理MATLAB中的曲面拟合通常通过拟合曲面上的数据点来实现。

曲面拟合的基本原理是在给定数据点的情况下，找到一个曲面模型来最好地拟合这些数据点。

常用的曲面拟合方法包括最小二乘法、样条插值、高阶多项式拟合等。

在MATLAB中，通过调用曲面拟合工具箱中的相应函数，可以很容易地实现曲面拟合操作。

三、MATLAB曲面拟合并求面积的步骤1. 数据准备在进行曲面拟合之前，首先需要准备好要拟合的数据。

这些数据可以是实验测量得到的点，也可以是由其他方法计算得出的点。

在MATLAB中，可以将这些数据点表示为一组(x, y, z)的坐标，其中x和y表示数据点的空间位置，z表示对应这些位置的数值。

2. 曲面拟合在准备好数据后，可以使用MATLAB中曲面拟合工具箱中的函数来进行曲面拟合。

可以使用“fit”函数来拟合一个曲面模型，比如二次曲面、三次曲面或其他自定义的曲面模型。

拟合的结果可以用于后续的分析和计算。

3. 计算面积在获得曲面拟合模型之后，可以利用该模型来计算曲面的面积。

MATLAB提供了丰富的数学计算函数，可以方便地进行曲面积分和面积计算。

通过调用这些函数，可以得到拟合曲面的面积，该面积反映了原始数据点所描述的曲面的实际面积。

四、MATLAB曲面拟合并求面积的实例下面以一个简单的实例来演示如何使用MATLAB进行曲面拟合并求面积。

假设有一组数据点如下所示：```x = [1, 2, 3, 4, 5];y = [1, 2, 3, 4, 5];z = [1, 4, 9, 16, 25];```我们可以利用这些数据点来进行曲面拟合，假设我们使用二次曲面模型来拟合这些数据点：```MATLABp = polyfitn([x', y'], z, 2); % 二次曲面拟合[X, Y] = meshgrid(1:0.1:5, 1:0.1:5);Zfit = polyvaln(p, [X(:), Y(:)]);Zfit = reshape(Zfit, size(X));```通过上述代码，我们可以得到拟合曲面Zfit。

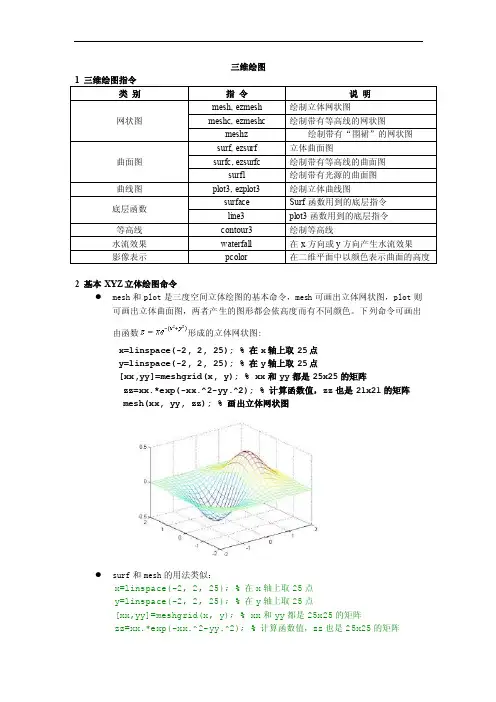
三维绘图2 基本XYZ立体绘图命令●mesh和plot是三度空间立体绘图的基本命令，mesh可画出立体网状图，plot则可画出立体曲面图，两者产生的图形都会依高度而有不同颜色。

下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值，zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似：x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值，zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图，MATLAB提供了一个peaks函数，可产生一个凹凸有致的曲面，包含了三个局部极大点及三个局部极小点，其方程式为：要画出此函数的最快方法即是直接键入peaks：peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2)●我们亦可对peaks函数取点，再以各种不同方法进行绘图。

meshz可将曲面加上围裙：[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果：[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果：[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线：[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线：[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线：contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影：contour(peaks, 20);plot3可画出三度空间中的曲线：t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线：t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);三维绘图的主要功能：绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色（一）三维线图plot3 ——基本的三维图形指令调用格式：plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’,…)二维图形的所有基本特性对三维图形全都适用。

matlab 三维曲面三角剖分（原创实用版）目录一、MATLAB 三维曲线和三维曲面的绘制二、三维曲线和曲面的三角剖分三、MATLAB 中的三角剖分函数四、应用案例：三维曲面的三角剖分五、总结正文一、MATLAB 三维曲线和三维曲面的绘制MATLAB 是一款强大的数学软件，可以方便地进行三维曲线和三维曲面的绘制。

在 MATLAB 中，我们可以使用 plot3 函数进行三维曲线的绘制，使用 mesh 和 surf 函数进行三维网格图和三维曲面图的绘制。

二、三维曲线和曲面的三角剖分在实际应用中，我们可能需要对三维曲线和曲面进行三角剖分，以便于进行更深入的分析和计算。

在 MATLAB 中，可以使用 triangulate 函数进行三角剖分。

三、MATLAB 中的三角剖分函数MATLAB 中的 triangulate 函数可以接受两个参数，分别是需要进行三角剖分的曲面坐标和分割的深度。

该函数会返回一个三角形的坐标矩阵，我们可以使用这个矩阵进行后续的计算和分析。

四、应用案例：三维曲面的三角剖分假设我们有一个三维曲面，其坐标为 (x, y, z)，我们希望将其进行三角剖分，分割的深度为 3。

我们可以使用以下代码进行三角剖分：```matlab% 曲面坐标x = [1, 2, 3, 4, 5];y = [1, 4, 6, 8, 10];z = [1, 4, 9, 16, 25];% 进行三角剖分，分割的深度为 3[X, Y, Z] = triangulate(x, y, z, 3);```运行以上代码，我们可以得到一个包含三角形坐标的矩阵，我们可以使用这个矩阵进行后续的计算和分析。

五、总结MATLAB 提供了强大的三维曲线和曲面绘制功能，同时也提供了方便的三角剖分函数。

一、概述在工程和科学领域中，对于三维空间中的点集，经常需要拟合出一个曲面方程来描述这些点的分布规律。

而MATLAB作为一种功能强大的科学计算软件，可以通过其丰富的工具箱和函数来进行三维点的拟合和曲面方程的求解。

本文将介绍MATLAB中如何进行三维点拟合曲面方程的操作和实现。

二、三维点拟合曲面方程的基本原理三维点拟合曲面方程是利用已知的三维点集，通过数学方法来拟合出一个能够较好地描述这些点分布规律的曲面方程。

常见的曲面方程包括二次曲面方程、三次曲面方程等。

通过这些曲面方程，可以更加直观地理解和分析点集的特征，也可以用于进行预测和模拟。

三、 MATLAB中实现三维点拟合曲面方程的方法在MATLAB中，可以使用Curve Fitting Toolbox来进行三维点拟合。

下面是实现这一功能的具体方法：1. 导入三维点集数据：需要将已知的三维点集数据导入MATLAB 工作空间。

2. 选择合适的曲面拟合模型：根据实际情况，选择适合的曲面拟合模型，比如二次曲面、三次曲面等。

3. 使用curve fitting工具箱进行拟合：利用MATLAB提供的curve fitting工具箱中的函数，对导入的三维点集数据进行曲面拟合操作。

4. 评估拟合效果：拟合完成后，需要对拟合效果进行评估，包括拟合误差的计算和曲面方程的可视化显示。

四、实例演示为了更好地理解MATLAB中三维点拟合曲面方程的方法，下面通过一个具体的实例来演示。

假设有一个三维点集P(x, y, z)，其中包括了10个已知点的坐标数据。

现在需要利用MATLAB来拟合出一个二次曲面方程来描述这些点的分布规律。

步骤一：导入三维点集数据在MATLAB中创建一个包含10个已知点坐标数据的矩阵P(x, y, z)，并将其导入到MATLAB工作空间中。

步骤二：选择合适的曲面拟合模型根据实际情况，选择二次曲面方程作为拟合模型。

二次曲面方程的一般形式为z = ax^2 + by^2 + cx + dy + e。

matlab中surface的用法在MATLAB中，surface函数用于绘制三维图形，包括曲面、网格图和等值图等。

它的基本语法如下：matlabsurface(X, Y, Z)其中，X、Y和Z是任意大小的矩阵，用于定义曲面的坐标。

X和Y矩阵确定曲面上每个点的水平和垂直位置，而Z矩阵定义了每个点的高度或数值。

X和Y 的大小必须与Z相同。

surface函数还有一些可选参数，可以用来自定义绘图的样式和外观，例如：- `'FaceColor'`：指定曲面的填充颜色，可以是颜色名称（如`'red'`、`'blue'`等）、RGB颜色值或颜色映射（如`'jet'`、`'hsv'`等）。

- `'EdgeColor'`：指定曲面的边缘颜色。

- `'LineWidth'`：指定曲面的线宽。

- `'FaceAlpha'`：指定曲面的填充透明度（0至1之间）。

- `'EdgeAlpha'`：指定曲面的边缘透明度（0至1之间）。

- `'FaceLighting'`：指定曲面的照明模式，可以是`'flat'`、`'gouraud'`或`'phong'`。

- `'AmbientLight'`：指定曲面的环境光强度（0至1之间）。

- `'DiffuseLight'`：指定曲面的散射光强度（0至1之间）。

- `'SpecularLight'`：指定曲面的镜面光强度（0至1之间）。

根据具体需求，你可以根据这些参数来自定义surface函数的使用。

Matlab绘制三维曲线plot3函数与plot函数用法十分相似，其调用格式为：plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)其中每一组x,y,z组成一组曲线的坐标参数，选项的定义和plot函数相同。

当x,y,z是同维向量时，则x,y,z 对应元素构成一条三维曲线。

当x,y,z是同维矩阵时，则以x,y,z对应列元素绘制三维曲线，曲线条数等于矩阵列数。

例绘制三维曲线。

程序如下：t=0:pi/100:20*pi;x=sin(t);y=cos(t);z=t.*sin(t).*cos(t);plot3(x,y,z);title('Line in 3-D Space');xlabel('X');ylabel('Y');zlabel('Z');三维曲面1．产生三维数据在MATLAB中，利用meshgrid函数产生平面区域内的网格坐标矩阵。

其格式为：x=a:d1:b; y=c:d2:d;[X,Y]=meshgrid(x,y);语句执行后，矩阵X的每一行都是向量x，行数等于向量y的元素的个数，矩阵Y的每一列都是向量y，列数等于向量x的元素的个数。

2．绘制三维曲面的函数surf函数和mesh函数的调用格式为：mesh(x,y,z,c)：画网格曲面，将数据点在空间中描出,并连成网格。

surf(x,y,z,c)：画完整曲面，将数据点所表示曲面画出。

一般情况下，x,y,z是维数相同的矩阵。

x,y是网格坐标矩阵，z是网格点上的高度矩阵，c用于指定在不同高度下的颜色范围。

例绘制三维曲面图z=sin(x+sin(y))-x/10。

程序如下：[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标z=sin(x+sin(y))-x/10;mesh(x,y,z);axis([0 4*pi 0 4*pi -2.5 1]);此外，还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。

第7讲 绘制三维图（第5章MATLAB 绘图）目的：1.掌握绘制三维图形的方法。

2.掌握绘制图形的辅助操作。

一、绘图时点坐标矩阵的生成。

绘图函数使用描点法绘图，所以在绘图前，需要建立空间点的概念，空间中的点需要三个坐标(,,)x y z ，matlab 使用三个矩阵来存储点的三个坐标，一个矩阵（比如A ）存储点的x 坐标，一个矩阵（比如B ）存储点的y 坐标，一个矩阵（比如C ）存储点的z 坐标。

其中A 、B 、C 三矩阵是同型矩阵。

例如设矩阵123112X ⎛⎫⎪= ⎪ ⎪⎝⎭，014221Y −⎛⎫ ⎪= ⎪ ⎪⎝⎭，510113Z ⎛⎫ ⎪= ⎪ ⎪−⎝⎭则，matlab 绘图函数将绘制点()()1,0,5,(2,1,1),(3,4,0),,2,1,3−共6个点。

如果点的坐标没有规律那么我们需要手工输入坐标矩阵。

如果点的坐标有规律，那么我们可以使用矩阵运算或者matlab 产生点的函数来生成坐标矩阵。

例如，假设空间中点的纵横坐标如下图所示：图中点的坐标有规律：横坐标是(1,2,3,4),纵坐标是(1,2,3)，所以可以使用如下方法得到点的坐标矩阵。

方法一：>> a=[1,2,3,4];b=[1,2,3];i=ones(1,3);j=ones(1,4);>>x=i’ *a; y=b‘ *j;方法二：使用matlab系统函数meshgrid（推荐使用）>> a=[1,2,3,4]; b=[1,2,3];>>[x,y]=meshgrid(a,b) % 该函数生成的x，y矩阵和方法一相同。

------------------我是华丽分割线-----------------除meshgrid外，还可以用peaks、cylinder函数等生成点坐标矩阵。

peaks(n): 本身是一个创建具有多个峰值的曲面图，例如:>> peaks(30) %产生的图如下：在matlab中可以使用，例如：命令[x,y,z]=peaks(30)取出曲面点的三个坐标矩阵x,y,z；[a,b]=peaks(30)取出曲面点的前两坐标矩阵x,y；%可以用逻辑运算a==x,b==y验证注意：命令a=peaks(30)取出的a不是曲面点的x坐标，而是点的z坐标；可以用二维绘图函数scatter(x,y)绘制散点图观察取出的坐标点:>>[x,y]=peaks(8);>>scatter(x,y)另一个可以用来取坐标点的函数是sphere(n)，命令sphere(n)：绘制一个具有n个纵列的单位球面。

Matlab中的3D图形绘制方法Matlab是一种常用于科学计算和数据可视化的高级编程语言和开发环境。

它的强大功能使得它成为工程师、科学家和研究人员的首选工具之一。

其中一个引人注目的特点是它对3D图形的支持。

在本文中，我们将探讨Matlab中的一些3D图形绘制方法。

Matlab提供了多种绘制3D图形的函数和工具。

最基本的方法是使用“plot3”函数绘制三维数据。

这个函数接受x、y和z三个参数，分别表示三维坐标系上的数据点。

通过给定一系列的数据点，我们可以在三维空间中绘制出线条或散点图。

这种方法适用于简单的数据展示和初步的分析。

除了基本的线条和散点图，Matlab还提供了一些更高级的3D图形绘制函数，如“surface”和“mesh”。

这些函数可以用来绘制三维曲面和网格图。

例如，我们可以使用“surface”函数绘制一个三维山丘的图像，其中x和y轴表示地面上的位置，z轴表示地面的高度。

通过调整x、y和z的数值，我们可以创建出各种形状和复杂度的三维表面。

Matlab还在其图形库中提供了许多其他类型的3D图形绘制函数。

例如，“bar3”函数可以用来绘制三维柱状图，其中x和y轴表示不同的类别，z轴表示各类别的数值。

这种图形可以更直观地展示不同类别之间的关系和差异。

类似地，“contour”函数可以用来绘制三维的等值线图，用于可视化函数的等值线和等高面。

另一个值得一提的技术是使用Matlab的“patch”函数绘制复杂的三维图形。

这个函数可以用来创建和修改三维物体的表面，例如绘制球体、立方体和多面体等。

我们可以通过更改物体的属性和位置来构建各种形状和几何体。

这种灵活性使得“patch”函数在计算机图形学和动画领域中得到广泛应用。

除了这些函数和工具，Matlab还允许用户通过编写自定义的脚本和函数来实现更高级的3D图形绘制。

例如，我们可以使用Matlab的3D绘图工具箱中的一些高级函数和方法来创建特定类型的三维图形，如体积渲染、光线追踪和动画效果等。

MATLAB绘制空间曲面的命令一、介绍在科学计算和工程领域中，经常需要对空间曲面进行可视化分析。

MATLAB作为一种强大的数值计算软件，提供了丰富的绘图函数和命令，可以轻松地绘制空间曲面。

本文将介绍MATLAB中常用的绘制空间曲面的命令，并通过示例代码详细说明其使用方法和效果。

二、绘制三维曲面1. meshgrid函数在绘制空间曲面之前，我们需要先创建一个网格。

MATLAB中的meshgrid函数可以用来生成二维或三维的坐标网格，为后续的曲面绘制提供基础。

示例代码：[x, y] = meshgrid(-10:0.5:10, -10:0.5:10);2. 曲面方程在绘制空间曲面时，我们需要定义一个曲面方程。

曲面方程可以是一个显式方程，也可以是一个隐式方程。

示例代码：z = x.^2 + y.^2;3. surf函数一旦我们定义了曲面方程和坐标网格，就可以使用surf函数来绘制空间曲面了。

surf函数可以根据给定的坐标网格和曲面方程，生成一个三维曲面图。

示例代码：surf(x, y, z);4. 其他参数设置除了基本的绘图命令外，还可以通过设置其他参数来调整曲面的外观和显示效果。

例如，可以设置曲面的颜色、透明度、光照等。

示例代码：surf(x, y, z, 'FaceColor', 'interp', 'EdgeColor', 'none');light('Position', [1 1 1]);三、绘制特殊曲面1. 球面球面是一种常见的空间曲面，可以通过给定球心和半径来定义。

MATLAB中的sphere函数可以绘制球面。

示例代码：[x, y, z] = sphere;surf(x, y, z);2. 圆柱面圆柱面是由平行于一个固定直线的所有直线和平行于一个固定平面的所有直线形成的曲面。

MATLAB中的cylinder函数可以绘制圆柱面。