安徽省六安市第一中学2015-2016学年高一下学期期中考试数学试题 Word版含答案

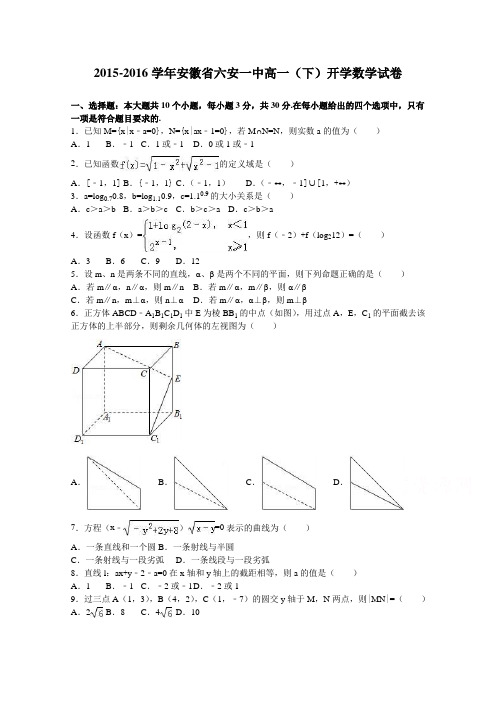
2015-2016学年安徽省六安一中高一（下）开学数学试卷一、选择题：本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知M={x|x﹣a=0}，N={x|ax﹣1=0}，若M∩N=N，则实数a的值为（）A．1 B．﹣1 C．1或﹣1 D．0或1或﹣12．已知函数的定义域是（）A．[﹣1，1] B．{﹣1，1} C．（﹣1，1）D．（﹣∞，﹣1]∪[1，+∞）3．a=log0.70.8，b=log1.10.9，c=1.10.9的大小关系是（）A．c＞a＞b B．a＞b＞c C．b＞c＞a D．c＞b＞a4．设函数f（x）=，则f（﹣2）+f（log212）=（）A．3 B．6 C．9 D．125．设m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（）A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥βC．若m∥n，m⊥α，则n⊥αD．若m∥α，α⊥β，则m⊥β6．正方体ABCD﹣A1B1C1D1中E为棱BB1的中点（如图），用过点A，E，C1的平面截去该正方体的上半部分，则剩余几何体的左视图为（）A．B．C．D．7．方程（x﹣）=0表示的曲线为（）A．一条直线和一个圆 B．一条射线与半圆C．一条射线与一段劣弧D．一条线段与一段劣弧8．直线l：ax+y﹣2﹣a=0在x轴和y轴上的截距相等，则a的值是（）A．1 B．﹣1 C．﹣2或﹣1 D．﹣2或19．过三点A（1，3），B（4，2），C（1，﹣7）的圆交y轴于M，N两点，则|MN|=（）A．2B．8 C．4D．1010．对于平面直角坐标系内任意两点A（x1，y1），B（x2，y2），定义它们之间的一种“折线距离”：d（A，B）=|x2﹣x1|+|y2﹣y1|．则下列命题正确的是（）①若A（﹣1，3），B（1，0），则；②若A为定点，B为动点，且满足d（A，B）=1，则B点的轨迹是一个圆；③若点C在线段AB上，则d（A，C）+d（C，B）=d（A，B）．A．①②B．②C．③D．①②③二、填空题（每题4分，满分16分，将答案填在答题纸上）11．若函数f（x）=xln（x+）为偶函数，则a=．12．设函数f（x）=，则函数的零点个数为个．13．在长方体ABCD﹣A1B1C1D1中，M、N分别是棱BB1、B1C1的中点，若∠CMN=90°，则异面直线AD1与DM所成的角为．14．求函数的最小值为．三、解答题（本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤.）15．已知点A（﹣3，﹣1）和点B（5，5）．（Ⅰ）求过点A且与直线AB垂直的直线l的一般式方程；（Ⅱ）求以线段AB为直径的圆C的标准方程．16．已知函数f（x）对一切实数x，y都有f（x+y）﹣f（y）=x（x+2y+1）成立，且f（1）=0．（1）求f（0）；（2）求f（x）的解析式；（3）当x∈[0，]时，f（x+3）＜2x+a恒成立，求a的范围．17．如图，直三棱柱ABC﹣A′B′C′，∠BAC=90°，，AA′=1，点M，N分别为A′B 和B′C′的中点．（Ⅰ）证明：MN∥平面A′ACC′；（Ⅱ）求三棱锥A′﹣MNC的体积．（椎体体积公式V=Sh，其中S为底面面积，h为高）18．如图，在四棱锥P﹣ABCD中，PA⊥ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．（1）证明BE⊥DC；（2）求二面角E﹣AB﹣P的值；（3）求直线BE与平面PBD所成角的正弦值．19．设直线l1：y=k1x+1，l2：y=k2x﹣1，其中实数k1，k2满足k1k2+1=0．（1）证明：直线l1与l2相交；（2）试用解析几何的方法证明：直线l1与l2的交点到原点距离为定值；（3）设原点到l1与l2的距离分别为d1和d2，求d1+d2的最大值．2015-2016学年安徽省六安一中高一（下）开学数学试卷参考答案与试题解析一、选择题：本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知M={x|x﹣a=0}，N={x|ax﹣1=0}，若M∩N=N，则实数a的值为（）A．1 B．﹣1 C．1或﹣1 D．0或1或﹣1【考点】交集及其运算．【分析】根据题意，M={a}，若M∩N=N，则N⊆M，对N是不是空集进行分2种情况讨论，分别求出符合条件的a的值，综合可得答案．【解答】解：根据题意，分析可得，M是x﹣a=0的解集，而x﹣a=0⇒x=a；故M={a}，若M∩N=N，则N⊆M，①N=∅，则a=0；②N≠∅，则有N={}，必有=a，解可得，a=±1；综合可得，a=0，1，﹣1；故选D．2．已知函数的定义域是（）A．[﹣1，1] B．{﹣1，1} C．（﹣1，1）D．（﹣∞，﹣1]∪[1，+∞）【考点】函数的定义域及其求法．【分析】由函数解析式可得，通过解不等式组可得x的范围，即得函数的定义域．【解答】解：∵，∴，∴1≤x2≤1∴x2=1即x=±1∴函数的定义域为：{﹣1，1}故选B3．a=log0.70.8，b=log1.10.9，c=1.10.9的大小关系是（）A．c＞a＞b B．a＞b＞c C．b＞c＞a D．c＞b＞a【考点】指数函数的图象与性质．【分析】由指数函数，对数函数的单调性，确定0＜a=log0.70.8＜1，b=log1.10.9＜0，c=1.10.9＞1．【解答】解：0＜a=log0.70.8＜1，b=log1.10.9＜0，c=1.10.9＞1．故选A．4．设函数f（x）=，则f（﹣2）+f（log212）=（）A．3 B．6 C．9 D．12【考点】函数的值．【分析】先求f（﹣2）=1+log2（2+2）=1+2=3，再由对数恒等式，求得f（log212）=6，进而得到所求和．【解答】解：函数f（x）=，即有f（﹣2）=1+log2（2+2）=1+2=3，f（log212）==12×=6，则有f（﹣2）+f（log212）=3+6=9．故选C．5．设m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（）A．若m∥α，n∥α，则m∥n B．若m∥α，m∥β，则α∥βC．若m∥n，m⊥α，则n⊥αD．若m∥α，α⊥β，则m⊥β【考点】空间中直线与平面之间的位置关系；空间中直线与直线之间的位置关系；平面与平面之间的位置关系．【分析】用直线与平面平行的性质定理判断A的正误；用直线与平面平行的性质定理判断B 的正误；用线面垂直的判定定理判断C的正误；通过面面垂直的判定定理进行判断D的正误．【解答】解：A、m∥α，n∥α，则m∥n，m与n可能相交也可能异面，所以A不正确；B、m∥α，m∥β，则α∥β，还有α与β可能相交，所以B不正确；C、m∥n，m⊥α，则n⊥α，满足直线与平面垂直的性质定理，故C正确．D、m∥α，α⊥β，则m⊥β，也可能m∥β，也可能m∩β=A，所以D不正确；故选C．6．正方体ABCD﹣A1B1C1D1中E为棱BB1的中点（如图），用过点A，E，C1的平面截去该正方体的上半部分，则剩余几何体的左视图为（）A．B．C．D．【考点】简单空间图形的三视图．【分析】根据剩余几何体的直观图即可得到平面的左视图．【解答】解：过点A，E，C1的平面截去该正方体的上半部分后，剩余部分的直观图如图：则该几何体的左视图为C．故选：C．7．方程（x﹣）=0表示的曲线为（）A．一条直线和一个圆 B．一条射线与半圆C．一条射线与一段劣弧D．一条线段与一段劣弧【考点】曲线与方程．【分析】根据（x﹣）=0，可得x=或=0，从而可得结论．【解答】解：∵（x﹣）=0，∴x=或=0（﹣2≤y≤4），∴x2+（y﹣1）2=9（x≥0）或x=y（﹣2≤y≤4）．故选D．8．直线l：ax+y﹣2﹣a=0在x轴和y轴上的截距相等，则a的值是（）A．1 B．﹣1 C．﹣2或﹣1 D．﹣2或1【考点】直线的截距式方程．【分析】先求出直线在两个坐标轴上的截距，由在两个坐标轴上的截距相等解方程求得a的值．【解答】解：由直线的方程：ax+y﹣2﹣a=0得，此直线在x轴和y轴上的截距分别为和2+a，由=2+a，得a=1 或a=﹣2，故选D．9．过三点A（1，3），B（4，2），C（1，﹣7）的圆交y轴于M，N两点，则|MN|=（）A．2B．8 C．4D．10【考点】两点间的距离公式．【分析】设圆的方程为x2+y2+Dx+Ey+F=0，代入点的坐标，求出D，E，F，令x=0，即可得出结论．【解答】解：设圆的方程为x2+y2+Dx+Ey+F=0，则，∴D=﹣2，E=4，F=﹣20，∴x2+y2﹣2x+4y﹣20=0，令x=0，可得y2+4y﹣20=0，∴y=﹣2±2，∴|MN|=4．故选：C．10．对于平面直角坐标系内任意两点A（x1，y1），B（x2，y2），定义它们之间的一种“折线距离”：d（A，B）=|x2﹣x1|+|y2﹣y1|．则下列命题正确的是（）①若A（﹣1，3），B（1，0），则；②若A为定点，B为动点，且满足d（A，B）=1，则B点的轨迹是一个圆；③若点C在线段AB上，则d（A，C）+d（C，B）=d（A，B）．A．①②B．②C．③D．①②③【考点】命题的真假判断与应用．【分析】利用“折线距离”：d（A，B）=|x2﹣x1|+|y2﹣y1|，逐一判断命题①②③即可得到答案．【解答】解：①∵A（﹣1，3），B（1，0），则d（A，B）=|1﹣（﹣1）|+|0﹣3|=2+5=5，故①错误；②不妨令点A为坐标原点，B（x，y），则d（A，B）=|x|+|y|=1，B点的轨迹是一个正方形，而不是圆，故②错误；③设直角坐标平面内的任意两点A（x1，y1），B（x2，y2），设C点坐标为（x0，y0），∵点C在线段AB上，∴x0在x1、x2之间，y0在y1、y2之间，不妨令x1＜x0＜x2，y1＜y0＜y2，则d（A，C）+d（C，B）=|x0﹣x1|+|y0﹣y1|+|x2﹣x0|+|y2﹣y0|=x0﹣x1+y0﹣y1+x2﹣x0+y2﹣y0=x2﹣x1+y2﹣y1=|x2﹣x1|+|y2﹣y1|=d（A，B）成立，故③正确．∴正确的命题是③．故选：C．二、填空题（每题4分，满分16分，将答案填在答题纸上）11．若函数f（x）=xln（x+）为偶函数，则a=1．【考点】函数奇偶性的性质．【分析】由题意可得，f（﹣x）=f（x），代入根据对数的运算性质即可求解．【解答】解：∵f（x）=xln（x+）为偶函数，∴f（﹣x）=f（x），∴（﹣x）ln（﹣x+）=xln（x+），∴﹣ln（﹣x+）=ln（x+），∴ln（﹣x+）+ln（x+）=0，∴ln（+x）（﹣x）=0，∴lna=0，∴a=1．故答案为：1．12．设函数f（x）=，则函数的零点个数为3个．【考点】函数零点的判定定理．【分析】问题等价于函数y=f（x）与函数y=﹣图象的公共点个数，作出函数的图象可得．【解答】解：函数的零点个数等价于函数y=f（x）与函数y=﹣图象的公共点个数，作出它们的图象可得公共点个数为3，故答案为：313．在长方体ABCD﹣A1B1C1D1中，M、N分别是棱BB1、B1C1的中点，若∠CMN=90°，则异面直线AD1与DM所成的角为90°．【考点】异面直线及其所成的角．【分析】先连BC1，则BC1∥AD1，则异面直线AD1与DM所成的角转化为直线BC1与DM 所成的角．结合M、N分别是棱BB1、B1C1的中点及三垂线定理得出直线BC1与DM所成的角90°，从而求得异面直线AD1与DM所成的角．【解答】解：连BC1，则BC1∥AD1则异面直线AD1与DM所成的角为直线BC1与DM所成的角．∵M、N分别是棱BB1、B1C1的中点∴BC1∥MN，∵∠CMN=90°，∴直线BC1⊥MC，又MC是斜线DM在平面BCC1B1上的射影，∴DM⊥BC1，直线BC1与DM所成的角90°，则异面直线AD1与DM所成的角为90°．故答案为：90°．14．求函数的最小值为5．【考点】函数的最值及其几何意义．【分析】根据其几何意义即可求出答案．【解答】解：函数=+=+表示x轴上动点P（x，0）到A（4，1）和B（0，﹣2）的距离和，当P为AB与x轴的交点时，函数取最小值|AB|==5，故答案为：5三、解答题（本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤.）15．已知点A（﹣3，﹣1）和点B（5，5）．（Ⅰ）求过点A且与直线AB垂直的直线l的一般式方程；（Ⅱ）求以线段AB为直径的圆C的标准方程．【考点】圆的标准方程．【分析】（Ⅰ）求出过点A且与直线AB垂直的直线l的斜率，根据点斜式得直线l的方程，整理得直线l的一般式方程；（Ⅱ）确定圆心坐标与半径，即可求以线段AB为直径的圆C的标准方程．【解答】解：（Ⅰ）由条件知，则根据点斜式得直线l的方程为，整理得直线l的一般式方程为4x+3y+15=0．…（Ⅱ）由题意得C（1，2），故以线段AB为直径的圆C的标准方程为（x﹣1）2+（y﹣2）2=25．…16．已知函数f（x）对一切实数x，y都有f（x+y）﹣f（y）=x（x+2y+1）成立，且f（1）=0．（1）求f（0）；（2）求f（x）的解析式；（3）当x∈[0，]时，f（x+3）＜2x+a恒成立，求a的范围．【考点】抽象函数及其应用．【分析】（1）令x=1，y=0得f（0）的方程，解方程即可得出；（2）y=0，可得f（x）的方程，即可解出f（x）的解析式；（3）f（x+3）＜2x+a可化为a＞x2+5x在x∈[0，]恒成立，转化为a＞（x2+5x）max，求最值即可．【解答】解：（1）令x=1，y=0得f（1+0）﹣f（0）=2，又f（1）=0，可得f（0）=﹣2，（2）令y=0，可得f （x ）﹣f （0）=x （x +1），所以f （x ）=x 2+x ﹣2，（3）x ∈[0，]时，f （x +3）＜2x +a 恒成立，即x ∈[0，]时，a ＞x 2+5x +10恒成立． ∴a ＞（x 2+5x +10）max ，因为x 2+5x +10在[0，]单调增，所以最大值为．所以a 的范围是a ＞．17．如图，直三棱柱ABC ﹣A ′B ′C ′，∠BAC=90°，，AA ′=1，点M ，N 分别为A ′B和B ′C ′的中点．（Ⅰ）证明：MN ∥平面A ′ACC ′；（Ⅱ）求三棱锥A ′﹣MNC 的体积．（椎体体积公式V=Sh ，其中S 为底面面积，h 为高）【考点】直线与平面平行的判定；棱柱的结构特征；棱柱、棱锥、棱台的体积．【分析】（Ⅰ）证法一，连接AB ′，AC ′，通过证明MN ∥AC ′证明MN ∥平面A ′ACC ′．证法二，通过证出MP ∥AA ′，PN ∥A ′C ′．证出MP ∥平面A ′ACC ′，PN ∥平面A ′ACC ′，即能证明平面MPN ∥平面A ′ACC ′后证明MN ∥平面A ′ACC ′．（Ⅱ）解法一，连接BN ，则V A ′﹣MNC =V N ﹣A ′MC =V N ﹣A ′BC =V A ′﹣NBC =．解法二，V A ′﹣MNC =V A ′﹣NBC ﹣V M ﹣NBC =V A ′﹣NBC =．【解答】（Ⅰ）（证法一）连接AB ′，AC ′，由已知∠BAC=90°，AB=AC ，三棱柱ABC ﹣A ′B ′C ′为直三棱柱，所以M 为AB ′的中点，又因为N 为B ′C ′中点，所以MN ∥AC ′，又MN ⊄平面A ′ACC ′，AC ′⊂平面A ′ACC ′，所以MN ∥平面A ′ACC ′；（证法二）取A ′B ′中点，连接MP ，NP ．而M ，N 分别为AB ′，B ′C ′中点，所以MP ∥AA ′，PN ∥A ′C ′．所以MP ∥平面A ′ACC ′，PN ∥平面A ′ACC ′；又MP ∩PN=P ，所以平面MPN ∥平面A ′ACC ′，而MN ⊂平面MPN ，所以MN ∥平面A ′ACC ′；（Ⅱ）（解法一）连接BN ，由题意A ′N ⊥B ′C ′，平面A ′B ′C ′∩平面B ′BCC ′=B ′C ′，所以A ′N ⊥平面NBC ，又A ′N=B ′C ′=1，故V A ′﹣MNC =V N ﹣A ′MC =V N ﹣A ′BC =V A ′﹣NBC =．（解法二）V A ′﹣MNC =V A ′﹣NBC ﹣V M ﹣NBC =V A ′﹣NBC =．18．如图，在四棱锥P ﹣ABCD 中，PA ⊥ABCD ，AD ⊥AB ，AB ∥DC ，AD=DC=AP=2，AB=1，点E 为棱PC 的中点．（1）证明BE ⊥DC ；（2）求二面角E ﹣AB ﹣P 的值；（3）求直线BE 与平面PBD 所成角的正弦值．【考点】直线与平面所成的角；空间中直线与直线之间的位置关系；二面角的平面角及求法．【分析】（1）如图所示，建立空间直角坐标系，只要证明=0，即可得出⊥．（2）设平面ABE 的法向量为=（x ，y ，z ），利用，可得取，取平面PAB 的法向量为=（1，0，0），设二面角E ﹣AB ﹣P 的平面角为θ，利用cos =即可得出．（3）=（﹣2，﹣1，0），=（0，﹣1，2），设平面PBD 的法向量为=（x ，y ，z ），利用，即可得出，设直线BE 与平面PBD 所成角的为α，利用sin α=|cos |=即可得出．【解答】（1）证明：如图所示，建立空间直角坐标系，A （0，0，0），B （0，1，0），P （0，0，2），C （﹣2，2，0），D （﹣2，0，0），E （﹣1，1，1），∴=（﹣1，0，1），=（0，2，0），∴=0，∴⊥，∴BE ⊥DC ．（2）解： =（0，1，0），设平面ABE 的法向量为=（x ，y ，z ），则，即，取=（1，0，1），取平面PAB 的法向量为=（1，0，0），设二面角E ﹣AB ﹣P 的平面角为θ，cos ===，由图可知：二面角E ﹣AB ﹣P 的平面角θ为锐角， ∴．（3）解： =（﹣2，﹣1，0），=（0，﹣1，2），设平面PBD 的法向量为=（x ，y ，z ），则，化为，取=（1，﹣2，﹣1），设直线BE 与平面PBD 所成角的为α，则sin α=|cos |===．19．设直线l1：y=k1x+1，l2：y=k2x﹣1，其中实数k1，k2满足k1k2+1=0．（1）证明：直线l1与l2相交；（2）试用解析几何的方法证明：直线l1与l2的交点到原点距离为定值；（3）设原点到l1与l2的距离分别为d1和d2，求d1+d2的最大值．【考点】过两条直线交点的直线系方程．【分析】（1）假设l1与l2平行，有k1=k2，代入k1k2+1=0，得k12+1=0，这与k1为实数的事实相矛盾，故l1与l2相交．（2）由（1）知k1≠k2，联立方程组求得交点坐标，然后由两点间的距离公式求得直线l1与l2的交点到原点距离为定值；（3）利用点到直线的距离和不等式的性质进行解答．【解答】证明：（1）反证法：假设l1与l2不相交，则l1与l2平行，有k1=k2，代入k1k2+1=0，得k12+1=0，这与k1为实数的事实相矛盾，∴k1≠k2，故l1与l2相交．（2）由（1）知k1≠k2，由方程组解得交点P的坐标（x，y）为，而x2+y2=+===1．即l1与l2的交点到原点距离为1．解：（3）d1+d2=+=+=+====，当|k1|=1即k1=±1时，d1+d2的最大值是．2016年11月2日。

安徽省六安市第一中学2015-2016学年高一数学下学期周末统测试卷（十一）（含解析）一、选择题（本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.） 1.下列各式中，值为3的是（ ） A ．2sin15cos15︒︒ B ．22cos 15sin 15︒-︒ C ．22sin 15cos 15︒-︒ D ．22sin 15cos 15︒+︒ 【答案】B 【解析】考点：二倍角及同角三角函数的基本公式. 2.,2a ππ⎛⎫∈ ⎪⎝⎭，且5cos 224παα⎛⎫=- ⎪⎝⎭，则tan α等于（ ） A ．43-B ．13-C ．34- D ．3-【答案】A 【解析】 试题分析：由5cos 224παα⎛⎫=- ⎪⎝⎭可得()()5cos sin cos sin cos sin αααααα-+=-，所以1cos sin 5αα+=，又因为,2a ππ⎛⎫∈ ⎪⎝⎭，可解得434sin ,cos ,tan 553ααα==-=-，故选A.考点：二倍角角公式及两角和的正弦公式. 3.设,αβ为钝角，且5310sin αβ==，则αβ+的值为 （ ）A ．34π B ．54π C ．74π D ．54π或74π 【答案】C 【解析】考点：已知三角函数值求角. 4.函数()tan 1cos xf x x=-+的奇偶性是（ ）A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．既不是奇函数又不是偶函数 【答案】A 【解析】试题分析：因为()2tan tan 1cos 2cos2x xf x x x =-=-+， ()()f x f x -=-，所以()f x 为奇函数，故选A.考点：三角恒等变换与函数的性质. 5.式子()22112cos 2sin R θθθ+∈--的最小值为（ ）A ．34B ．32C ．43D ．23【答案】C 【解析】 试题分析：()()22222222112sin 2cos 32cos 2sin 2sin cos 2cos 2sin θθθθθθθθ-+-+==--+--≥2223sin cos 22θθ⎛⎫++ ⎪⎝⎭43=，故选C.考点：同角三角函数的基本关系式与重要不等式.6.在ABC ∆中，35sin ,cos 513A B ==，则cos C =（ ） A ．1665或5665 B ．1665-或5665- C ．1665-D ．1665【答案】D 【解析】考点：同角三角函数基本关系及两角和的余弦. 7.若cos 22sin 4απα=-⎛⎫- ⎪⎝⎭，则cos sin αα+的值为（ ） A．．12- C ．12 D【答案】C 【解析】 试题分析：由cos 22sin 4απα=-⎛⎫- ⎪⎝⎭可得)()22cos sin cos sin cos sin sin cos sin coscos sin44ααααααππαααα-+-=--)cos sin 2αα=+=-，所以1cos sin 2αα+=，故选C. 考点：二倍角公式与两角差的正弦公式.8.设1,cos 2a θ⎛⎫=⎪⎝⎭与()1,2cos b θ=-垂直，则cos2θ的值等于（ ） A ．22-B ．12- C ．0 D ．1- 【答案】B 【解析】9.若1sin 63πθ⎛⎫-= ⎪⎝⎭，则2cos 23πθ⎛⎫+ ⎪⎝⎭的值为（ ） A ．13 B ．13- C ．79 D ．79- 【答案】D 【解析】 试题分析：由1sin 63πθ⎛⎫-= ⎪⎝⎭可得1cos 33πθ⎛⎫+= ⎪⎝⎭，所以222cos 22cos 11339ππθθ⎛⎫⎛⎫+=+-=- ⎪ ⎪⎝⎭⎝⎭79=-，故选D.考点：二倍角公式与诱导公式.【方法点晴】本题主要考查了二倍角公式与诱导公式，考查了三角求值，属于中档题.本题属于给值求值的问题，要注意探求已知条件中的角与待求值角的关系，从中找到解题思路.本题中，22326πππθ=2θ⎡⎤⎛⎫+-- ⎪⎢⎥⎝⎭⎣⎦，据此可通过诱导公式求得1cos 33πθ⎛⎫+= ⎪⎝⎭，再利用二倍角公式即可求得所求的值.10.已知点()()()()1,1,1,2,2,1,3,4A B C D ---，则向量AB 在CD 方向上的投影为（ ）A ．2 B ．2 C ．2- D ．2-【答案】A 【解析】试题分析：()()2,1,5,5AB CD ==,所以向量AB 在CD 方向上的投影为cos ,AB CD AB AB CD CD⋅=2==,故选A. 考点：向量在轴上的正投影.【方法点晴】本题主要考查了向量在轴上的正投影，属于基础题.本题解答的关键是根据向量在轴上的正投影的定义及平面向量数量积的定义，用向量的数量积和向量的模把向量AB 在CD 方向上的投影表示cos ,AB CD AB AB CDCD⋅=的形式，通过求向量,AB CD 的坐标即可求得结果，注意向量的坐标是终点坐标减去起点坐标.第Ⅱ卷（非选择题共70分）二、填空题（本大题共4小题，每题4分，满分16分．） 11.若11sin cos ,cos sin 22αβαβ-=--=, 则()sin αβ+= ． 【答案】34【解析】12.sin 47sin17cos30cos17︒-︒︒=︒ ．【答案】12【解析】 试题分析：()sin 1730sin17cos30sin 47sin17cos30cos17cos17+︒-︒︒︒-︒︒=︒︒cos17sin 301sin 30cos172︒︒==︒=︒. 考点：化简求值与两角和的正弦公式.13.设当x θ=时，函数()sin 2cos f x x x =-取得最大值，则cos θ= ．【答案】255- 【解析】14.给定两个长度为1的平面向量OA 和OB ，它们的夹角为120︒，如图所示，点C 在以O 为圆心的圆弧AB 上变动，若OC xOA yOB =+，其中,x y R ∈，则x y +的最大值是 ．【答案】2 【解析】试题分析：因为平面向量OA 和OB 的的长度都为1，且夹角为120︒，所以12OA OB ⋅=-,由OC xOA yOB=+可得()2222222221OC xOA yOBx OA y OB xyOA OB x y xy =+=++⋅=+-=，所以()()()22222231324x y x y x y xy x y xy x y ++⎛⎫+-=+-=≥+-⨯=⎪⎝⎭，解得2x y +≤，所以x y +的最大值是2.考点：向量在平面几何中的应用.【方法点晴】本题主要考查了向量在平面几何中的应用，考查了利用重要不等式求最值问题，属于中档题.本题解答的关键是把OC xOA yOB =+两边平方，利用平面向量数量积的性质得到221x y xy +-=，根据基本不等式22a b ab +⎛⎫≤ ⎪⎝⎭把上式转化为关于x y +的一元二次不等式，通过解不等式即可求得其最大值.三、解答题（本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤.） 15.计算（1）已知2sin cos 0αα-=，求sin cos sin cos sin cos sin cos αααααααα-+++-的值；（24cos 102sin10︒-︒的值. 【答案】（1）103-；（2）4. 【解析】考点：三角函数的化简、求值. 16.已知函数()22cos2sin f x x x =+.（1）求3f π⎛⎫⎪⎝⎭的值； （2）求()f x 的最大值和最小值. 【答案】（1）14-；（2）()f x 的最大值和最小值分别为2,1. 【解析】考点：二倍角的余弦公式及三角函数的值域.17.已知 ()()cos ,sin ,cos ,sin ,0a b ααβββαπ==<<<. （1）若2a b -=，求证：a b ⊥；（2）设()0,1c =，若a b c +=，求,αβ的值. 【答案】（1）证明见解析；（2）5,66ππαβ==. 【解析】试题分析：（1）把2a b -=平方可得2222a a b b -⋅+=，由于22221a b a b ====，所以0a b ⋅=.从而证得a b ⊥；（2）由a b c +=可得cos cos 0sin sin 1αβαβ+=⎧⎨+=⎩，由0βαπ<<<得0αβπ<-<，整理得1sin sin 2αβ==，结合范围即可求得,αβ的值. 试题解析：（1）证明：由题意得22a b -=，即()22222a b a a b b -=-+=，又因为22221a b a b ====所以222a b -=，即0a b =.故a b ⊥.（2）因为()()cos cos ,sin sin 0,1a b αβαβ+=++=，所以cos cos 0sin sin 1αβαβ+=⎧⎨+=⎩由此得cos cos()απβ=-，由 0βπ<<得0αβπ<-< ，又0απ<<故απβ=-代入1sin sin 2αβ==，而αβ>，所以5,66ππαβ==. 考点：平面向量垂直关系的证明及已知三角函数值求角. 18.已知函数()()4cos sin 04f x x x πωωω⎛⎫=+> ⎪⎝⎭的最小正周期为π. （1）求ω的值； （2）讨论()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的单调性. 【答案】（1）1ω=；（2）()f x 在区间0,8π⎡⎤⎢⎥⎣⎦上单调递增，在区间,82ππ⎡⎤⎢⎥⎣⎦上单调递减.【解析】试题解析：（1）()4cos sin 4cos sin cos cos sin 444f x x x x x x πππωωωωω⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭ ()()222cos sin cos 22cos sin cos x x x x x x ωωωωωω=+=+=2sin 22cos 22x x ωω++2sin 224x πω⎛⎫=++ ⎪⎝⎭，()f x 的最小正周期为π，且0ω>，从而2,12ππωω==.考点：三角恒等变换及三角函数的性质.【方法点晴】本题主要考查了三角恒等变换及三角函数的性质，属于基础题.本题解答的关键是通过两角和的正弦公式、二倍角公式等把函数()f x 化成“一角一名一次式”形式的正弦型函数，利用给出的最小正周期求得ω；对于给定区间上的单调区间可换元转化为正弦曲线由其图象求出，也可以求出其在R 上的单调区间，通过给k 取值，求出与给出的区间0,2π⎡⎤⎢⎥⎣⎦的交集来求解. 19.函数()()26cos3302xf x x ωωω=->在一个周期内的图象如图所示，A 为图象()f x的最高点,B 、C 为图象与x 轴交点，且ABC ∆为正三角形.（1）求ω的值及函数的值域；（2）若()0835f x =，且0102,33x ⎛⎫∈- ⎪⎝⎭，求()01f x +的值.【答案】（1）4πω=，()f x 的值域为23,23⎡-⎣；（2）65. 【解析】试题分析：（1）根据三角函数的恒等变换可得()233f x x πω⎛⎫=+ ⎪⎝⎭，从而求得值域，由于正三角形ABC 的高为3，求得4BC =即得周期为8，据此可得4πω=；（2）由()083f x =可得04sin 435x ππ⎛⎫+= ⎪⎝⎭，根据0102,33x ⎛⎫∈- ⎪⎝⎭求得0,4322x ππππ⎛⎫+∈- ⎪⎝⎭，03cos 435x ππ⎛⎫∴+= ⎪⎝⎭，再根据两角和的正弦公式即可求得()01f x +的值.考点：三角函数的图象与性质及三角求值.【方法点晴】本题主要考查了三角函数的图象与性质及三角求值，属于基础题.本题解得大关键是根据二倍角公式和和角公式把()f x 化成正弦型函数，得其值域，根据条件求得周期；第（2）问中求()01f x +得值时，关键是变角把0443x πππ++表示成0434x πππ⎛⎫++ ⎪⎝⎭，根据两角和的正弦公式求解，求0cos 43x ππ⎛⎫+ ⎪⎝⎭的值时，要注意对给出的范围0102,33x ⎛⎫∈- ⎪⎝⎭的应用，由此确定其符号，这也是最常见的错误.。

一、选择题（本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.在ABC ∆中，若sin ,cos A A 是关于x 的方程2320x x m -+=的两个根，则ABC ∆是（ ） A ．钝角三角形 B ．直角三角形 C ．锐角三角形 D ．不能确定 【答案】A考点：1、韦达定理；2、同角的三角基本关系式；3、三角函数的符号．2.函数()sin y A x ωϕ=+在一个周期内的图象如图所示，此函数的解析式为（ ） A ．2sin 23y x π⎛⎫=+⎪⎝⎭B ．22sin 23y x π⎛⎫=+⎪⎝⎭C ．2sin 23x y π⎛⎫=-⎪⎝⎭ D ．2sin 23y x π⎛⎫=- ⎪⎝⎭【答案】B 【解析】试题分析：由图可知152,()212122πππ==--=A T ，2ω=，又图象过 (,2)12π-2sin 2()212πϕ⎡⎤∴⨯-+=⎢⎥⎣⎦，即sin()16πϕ-+=，262ππϕπ∴-+=+k ，即 22,3πϕπ=+∈k k Z ，取21,3πϕ==k .故选B ．考点：正弦型函数的性质．3.已知非零向量12,,，e e a b 满足12122,a e e b ke e =-=+，给出以下结论： ①若1e 与2e不共线，a 与b 共线，则2k =-； ②若1e 与2e不共线，a 与b 共线，则2k =； ③存在实数k ，使得a 与b 不共线，1e 与2e共线； ④不存在实数k ，使得a 与b 不共线，1e 与2e共线.其中正确结论的个数是（ ）A ．1个B ．2个C ．3个D ．4个 【答案】B考点：共线向量定理．4.已知α为锐角，且()()()2tan 3cos 50,tan 6sin 12ππαβπαπβ⎛⎫--++=+++= ⎪⎝⎭，则sin α=（ ）A B C D ．13【答案】C 【解析】试题分析：由已知得2tan 3sin 50,tan 6sin 1,αβαβ-++=⎧⎨-=⎩tan 3α∴=，sin 3cos αα∴=，又22sin cos 1αα+=，α为锐角，sinα∴==.故选C ． 考点：1、诱导公式；2、同角的三角基本关系式．5.已知两点()()1,2,3,1A B 到直线l -l 共有（ ）条A ．1B ．2C ．3D ．4 【答案】C 【解析】试题分析：∵两点()()1,2,3,1A B ,A B -则两圆外切，有三条公切线，即为直线l ．故选C ． 考点：圆与圆的位置关系．【思路点睛】根据题意，可以分别以,A B -公切线的条数就是直线l 的条数．本题考查的是两点确定一条直线，两圆的位置关系，题中求出的数据AB =,A B 到直线l -利用数形结合进行解答更形象直观．6.已知两点()()0,3,4,0A B -，若点P 是圆2220x y y +-=上的动点，则ABP ∆面积的最小值为（ ）A ．6B ．112C ．8D ．212【答案】B考点：1、直线与圆的位置关系；2、直线的方程；3、点到直线的距离公式．7.已知(),P x y 是直线()400kx y k ++=>上一动点，,PA PB 是圆22:20C x y y +-=的两条切线，、A B 是切点，若四边形PACB 的最小面积是2，则k 的值为（ ）A ．3BC ．D ．2 【答案】D考点：1、直线与圆的位置关系；2、点到直线的距离公式． 8.函数24sin 2cos 33y x x x ππ⎛⎫=+≤≤ ⎪⎝⎭的最大值与最小值分别为（ ）A ．最大值为74，最小值为14- B ．最大值为74，最小值为2- C ．最大值为2，最小值为14- D ．最大值为2，最小值为2-【答案】B 【解析】试题分析：222sin 2cos cos 2cos 1(cos 1)2y x x x x x =+=-++=--+，433ππx ≤≤， 11cos 2∴-≤≤x ，∴当1cos 2=x 时，max 74y =，当cos 1=-x 时，min 2y =-.故选B ．考点：1、函数的基本性质；2、二次函数；3、同角的三角函数基本关系式．9.如右图，点P 在半径为1的半圆上运动，AB 是直径，当P 沿半圆弧从A 到B 运动时，点P 经过的路程x 与APB ∆的面积y 的函数()y f x =的图象是下图中的（ ）【答案】A考点：1、函数的图象与图象变化；2、正弦函数；3、三角形的面积公式． 【思路点睛】利用圆的知识可得1xPOA x ∠==，APB ∆的高为sin x ，利用三角形面积公式求解得1()2sin sin ,02f x x x x π=⨯⨯=≤≤，再根据正弦函数的图象和性质判断答案．本题考查了三角函数的图象和性质，锐角三角函数的定义，圆的性质及三角形面积的计算，结合实际问题求解，属于中档题，难度不大．10.已知函数()2log ,02sin ,2104x x f x x x π⎧<<⎪=⎨⎛⎫≤≤ ⎪⎪⎝⎭⎩，若存在实数1234,,,x x x x 满足()()()()1234f x f x f x f x ===，且1234x x x x <<<，则()()341211x x x x -⋅-⋅的取值范围是（ ）A ．()20,32B ．()9,21C ．()8,24D ．()15,25【答案】B考点：1、椭圆的定义；2、余弦定理．【思路点睛】画出函数()f x 的图象，确定121x x =，343412,210x x x x +=<<<，结合图象可知4810x <<，由此可得()()341211x x x x -⋅-⋅的取值范围．本小题主要考查分段函数的解析式求法及其图象的作法、函数的值域的应用、函数与方程的综合运用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想，属于中档题．第Ⅱ卷（非选择题共70分）二、填空题（本大题共4小题，每题5分，满分20分．）11.已知扇形的周长为10cm ，面积为42cm ，则扇形的圆心角α的弧度数为 . 【答案】12【解析】试题分析：设扇形的的半径、弧长分别为,R l ，则14,2210,Rl R l ⎧=⎪⎨⎪+=⎩解得1,8,R l =⎧⎨=⎩（舍）或4,2,R l =⎧⎨=⎩．所以答案应填：2142l R ==． 考点：１、扇形的面积；２、弧长公式． 12.已知21sin 34πα⎛⎫-= ⎪⎝⎭，则sin 3πα⎛⎫+= ⎪⎝⎭. 【答案】14-考点：诱导公式．13.已知0,2πθ⎡⎤∈⎢⎥⎣⎦，直线sin cos 10x y θθ+-=和圆()()221:1cos 4C x y θ-+-=相交所得的弦长为θ= . 【答案】6π【解析】试题分析：由题意可知圆心(1,cos )θC ，半径12R =，圆心(1,cos )θC 到直线sin cos 10x y θθ+-=的距离为2sin θθ-d ，因为0,2πθ⎡⎤∈⎢⎥⎣⎦，2sin sin θθ∴>，22sin sin sin sin d θθθθ∴=-=-，由弦长=14d =∴=，21sin sin 4θθ∴-=，即21(2sin 1)0,sin 2θθ-=∴=，6πθ∴=．所以答案应填：6π．考点：１、点到直线的距离公式；２、三角方程；3、同角的三角函数基本关系式．14.已知函数()sin 6f x x π⎛⎫=+ ⎪⎝⎭，其中,3πx a ⎡⎤∈-⎢⎥⎣⎦，若()f x 的值域是1,12⎡⎤-⎢⎥⎣⎦，则a 的取值范围是 . 【答案】,3ππ⎡⎤⎢⎥⎣⎦考点：三角函数的图象和性质． 【思路点睛】由题意可得666πππx a -≤+≤+，由()f x 的值域是1,12⎡⎤-⎢⎥⎣⎦，结合正弦函数的图象和性质得到不等式7266πππa ≤+≤是解题的关键，解不等式可得答案，属于基础知识的考查.本题考查正弦函数的定义域、值域、图象和性质和不等式的性质，考查学生分析问题、解决问题的能力以及数形结合、转化与化归的数学思想，属于基础题.15. 如图，ABC ∆是直角边等于4的等腰直角三角形，D 是斜边BC 的中点，14AM AB m AC =+⋅，向量AM的终点M 在ACD ∆的内部（不含边界），则实数m 的取值范围是 .【答案】1344m << 【解析】试题分析：如图所示，设14AE AB =，过点E 作//EP AC ，分别交,AD BC 于点,Q P ，分别过,Q P 作//,//QR AE PF AE 交AC 于,R F ．则13,,44 AR AC AF AC ==∵14AM AB m AC =+⋅，M 在ACD ∆的内部（不含边界），∴点M 在线段QP 上（不含点,Q P ），当点M 取点Q 时， 1144AM AQ AB AC ==+，可得14m =，而M 在ACD ∆的内部（不含边界），因此14m >．当点M 取点P 时，1344 AM AB AC =+，此时可得34m =，而M 在ACD ∆的内部（不含边界），因此34m <．∴1344m <<．所以答案应填：1344m <<．考点：１、向量的平行四边形法则；２、平面向量的基本定理；3、共面向量的基本定理．【思路点睛】本题考查了向量的平行四边形法则、平面向量的基本定理及其意义、共面向量的基本定理，考查了推理能力和计算能力，属于中档题．如图所示，设14AE AB =，过点E 作//EP AC ，分别交,AD BC于点,Q P ，分别过,Q P 作//,//QR AE PF AE 交AC 于,R F ．由于14AM AB m AC =+⋅，可知点M 在线段QP 上（不含点,Q P ），借助于点,Q P 即可得出m 的取值范围．三、解答题（本大题共5小题，共50分.解答应写出文字说明、证明过程或演算步骤.）16.（本小题满分10分） 已知函数()2sin 2,3f x x x R π⎛⎫=-∈ ⎪⎝⎭. （1）在给定的平面直角坐标系中，画函数()[]2sin 2,0,3f x x x ππ⎛⎫=-∈ ⎪⎝⎭的简图； （2）求()[]2sin 2,,03f x x x ππ⎛⎫=-∈- ⎪⎝⎭的单调增区间； （3）函数()3cos 2g x x =的图象只经过怎样的平移变换就可得到()2sin 2,3f x x x R π⎛⎫=-∈ ⎪⎝⎭的图 象？【答案】(1)简图见解析； (2) 7,,,01212πππ⎡⎤⎡⎤---⎢⎥⎢⎥⎣⎦⎣⎦；(3)右移512π个单位长度.(3) 将()2cos 22sin(2)2πg x x x ==+的图象右移512π个单位长度得()52sin 2()2sin(2)1223πππf x x x ⎡⎤=-+=-⎢⎥⎣⎦. 考点：1.三角函数恒等变换2.正弦型函数3.三角函数的性质4.诱导公式17.（本小题满分10分）已知圆()22:15C x y +-=，直线:10l mx y m -+-=，且直线l 与圆C 交于、A B 两点.（1）若AB =，求直线l 的倾斜角；（2）若点()1,1P 满足2AP PB = ，求此时直线l 的方程.【答案】（1）3π或23π；（2）0x y -=或20x y +-=.(2)设()()1122,1,,1A x mx m B x mx m -+-+，由题意2AP PB = 可得()()112221,1,x mx m x mx m --+=--，考点：1、直线与圆的位置关系；2、点到直线的距离公式；3、弦长公式．【思路点睛】本题主要考查直线与圆的位置关系，点到直线的距离公式，弦长公式的应用，两个向量共线的性质，两向量坐标形式的运算，属于中档题．求直线倾斜角的前提是求直线的斜率，第（1）问的关键是根据题意列出关于m 的方程解出m 的值；求直线方程的关键是求直线的斜率，前提是斜率存在，若不存在，则分类讨论，在第（2）问中求直线l 的方程即求直线AB 的方程，先要设出、A B 的坐标，由两向量共线得到两点横坐标的关系，再把直线和圆的方程联立，应用韦达定理，用m 的式子写出点A 的坐标，再代入圆的方程即得所求直线的斜率m 的值．18.（本小题满分10分）平面内有一个ABC ∆和一点O ，线段、、OA OB OC 的中点分别为、、,、、E F G BC CA AB 的中点分别为、、L M N ，设,,OA a OB b OC c === .（1）试用,,a b c 表示向量,、EL FM GN ；（2）证明线段、、EL FM GN 交于一点且互相平分.【答案】(1) ()()111,,222OE a OL b c EL OL OE b c a ==+=-=+- ，()12FM a c b =+-，()12GN a b c =+-；（2）证明见解析.考点：1、向量的三角形法则；2、向量的线性运算．【方法点睛】本题考查向量加法、数乘的几何意义，向量加法的平行四边形法则，以及向量的数乘运算，三角形中位线的性质，平行四边形的判定，平行四边形的对角线相交于一点且互相平分，考查学生逻辑推理能力，属于中档题．另一种解法：（1）()111()222 +EL EO OL OA OB OC a b c ==-++=-++；同理，()()11,22FM a c b GN a b c =+-=+- ；（2）证明：如图，连接,,,EN NL LG GE ，则//EN OB ，且12EN OB =，//GL OB ，且12GL OB =，∴//EN GL ，且EN GL =，∴四边形ENLG 为平行四边形，∴线段,EL GN 交于一点且互相平分，同理，线段,EL FM 交于一点且互相平分，∴线段、、EL FM GN 交于一点且互相平分．19.（本小题满分10分） 已知以点()2,,0C t t R t t ⎛⎫∈≠ ⎪⎝⎭为圆心的圆与x 轴交于点,O A ，与y 轴交于点,O B ，其中O 为原点. （1）当2t =时，求圆C 的方程；（2）求证：OAB ∆的面积为定值；（3）设直线24y x =-+与圆C 交于点,M N ，若OM ON =，求圆C 的方程.【答案】（1）()()22215x y -+-=；（2）证明见解析；（3）()()22215x y -+-=.(3)∵,OM ON CM CN ==，∴OC 垂直平分线段MN . ∵12,2MN OC k k =-∴=, ∴直线OC 的方程是12y x =. ∴212t t =，解得2t =或2t =-，考点：1、直线与圆的位置关系；2、点到直线的距离公式．20.（本小题满分10分）已知()22sin 22sin 261,44242f x x t x t t x ππππ⎛⎫⎛⎫⎛⎫⎡⎤=--⋅-+-+∈ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭，其最小值为()g t . （1）求()g t 的表达式；（2）当112t -≤≤时，要使关于t 的方程()g t kt =有一个实根，求实数k 的取值范围. 【答案】（1）()()225154216112821t t t g t t t t t t ⎧⎛⎫-+<-⎪ ⎪⎝⎭⎪⎪⎪⎛⎫=-+-≤≤⎨ ⎪⎝⎭⎪⎪-+>⎪⎪⎩；（2）8k ≤-或5k ≥-. 【解析】试题分析：（1）利用x 的范围确定sin 24πx ⎛⎫- ⎪⎝⎭，对函数解析式化简整理，对t 进行分类讨论，利用抛物线的性质求得每种情况的()g t 的解析式，最后综合；（2）根据（1）中获得当112t -≤≤时()g t 的解析式，令()()h x g t kt =-，要使()g t kt =有一个实根需1()2h -和(1)h 异号即可． 试题解析：(1)因为,242x ππ⎡⎤∈⎢⎥⎣⎦，所以32,464x πππ⎡⎤-∈-⎢⎥⎣⎦，所以1sin 2,142x π⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦，考点：1、三角函数的性质；2、二次函数的性质；3、函数的零点；4、分段函数．。

六安一中2015-2016学年第二学期高一年级周末作业(二）第Ⅰ卷（共30分)一、选择题:本大题共10个小题，每小题3分,共30分。

在每小题给出的四个选项中,只有一项 是符合题目要求的。

1。

点()4,2P -与圆224x y +=上任一点连线的中点轨迹方程是（ ）A ．()()22211x y -+-= B ．()()22211x y ++-= C ．()()22211x y -++=D ．()()22121x y -++=2。

过点()2,1并与两坐标轴相切的圆的方程是( ） A ．()()22111x y -+-=B ．()()22111x y -+-=或()()22555x y -+-= C ．()()22111x y -+-=或()()225525x y -+-=D ．()()22555x y -+-=3。

一条光线从点()2,3A -射出，经x 轴反射后，与圆()()22:321C x y -+-=相切，则入射光线的斜率为（ ）A ．34-B ．43-C ．34或43D ．34-或43-5。

直线y x b =+与曲线21x y =-b 的取值范围是( ）A ．||2b =B ．11b -<≤或2b =C ．21b -<≤-D ．21b -≤<-6。

若圆()()221:6C x a y b -+-=始终平分圆222:2230C x y x y +++-=的周长，则动点(),M a b 的轨迹方程是（ ）A ．222210ab a b ++++=B ．222210ab a b +--+=C ．222210ab a b +-++= D ．222210ab a b ++-+=7。

台风中心从A 地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B 在A 的正东40千米处，B 城市处于危险区总的时间约为( )小时。

A ．0.5B ．1C ．1。

5D ．2 8。

六安一中2015-2016学年第二学期高一年级周末作业（二）第Ⅰ卷（共30分）一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.点()4,2P -与圆224x y +=上任一点连线的中点轨迹方程是（ ）A ．()()22211x y -+-=B ．()()22211x y ++-= C ．()()22211x y -++= D ．()()22121x y -++= 2.过点()2,1并与两坐标轴相切的圆的方程是（ ） A ．()()22111x y -+-= B ．()()22111x y -+-=或()()22555x y -+-= C ．()()22111x y -+-=或()()225525x y -+-= D ．()()22555x y -+-=3.一条光线从点()2,3A -射出，经x 轴反射后，与圆()()22:321C x y -+-=相切，则入射光线的斜率为（ ） A ．34-B ．43-C ．34或43D ．34-或43-5.直线y x b =+与曲线x =b 的取值范围是（ ）A ．||b =B ．11b -<≤或b =．1b <≤-D ．1b ≤<-6.若圆()()221:6C x a y b -+-=始终平分圆222:2230C x y x y +++-=的周长，则动点(),M a b 的轨迹方程是（ ）A ．222210a b a b ++++= B ．222210a b a b +--+=C ．222210a b a b +-++=D ．222210a b a b ++-+=7.台风中心从A 地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B 在A 的正东40千米处，B 城市处于危险区总的时间约为（ ）小时. A ．0.5 B ．1 C ．1.5 D ．28.已知圆O 的方程为222x y +=，圆M 的方程为()()22131x y -+-=，过圆M 上任意一点P 做圆O 的切线PA ，若直线PA 与圆M 的另一个交点为Q ，则当弦PQ 的长度最大时，直线PA 的斜率k 为（ ）A ．1k =-或7k =-B ．1k =-或7k =C ．1k =或7k =-D ．1k =或7k =9.与圆22420x y y +-+=相切，并在x 轴、y 轴上的截距相等的直线共有（ ） A ．6条 B ．5条 C ．4条 D ．3条10.在平面直角坐标系中，,A B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线240x y +-=相切，则圆C 面积的最小值是（ ）A ．45π B ．34π C ．(6π- D ．54π第Ⅱ卷（共70分）二、填空题（每题4分，满分16分，将答案填在答题纸上）11.在平面直角坐标系xoy 中，若圆()2214x y +-=上存在,B A 两点关于点()1,2P 成中心对称，则直线AB 的方程为 .12.如图所示，水平地面上有一个大球，现作如下方法测量球的大小：用一个锐角为60°的三角板，斜边紧靠球面，一条直角边紧靠地面，并使三角板与地面垂直，P 为三角板与球的切点，如果测得5PA =，则球的表面积为 .13.圆221:2880C x y x y +++-=与圆222:4420C x y x y +---=的公共弦长等于 .14.已知直线():cos 2sin 1l x y θθ+-=，当θ取不同的值时，它是一系列直线123,,,l l l ⋅⋅⋅称为直线系，则下列说法正确的序号是 . ①直线系恒过定点（0,2）②直线系与圆()2221x y +-=相切 ③存在一定点不在直线系的任何直线上 ④存在四条直线围成一个正方形⑤若直线系中某三条直线围成等边三角形，则这个三角形面积是定值.三、解答题 （本大题共5小题，共54分.解答应写出文字说明、证明过程或演算步骤.） 15.(10分)已知关于,x y 的方程22:240C x y x y m +--+=. (1)若使方程C 表示圆，求m 的范围； (2)若圆C 与直线240x y +-=相切，求m .16.(10分)已知圆()()22:344C x y -+-=和直线:340l kx y k -+-=. (1)求证：不论k 取什么值，直线和圆总相交；(2)求k 取何值时，直线被圆截得的弦最短，并求出最短弦的长.17.（12分）已知圆()22:44M x y +-=，直线l 的方程为20x y -=，点P 是直线l 上一动点，过点P 作圆的切线,PA PB ，切点为,A B . (1)当P 的横坐标为165时，求APB ∠的大小； (2)求证：经过、、M A P 三点的圆N 必过定点，并求出该定点的坐标； (3)求证：直线AB 必过定点，并求出该定点的坐标. 18.(10分)已知⊙222:C x y r +=，曲线():0aE y a x=> (1)若2r =，过()2,4P -作圆的切线，求切线方程；(2)设()00,Q x y 是曲线C 与E 的一个公共点，过Q 作⊙C 的切线交x 轴、y 轴于、A B 两点，求AOB ∆的面积S (用,r a 表示).19. （12分）已知⊙O 的圆心为()2,4C 且与直线340x y -=相切，直线l 过原点且与⊙C 交于、A B 两点，P 是AB 的中点.(1)求⊙C 的方程；(2)若ABC ∆为直角三角形，求直线l ；(3)是否存在过()0,1-的直线'l ，使得'l 与l 交于Q ，对任意的直线l 有|OP ||OQ |4⋅=，若存在，求出'l ；若不存在，说明理由.六安一中2015-2016学年第二学期高一年级周末作业（二）参考答案一、选择题1-5：C C D B C 6-10:A B C D A 二、填空题11. 30x y +-= 12. 400π 13. ②③④ 三、解答题16.解：（1）圆C 恒过定点()4,3A ，而A 在圆C 上，所以不论k 取什么值，直线和圆总相交；………5分（2）1k =,弦长为…………………………………5分 17.解：（1）60°；………………4分（2）设()2,P t t ，则圆N 是以PM 为直径的圆，可得()()222244424t t t x t y +-+⎛⎫-+-=⎪⎝⎭，即()()222440x y t x y y +--+-=，由2224040x y x y y +-=⎧⇒⎨+-=⎩⊙N 过定点()840,4,,55⎛⎫⎪⎝⎭.……4分 (3)直线AB 是⊙M 与⊙N 的公共弦，即()244120x y t y +--+=，所以直线AB 恒过定点1,32⎛⎫⎪⎝⎭.……4分1,32⎛⎫⎪⎝⎭.……4分 18.解：(1)切线为2x =-或34100x y +-=.………………5分(2)切线为2220000,0,0,r r x x y y r A B x y ⎛⎫⎛⎫+=⇒ ⎪ ⎪⎝⎭⎝⎭，所以22440000111222r r r S r x y x y a=⋅==.……5分 19.解：(1) ()()22244x y -+-=.……………………3分 (2) y x =或7y x =.……………………4分(3)设直线1:':1,；k l y kx l y mx Q k m m k -⎛⎫==-⇒⎪--⎝⎭，而OP ===4⋅=，即()284140m k m ++-=对任意k （只要l 与圆C 相交）都成立，所以12m =-，即存在直线1':12l y x =--.………………5分。

高一期中考试数学试卷一、选择题：（本大题共10小题，每小题4分，共40分．每一小题给出的四个选项中只有一项是符合题目要求的．）1 ( ) A 、22sin 15cos 15︒︒+ B 、2sin15cos15︒︒C 、22cos 15sin 15︒︒- D 、22sin 151︒-2、已知向量(1,2),(5,)a b k =-=，若//a b ，则实数k 的值为 ( )A 、5B 、5-C 、10D 、10-3、数列 ,1,0,1,0,1的一个通项公式是 （ ）A 、()2111+--=n n a B 、()2111+-+=n n a C 、()211--=n na D 、()211nna ---=4、在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是（ ）A 、钝角三角形.B 、直角三角形.C 、锐角三角形.D 、不能确定.5、设tan ,tan αβ是方程2320x x -+=的两个根，则tan()αβ+的值为 ( ) A 、-3 B 、-1 C 、1 D 、36、已知平面内三点A （-1，0），B （x ，6），P （3，4），且−→−AP =λ−→−PB ，x 和λ的值分别为A 、-7，2B 、5，2C 、-7，52 D 、5，527、已知向量)3,2(=→a ，)2,1(-=→b ，若→→+b n a m 与 →→-b a 2共线，则nm等于( ) A 、21-B 、21C 、2-D 、28、函数21()cos 2f x x =-的周期为 （ ）Ａ、4π Ｂ、2πＣ、2π Ｄ、π 9、在ABC ∆中，若::1:2:3A B C ∠∠∠=，则::a b c 等于（ ）A 、1:2:3B 、3:2:1C 、D 、2 10、在ABC ∆中，有命题①=-；②=++；③若0)()(=-⋅+AC AB AC AB ，则ABC ∆ 为等腰三角形；④若0>⋅AB AC ，则ABC ∆为锐角三角形. 上述命题正确的是 （ ）BACA 、①② B、①④ C、②③ D、②③④ 二、填空题：(本大题共4小题，每小题4分，共16分．) 11、已知()*1133,21N n a a a a n n n ∈+==+，则=4a . 12、为了在一条河上建一座桥，施工前在河两岸打上两个桥位桩,A B （如图），要测算,A B 两点的距离，测量人员在岸边定出基线BC ，测得50BC m =，105,45ABC BCA ∠=∠=，就可以计算 出,A B两点的距离为 .13．在△ABC 中，||＝3，|AC |＝2，与AC 的夹角为60°，则|-AC |＝________ 14、设a 与b 为非零向量，给出下列结论：①若a 与b 平行，则a 与b 向量的方向相同或相反；②若,, AB a CD b ==a 与b 共线，则A 、B 、C 、D 四点必在一条直线上；③若a 与b 共线，则a b a b +=+；④若a 与b 反向，则a a b b=-其中正确的结论是 .（填序号）答题卡二、填空题：11、________ 12、________ 13、________ 14、________三、解答题：(本大题共5小题，共44分，解答应写出文字说明，证明过程或演算步骤．) 15、已知：→a 、→b 、→c 是同一平面内的三个向量，其中→a =（1，2） （8分） （1）若|→c |=25，且→c ‖→a，求→c 的坐标（2）若|→b |=25，且→a +2→b 与2→a -→b 垂直，求→a 与→b 的夹角的大小。

安徽省六安市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）已知双曲线两个焦点的距离为10,双曲线上任一点到两个焦点距离之差的绝对值为6,则双曲线的离心率为（）A .B .C . 1D .2. （2分） (2020高一下·南昌期中) 已知集合，，则（）A .B .C .D .3. （2分） (2020高一下·南昌期中) 在△ABC中，角A，B，C所对的边分别是a，b，c,若，则△ABC的形状是（）A . 等腰三角形B . 直角三角形C . 等腰直角三角形D . 等腰或直角三角形4. （2分） (2020高一下·南昌期中) 设成等比数列，其公比为，则的值为（）A .B .C .D . 15. （2分） (2018高二上·福建期中) 在等差数列{an}中，a3＋a9＝27－a6 ， Sn表示数列{an}的前n项和，则S11＝（）A . 18B . 99C . 198D . 2976. （2分） (2020高一下·南昌期中) 在中，，，，则的值为（）A .B .C . 或D . 或7. （2分） (2020高一下·南昌期中) 已知正实数a、b满足a+b=ab，则ab的最小值为（）A . 1B .C . 2D . 48. （2分） (2020高一下·南昌期中) 已知函数，（且）的图像恒过点，若直线经过点M，则a+b的最小值为（）A .B .C .D .9. （2分） (2020高一下·南昌期中) 有两个等差数列，，其前n项和分别为和，若，则（）A .B .C .D .10. （2分） (2020高一下·南昌期中) 已知数列，，，，，是首项为1，公比为2的等比数列，则下列项中是数列中的项是（）A . 16B . 128C . 32D . 6411. （2分） (2020高一下·南昌期中) 设等差数列的前项和，且，则满足的最大自然数n的值为（）A . 6B . 7C . 12D . 1312. （2分） (2020高一下·南昌期中) 已知数列的首项，其前n项和为，且满足，若对任意恒成立，则a的取值范围是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）已知为数列的前n项和，且，则＝________；数列的通项公式为________14. （1分） (2020高一下·南昌期中) 已知函数，则函数的最小值为________.15. （1分）(2020高一下·南昌期中) 在中, 是角所对的边长,若,则 ________．16. （1分） (2020高一下·南昌期中) 锐角中，内角的对边分别为，若，则的取值范围是________.三、解答题 (共6题；共50分)17. （10分） (2016高二上·吉安期中) 命题p：∀x∈R，ax2+ax﹣1＜0，命题q： +1＜0．（1）若“p或q”为假命题，求实数a的取值范围；（2）若“非q”是“α∈[m，m+1]”的必要不充分条件，求实数m的取值范围．18. （10分）设函数f（x）=+k（+lnx）（k为常数）．（1）当k=0时，求曲线y=f（x）在点（1，f（1））处的切线方程；（2）当k≥0时，求函数f（x）的单调区间；（3）若函数f（x）在（0，2）内存在两个极值点，求k的取值范围．19. （5分） (2019高一上·大庆期中) 已知函数（1）求函数的最小正周期、单调区间；（2）求函数在区间上的最小值和最大值.20. （10分） (2020高一下·郧县月考) 已知点，，，向量 .（1）若向量与共线，求实数的值；（2）若向量，求实数的取值范围．21. （5分） (2016高一下·赣州期中) 已知△ABC的三个内角A，B，C所对的边分别为a，b，c. ，，且．（Ⅰ）求A的大小；（Ⅱ）若a=1，．求S△ABC ．22. （10分） (2020高一下·南昌期中) 已知等差数列的前项和为，并且，，数列满足：，记数列的前n项和为 . （1）求数列的通项公式及前n项和公式；（2）求证： .参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共50分)17-1、17-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、第11 页共11 页。

2015-2016学年安徽省六安一中高一（下）期中数学试卷一、选择题：本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．在△ABC中，若sinA，cosA是关于x的方程3x2﹣2x+m=0的两个根，则△ABC是（）A．钝角三角形B．直角三角形C．锐角三角形D．不能确定2．函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（）A．y=2sin（2x+）B．y=2sin（2x+） C．y=2sin（﹣）D．y=2sin（2x﹣）3．已知非零向量，，，满足=2﹣， =k+，给出以下结论：①若与不共线，与共线，则k=﹣2；②若与不共线，与共线，则k=2；③存在实数k，使得与不共线，与共线；④不存在实数k，使得与不共线，与共线．其中正确结论的个数是（）A．1个B．2个C．3个D．4个4．已知α为锐角，且有，tan（π+α）+6sin（π+β）﹣1=0，则sinα的值是（）A．B．C．D．5．已知两点A（1，2），B（3，1）到直线l距离分别是，﹣，则满足条件的直线l共有（）条．A．1 B．2 C．3 D．46．（理科）已知两点A（0，﹣3），B（4，0），若点P是圆x2+y2﹣2y=0上的动点，则△ABP 面积的最小值为（）A．6 B．C．8 D．7．已知点P（x，y）是直线kx+y+4=0（k＞0）上一动点，PA，PB是圆C：x2+y2﹣2y=0的两条切线，A，B是切点，若四边形PACB的最小面积是2，则k的值为（）A．3 B．C． D．28．函数y=sin2x+2cosx（）的最大值与最小值分别为（）A．最大值，最小值为﹣B．最大值为，最小值为﹣2C．最大值为2，最小值为﹣D．最大值为2，最小值为﹣29．如图，点P在半径为1的半圆上运动，AB是直径，当P沿半圆弧从A到B运动时，点P 经过的路程x与△APB的面积y的函数y=f（x）的图象是下图中的（）A．B．C． D．10．已知函数f（x）=，若存在实数x1，x2，x3，x4满足f（x1）=f（x2）=f（x3）=f（x4），且x1＜x2＜x3＜x4，则的取值范围是（）A．（20，32）B．（9，21） C．（8，24） D．（15，25）二、填空题（每题4分，满分20分，将答案填在答题纸上）11．已知扇形的周长为10cm，面积为4cm2，则扇形的圆心角α的弧度数为．12．已知sin（α﹣）=，则sin（α+）= ．13．已知θ∈[0，]，直线xsinθ+ycosθ﹣1=0和圆C：（x﹣1）2+（y﹣cosθ）2=相交所得的弦长为，则θ= ．14．已知函数f（x）=sin（x+），其中x∈[﹣，α]，若f（x）的值域是[﹣，1]，则a的取值范围是．15．如图△ABC是直角边等于4的等腰直角三角形，D是斜边BC的中点， =+m•，向量的终点M在△ACD的内部（不含边界），则实数m的取值范围是．三、解答题（本大题共5小题，共50分.解答应写出文字说明、证明过程或演算步骤.）16．已知函数f（x）=2sin（2x﹣），x∈R．（1）在给定的平面直角坐标系中，画函数f（x）=2sin（2x﹣），x∈[0，π]的简图；（2）求f（x）=2sin（2x﹣），x∈[﹣π，0]的单调增区间；（3）函数g（x）=2cos2x的图象只经过怎样的平移变换就可得到f（x）=2sin（2x﹣），x∈R的图象？17．已知圆C：x2+（y﹣1）2=5，直线l：mx﹣y+1﹣m=0，且直线l与圆C交于A、B两点．（1）若|AB|=，求直线l的倾斜角；（2）若点P（1，1），满足2=，求直线l的方程．18．平面内有一个△ABC和一点O（如图），线段OA，OB，OC的中点分别为E，F，G，BC，CA，AB的中点分别为L，M，N，设=， =， =．（1）试用，，表示向量，，；（2）证明：线段EL，FM，GN交于一点且互相平分．19．已知：以点C（t，）（t∈R，t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．（Ⅰ）当t=2时，求圆C的方程；（Ⅱ）求证：△OAB的面积为定值；（Ⅲ）设直线y=﹣2x+4与圆C交于点M，N，若|OM|=|ON|，求圆C的方程．20．已知f（x）=sin2（2x﹣）﹣2t•sin（2x﹣）+t2﹣6t+1（x∈[，]）其最小值为g（t）．（1）求g（t）的表达式；（2）当﹣≤t≤1时，要使关于t的方程g（t）=kt有一个实根，求实数k的取值范围．2015-2016学年安徽省六安一中高一（下）期中数学试卷参考答案与试题解析一、选择题：本大题共10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．在△ABC中，若sinA，cosA是关于x的方程3x2﹣2x+m=0的两个根，则△ABC是（）A．钝角三角形B．直角三角形C．锐角三角形D．不能确定【考点】三角形的形状判断．【分析】根据根与系数之间的关系以及三角函数的运算公式即可得到结论．【解答】解：∵sinA，cosA是关于x的方程3x2﹣2x+m=0的两个根，∴sinA+cosA=，sinAcosA=，则平方得1+2sinAcosA=，即sinAcosA=﹣＜0，在△ABC中，sinA＞0，则cosA＜0，即A是钝角，故△ABC是钝角三角形，故选：A2．函数y=Asin（ωx+φ）在一个周期内的图象如图，此函数的解析式为（）A．y=2sin（2x+）B．y=2sin（2x+） C．y=2sin（﹣）D．y=2sin（2x﹣）【考点】由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】根据已知中函数y=Asin（ωx+ϕ）在一个周期内的图象经过（﹣，2）和（﹣，2），我们易分析出函数的最大值、最小值、周期，然后可以求出A，ω，φ值后，即可得到函数y=Asin（ωx+ϕ）的解析式．【解答】解：由已知可得函数y=Asin（ωx+ϕ）的图象经过（﹣，2）点和（﹣，2）则A=2，T=π即ω=2则函数的解析式可化为y=2sin（2x+ϕ），将（﹣，2）代入得﹣+ϕ=+2k π，k ∈Z ，即φ=+2k π，k ∈Z ，当k=0时，φ=此时故选A3．已知非零向量，，，满足=2﹣， =k +，给出以下结论：①若与不共线，与共线，则k=﹣2；②若与不共线，与共线，则k=2；③存在实数k ，使得与不共线，与共线；④不存在实数k ，使得与不共线，与共线．其中正确结论的个数是（ ） A ．1个 B ．2个 C ．3个 D ．4个【考点】命题的真假判断与应用；平行向量与共线向量．【分析】利用向量共线，列出方程，求出k 判断①②是正误；利用与共线，推出与的关系，求出k ，判断③④的正误．【解答】解：非零向量，，，满足=2﹣， =k+，与不共线，与共线，可得：λ=，即：2λ=k ，﹣λ=1，解得k=﹣2．所以①正确，②错误；与共线；可得： =m， =2﹣=（m ﹣1），=k+=（km+1），可得与共线，所以③错误，④正确． 故选：B ．4．已知α为锐角，且有，tan （π+α）+6sin （π+β）﹣1=0，则sin α的值是（ ）A．B．C．D．【考点】三角函数的化简求值．【分析】先根据诱导公式进行化简整理，然后求出tanα，最后根据同角三角函数关系求出sinα即可．【解答】解：∵，tan（π+α）+6sin（π+β）﹣1=0∴﹣2tanα+3sinβ+5=0…①tanα﹣6sinβ﹣1=0…②①×2+②得tanα=3∵α为锐角，∴sinα=故选C．5．已知两点A（1，2），B（3，1）到直线l距离分别是，﹣，则满足条件的直线l共有（）条．A．1 B．2 C．3 D．4【考点】点到直线的距离公式．【分析】A（1，2）到直线l的距离是，直线是以A为圆心，为半径的圆的切线，B（3，1）到直线l的距离﹣，直线是以B为圆心，为半径的圆的切线，满足条件的直线l是两圆公切线，由此能求出结果．【解答】解：A（1，2）到直线l的距离是，直线是以A为圆心，为半径的圆的切线，同理B（3，1）到直线l的距离﹣，直线是以B为圆心，为半径的圆的切线，∴满足条件的直线l为以A为圆心，为半径的圆和以B为圆心，为半径的圆的公切线，∵|AB|==，两个半径分别为和，∴两圆外切，∴两圆公切线有3条故满足条件的直线l有3条．故选：C．6．（理科）已知两点A（0，﹣3），B（4，0），若点P是圆x2+y2﹣2y=0上的动点，则△ABP 面积的最小值为（）A．6 B．C．8 D．【考点】圆方程的综合应用．【分析】求△ABP面积的最小值，即求P到直线AB的最小值，即为圆心到直线AB的距离减去半径．利用三角形的面积公式可得结论．【解答】解：求△ABP面积的最小值，即求P到直线AB的最小值，即为圆心到直线AB的距离减去半径．直线AB的方程为，即3x﹣4y﹣12=0，圆x2+y2﹣2y=0，即x2+（y﹣1）2=1，圆心为（0，1），半径为1∵圆心到直线AB的距离为d==，∴P到直线AB的最小值为=∵|AB|=5，∴△ABP面积的最小值为=故选B．7．已知点P（x，y）是直线kx+y+4=0（k＞0）上一动点，PA，PB是圆C：x2+y2﹣2y=0的两条切线，A，B是切点，若四边形PACB的最小面积是2，则k的值为（）A．3 B．C． D．2【考点】直线和圆的方程的应用．【分析】先求圆的半径，四边形PACB的最小面积是2，转化为三角形PBC的面积是1，求出切线长，再求PC的距离也就是圆心到直线的距离，可解k的值．【解答】解：圆C：x2+y2﹣2y=0的圆心（0，1），半径是r=1，由圆的性质知：S四边形PACB=2S△PBC，四边形PACB的最小面积是2，∴S△PBC的最小值=1=rd（d是切线长）∴d最小值=2圆心到直线的距离就是PC的最小值，∵k＞0，∴k=2故选D．8．函数y=sin2x+2cosx（）的最大值与最小值分别为（）A．最大值，最小值为﹣B．最大值为，最小值为﹣2C．最大值为2，最小值为﹣D．最大值为2，最小值为﹣2【考点】二倍角的余弦；二次函数的性质．【分析】利用同角三角函数基本关系将y解析式第一项变形，整理后配方得到关于cosx的二次函数，由x的范围求出cosx的值域，利用二次函数的性质即可求出y的最大值与最小值．【解答】解：y=sin2x+2cosx=1﹣cos2x+2cosx=﹣（cosx﹣1）2+2，∵≤x≤，∴﹣1≤cosx≤，则当cosx=时，y取得最大值，y最大为；当cosx=﹣1时，y取得最小值，y最小为﹣2．故选B9．如图，点P在半径为1的半圆上运动，AB是直径，当P沿半圆弧从A到B运动时，点P 经过的路程x与△APB的面积y的函数y=f（x）的图象是下图中的（）A．B．C． D．【考点】函数的图象与图象变化．【分析】利用圆的知识求解：∠POA==x，△APB的高为sinx，利用面积公式求解得出f（x）=sinx=sinx，0≤x≤π，判断答案．【解答】解：根据题意得出：∠POA==x，∴△APB的高为1×sinx=sinx，∵AB=2，∴△APB的面积为f（x）=sinx=sinx，0≤x≤π，∴y=f（x）的图象为A，故选：A10．已知函数f（x）=，若存在实数x1，x2，x3，x4满足f（x1）=f（x2）=f（x3）=f（x4），且x1＜x2＜x3＜x4，则的取值范围是（）A．（20，32）B．（9，21） C．（8，24） D．（15，25）【考点】函数的零点与方程根的关系．【分析】画出函数f（x）的图象，确定x1x2=1，x3+x4=12，2＜x3＜x4＜10，由此可得则的取值范围．【解答】解：函数的图象如图所示，∵f（x1）=f（x2），∴﹣log2x1=log2x2，∴log2x1x2=0，∴x1x2=1，∵f（x3）=f（x4），∴x3+x4=12，2＜x3＜x4＜10∴=x3x4﹣（x3+x4）+1=x3x4﹣11，∵2＜x3＜x4＜10∴的取值范围是（9，21）．故选：B．二、填空题（每题4分，满分20分，将答案填在答题纸上）11．已知扇形的周长为10cm，面积为4cm2，则扇形的圆心角α的弧度数为．【考点】扇形面积公式．【分析】根据题意设出扇形的弧长与半径，通过扇形的周长与面积，即可求出扇形的弧长与半径，进而根据公式α=求出扇形圆心角的弧度数．【解答】解：设扇形的弧长为：l，半径为r，所以2r+l=10，∵S扇形=lr=4，解得：r=4，l=2∴扇形的圆心角的弧度数是： =；故答案为：．12．已知sin（α﹣）=，则sin（α+）= ．【考点】两角和与差的正弦函数．【分析】利用两角差与和的正弦函数公式，特殊角的三角函数值化简已知即可得解．【解答】解：∵sin（α﹣）=﹣sinα﹣cosα=，∴﹣（sinα+cosα）=﹣sin（α+）=，∴sin（α+）=．故答案为：．13．已知θ∈[0，]，直线xsinθ+ycosθ﹣1=0和圆C：（x﹣1）2+（y﹣cosθ）2=相交所得的弦长为，则θ= ．【考点】直线与圆的位置关系．【分析】求出圆心和半径，以及圆心到直线的距离，根据直线和圆相交的弦长公式进行求解即可．【解答】解：圆的半径为R=，圆心C（1，cosθ），则圆心到直线的距离d==|sinθ+cos2θ﹣1|=|sinθ﹣sin2θ|，∵直线xsinθ+ycosθ﹣1=0和圆C：（x﹣1）2+（y﹣cosθ）2=相交所得的弦长为，等比数列R2=d2+（）2，即=（sinθ﹣sin2θ）2+，即（sinθ﹣sin2θ）2=﹣=，∵θ∈[0，]，∴sinθ﹣sin2θ=，即sin2θ﹣sinθ=，则（sinθ﹣）2=0，则sinθ=，则θ=，故答案为：，14．已知函数f（x）=sin（x+），其中x∈[﹣，α]，若f（x）的值域是[﹣，1]，则a的取值范围是[，π] ．【考点】正弦函数的图象．【分析】根据f（x）的值域，利用正弦函数的图象和性质，即可得出α+的取值范围，由此求出α的取值范围．【解答】解：∵x∈[﹣，α]时，函数f（x）=sin（x+）的值域是[﹣，1]，∴x+∈[﹣，α+]；由正弦函数的图象和性质知≤α+≤，解得≤α≤π．故答案为：[，π]．15．如图△ABC是直角边等于4的等腰直角三角形，D是斜边BC的中点， =+m•，向量的终点M在△ACD的内部（不含边界），则实数m的取值范围是（，）．【考点】向量数乘的运算及其几何意义．【分析】根据向量加法的平行四边形法则得出M的轨迹，根据条件得出m的最大值和最小值即可．【解答】解：在AB上取点D，使得，过D作DE⊥AB，交BC于E，交AD于F，∵，∴的终点M落在直线DE上．过F作FM⊥AC于M，过E作EN⊥AC于N，∴若向量的终点M在△ACD的内部（不含边界），则M必定在线段EF上（不含端点）．∵△ABC是等腰直角三角形，AB=AC=4，∴AM=1，AN=3，∴．故答案为：（，）．三、解答题（本大题共5小题，共50分.解答应写出文字说明、证明过程或演算步骤.）16．已知函数f（x）=2sin（2x﹣），x∈R．（1）在给定的平面直角坐标系中，画函数f（x）=2sin（2x﹣），x∈[0，π]的简图；（2）求f（x）=2sin（2x﹣），x∈[﹣π，0]的单调增区间；（3）函数g（x）=2cos2x的图象只经过怎样的平移变换就可得到f（x）=2sin（2x﹣），x∈R的图象？【考点】函数y=Asin（ωx+φ）的图象变换；正弦函数的图象．【分析】（1）利用五点法做函数y=Asin（ωx+φ）的在一个周期[0，π]上的图象．（2）利用正弦函数的单调性求得f（x）在x∈[﹣π，0]的单调增区间．（3）利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：（1）对于函数f（x）=2sin（2x﹣），x∈R，由x∈[0，π]，可得2x﹣∈[﹣，]，列表如下：作图：（2）令2kπ﹣≤2x﹣≤2kπ+，求得kπ﹣≤x≤kπ+，可得函数的增区间为[kπ﹣，kπ+]，k∈Z，再结合x∈[﹣π，0]，可得求f（x）=2sin（2x﹣），x∈[﹣π，0]的单调增区间为．（3）把函数g（x）=2cos2x=2sin（2x+）=2sin2（x+）的图象向右平移个单位，就可得到f（x）=2sin2（x﹣）=2sin（2x﹣）的图象．17．已知圆C：x2+（y﹣1）2=5，直线l：mx﹣y+1﹣m=0，且直线l与圆C交于A、B两点．（1）若|AB|=，求直线l的倾斜角；（2）若点P（1，1），满足2=，求直线l的方程．【考点】直线和圆的方程的应用．【分析】（1）求出弦心距、利用点到直线的距离公式可得直线的斜率，即可求直线l的倾斜角；（2）设点A（x1，mx1﹣m+1），点B（x2，mx2﹣m+1 ），由题意2=，可得2x1+x2=3．①再把直线方程 y﹣1=m（x﹣1）代入圆C，化简可得x1+x2=②，由①②解得点A的坐标，把点A的坐标代入圆C的方程求得m的值，从而求得直线L的方程．【解答】解：（1）由于半径r=，|AB|=，∴弦心距d=，再由点到直线的距离公式可得d==，解得m=±．故直线的斜率等于±，故直线的倾斜角等于或．（2）设点A（x1，mx1﹣m+1），点B（x2，mx2﹣m+1 ），由题意2=，可得 2（1﹣x1，﹣mx1+m ）=（x2﹣1，mx2﹣m ），∴2﹣2x1=x2﹣1，即2x1+x2=3．①再把直线方程 y﹣1=m（x﹣1）代入圆C：x2+（y﹣1）2=5，化简可得（1+m2）x2﹣2m2x+m2﹣5=0，由根与系数的关系可得x1+x2=②．由①②解得x1=，故点A的坐标为（，）．把点A的坐标代入圆C的方程可得m2=1，故m=±1，故直线L的方程为x﹣y=0，或x+y﹣2=0．18．平面内有一个△ABC和一点O（如图），线段OA，OB，OC的中点分别为E，F，G，BC，CA，AB的中点分别为L，M，N，设=， =， =．（1）试用，，表示向量，，；（2）证明：线段EL，FM，GN交于一点且互相平分．【考点】向量的三角形法则．【分析】（1）根据向量的加法、数乘的几何意义，以及向量加法的平行四边形法则，并进行向量的数乘运算便可得到，从而同理可以用分别表示出；（2）可连接EN，NL，LG，GE，根据三角形中位线的性质及平行四边形的定义便可得到四边形NLGE为平行四边形，从而对角线EL，GN交于一点且互相平分，而同理可证明EL，FM相交于一点且互相平分，从而便得出线段EL，FM，GN交于一点且互相平分．【解答】解：（1）=；同理，，；（2）证明：如图，连接EN，NL，LG，GE，根据条件，则：NE∥BO，且，LG∥BO，且；∴NE∥LG，且NE=LG；∴四边形NLGE为平行四边形；∴线段El，GN交于一点且互相平分；同理，线段EL，FM交于一点且互相平分；∴线段EL，FM，GN交于一点且互相平分．19．已知：以点C（t，）（t∈R，t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为原点．（Ⅰ）当t=2时，求圆C的方程；（Ⅱ）求证：△OAB的面积为定值；（Ⅲ）设直线y=﹣2x+4与圆C交于点M，N，若|OM|=|ON|，求圆C的方程．【考点】直线和圆的方程的应用．【分析】（Ⅰ）当t=2时，圆心为C（2，1），即可得出圆C的方程；（Ⅱ）求出半径，写出圆的方程，再解出A、B的坐标，表示出面积即可；（Ⅲ）设MN的中点为H，则CH⊥MN，根据C、H、O三点共线，K MN=﹣2，由直线OC的斜率k=，求得t的值，可得所求的圆C的方程．【解答】（Ⅰ）解：当t=2时，圆心为C（2，1），∴圆C的方程为（x﹣2）2+（y﹣1）2=5；（Ⅱ）证明：由题设知，圆C的方程为（x﹣t）2+（y﹣）2=t2+，化简得x2﹣2tx+y2﹣y=0．当y=0时，x=0或2t，则A（2t，0）；当x=0时，y=0或，则B（0，），∴S△AOB=OA•OB=|2t|•||=4为定值．（Ⅲ）解：∵OM=ON，则原点O在MN的中垂线上，设MN的中点为H，则CH⊥MN，∴C、H、O三点共线，K MN=﹣2，则直线OC的斜率k=，∴t=2或t=﹣2．∴圆心为C（2，1）或C（﹣2，﹣1），∴圆C的方程为（x﹣2）2+（y﹣1）2=5或（x+2）2+（y+1）2=5．由于当圆方程为（x+2）2+（y+1）2=5时，直线2x+y﹣4=0到圆心的距离d＞r，此时不满足直线与圆相交，故舍去，∴所求的圆C的方程为（x﹣2）2+（y﹣1）2=5．20．已知f （x ）=sin 2（2x ﹣）﹣2t•sin（2x ﹣）+t 2﹣6t+1（x ∈[，]）其最小值为g （t ）．（1）求g （t ）的表达式；（2）当﹣≤t≤1时，要使关于t 的方程g （t ）=kt 有一个实根，求实数k 的取值范围． 【考点】三角函数中的恒等变换应用；三角函数的最值．【分析】（1）利用x 的范围确定sin （2x ﹣），对函数解析式化简整理，对t 进行分类讨论，利用抛物线的性质求得每种情况的g （t ）的解析式，最后综合．（2）根据（1）中获得当时g （t ）的解析式，令h （t ）=g （t ）﹣kt ，要使g（t ）=kt 有一个实根需h （﹣）和h （1）异号即可．【解答】解：（1）∵x ∈[，]，∴sin （2x ﹣）∈[﹣，1]，∴f （x ）=[sin （2x ﹣﹣t]2﹣6t+1，当t ＜﹣时，则当sinx=﹣时，f （x ）min =；当﹣≤t≤1时，当sinx=t 时，f （x ）min =﹣6t+1； 当t ＞1时，当sinx=1时，f （x ）min =t 2﹣8t+2；∴g （t ）=（2）当时，g （t ）=﹣6t+1．令h （t ）=g （t ）﹣kt ．欲使g （t ）=kt 有一个实根，则只需使或即可．解得k≤﹣8或k≥﹣5．。

2015-2016学年安徽省六安市舒城中学高一（下）期中数学试卷（理科）一．选择题（本大题共12小题，每题5分，共60分）1．sin45°sin105°+sin45°sin15°=（）A．0 B．C．D．12．已知a＞b＞0，那么下列不等式成立的是（）A．﹣a＞﹣b B．a+c＜b+c C．（﹣a）2＞（﹣b）2D．3．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）．经过2个小时，这种细菌由1个可繁殖成（）A．512个B．256个C．128个D．64个4．两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（）A．akm B．akm C．2akm D．akm5．在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．若sinC+sin（B﹣A）=sin2A，则△ABC的形状为（）A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形6．已知向量=（1，），=（，x）共线，则实数x的值为（）A．1 B．C．tan35°D．tan35°7．函数f（x）=sinωx+acosωx（a＞0，ω＞0）在x=处取最小值﹣2，则ω的一个可能取值是（）A．2 B．3 C．7 D．98．数列﹣1，4，﹣7，10，…，（﹣1）n（3n﹣2）的前n项和为S n，则S11+S20=（）A．﹣16 B．14 C．28 D．309．等比数列的前n项，前2n项，前3n项的和分别为A，B，C，则（）A．B2=AC B．A+C=2B C．B（B﹣A）=A（C﹣A）D．B（B﹣A）=C（C﹣A）10．已知函数y=f（x）对任意实数x都有f（1+x）=f（1﹣x），且函数f（x）在[1，+∞）上为单调函数．若数列{a n}是公差不为0的等差数列，且f（a6）=f（a23），则{a n}的前28项之和S28=（）A．7 B．14 C．28 D．5611．若数列{a n}的通项公式a n=5（）2n﹣2﹣4（）n﹣1（n∈N*），{a n}的最大项为第p项，最小项为第q项，则q﹣p等于（）A．1 B．2 C．3 D．412．如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（，﹣），∠AOC=α，若|BC|=1，则cos2﹣sin cos﹣的值为（）A．B．C．﹣D．﹣二、填空题（本大题共4小题，每题5分，共20分）13．在数列中，则实数a=，b=．14．已知tanβ=，tan（α﹣β）=，其中α，β均为锐角，则α=．15．已知a，b是互异的负数，A是a，b的等差中项，G是a，b的等比中项，则A与G的大小关系为．16．已知数列{a n}中，2a n，a n是方程x2﹣3x+b n=0的两根，a1=2，则b5=．+1三、解答题（本大题共6小题，共70分）17．已知cos（+θ）=﹣，＜θ＜，求的值．18．已知△ABC的三边是连续的三个正整数，且最大角是最小角的2倍，求△ABC的面积．19．已知数列{a n}的前n项和S n=2n2﹣19n+1，记T n=|a1|+|a2|+…+|a n|．（1）求S n的最小值及相应n的值；（2）求T n．20．已知等差数列{a n}，等比数列{b n}满足：a1=b1=1，a2=b2，2a3﹣b3=1．（Ⅰ）求数列{a n}，{b n}的通项公式；（Ⅱ）记c n=a n b n，求数列{c n}的前n项和S n．21．已知向量=（，1），=（cos，），记f（x）=．（1）求函数f（x）的最小正周期和单调递增区间；（2）将函数y=f（x）的图象向右平移个单位得到y=g（x）的图象，讨论函数y=g（x）﹣k在的零点个数．22．已知点（1，）是函数f（x）=a x（a＞0且a≠1）的图象上一点，等比数列{a n}的前n=+项和为f（n）﹣c，数列{b n}（b n＞0）的首项为c，且前n项和S n满足S n﹣S n﹣1（n≥2）．记数列{}前n项和为T n，（1）求数列{a n}和{b n}的通项公式；（2）若对任意正整数n，当m∈[﹣1，1]时，不等式t2﹣2mt+＞T n恒成立，求实数t的取值范围（3）是否存在正整数m，n，且1＜m＜n，使得T1，T m，T n成等比数列？若存在，求出m，n的值，若不存在，说明理由．2015-2016学年安徽省六安市舒城中学高一（下）期中数学试卷（理科）参考答案与试题解析一．选择题（本大题共12小题，每题5分，共60分）1．sin45°sin105°+sin45°sin15°=（）A．0 B．C．D．1【考点】两角和与差的余弦函数；运用诱导公式化简求值．【分析】利用诱导公式，两角差的余弦函数公式，特殊角的三角函数值即可化简求值得解．【解答】解：sin45°sin105°+sin45°sin15°=cos45°cos15°+sin45°sin15°=cos（45°﹣15°）=cos30°=．故选：C．【点评】本题主要考查了诱导公式，两角差的余弦函数公式，特殊角的三角函数值在三角函数化简求值中的应用，考查了转化思想，属于基础题．2．已知a＞b＞0，那么下列不等式成立的是（）A．﹣a＞﹣b B．a+c＜b+c C．（﹣a）2＞（﹣b）2D．【考点】不等式的基本性质．【分析】由条件求得﹣a＜﹣b＜0，从而得到（﹣a）2＞（﹣b）2，从而得到结论．【解答】解：∵a＞b＞0，∴﹣a＜﹣b＜0，∴（﹣a）2＞（﹣b）2，故选C．【点评】本题主要考查不等式的基本性质的应用，属于基础题．3．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）．经过2个小时，这种细菌由1个可繁殖成（）A．512个B．256个C．128个D．64个【考点】等比数列的性质．【分析】求出经过2小时细菌分裂次数，利用有理数指数幂求解得答案．【解答】解：经过2个小时，总共分裂了=6次，则经过2小时，这种细菌能由1个繁殖到26=64个．故选：D．【点评】本题考查数列的应用，考查了等比数列的通项公式，是基础的计算题．4．两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为（）A．akm B．akm C．2akm D．akm【考点】解三角形的实际应用．【分析】先根据题意确定∠ACB的值，再由余弦定理可直接求得|AB|的值．【解答】解：根据题意，△ABC中，∠ACB=180°﹣20°﹣40°=120°，∵AC=BC=akm，∴由余弦定理，得cos120°=，解之得AB=akm，即灯塔A与灯塔B的距离为akm，故选：D．【点评】本题给出实际应用问题，求海洋上灯塔A与灯塔B的距离．着重考查了三角形内角和定理和运用余弦定理解三角形等知识，属于基础题．5．在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．若sinC+sin（B﹣A）=sin2A，则△ABC的形状为（）A．等腰三角形B．直角三角形C．等腰直角三角形D．等腰三角形或直角三角形【考点】两角和与差的正弦函数．【分析】由已知条件结合三角函数公式化简可得2cosA（sinA﹣sinB）=0，分别可得A=，或a=b，可得结论．【解答】解：∵sinC+sin（B﹣A）=sin2A，∴sin（A+B）+sin（B﹣A）=sin2A，∴sinAcosB+cosAsinB+sinBcosA﹣cosBsinA=sin2A，∴2cosAsinB=sin2A=2sinAcosA，∴2cosA（sinA﹣sinB）=0，∴cosA=0，或sinA=sinB，∴A=，或a=b，∴△ABC为等腰三角形或直角三角形故选：D．【点评】本题考查三角形形状的判断，涉及三角函数公式的应用，本题易约掉cosA而导致漏解，属中档题和易错题．6．已知向量=（1，），=（，x）共线，则实数x的值为（）A．1 B．C．tan35°D．tan35°【考点】平面向量共线（平行）的坐标表示．【分析】先根据向量的共线得到x=，再利用诱导公式和二倍角公式化简即可．【解答】解：∵向量=（1，），=（，x）共线，∴x====，故选：B．【点评】本题考查了向量的共线的条件和三角函数的化简，属于基础题．7．函数f（x）=sinωx+acosωx（a＞0，ω＞0）在x=处取最小值﹣2，则ω的一个可能取值是（）A．2 B．3 C．7 D．9【考点】正弦函数的图象；三角函数中的恒等变换应用．【分析】先根据函数的最小值求得a的值，可得函数的解析式，再利用正弦函数的图象的对称性求得ω的值．【解答】解：∵函数f（x）=sinωx+acosωx（a＞0，ω＞0）在x=处取最小值﹣2，∴sin+acos=﹣=﹣2，∴a=，∴f（x）=sinωx+cosωx=2sin（ωx+）．再根据f（）=2sin（+）=﹣2，可得+=2kπ+，k∈Z，∴ω=12k+7，∴k=0时，ω=7，则ω的可能值为7，故选：C．【点评】本题主要考查三角恒等变换，正弦函数的图象的对称性，属于基础题．8．数列﹣1，4，﹣7，10，…，（﹣1）n（3n﹣2）的前n项和为S n，则S11+S20=（）A．﹣16 B．14 C．28 D．30【考点】数列的求和．【分析】由a n=（﹣1）n（3n﹣2），利用分组求和法和等差数列求和公式能求出S11+S20．【解答】解：∵a n=（﹣1）n（3n﹣2），∴S11=（）+（a2+a4+a6+a8+a10）=﹣（1+7+13+19+25+31）+（4+10+16+22+28）=﹣16，S20=（a1+a3+…+a19）+（a2+a4+…+a20）=﹣（1+7+...+55）+（4+10+ (58)=﹣+=30，∴S11+S20=﹣16+30=14．故选：B．【点评】本题考查数列求和，是中档题，解题时要认真审题，注意分组求和法和等差数列的性质的合理运用．9．等比数列的前n项，前2n项，前3n项的和分别为A，B，C，则（）A．B2=AC B．A+C=2B C．B（B﹣A）=A（C﹣A）D．B（B﹣A）=C（C﹣A）【考点】等比数列的前n项和．【分析】讨论公比是否是1，从而分别求A，B，C，从而判断选项是否成立即可．【解答】解：若公比q=1，则B，C成立；故排除A，D；若公比q≠1，则A=S n=，B=S2n=，C=S3n=，B（B﹣A）=（﹣）=（1﹣q n）（1﹣q n）（1+q n）A（C﹣A）=（﹣）=（1﹣q n）（1﹣q n）（1+q n）；故B（B﹣A）=A（C﹣A）；故选：C．【点评】本题考查了等比数列的性质的判断与应用，同时考查了分类讨论及学生的化简运算能力．10．已知函数y=f（x）对任意实数x都有f（1+x）=f（1﹣x），且函数f（x）在[1，+∞）上为单调函数．若数列{a n}是公差不为0的等差数列，且f（a6）=f（a23），则{a n}的前28项之和S28=（）A．7 B．14 C．28 D．56【考点】数列的求和．【分析】函数y=f（x）对任意实数x都有f（1+x）=f（1﹣x），且函数f（x）在[1，+∞）上为单调函数．可得：函数f（x）关于直线x=1对称，数列{a n}是公差不为0的等差数列，且f（a6）=f（a23），可得a6+a23=2．再利用等差数列的前n项和公式即可得出．【解答】解：∵函数y=f（x）对任意实数x都有f（1+x）=f（1﹣x），且函数f（x）在[1，+∞）上为单调函数．∴函数f（x）关于直线x=1对称，∵数列{a n}是公差不为0的等差数列，且f（a6）=f（a23），∴a6+a23=2．则{a n}的前28项之和S28==14（a6+a23）=28．故选：C．【点评】本题考查了等差数列的通项公式性质及其前n项和公式、函数的对称性，考查了推理能力与计算能力，属于中档题．11．若数列{a n}的通项公式a n=5（）2n﹣2﹣4（）n﹣1（n∈N*），{a n}的最大项为第p项，最小项为第q项，则q﹣p等于（）A．1 B．2 C．3 D．4【考点】数列的函数特性．【分析】设=t∈（0，1]，a n=5（）2n﹣2﹣4（）n﹣1（n∈N*），可得a n=5t2﹣4t=﹣∈，利用二次函数的单调性即可得出．【解答】解：设=t∈（0，1]，a n=5（）2n﹣2﹣4（）n﹣1（n∈N*），∴a n=5t2﹣4t=﹣，∴a n∈，当且仅当n=1时，t=1，此时a n取得最大值；同理n=2时，a n取得最小值．∴q﹣p=2﹣1=1，故选：A．【点评】本题考查了二次函数的单调性、指数函数的单调性、数列的通项公式，考查了推理能力与计算能力，属于中档题．12．如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（，﹣），∠AOC=α，若|BC|=1，则cos2﹣sin cos﹣的值为（）A．B．C．﹣D．﹣【考点】任意角的三角函数的定义．【分析】由条件利用任意角的三角函数的定义求得cos（﹣α）、sin（﹣α）的值，可得cosα和sinα的值，从而求得所给式子的值．【解答】解：∵|BC |=1，点B 的坐标为（，﹣），故|OB |=1，∴△BOC 为等边三角形，∴∠BOC=，又∠AOC=α，∴∠AOB=﹣α，∴cos （﹣α）=，﹣sin （﹣α）=﹣，∴sin （﹣α）=．∴cos α=cos [﹣（﹣α）]=coscos （﹣α）+sinsin （﹣α）=+=，∴sin α=sin [﹣（﹣α）]=sincos （﹣α）﹣cos sin （﹣α）=﹣=．∴cos 2﹣sincos ﹣=（2cos 2﹣1）﹣sin α=cos α﹣sin α=﹣=，故选：A ．【点评】本题主要考查任意角的三角函数的定义，三角恒等变换，属于中档题．二、填空题（本大题共4小题，每题5分，共20分）13．在数列中，则实数a=，b=．【考点】数列的概念及简单表示法．【分析】由不完全归纳法知a ﹣b=26，a +b=15，从而解得． 【解答】解：由5，10，17，a ﹣b ，37知，a ﹣b=26，由3，8，a +b ，24，35知， a +b=15，解得，a=，b=；故答案为：，．【点评】本题考查了数列的性质的判断与归纳法的应用．14．已知tan β=，tan （α﹣β）=，其中α，β均为锐角，则α= ．【考点】两角和与差的正切函数．【分析】根据两角差的正切公式计算即可得解tan α=1，结合角α的范围即可得解．【解答】解：∵tan β=，α，β均为锐角，∴tan （α﹣β）===，解得：tan α=1，∴α=．故答案为：．【点评】本题考查了两角差的正切公式，掌握公式是关键，属于基础题．15．已知a ，b 是互异的负数，A 是a ，b 的等差中项，G 是a ，b 的等比中项，则A 与G 的大小关系为 A ＜G ．【考点】等比数列的通项公式；等差数列的通项公式．【分析】由等差中项和等比中项可得A 、G ，由基本不等式可得大小关系．【解答】解：由题意可得A=，G=±，由基本不等式可得A ≥G ，当且仅当a=b 取等号，由题意a ，b 是互异的负数，故A ＜G ．故答案是：A ＜G ．【点评】本题考查等差中项和等比中项，涉及基本不等式的应用，属基础题．16．已知数列{a n }中，2a n ，a n +1是方程x 2﹣3x +b n =0的两根，a 1=2，则b 5= ﹣1054 ．【考点】数列递推式．【分析】2a n ，a n +1是方程x 2﹣3x +b n =0的两根，利用根与系数的关系可得：2a n +a n +1=3，2a n a n +1=b n ，由a 1=2，可得a 2=﹣1，同理可得a 3=5，a 4=﹣7，a 5=17，a 6=﹣31．即可得出．【解答】解：∵2a n ，a n +1是方程x 2﹣3x +b n =0的两根，∴2a n +a n +1=3，2a n a n +1=b n ，∵a 1=2，∴a 2=﹣1，同理可得a 3=5，a 4=﹣7，a 5=17，a 6=﹣31． 则b 5=2×17×（﹣31）=1054．故答案为：﹣1054．【点评】本题考查了一元二次方程的根与系数的关系、递推关系，考查了推理能力与计算能力，属于中档题．三、解答题（本大题共6小题，共70分）17．已知cos （+θ）=﹣，＜θ＜，求的值．【考点】三角函数的化简求值．【分析】求出sin （+θ），从而sin θ+cos θ的值，由cos （+θ），得cos θ﹣sin θ的值，由此得到正弦函数与余弦函数点值，进而能求出的值．【解答】解：∵＜θ＜，∴ +θ∈（，），∵cos （+θ）=﹣，∴sin （+θ）=﹣=﹣，∴sin （+θ）=sin θcos+cos θsin=（cos θ+sin θ）=﹣，∴sin θ+cos θ=﹣，①cos （+θ）=coscos θ﹣sinsin θ=（cos θ﹣cos β）=﹣，∴cosθ﹣sinθ=﹣，②联立①②，得cosθ=﹣，sinθ=﹣，∴====．【点评】本题考查函数值的求法，是中档题，解题时要认真审题，注意三角函数诱导公式、加法定理和同角三角函数关系式的合理运用．18．已知△ABC的三边是连续的三个正整数，且最大角是最小角的2倍，求△ABC的面积．【考点】正弦定理．【分析】由题意设a=n、b=n+1、c=n+2（n∈N），由边角关系可得C=2A，由正弦定理和余+弦定理列出方程，求出n、三边、cosA的值，由平方关系求出sinA，代入三角形面积公式即可求出△ABC的面积．【解答】解：由题意设a=n、b=n+1、c=n+2（n∈N），+∵最大角是最小角的2倍，∴C=2A，由正弦定理得，则，∴，得cosA=，由余弦定理得，cosA==，∴=，化简得，n=4，∴a=4、b=5、c=6，cosA=，又0＜A＜π，∴sinA==，∴△ABC 的面积S===．【点评】本题考查正弦定理和余弦定理，边角关系，三角形的面积公式的综合应用，以及方程思想，考查化简、计算能力，属于中档题．19．已知数列{a n }的前n 项和S n =2n 2﹣19n +1，记T n =|a 1|+|a 2|+…+|a n |．（1）求S n 的最小值及相应n 的值；（2）求T n ．【考点】数列的求和；数列递推式．【分析】（1）S n =2n 2﹣19n +1=2﹣，利用二次函数的单调性即可得出．（2）由S n =2n 2﹣19n +1，n=1时，a 1=﹣16．n ≥2时，a n =S n ﹣S n ﹣1=4n ﹣21．由a n ≤0，解得n ≤5．n ≥6时，a n ＞0．可得n ≤5时，T n =|a 1|+|a 2|+…+|a n |=﹣（a 1+a 2+…+a n ）=﹣S n ．n ≥6时，T n =﹣（a 1+a 2+…+a 5）+a 6+…+a n =﹣2S 5+S n ．【解答】解：（1）S n =2n 2﹣19n +1=2﹣，∴n=5时，S n 取得最小值=﹣44． （2）由S n =2n 2﹣19n +1， ∴n=1时，a 1=2﹣19+1=﹣16．n ≥2时，a n =S n ﹣S n ﹣1=2n 2﹣19n +1﹣[2（n ﹣1）2﹣19（n ﹣1）+1]=4n ﹣21．由a n ≤0，解得n ≤5．n ≥6时，a n ＞0．∴n ≤5时，T n =|a 1|+|a 2|+…+|a n |=﹣（a 1+a 2+…+a n ）=﹣S n =﹣2n 2+19n ﹣1．n ≥6时，T n =﹣（a 1+a 2+…+a 5）+a 6+…+a n=﹣2S 5+S n =2n 2﹣19n +89．∴T n =．【点评】本题考查了等差数列的通项公式及其前n 项和公式、不等式的解法、绝对值数列求和问题，考查了分类讨论方法推理能力与计算能力，属于中档题．20．已知等差数列{a n }，等比数列{b n }满足：a 1=b 1=1，a 2=b 2，2a 3﹣b 3=1．（Ⅰ）求数列{a n}，{b n}的通项公式；（Ⅱ）记c n=a n b n，求数列{c n}的前n项和S n．【考点】数列的求和；等差数列的通项公式；等比数列的通项公式．【分析】（I）设等差数列{a n}的公差为d，等比数列{b n}的公比为q，由a1=b1=1，a2=b2，2a3﹣b3=1．可得1+d=q，2（1+2d）﹣q2=1，解出即可得出．（II）当时，c n=a n b n=1，S n=n．当时，c n=a n b n=（2n﹣1）3n﹣1，利用“错位相减法”与等比数列的前n项和公式即可得出．【解答】解：（I）设等差数列{a n}的公差为d，等比数列{b n}的公比为q：∵a1=b1=1，a2=b2，2a3﹣b3=1．∴1+d=q，2（1+2d）﹣q2=1，解得或．∴a n=1，b n=1；或a n=1+2（n﹣1）=2n﹣1，b n=3n﹣1．（II）当时，c n=a n b n=1，S n=n．当时，c n=a n b n=（2n﹣1）3n﹣1，∴S n=1+3×3+5×32+…+（2n﹣1）3n﹣1，3S n=3+3×32+…+（2n﹣3）3n﹣1+（2n﹣1）3n，∴﹣2S n=1+2（3+32+…+3n﹣1）﹣（2n﹣1）3n=﹣1﹣（2n﹣1）3n=（2﹣2n）3n ﹣2，∴S n=（n﹣1）3n+1．【点评】本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”，考查了推理能力与计算能力，属于中档题．21．已知向量=（，1），=（cos，），记f（x）=．（1）求函数f（x）的最小正周期和单调递增区间；（2）将函数y=f（x）的图象向右平移个单位得到y=g（x）的图象，讨论函数y=g（x）﹣k在的零点个数．【考点】三角函数中的恒等变换应用；平面向量数量积的运算；正弦函数的图象．【分析】（1）通过平面向量数量积的运算，三角函数的恒等变形得到f（x）=sin（+）+，根据正弦函数的性质求函数f（x）的最小正周期和单调递增区间；（2）先求得y=g（x）﹣k的解析式，从而可求g（x）的值域，由函数y=g（x）的图象与直线y=k在的上有交点，可得实数k的取值范围．【解答】解：（1）∵向量=（，1），=（cos，），记f（x）=．∴f（x）=cos+=sin+cos+=sin（+）+，∴最小正周期T==4π，2kπ﹣≤+≤2kπ+，则4kπ﹣≤x≤4kπ+，k∈Z．故函数f（x）的单调递增区间是[4kπ﹣，4kπ+]，k∈Z；（2））∵将函数y=f（x）=sin（+）+的图象向右平移个单位得到函数解析式为：y=g（x）=sin[（x﹣+）]+=sin（﹣）+，∴则y=g（x）﹣k=sin（x﹣）+﹣k，∵x∈[0，]，可得：﹣≤x﹣≤π，∴﹣≤sin（x﹣）≤1，∴0≤sin（x﹣）+≤，∴若函数y=g（x）﹣k在[0，]上有零点，则函数y=g（x）的图象与直线y=k在[0，]上有交点，∴实数k的取值范围是[0，]．∴当k＜0或k＞时，函数y=g（x）﹣k在的零点个数是0；当0≤k＜1时，函数y=g（x）﹣k在的零点个数是2；当k=0或k=时，函数y=g（x）﹣k在的零点个数是1．【点评】本题是中档题，考查向量的数量积的应用，三角函数的化简求值，函数的单调增区间的求法，函数零点的判断方法，考查计算能力．22．已知点（1，）是函数f（x）=a x（a＞0且a≠1）的图象上一点，等比数列{a n}的前n=+项和为f（n）﹣c，数列{b n}（b n＞0）的首项为c，且前n项和S n满足S n﹣S n﹣1（n≥2）．记数列{}前n项和为T n，（1）求数列{a n}和{b n}的通项公式；（2）若对任意正整数n，当m∈[﹣1，1]时，不等式t2﹣2mt+＞T n恒成立，求实数t的取值范围（3）是否存在正整数m，n，且1＜m＜n，使得T1，T m，T n成等比数列？若存在，求出m，n的值，若不存在，说明理由．【考点】数列与函数的综合；等差数列的通项公式；等比数列的通项公式；等比关系的确定．【分析】（1）因为点是函数f（x）=a x的图象上一点，所以a=，所以f（x）=，即可得到数列的前3项，进而求出数列的首项与公比，即可得到数列{a n}的通项公式；因为=，所以数列{}是求出答案．以1为首项，以1为公差的等差数列，所以得到S n，利用b n=S n﹣S n﹣1（2）利用裂项相消的方法可得：T n=；进而把原不等式化简为：当m∈[﹣1，1]时，不等式t2﹣2mt＞0恒成立；设g（m）=﹣2tm+t2，m∈[﹣1，1]，然后利用函数的有界性解决恒成立问题即可得到答案．（3）利用T1，T m，T n成等比数列，得T m2=T1T n得到，，最后结合1＜m＜n知，m=2，n=12即可．【解答】解：（1）因为f（1）=a=，所以f（x）=，所以，a2=[f（2）﹣c]﹣[f（1）﹣c]=，a3=[f（3）﹣c]﹣[f（2）﹣c]=因为数列{a n}是等比数列，所以，所以c=1．又公比q=，所以；由题意可得：=，又因为b n＞0，所以；所以数列{}是以1为首项，以1为公差的等差数列，并且有；=2n﹣1；当n≥2时，b n=S n﹣S n﹣1所以b n=2n﹣1．（2）因为数列前n项和为T n，所以==；因为当m∈[﹣1，1]时，不等式恒成立，所以只要当m∈[﹣1，1]时，不等式t2﹣2mt＞0恒成立即可，设g（m）=﹣2tm+t2，m∈[﹣1，1]，所以只要一次函数g（m）＞0在m∈[﹣1，1]上恒成立即可，所以，解得t＜﹣2或t＞2，所以实数t的取值范围为（﹣∞，﹣2）∪（2，+∞）．（3）T1，T m，T n成等比数列，得T m2=T1T n∴，∴结合1＜m＜n知，m=2，n=12【点评】本题综合考查数列、不等式与函数的有关知识，解决此类问题的关键是熟练掌握数列求通项公式与求和的方法，以及把不等式恒成立问题转化为函数求最值问题，然后利用函数的有关知识解决问题．。

安徽省六安市第一中学2015-2016学年高一下学期周末作业（九）数学试题一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.化简：+-+-等于（ ）A ．B ．C ．D ．【答案】A【解析】 试题分析：+-+-=)(+-++=-+=AD ,故选A. 考点：向量的基本运算.2.已知平面向量),2(),2,1(m -==，且//，则=+32（ ）A ．)10,5(--B ．)8,4(--C ．)6,3(--D ．)4,2(--【答案】B3.设向量b a ,均为单位向量，且1||=+b a ，则a 与的夹角为（ ）A ．3πB ．2πC ．32πD ．43π 【答案】C【解析】 试题分析：由1||2=+得21-=⋅，解得21,cos ->=<，即夹角为32π,故选C. 考点：1、向量的基本运算；2、向量的数量积.4.在ABC ∆中，c AB =，b AC =，若点D 满足DC BD 2=，则=AD （ ）A - D + 【答案】A【解析】试题分析：=AD +=+=)(32AB AC AB -++ 考点：向量的基本运算．5.下列命题正确的是（ ）A ．若⋅=⋅，则=或=B ．若||||||⋅=⋅，则//C ．)1,1(-=a 在)4,3(=b 方向上的投影为51 D ．若向量a 与同向，且||||b a >，则b a > 【答案】B【解析】试题分析： ||||||⋅=⋅,∴||||⋅|,cos |><⋅||||⋅=,∴1|,cos |=><,∴//.故选B ． 考点：1、向量的数量积运算；2、共线向量；3、向量的投影.【易错点晴】本题主要考查向量的数量积运算、共线向量、向量的投影，虽然难度不大，但属于易错题.选项A 易误以为可以约分，选项C 易方向判断错误而代错公式，选项D 易误以为向量可以比较大小.向量知识概念比较多，也比较零碎,是根鸡肋，需要花时间去死抠定义和公式，并熟练掌握，才能处变不惊，从容应对.6.已知向量b a CD b a BC b a AB 33,35,3+-=+=+=，则（ ）A ．A ，B ，C 三点共线 B ．A ，B ，D 三点共线C ．A ，C ，D 三点共线 D ．B ，C ，D 三点共线【答案】B7.已知,为互相垂直的单位向量，2-=，λ+=，且，b 的夹角为锐角，则实数λ的 取值范围是（ ）A ．)21,(-∞B ．),21(+∞C ． ),32()32,2(+∞-D ．)21,2()2,(---∞【答案】D【解析】试题分析： a ，的夹角为锐角，∴0)2(21>-+⨯=⋅λb a 且01)2(1≠⨯--⨯λ，∴∈λ )21,2()2,(---∞ ，故选D. 考点：1、向量的夹角；2、向量的共线.8.在ABC ∆中，2||)(=⋅+，则ABC ∆的形状一定是（ ）A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形【答案】A【解析】 试题分析：由2||)(=⋅+得0)(=⋅-+AC AC BA BC ,即0)(=⋅++AC CA BA BC ,∴ 02=⋅AC BA ，∴AC BA ⊥，∴ABC ∆为直角三角形，故选A.考点：1、向量的加法法则；2、向量的数量积.9.ABC ∆是边长为2的等边三角形，已知向量，满足+==2,2，则下列结论正 确的是（ ）A ．1||=B ．⊥C ．1=⋅D ．⊥+)4(【答案】D10.在直角ABC ∆中，CD 是斜边AB 上的高，则下列等式不成立的是（ ）A ．AB AC AC ⋅=2|| B ．BC BA BC ⋅=2||C ．⋅=2||D ．22||))||AB BC BA AB AC =【答案】C【解析】试题分析：法一：由直角三角形可得0=⋅BC AC 得，0)(=-⋅AB AC AC ，∴⋅=2||成立， 同理BC BA BC ⋅=2||也成立，D 选项等价于||||||2BD AD CD ⋅=，该命题显然成立，故选C.法二：直接观察选项C 中的0<⋅CD AC ，因此等式显然不成立，故选C.考点：1、向量的加法法则；2、向量的数量积；3、投影；4、直角三角形的射影定理.【思路点晴】本题主要考查向量的加法法则、向量的数量积、向量的投影、直角三角形的射影定理，属于中档题.要做好本题需要熟练掌握向量的加法法则和向量的投影定义，并能及时联想到直角三角形的射影定理，才能及时突破难点.当然，思维敏捷的 同学可以直接观察选项C 中的右端是负数，显然不成立，可以规避难点，直捣黄龙！11.如图，已知圆M ：4)3()3(22=-+-y x ，四边形ABCD 为圆M 的内接正方形，F E ,分别 为边AD AB ,的中点，当正方形ABCD 绕圆心M 转动时，⋅的最大值是（ ）A ．2B ．3C ．4D ．6【答案】D【思路点晴】本题主要考查向量的基本运算、向量的数量积和余弦函数的值域，本题综合性较强，属于难题. 经过多次向量运算变形后将OF ME ⋅转化为OM FA ⋅，再利用数量积公式和余弦函数的值域，即可顺利求出OF ME ⋅的最大值，其中将OF ⋅转化为OM FA ⋅是本题最难之处，也是本题的亮点,平时应该加强这方面的训练.12.如图，四边形ABCD 是正方形，延长CD 至E ，使得CD DE =.若动点P 从点A 出发，沿正 方形的边按逆时针方向运动一周回到A 点，其中μλ+=，下列判断正确．．的是（ ） A ．满足2=+μλ的点P 必为BC 的中点B ．满足1=+μλ的点P 有且只有一个C ．满足μλ+的最大值为3D ．满足μλ+的最小值不存在【答案】C考点：1、向量的几何运算；2、向量的坐标运算；3、向量的数乘.【方法点晴】本题主要考查向量的集合运算、向量的坐标运算和向量的数乘，既考查了数学结合思想，又考查了分类讨论思想.属于难题.要求学生熟练掌握向量的相关知识，懂得将图形坐标化（解析化），灵活选用向量的几何法和代数法，并对P 点位置(即P AB ∈ ，∈P BC ，P CD ∈ 三种情况）进行分类讨论,合理排除错误选项.第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每题5分，满分20分．）13.若5||,8||==，则||的取值范围是 .【答案】]13,3[【解析】 试题分析：根据||||||-||±≤≤||||+易得||的取值范围是]13,3[.考点：1、向量的模；2、向量的几何运算.14.在ABC Rt ∆中， 90=∠A ，2==AC AB ，点D 为AC 中点，点E 满足BE =，则 =⋅ .【答案】2-15.如图，在ABC ∆中，=P 是BN 上一点，若m +=，则实数m 的 值为 .【答案】113【方法点晴】本题主要考查向量的几何运算、平面向量的基本定理,属于中档题.解本题关键要巧妙运用三角形加法法则和向量的数乘，将AN 分解成811mAB AN + ，再利用性质：在ABN ∆中,如果：m AB = nAN + 则：1m n +=进行求解.这种题型如果通过集合运算求不出正确答案，亦可以选择建立直角坐标系，用解析法求解.16.设单位向量21,e e 对于任意实数λ都有|||211e e e λ-≤+，则向量21,e e 的夹角为 . 【答案】32π 【解析】试题分析：记t e e =⋅21，则将不等式||||211e e e λ-≤+左右两边平方原命题转化为：04122≥---t t λλ恒成立，即01442≤++=∆t t 恒成立，即t =21e e ⋅21-=，向量21,e e 的夹角为32π 考点：1、向量的模；2、向量的数量积；3、向量的夹角；4、二次函数的性质.【方法点晴】本题主要考查向量的模、向量的数量积、向量的夹角和二次函数的性质，综合性较强，属于较难题型.本题关键突破口是将不等式平方转化为：二次不等式恒成立问题，再利用判别式0≤∆进行求解求出21e e ⋅的值，进而求出夹角.用换元思想解题是本题最为灵巧之处，将本题化腐朽为神奇，化难为易，平时应注重这方面的积累.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.平面内有三个点)0,2(A ，)2,0(B ，)sin ,(cos ααC （其中),0(πα∈），点O 为坐标原点，且7||=+.（1）求α的值；（2）求向量与AC 的夹角.【答案】（1）3πα=；（2）65π.18.如图所示，)1,6(=，),(y x =，)3,2(--=，其中0>x .（1）若AD BC //，试求x 与y 之间的表达式；（2）在（1）的条件下，若又有⊥，试求x 、y 的值及四边形ABCD 的面积.【答案】（1）02=+y x ；（2）⎩⎨⎧-==12y x 或⎩⎨⎧=-=36y x ，16．19.如图，O 是ABC ∆所在平面内一点， 150=∠AOB150=∠AOB ，向量OC OB OA ,,的模分 别为4,3,2.（1）求||++；（2）若OB n OA m OC +=，求实数n m ,的值.【答案】（1）3||=++；（2）4-==n m .【解析】试题分析：（1）将||OC OB OA ++平方，再利用向量基本运算进行解题；（2）化简OB n OA m OC +=即可得方程组，再解相关方程组.试题解析：(1) 150=∠AOB 150=∠AOB ∴90=∠BOC ∴30-=⋅B OA ,00=⋅B OC ,40-=⋅C OA ∴2||OC OB OA ++2()OA OB OC =++2OA = 2OB + 2OC + 20OA B +⋅ 20OC B +⋅ 209OA C +⋅= ,∴3||=++（2）由OB n OA m OC +=可得，所以⎩⎨⎧=+--=-033434n m n m ，解得4-==n m考点：1、向量的模；2、向量的数量积；3、向量的相等.20.已知O 是ABC ∆所在平面内一点.（1）已知D 为BC 边中点，且2=++，证明：=；（2）已知32=++，BOC ∆的面积为2，求ABC ∆的面积.【答案】（1）证明见解析；（2）12.（2）如图所示，延长OB 到'B ，使OB OB 2'=，延长OC 到'C ，使OC OC 3'=，连结''C B ，取''C B 的中点'A ，则-==+232，所以A ，O ，'A 三点共线且O 为三角形''C AB 的重心，则''''OC B AOC AOB S S S ∆∆∆==，在'AOB ∆中，B 为'OB 边中点，所以'21AOB AOB S S ∆∆=，在'AOC ∆中，C 为'OC 边近O 端三等分点，所以'31AOC AOC S S ∆∆=，在''OC B ∆中，连'BC ，B 为'OB 边中点，所以''21OC B BOC S S ∆∆=，在'BOC ∆中，C 为'OC 边近O 端三等分点，所以'''6131OC B BOC BOC S S S ∆∆∆==，所以AOB ∆，AOC ∆，BOC ∆面积之比为21：31：361=：2：1，因为BOC ∆的面积为2，所以ABC ∆的面积为12)123(2=++⨯.考点：1、向量的几何运算；2、向量的数乘；3、三角形面积相似比.【方法点晴】本题主要考查向量的几何运算、向量的数乘和三角形面积相似比，属于难题.要解决本题关键要懂得将2、3几何化并作出三角形''C AB ，证明O 为三角形''C AB 的重心，再利用线段的比例关系，求得AOB ∆，AOC ∆，BOC ∆面积之比为21：31：361=：2：1，这是另一个关键难点. 21.如图，在平面斜坐标系xOy 中， 60=∠xOy ，平面上任一点P 的斜坐标定义如下：若21e y e x OP +=（其中21,e e 分别为与x 轴，y 轴同方向的单位向量），则点P 的斜坐标为(),x y .此时有 )2,1(=OA ，)4,(a OB =，试在该斜坐标系下探究以下问题：（1）OB OA //，求的坐标；（2）)4,3(=，求⋅的值；（3）求与同向的单位向量的坐标.【答案】（1）)4,2(=OB ；（2）16=⋅OB OA ；（3）)772,77(. B ’C ’【方法点晴】本题主要考查平面向量的基本定理、向量的平行、向量的数量积和单位向量，属于难题.本题的主要难点是要通过非正交坐标系与正交坐标系进行类比，将正交坐标系中向量的平行、向量的数量积和单位向量对应的知识迁移到非正交坐标系中进行求解.这就要求考生既要熟练掌握向量的相关知识，还考查了考生的合情推理能力.。