5816高一年级数学上学期期末模拟试题一

2020学年第一学期期末模拟考高一年级数学学科试题考试须知：1．本卷共4页满分150分，考试时间120分钟．2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号即准考证号并填涂相应数字． 3．所有答案必须写在答题纸上，写在试卷上无效． 4．考试结束后，只需上交答题纸．选择题部分一、单行选择题（每题5分，共40分）1．已知集合{}20A x x =->∣，{}1,0,1,3,4B =-，则()=U C A B ⋂（ ） A ．∅B ．{}1C ．{}1,0,1-D ．{}0,1,22．命题“任意实数2,0x x ≥”的否定是（ ）A ．任意实数2,0x x <B ．存在实数2,0x x <C ．任意实数2,0x x ≤D ．存在实数2,0x x ≤3．设x R ∈，则“15x -<<”是“5x <”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．函数()3ln f x x x=-的零点所在的大致区间是（ ） A ．()1,2B ．()2,3C ．()3,4D ．()3,+∞5．角α的终边经过点()2,1-，则2sin 3cos αα+的值为（ ）A ．5B 5C 45D ．456．若1a >，同一坐标系，函数xy a -=与 log a y x =-的图像可能是（ ）A ．B ．C ．D ．7．已知0.20.5a =，0.6log 2b =，0.6log 0.2c =，则a 、b 、c 的大小关系为（ ） A ．a c b <<B ．a b c <<C ．b a c <<D ．b c a <<8．已知函数()2cos 23f x x π⎛⎫=-⎪⎝⎭，则下列说法正确的是（ ） A ．()f x 的最小正周期为2πB ．()f x 的图象关于直线56x π=C ．()f x 的一个零点为6π D ．()f x 在区间,63ππ⎡⎤⎢⎥⎣⎦的最小值为1 二、多项选择题（每题5分，共20分）9．下列函数中，选出在定义域内单调递增的是（ ）A ．11y x -=-B ．3122xy ⎛⎫=- ⎪⎝⎭C ．()es log 43y x =-D ．lgx 10y =10．对任意两个实数a 、b ，定义{},min , ,a a ba b b a b≤⎧=⎨>⎩，若()23f x x =-，()21g x x =-．下列关于函数()()(){}min ,F x f x g x =的说法正确的是（ ） A ．函数()F x 是偶函数；B ．方程()0F x =有两个解；C ．方程()F x m =可能有三个根；D ．函数()F x 有最大值1，无最小值．11．下列关于基本不等式的说法正确的是（ ）A ．若103x <<，则() 13x x -的最大值为112B ．函数()23311x x y x x ++=>-+的最小值为2C ．已知1x y +=，0x >，0y >，则121x x y ++的最小值为54D ．若整数x ，y 满足220x xy +-=，则3x y +的最小值是312．已知函数()(),af x x a R x=+∈，方程() 4f x =在[)0,+∞有两个解12,x x ，记()12g a x x =-，则下列说法正确的是（ ） A ．函数()f x 的值域是[)0,+∞ B ．若1a =-，()f x 的增区间为[)1,0-何[)1,+∞ C ．若4a =，则()0g a =D ．函数()g a 的最大值为4非选择题部分三、填空题（每题5分，共30分）13．幂函数()f x 的图象经过点()4,2，则12f ⎛⎫=⎪⎝⎭_____________． 14．若1sin 33πα⎛⎫-=-⎪⎝⎭，则cos 6πα⎛⎫+= ⎪⎝⎭___________．15．一个扇形周长为8，则扇形面积最大时，圆心角的弧度数是__________．16．已知函数()lg ,01,0x x f x x x ⎧>=⎨+≤⎩∣，若函数()y f x a =-有3个零点，则实数a 的取值范围是_______．17．已知函数()()af x x a R x=+∈满足下列四个条件中的三个：①函数()f x 是奇函数；②函数()f x 在区间(),5-∞-上单调递增；③()()22f f <-；④在y 轴右侧函数()f x 的图象位于直线y x =上方，写出一个符合要求的函数________________________．18．当一个非空数集G 满足“如果,a b G ∈，则a b +，a b -，ab G ∈，且0b ≠时，aG b∈”时，我们称G 就是一个数域，以下关于数域的命题：①0和1都是任何数域的元素；②若数域G 有非零元素，则2020G ∈；③任何一个有限数域的元素个数必为奇数；④有理数集是一个数域；⑤偶数集是一个数域，其中正确的命题有______________． 四、解答题（每题12分，共60分） 19．（本小题满分12分） 设不等式402xx ->-的解集为集合A ，关于x 的不等式()()120x m x m +-+-<的解集为集合B ． （1）若2m =-，求R A C B ⋂；（2）命题p :x A ∈,命题q :x B ∈,若p 是q 的必要不充分条件，求实数m 的取值范围． 20．（本小题满分12分）已知函数()232cos 2x f x x m =++在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值为6， （1）求常数m 的值；（2）若()145f α=，且433ππα<<，求 6f πα⎛⎫- ⎪⎝⎭的值． 21．（本小题满分12分）已知函数()()2log 3x f x x ax =-+-，其中()0,1a a >≠． （1）当4a =时，求()f x 的值域和单调区间； （2）若()f x 存在单调递增区间，求a 的取值范围． 22．（本小题满分12）在2020年初，新冠肺炎疫情袭击全国，丽水市某村施行“封村”行动．为了更好地服务于村民，村卫生室需建造一间地面面积为30平方米且墙高为3米的长方体供给监测站．供给监测站的背面靠墙，无需建造费用，因此甲工程队给出的报价为：正面新建墙体的报价为每平方米600元，左右两面新建墙体报价为每平方米360元，屋顶和地面以及其他报价共计21600元，设屋子的左右两侧墙的长度均为x 米()310x ≤≤．（1）当左右两面墙的长度为多少时，甲工程队报价最低，最低报价为多少？（2）现有乙工程队也参与此监测站建造竞标，其给出的整体报价为()()216020a x a x+=>元，若无论左右两面墙的长度为多少米，乙工程队都能竞标成功，试求a 的取值范围．23．（本小题满分12分）已知函数()f x 定义域为D ，若同事满足一下条件：①()f x 在D 上单调递增或单调递减；②存在区间[],a b D ⊆，使()f x 在[],a b 上的值域是[],a b ，那么称()()f x x D ∈是闭函数．（1）求闭函数()3f x x =-符合件②的区间[],a b ；（2）判断函数()2lg f x x x =+是否为闭函数，若是请找出区间[],a b ；若不是，请说明理由； （3）若()2f x k x =+k 的取值范围．。

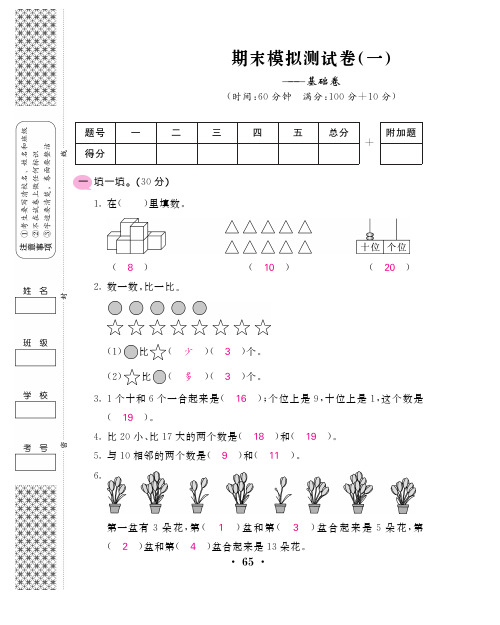
基础卷(时间:６０分钟㊀满分:１００分＋１０分)题号一二三四五总分＋附加题得分一填一填.(３０分)１ 在(㊀㊀)里填数.(　８　)㊀㊀㊀㊀㊀㊀㊀㊀㊀(　１０　)㊀㊀㊀㊀㊀㊀㊀(　２０　)２ 数一数,比一比.(１)比(　少　)(　(２)比(　多　)(　３３ １个十和６个一合起来是(　１６　);个位上是９,十位上是１,这个数是(　１９　).４ 比２０小㊁比１７大的两个数是(　１８　)和(　１９　).５ 与１０相邻的两个数是(　９　)和(　１１　).６第一盆有３朵花,第(　１　)盆和第(　３　)盆合起来是５朵花,第(　２　)盆和第(　４　)盆合起来是１３朵花.５６７ 小朋友们排成一队做游戏.小东左边有７个人,右边有５个人这一队共有(　１３　)个人.８ 用相同的小正方体拼一个大正方体至少要用(　８　)个小正方体.９１０ １０比７大(　３　),比１３多４的数是(　１７　).１１ 认识钟表.㊀㊀　１１　时㊀㊀㊀㊀㊀㊀　６　:　００　㊀㊀㊀㊀㊀快　３　时了二按要求做一做.(共１２分)１(１)正方体有(　２　)个,长方体有(　４　)个,球有(　３　)个,圆柱体有(　２　)个.(４分)(２)从左边数,第３个图形和第１０个图形之间有(　６　)个图形.(２分)(３)把右边的４个图形圈起来.(１分)２ 看一看,填一填.(３分)(１)在的左面画.(２)在的上面画.(３)在的右面画.３ 找出规律后接着往下涂色.(２分)６６三算一算.(共３０分)１ 口算.(１２分)３＋５＝８㊀㊀㊀７＋４＝１１㊀㊀㊀１５－２＝１３㊀㊀㊀１３＋２－５＝１０８＋７＝１５１０－１＝９６＋６＝１２６＋８－３＝１１５＋０＝５９－３＝６５＋９＝１４１６－１０＋７＝１３２ 在里填上 ＞ ㊁ ＜ 或 ＝ .(６分)５＋７＜１３㊀㊀㊀㊀㊀㊀７＞１６－１０㊀㊀㊀㊀㊀㊀７＋８＜１７１０－７＜６１４＞４＋９８＋６＝１４３ 在㊀里填数.(１２分)１６－６＝１０８＋５＝１３１０－３＝７１５－１０＝５３＋８＝１０＋１１３－９＝４四看图列式.(１２分)１ ㊀㊀２㊀㊀７＋４＝１１(只)㊀㊀１３－３＝１０(个)３ ４㊀㊀６＋３＋４＝１３(朵)㊀１５－３－２＝１０(个)７６五解决问题.(共１６分)１ 一共钓了几条鱼?(４分)７＋１２＝１９(条)２ (４分)１０－４＝６(个)３ １６个小朋友,每人吃一个蛋糕,还需要多少个蛋糕?(４分)４ 他们一共采了多少个松果?(４分)８＋８＝１６(个)智力冲浪(附加题)㊀㊀把２,３,４,５,６这５个数填在里,使横行㊁竖行上的三个数相加的结果都等于１２.(１０分)８６。

小学一年级数学上册期末模拟试卷及答案(三篇)目录：小学一年级数学上册期末模拟试卷及答案一小学一年级数学上册期末模拟题及答案二小学一年级数学上册期末水平测试卷及答案三小学一年级数学上册期末模拟试卷及答案一班级：姓名：满分：100分考试时间：90分钟一、我会算。

（20分）87-16＝23＋47＝60－20＝63+14＝15＋32＝97－50＝23+32＝54-13＝13+15＝79-19＝7+51＝46-38＝30+60＝88-15＝62+16＝85-34＝二、填空题。

（20分）1、8前一个数是________，后一个数是________。

2、与18相邻的数是________和________。

3、折出了（____）个相同的（____）形。

4、在16这个数中，个位上的数是_____ ，表示___个 _____ ；十位上的数是_____，表示__ 个_____。

5、最大的两位数是（____），最小的三位数是（____），它们相差（____）。

6、1角=________分1元=________角9角=________分28角=________元________角7、8元6角93角15元15角3元5角（_____）＞（_____）＞（_____）＞（_____）＞（_____）8、（____）个（____）个（____）个（____）个9、20前面的数是（________），15后面的数是（________）。

10、4个一和2个十合起来是（_____）。

100里面有（_____）个十。

三、选择题。

（10分）1、同学们站队，小红前面有12人，后面有7人，这排队伍一共有（）人。

A．19 B．20 C．212、2.35元中的“3”表示的意思是（）.A．3元B．3角C．3分3、钟面上的时针指向6时，那么分针指向（）。

A．3 B．6 C．124、下面哪个数与47最接近？（）。

A．41 B．74 C．515、一辆公共汽车上有28人，到站后下车8人，上车10人。

新部编人教版一年级数学上册期末模拟试卷及答案(三篇)目录：新部编人教版一年级数学上册期末模拟试卷及答案一新部编人教版一年级数学上册期末模拟题及答案二新部编人教版一年级数学上册期末水平测试卷及答案三新部编人教版一年级数学上册期末模拟试卷及答案一班级：姓名：满分：100分考试时间：90分钟题序一二三四五总分得分一、我会算。

（20分）6+10= 16-4= 6+12= 18-3=3+7= 9+5= 9-6= 7-5=11+7= 12+3= 19-7= 13-10=4+6 = 7+8= 9-4= 17-7=3+5-4= 4+0+6= 9-2+3= 18-8+2=二、填空题。

（20分）1、声音每秒在空气中行332米，炮弹每秒比声音快667米，炮弹每秒飞行（_____）米。

2、一个两位数,十位上的数是 6,个位上的数是 9,这个数是（______）,和这个数相邻的两个数分别是（______）和（______）。

3、一个数的个位上是2，十位上是1，这个数是（______），它在（______）的后面。

4、最大的—位数是（______），最小的两位数是（______），它们的和是（______）。

5、比一比（在横线上填上“＞”“＜”或“＝”）5+9________14 9________18-10 7+8________16 10-8________76、我会从大到小排一排。

（_____）>（______）>（______）>（______）>（______）7、在里填上“>”“<”或“＝”。

4 35 2 0 1 3＋1 45 5 3 1 2 4 5－1 38、11的前一个数是（______），后一个数是（______）。

9、（_______）时整，时针和分针成一条直线。

（_______）时整，时针和分针完全重合。

10、与17相邻的两个数是________和________。

教学资料参考范本部编版精选水平一年级上学期小学数学期末模拟试卷卷(四套)目录：部编版精选水平一年级上学期小学数学期末模拟试卷卷一部编版精选水平一年级上学期小学数学期末模拟试卷卷二部编版精选水平一年级上学期小学数学期末模拟试卷卷三部编版精选水平一年级上学期小学数学期末模拟试卷卷四部编版精选水平一年级上学期小学数学期末模拟试卷卷一 时间：60分钟 满分：100分一、基础练习(40分)1. 看图写数。

2. 和5＋3算式相等的式子是（ ）A .6＋3B .3＋5C .6－33. 13里面有______个十和______个一，由1个十和1个一组成的数题号 一 二 三 总分 得分是______。

4. 与10相邻的数是______和______。

5. 12的个位上是______，表示______个______。

6. 填一填。

______>10 15<____________+______=16 ______-______=1 67. 看图列算式。

1.（1）2.（2）3.（3）8. 看图填空1.（1）一共有______只动物，从左往右数，______排第3。

2.（2）从右往左数，______排第4，它前面有______只动物。

3.（3）把右边的三只动物圈起来，把左数第2只涂成黑色。

二、综合练习(40分)9. 大的画“√"，小的画“○”。

10. 圈一圈。

(把每行中不同类的圈出来)11. 算一算。

7-4=______ 8+8=______ 5+7=______ 10-3+9=______ 10+5=______ 12+6=______ 15-0=______ 9-8-1=______ 12. 在□填上适当的数。

13. 在14. 数一数，填一填。

15. 看图写算式。

三、应用练习(20分)16. 猜一猜。

小羊的年龄比小象大，比熊猫小，它可能几岁了？画“√”。

17. 圈一圈，把每题中不同类的圈出来18. 停车场原来有12辆车，开出去______辆，又开来______辆车，现在有多少辆车______ ?□○□○□=□19. 一共有多少个同学？20. 看图回答部编版精选水平一年级上学期小学数学期末模拟试卷卷二时间：60分钟满分：100分题号一二三总分得分一、基础练习(40分)1. 直接写得数。

2020年人教版一年级数学上册期末模拟试卷及答案(四套)目录：2020年人教版一年级数学上册期末模拟试卷及答案一2020年人教版一年级数学上册期末水平测试卷及答案二2020年人教版一年级数学上册期末水平测试题及答案三2020年人教版一年级数学上册期末测试及答案四2020年人教版一年级数学上册期末模拟试卷及答案一班级：姓名：满分：100分考试时间：90分钟一、我会算。

（20分）20＋6＋9＝60－20－30＝45＋40－10＝93－60＋8＝76－(25＋5)＝38＋(42＋8)＝82－30－7＝92－(54－50)＝24＋(49－9)＝二、填空题。

（20分）1、96里面有（____）个十和（____）个一，再加上（____）个一就是100。

2、一个长方体上面和前面的面积之和是209平方厘米，如果它的长、宽、高都是素数，那么它的面积是________平方厘米3、横线可以填几个数.6+________＜12 15-________＞8 17－_______＞8 9+_______＜164、最大的两位数是（_______），最小的两位数是（_______）。

5、6前面一个数是（________），后面一个数是（________）。

6、比一比（在横线上填上“＞”“＜”或“＝”）5+9________14 9________18-10 7+8________16 10-8________77、最小的自然数是（______）。

8、有块表（如图），当时针从下表所示时间走到4时整时，分针和时针重合了________次．9、比12多3的数是（________），比16少2的数是（________）。

10、一张100元可以换（______）张50元。

一张50元可以换（______）张10元。

三、选择题。

（10分）1、看图列式，算式正确的是( )。

A．3+5=8 B．3+7=10 C．3+4=72、求3个8的和，用（）法计算比较简便。

一年级上册数学期末测试卷一.选择题(共6题, 共12分)1.图中, 有（）个圆柱。

A.1B.2C.3D.42.我8时整睡觉, 妈妈比我晚睡1小时。

妈妈睡觉的时间是（）。

A.9时B.10时C.11时3.8＋2＋3与7＋3＋3结果（）。

A.不同B.相同C.无法比较4.学校开展运动会, 二（1）班有12人参加了跑步, 15人参加了游泳, 16人参加了跳绳。

参加（）的人最少。

A.游泳B.跑步C.跳绳5.选择合适的时间: （）。

A.早4时B.上午10时C.早7时6.数一数, 下图中表示数字（）。

A.10B.8C.6二.判断题(共6题, 共12分)1.羽毛球比篮球重。

（）2.姐姐在弟弟的左面, 弟弟在姐姐的右面。

( )3.在的下边。

（）4.4和9相比, 4离10远。

( )5.这个纸杯是圆柱。

（）6.○○○○○○○△△还需要画5个△就和○一样多。

（）三.填空题(共8题, 共17分)1.1个十, 5个一, 合起来是（）。

2.教室里, 讲桌在我的________面, 我用________手写字。

3.被减数是10, 减数是2, 差是（）。

4.一个数的十位上是1, 个位上是5, 这个数是（）。

5.数一数, 写数字。

（）（）6.填一填。

6+□=107+□=109+□=108+□=105+□=1010+□=107.19前面的一个数是_____, 后面的一个数是_____。

8.有( ) 个, 有( ) 个。

四.计算题(共3题, 共24分)1.口算。

11－3=_____ 18－9=_____ 15－6=_____15－5=_____ 7＋10=_____ 18－5=_____ 11－9=_____ 10－4=_____ 9＋9=_____ 16－7=_____ 11＋4=_____ 13－6=_____ 2.先说出得数再写算式。

3.在□里填上正确的数。

五.作图题(共2题, 共9分)1.看图照样子圈数。

2. 你能给下面的钟面画上分针吗?六.解答题(共6题, 共26分)1.车上原来有5人, 又上车2人, 到站下车4人。

高一年级数学上学期期末模拟试题（一）一．填空题：（本大题共14小题，每小题5分，共70分）1. 若幂函数的解析式为()(2)af x a x=-，则____.a=2 ________.3．若1cos,(2,2)2Aθθθππ⎧⎫==∈-⎨⎬⎩⎭，则集合A的子集有____个.4.已知函数()f x的图象是连续不断的，观察下表：x -2 -1 0 1 2()f x-6 3 -3 -2 1函数()f x在区间[-2,2]上的零点至少有_____个.5. 若b与(1,1)a=垂直，且2b=，则b的坐标为_______.6. 已知实数a，b均不为零，βααααtansincoscossin=-+baba，且6π=-αβ，则ab等于＝_____.7.已知函数13log()y x m=+的图象不经过第三象限，则实数m的取值范围是____________.8. 已知4cos,,0454x xππ⎛⎫⎛⎫+=∈-⎪ ⎪⎝⎭⎝⎭，则sin________.x=9. 设,A y yB x y⎧⎧⎪⎪====⎨⎨⎪⎪⎩⎩,则______.A B=10.若函数f(x)同时具有以下两个性质：①f(x)是偶函数；②对任意实数x，都有f(4xπ-)=f(4xπ+)，则下列函数中，符合上述条件的有_________.（填序号）①f(x)=cos4x②f(x)=sin(2x2π+) ③f(x)=sin(4x2π+)④f(x) = cos(32π-4x)11.已知向量2||||a bpa b=+，其中a、b均为非零向量，则||p的取值范围是_______.12.已知函数()sin(),()2cos()f x xg x xωϕωϕ=+=+若对任意的x R∈都有()()33f x f xππ+=-,则(3gπ=__________.13. 已知函数2()22(4)1f x mx m x=--+，(),g x mx=，若对于任一实数x，()f x与()g x至少有一个为正数，则实数m的取值范围是________.14.已知函数()|21|xf x=-，当a b c<<时，有()()()f a f c f b>>．给出以下结论：（1）0a c+<；（2）0b c+<；（3）222a c+>；（4）222b c+>．其中正确的结论序号为_________.二．解答题：15.如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角αβ，，它们的终边分别交单位圆于A B，两点．已知A B，．（1）求tan tanαβ和的值；（2）求αβ+的值．16.已知)cos2,sin(cos),sin,sin(cos xxxbxxxa-=+=,设xf=)((1)求函数)(xf的最小正周期，并写出)(xf的减区间；(2)当[0,2xπ∈时,求函数)(xf的最大值及最小值.17．商场销售某一品牌的羊毛衫，购买人数是羊毛衫标价的一次函数，标价越高，购买人数越少.把购买人数为零时的最低标价称为无效价格，已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件，商场以高于成本价的价格（标价）出售. 问：（1）商场要获取最大利润，羊毛衫的标价应定为每件多少元？（2）通常情况下，获取最大利润只是一种“理想结果”，如果商场要获得最大利润的75%，那么羊毛衫的标价为每件多少元？18.若函数1()(01)1xxaf x a aa-=>≠+且.⑴判断)(xf的奇偶性；⑵当1a>时，判断)(xf在(,)-∞+∞上的单调性，并加以证明.19. 已知坐标平面内O为坐标原点，(1,5),(7,1),(1,2),OA OB OM===P是线段OM上一个动点.当PA PB⋅取最小值时，求OP的坐标，并求cos APB∠的值.20．设函数f(x)=log a(x－3a)，g(x)=log aax-1，(a>0且a≠1).(1)若125a=，当11[2,3]2525x∈++时，求证：|f(x)－g(x)|<1；(2)当x∈［a+2,a+3］时，恒有|f(x)－g(x)|≤1,试确定a的取值范围.参考答案1．3 2.12 3.16 4.35. (或7.(,1]-∞8.9.(1,2]10.①③ 11.[1,3] 12.0 13.(0,8) 14.(1)(4)15.解：由题意，得A B ……2分 （1）tan 2,tan 3αβ==………………6分 （2）由（1）得t a n t a n 23t a n ()11t a n t a n 123αβαβαβ+++===---⨯……9分又(0,),(0,),22ππαβ∈∈则(0,)αβπ+∈……10分 34αβπ∴+=………………12分16．解：由题意，得()(cos sin )(cos sin )2sin cos f x a b x x x x x x =⋅=+-+＝cos 2sin 2x x +)4x π+…………4分（1）22T ππ==………………6分 3222,242k x k k Z πππππ+≤+≤+∈ 解得5,88k x k k Z ππππ+≤≤+∈()f x ∴的减区间为：5[,],88k k k Z ππππ++∈…………8分（直接写答案不扣分）（2）当[0,]2x π∈时，52[,]444x πππ+∈s i n (2)124x π∴-≤+≤，故max ()()8f x f π==，min ()()12f x f π==-……14分（不写对应x 的值不扣分，在必修4的教参上有考证）17．解：（1）(1)解：设购买人数为n 人，羊毛衫的标价为每件x 元，利润为y 元， 则(100,300]x ∈)0(<+=k b kx n ，∵b k +=3000，即k b 300-=，∴)300(-=x k n …………3分k x k x k x y 00010)200()300()100(2--=--= (x ∈(100，300])…………………6分∵k ＜0，∴x = 200时，y max =－10 000k ，即商场要获取最大利润，羊毛衫的标价应定为每件200元．……………………8分(2)解：由题意得，k (x －100)(x －300) =－10 000k ·75%0500374002=+-x x 解得x = 250或x = 150所以，商场要获取最大利润的75%，每件标价为250元或150元………………16分 18．（1）解：由()f x 的定义域为(,)-∞+∞，关于数0对称……………………2分11()()11x xx xa a f x f x a a-----===-++，得 ()f x ∴为R 上的奇函数.………………………………………………6分（2）当1a >时，)(x f 在(,)-∞+∞上的单调递增.……8分（本次未扣分，以后考试一定会扣分）证明：设12,x x 为(,)-∞+∞上任意两个实数，且12x x <，则由1a >得12x xa a <()()1212121212112()()()01111x x x x xx x x a a a a f x f x a a a a ----=-=<++++ ∴当1a >时，)(x f 在(,)-∞+∞上的单调递增.………………14分19．解：由题意，可设(,2)OP λλ=，其中[0,1]λ∈，则(1,52),(7,12)PA PB λλλλ=--=--………………………………4分 设()f PA PB λ=⋅，则2()(1)(7)(52)(12)52012f λλλλλλλ=--+--=-+，[0,1]λ∈…8分又()f λ在[0,1]上单调递减∴当1λ=时()f λ取得最小值，此时P 点坐标为(1,2)………………12分 (0,3),(6,1)PA PB ==-…………………………………………………14分cosPA PBAPBPA PB⋅∴∠===…………………………16分20．解：22()()log(3)()log(43)a af xg x x a x a x ax a-=--=-+令22()43h x x ax a=-+，则当01a<<时，()h x的对称轴22x a a=<+故()h x在[2,3]a a++上单调递增min()(2)44h x h a a∴=+=-，max()(3)96h x h a a=+=-…………6分（1）若125a=，则96219()2525h x≤≤111252525219961log log()log02525h x∴-<≤≤<()()1f xg x∴-<………………………………………………9分（2）由题意，30x a->在[2,3]a a++上恒成立，则2301a a a+->⇒<又01a a>≠且0<<1a∴……………………………………………………12分4log(44)1599log(96)11212aaa aa a a⎧-≤⇒≤⎪⎪⎨⎪-≥-⇒≤≥⎪⎩…………16分故0a<≤18分。

人教版一年级数学上册期末摸底考试及答案(三篇)目录：人教版一年级数学上册期末摸底考试及答案一人教版一年级数学上册期末标准测试卷及答案二人教版一年级数学上册期末检测卷及答案三人教版一年级数学上册期末摸底考试及答案一班级：姓名：满分：100分考试时间：90分钟题序一二三四五总分得分一、我会算。

（20分）20+30= 45+8= 68－50= 96—6= 25+60=53—8= 82—7= 91+6= 24—8= 8+36=34+52= 40+16= 67—30= 84—40= 7+50=32+6+9= 21-3+50= 60+30-10= 27-6-3=7+17-6= 55+30-4= 29+60+8= 92-5-9=二、填空题。

（20分）1、4个一和2个十合起来是（_____）。

100里面有（_____）个十。

2、在里填上“＜”、“＞”或“＝”。

17－816－7 28－814＋7 66＋9 78－45＋4959+7 84－598－20 23+9 35－71元5角17角76－458＋6 2元＋3角32角3、做加法时,个位相加满（______）,要向十位进（______）;做减法时,个位不够减,要从（______）借1当（______）再减。

4、17是由（______）个十和（______）个一组成的。

5、把折成一个正方体，数字“6”的对面是数字（_______）。

6、2 元 5 角=（____）角 48 角=（____）元（____）角 1 元=（____）分7、和9相邻的两个数是（_____）和（_____）。

8、最小的四位数是（____），最大的三位数是（____），它们相差（____）。

9、我的个位是5，十位比个位少4，我是________。

10、比53小，比48大的单数有（______）和（______）。

三、选择题。

（10分）1、下面得数是5的算式是（）。

A．2+1 B．2+2 C．4+1 D．1+32、小光第一次剪了7个五角星，第二次剪了9个五角星，又送给小江2个，他还有( )个五角星。

2024-2025学年一年级上册数学人教版期末模拟试卷学校:___________姓名：___________班级：___________考号：___________一．填空题（1）看图写数。

（2）在横线上填上合适的数。

（1）15 前面一个数是 ，后面一个数是 。

（2）十位上是 1 ，个位上是 5 的数是 。

（3）18 里面有 个十和 个一。

（3）9个一和1个十合起来是 。

（4）在里填上“>”“<”或“=”。

7 5 2 5 6 4 97 445+38 69-3-5 2+4-60 3+3-27（5）小朋友们排队去公园，从左往右数小胖排的第6个，从右往左数小胖排在第4个，一共有 个小朋友去公园。

（6）一共有 个物体，其中正方体有 个，圆柱有 个，长方体有 个。

（7）在12和14中间的数是 ；被减数是14，减数是3，差是 ．（8）比9多5的数是 ，比18少8的数是 。

二．选择题（9）小黑和小白有同样多的鱼。

小黑吃了3条，小白吃了5条。

（ ）剩下的鱼多。

A．小黑B．小白（10）下列立体图形中，在桌面上放不稳的是（ ）A．球B．正方体C．长方体（11）如图：在这个13数中，左边的“1”表示（ ）。

A．1根小棒B．1个十C．1个一（12）□前面的一个数是14。

□内应填（ ）。

A．16B．13C．15（13）被减数是13，减数是1，差是（ )。

A．12B．14C．15（14）与7+8的结果相同的是（ ）A．8+7B．9+5C．17﹣4三．计算题（15）直接写出得数4+4＝5﹣3＝6+2＝7﹣4＝0+6＝9+4＝9﹣0＝10﹣9＝6+4＝8+5＝4+7＝8﹣6＝10+7＝15﹣10＝14﹣2＝9+8＝18﹣4＝6-3＝10﹣6＝16﹣6＝4+2+6＝9﹣7+5＝14﹣4+8＝16﹣3﹣2＝10−1+7＝8+3+6＝（16）根据指定的数画珠子（1）（2）四．看图计算（17）（18）（19）（个）（20）五．动手实践（21）把能站稳的那一组圈起来。