大同市口泉中学2014-2015学年高三上学期摸底考试

山西省大同市实验中学2023届高三上学期高考考前模拟（二）数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．设集合{}02,{1}A xx B x x =≤≤=>∣∣，则A B =I （ ） A ．(],1-∞ B ．(]1,2 C ．(],2-∞ D ．[]0,22．若复数z 满足()()2+323i z z z z +-=+，则z =（ ） A ．11i 22+B ．11i 22-C ．22i +D ．22i -3．ABC V 中，90C ∠=︒，2AC =，P 为线段BC 上任一点，则AP AC ⋅=u u u r u u u r（ ）A ．8B ．4C ．2D ．64．“01t <<”是“曲线2211x y t t +=-表示椭圆”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5．回文联是我国对联中的一种.用回文形式写成的对联，既可顺读，也可倒读.不仅意思不变，而且颇具趣味.相传，清代北京城里有一家饭馆叫“天然居”，曾有一副有名的回文联：“客上天然居，居然天上客；人过大佛寺，寺佛大过人.”在数学中也有这样一类顺读与倒读都是同一个数的自然数，称之为“回文数”.如44，585，2662等；那么用数字1，2，3，4，5，6可以组成4位“回文数”的个数为（ ） A ．30B ．36C ．360D ．12966．过圆2264x y +=上的动点作圆22:16C x y +=的两条切线，两个切点之间的线段称为切点弦，则圆C 不在任何切点弦上的点形成的区域的面积为（ ） A ．4πB ．6πC ．8πD ．12π7．我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，...，9填入33⨯的方格内，使三行、三列、两对角线的三个数之和都等于15 (如图）.一般地，将连续的正整数1，2，3，…，2n 填入n n ⨯的方格内，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n 阶幻方.记n 阶幻方的一条对角线上数的和为n N (如：在3阶幻方中，315N =)，则10N =A ．1020B ．1010C ．510D ．5058．若关于x 的方程22e ln (eln )0()x a x x x a ++=∈R 有两个不相等的实数根，则a 的取值范围是（ ） A ．(,2)(2,)-∞-+∞U B ．(,2][2,)-∞-+∞U C ．(2,2)-D ．[2,2]-二、多选题9．“中国最具幸福感城市调查推选活动”由新华社《瞭望东方周刊》、瞭望智库共同主办，至今已连续举办15年，累计推选出80余座幸福城市，现某城市随机选取30个人进行调查，得到他们的收入、生活成本及幸福感分数（幸福感分数为0~10分），并整理得到散点图（如图），其中x 是收入与生活成本的比值，y 是幸福感分数，经计算得回归方程为 1.50114ˆ.51x y=+.根据回归方程可知（ ）A ．y 与x 成正相关B ．样本点中残差的绝对值最大是2.044C ．只要增加民众的收入就可以提高民众的幸福感D ．当收入是生活成本3倍时，预报得幸福感分数为6.04410．已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称，则（ ）A ．函数12f x π⎛⎫+ ⎪⎝⎭为奇函数B ．函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增C ．函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像关于6x π=对称，则a的最小值是3π D ．若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ，则12x x -的最大值为2π11．定义在R 上的偶函数()f x 满足()()1232f x f x +=-，当[]0,2x ∈时，()2f x x =-，设函数()()2e26x g x x --=-<<，则（ ）A ．函数()f x 图象关于直线2x =对称B ．函数()f x 的周期为6C ．()()202320221f f +=-D ．()f x 和()g x 的图象所有交点横坐标之和等于812．如图，已知正方体1111ABCD A B C D -顶点处有一质点Q ，点Q 每次会随机地沿一条棱向相邻的某个顶点移动，且向每个顶点移动的概率相同．从一个顶点沿一条棱移动到相邻顶点称为移动一次．若质点Q 的初始位置位于点A 处，记点Q 移动n 次后仍在底面ABCD 上的概率为n P ，则下列说法正确的是（ ）A ．259P =B ．12133n n P P +=+ C ．点Q 移动4次后恰好位于点1C 的概率为0D ．点Q 移动10次后仍在底面ABCD 上的概率为10111()232+三、填空题13．已知0,0a b >>，若不等式313ma b a b+≥+恒成立，则m 的最大值为________．14．P 是抛物线28y x =上的动点，P 到y 轴的距离为1d ，到圆22:(3)(3)4C x y ++-=上动点Q 的距离为2d ，则12d d +的最小值为________．15．已知四面体ABCD ，平面ABD ⊥平面ABC ，DB BC ⊥，1DA DB ==，120ADB ∠=︒，且四面体ABCD 外接球的表面积为36π，则四面体ABCD 的体积为______．16．如图，一建筑工地有墙面α与水平面β垂直并交于l ，长为α内一点A 与平面β内一点B ，点,A B 距l 均为3米，,E F 分别为AB 的三等分点，若在平面α内一点P 向点,E F 连绳子，则PE PF +的最短长度为__________米.四、解答题17．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知cos 2cos 2cos A C c aB b--=.（1）求sin sin AC的值 （2）若1cos 4B =，b ＝2，求△ABC 的面积S . 18．从①12n a S n n ⎛⎫=+ ⎪⎝⎭；②23S a =，412a a a =；③12a =，4a 是2a ，8a 的等比中项这三个条件中任选一个，补充到下面横线上，并解答．已知等差数列{}n a 的前n 项和为n S ，公差d 不等于零，______． (1)求数列{}n a 的通项公式；(2)若122n n n b S S +=-，数列{}n b 的前n 项和为n W ，求n W ．19．如图，在四棱锥E -ABCD 中，平面ADE ⊥平面ABCD ，O ､M 分别为线段AD ､DE 的中点，四边形BCDO 是边长为1的正方形，AE =DE ，AE ⊥DE.(1)求证：CM //平面ABE ；(2)求直线CM 与BD 所成角的余弦值；(3)点N 在直线AD 上，若平面BMN ⊥平面ABE ，求线段AN 的长.20．某工厂两条生产线分别生产甲、乙两种元件，元件质量按测试指标划分为：指标大于或等于76为正品，小于76为次品.现分别从两条生产线随机抽取元件甲和元件乙各100件进行检测，检测结果统计如下：(1)试分别估计生产一件元件甲、一件元件乙为正品的概率；(2)生产一件元件甲，若是正品则盈利90元，若是次品则亏损10元；生产一件元件乙，若是正品则盈利100元，若是次品则亏损20元，则在（1）的前提下： ①求生产5件元件乙所获得的利润不少于300的概率；②记X ，Y 分别为生产1000件元件甲和1000件元件乙所得的总利润，试比较()E X 和()E Y 的大小.（结论不要求证明）21．已知函数()21e 2x f x ax =-，其中a R ∈．(1)若函数()f x 在()0,∞+上单调递增，求a 的取值范围； (2)若函数()f x 存在两个极值点1x ，()212x x x <，[]212,e ∈x x 时，求12x x +的取值范围. 22．已知椭圆C 的方程为22142x y +=，过点203Q ⎛⎫ ⎪⎝⎭，作直线与椭圆交于A ，B 两点.（1）求证：P A ⊥PB ；（2）求|P A|·|PB|的最大值.。

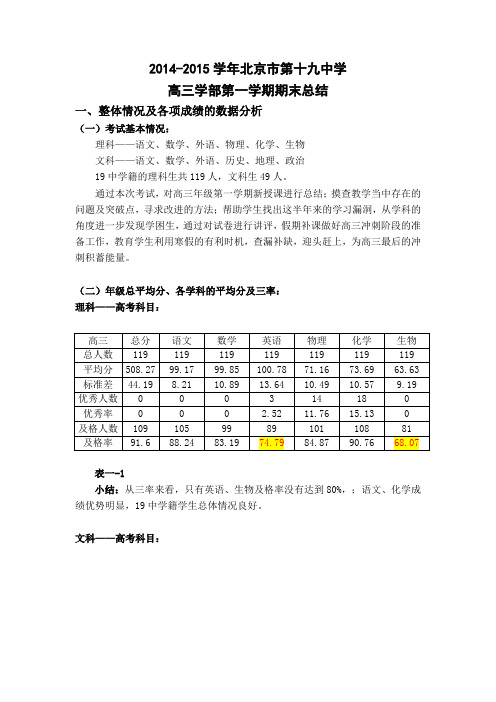
2014-2015学年北京市第十九中学高三学部第一学期期末总结一、整体情况及各项成绩的数据分析（一）考试基本情况：理科——语文、数学、外语、物理、化学、生物文科——语文、数学、外语、历史、地理、政治19中学籍的理科生共119人，文科生49人。

通过本次考试，对高三年级第一学期新授课进行总结；摸查教学当中存在的问题及突破点，寻求改进的方法；帮助学生找出这半年来的学习漏洞，从学科的角度进一步发现学困生，通过对试卷进行讲评，假期补课做好高三冲刺阶段的准备工作，教育学生利用寒假的有利时机，查漏补缺，迎头赶上，为高三最后的冲刺积蓄能量。

（二）年级总平均分、各学科的平均分及三率：理科——高考科目：表一-1小结：从三率来看，只有英语、生物及格率没有达到80%，；语文、化学成绩优势明显，19中学籍学生总体情况良好。

文科——高考科目：表一-2小结：从三率来看，语文、英语、地理学科成绩优势明显，政治、数学有两级分化的趋势。

（三）期中期末各科成绩比较：理科：高二期末高三期中高三期末表二——1小结：与高三期中成绩相比，从三率来看，各学科成绩略有变化，总体上看各科成绩在全区的排名较好，物理、化学学科优秀率较高，语文、数学、英语学科成绩稳定，只有生物学科出现了个别的低分学生。

文科：高二期末高三期中高三期末表二——2小结：与上学期末成绩相比，语文、数学、英语学科成绩优势明显，在及格率方面，语文为100%，英语、历史、地理的及格率也非常好。

数学、政治学科有学生出现两极分化现象。

（四）期末实验班、普通班、特长班成绩（以下统计以19中学籍学生为主）：理科：普通班2班479.0695.8596.5997.7464.416658.47普通班3班486.0397.9796.6194.9466.6169.8960普通班8班481.8896.595.191.2866.8569.9562.2普通班平均481.0896.4994.8694.8166.4068.5359.99年级平均差-27.19-2.68-4.99-5.97-4.77-5.16-3.64表三-1小结：实验班的成绩优势明显，尤其是英语、数学、生物成绩突出；普通班的成绩发展比较均衡，其中语文、物理、生物较好。

山西省大同市口泉中学2025届高考冲刺模拟数学试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．某几何体的三视图如图所示，其中正视图是边长为4的正三角形，俯视图是由边长为4的正三角形和一个半圆构成，则该几何体的体积为（ ）A ．4383π+B ．2383π+C ．4343π+D ．8343π+2．已知定点1(4,0)F -，2(4,0)F ，N 是圆22:4O x y +=上的任意一点，点1F 关于点N 的对称点为M ，线段1F M 的垂直平分线与直线2F M 相交于点P ，则点P 的轨迹是（ ） A ．椭圆B ．双曲线C ．抛物线D ．圆3．已知0a >，若对任意()0,m ∈+∞，关于x 的不等式()()1e ln 11exaxx m m --<-+-（e 为自然对数的底数）至少有2个正整数解，则实数a 的取值范围是（ ）A ．3e e,2e ⎛⎤+ ⎥⎝⎦B ．3e ,2e ⎡⎫++∞⎪⎢⎣⎭C ．3e 0,2e ⎛⎤+ ⎥⎝⎦D ．3e ,2e ⎛⎫++∞ ⎪⎝⎭4．已知函数ln(1),0()11,02x x f x x x +>⎧⎪=⎨+≤⎪⎩，若m n <,且 ()()f m f n =，则n m -的取值范围为（ ）A ．[32ln 2,2)-B ．[32ln 2,2]-C ．[1,2)e -D ．[1,2]e -5．若函数()()222cos 137f x x x m x m m =+-+++-有且仅有一个零点，则实数m 的值为（ ）A 337--B 337-+ C ．4- D ．26．一个几何体的三视图及尺寸如下图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的表面积是 （ ）A ．16216πB ．1628πC ．8216πD ．828π7．已知双曲线221x y a+=的一条渐近线倾斜角为56π，则a =（ ）A ．3B ．3-C ．3D ．3-8．设复数z 满足31ii z=+，则z =（ ）A ．1122i + B ．1122-+i C ．1122i - D ．1122i -- 9．各项都是正数的等比数列{}n a 的公比1q ≠，且2311,,2a a a 成等差数列，则3445a a a a ++的值为( ) A 15-B 51+ C 51- D 51+51-10．已知双曲线22221(0,0)x y a b a b-=>>的离心率为e ，抛物线22(0)y px p =>的焦点坐标为(1,0)，若e p =，则双曲线C 的渐近线方程为（ ） A ．3y x =± B ．22y x =± C ．52y x =±D ．22y x =±11．已知0,2πα⎛⎫∈ ⎪⎝⎭，0,2πβ⎛⎫∈ ⎪⎝⎭，cos2tan 1sin 2βαβ=-，则（ ） A ．22παβ+=B ．4παβ+=C ．4αβ-=πD ．22παβ+=12．执行如图所示的程序框图，若输入的3t =，则输出的i =( )A ．9B ．31C ．15D ．63二、填空题：本题共4小题，每小题5分，共20分。

山西省大同市口泉中学2024届高三高考全真模拟卷（七）英语试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

第一部分（共20小题，每小题1.5分，满分30分）1．Lucia impressed her peer students with her musical talent, as well as several foreign languages ______.A．on her own B．under her control C．in her charge D．at her command2．Mr. Zhang gave all textbooks to all the pupils, except ____________ who had already taken them.A．these B．onesC．those D．the others3．If it ________ for her great help then, I would not study English so well now.A．hasn’t been B．wasn’tC．hadn’t been D．isn’t4．Anna was in Inner Mongolia for two years, ____ as a volunteer teacher.A．having worked B．working C．worked D．to work5．Usually doctors are understandably ________ about new medicines because of the uncertainty of their effects.A．considerate B．logical C．optimistic D．cautious6．—Hi, Tom, have you checked the account yet?—Certainly, I ________ it five times even though you told me to do it twice.A．checked B．will have checkedC．have been checking D．had checked7．________ amazed us greatly was that Linda could speak five languages.A．That B．What C．Which D．Why8．—What about going abroad for further study?—Great, but I never expected ______ a chance for me before.A．there to be B．there beingC．it to be D．it being9．After the argument Colin ran away and______since.A．Isn’t heard of B．wasn’t heard ofC．hasn’t been heard of D．hadn’t been hear d of10．The Games are known as the friendly games because of their ________ on kindness and mutual respect.A．lacks B．focusesC．challenges D．researches11．for years of hard training, she would not be standing on the stage, receiving huge cheers and applause. A．It were not B．It had not beenC．Were it not D．Had it not been.12．The teacher told the children ______ quiet in the museum.A．keep B．kept C．keeping D．to keep13．—I wonder why he has been acting so strangely these days．—Recent pressure at work may ____ his behavior．A．account for B．call for C．change for D．stand for14．The shocking news made me realize ________ terrible problems we would face.A．what B．howC．that D．why15．— How is the test that you took yesterday?— Unfortunately, not even one of the hundred students who took the test ______ passed.A．has B．have C．are D．is16．—Our team has just narrowly won the game. I feel so relieved now.—__________!A．Cheer up B．Y ou betC．What a pity D．Well done17．Sh e doesn’t speak our language, _____ she seems to understand what we say．A．for B．and C．yet D．or18．—It’s so humid these days!—Don’t worry! The rain ________ to stop from tomorrow.A．will expect B．expectsC．will be expected D．is expected19．—Let’s go and have dinner this evening.—_____. Have you come out first in the exam?A．Thanks a lot. B．Why not?C．What for? D．Yes, I’d like to.20．—I’m terribly sorry. I’m late because ….—That’s OK. You are here and that’s what _____.A．does B．works C．functions D．counts第二部分阅读理解（满分40分）阅读下列短文，从每题所给的A、B、C、D四个选项中，选出最佳选项。

山西省大同市高三年级第一次模拟考试文科综合能力测试第I卷选择题24．《荀子•富国》记载：“今是土之生五谷也，人善治之，则亩益数盆，一岁而再获之。

”荀子在这里强调的是A．要重视农业生产精耕细作技术的提商 B．要及吋播种、除草、灌溉C．要多种植五谷，才能获得丰收 D．要年年种植五谷，改良土壤25．唐朝诗人孟郊的《登科后》诗：“春风得意马蹄疾，一朝看遍长安花”，反映了士子在参加完科考获取功名后的心情。

据此判断这位士子参加的是A．贡试 B．乡试 C．会试 D．殿试26．罗马的斯多亚哲学家塞内卡说：“奴隶是人，他们的天性和其他人相同，奴隶的灵魂中，同样有其他人所具有的自豪、荣誉、勇敢和高尚那些品性，不管他们的社会地位如何。

下列理解不正确的是A．斯多亚学派论证了天赋人权、人生而平等的思想B．斯多亚学派为罗马法的形成创造了一些条件C．斯多亚学派反对奴隶制度D．与儒家哲学一样具有朴素的人道主义色彩27．仔细分析下列三幅图，可以看出我国古代商业城市发展变化的规律是A．由北方的黄河中下游地区逐渐向南方、向沿海和运河地区发展B．由中原地区向整个沿海地区发展C．由北方地区向边疆地区发展D．由黄河中下游地区向全国各个地区发展28．“再涝地熟，旱亦保泽”。

黄河中下游地区，气候干燥，降水少，蒸发量大，严重影响了播种和农作物生长。

为解决这一难题，魏晋南北朝时期发明了A．水稻育秧移栽技术 B．耕耙耱技术 C．代田法 D．筒车29．德国天主教祌学家席林（1874—1956）认为，为了给人类的生存提供物质资料，人类必须从事经济活动，但是经济活动不是目的本身，毋宁说“最终的目的是为了上帝”，这是当时天主教经济伦理学的基本观点之一。

以下是对这一观点的分析，合理的是A．己经脱离了社会发展实际 B．是宗教顺应了时代的表现C．成了福利国家的理论甚础 D．挑战了西方国家社会形态30．下图的《19世纪欧美主要国家城市和农村人口统计表》说明了①工业化程度越低的国家农村人口比例越大②国际联合企业和跨国公司的出现推动了人口的流动③工业革命促进人口向城市迁移④除英国外其他国家还没有开始工业化的进程A．①③ B．①②③④ C．②③ D．①②④31．19世纪60年代，清政府批准成立的某机构“一切均仿照军机处办理”。

2014-2015学年山西省大同一中、同煤一中联考高三（上）期末数学试卷（理科）一、选择题：（每小题5分，共60分．）1．（5分）已知集合A={x|log4x＜1}，B={x|x≥2}，则A∩∁RB=（）A．（﹣∞，2）B．（0，2）C．（﹣∞，2] D．[2，4）【考点】：交、并、补集的混合运算．【专题】：计算题．【分析】：求出A中其他不等式的解集确定出A，根据全集R及B求出B的补集，找出A与B 补集的交集即可．【解析】：解：由A中的不等式变形得：log4x＜1=log44，得到0＜x＜4，即A=（0，4）；∵B=[2，+∞），全集为R，∴∁RB=（﹣∞，2），则A∩∁RB=（0，2）．故选B【点评】：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．2．（5分）若复数z满足（3﹣4i）z=|4+3i|，则z的虚部为（）A．﹣4 B．C．4 D．【考点】：复数代数形式的乘除运算；复数求模．【专题】：数系的扩充和复数．【分析】：由题意可得z==，再利用两个复数代数形式的乘除法法则化简为+i，由此可得z的虚部．【解析】：解：∵复数z满足（3﹣4i）z=|4+3i|，∴z====+i，故z的虚部等于，故选：D．【点评】：本题主要考查复数的基本概念，两个复数代数形式的乘除法法则的应用，属于基础题．3．（5分）已知a＞0且a≠1，函数y=logax，y=ax，y=x+a在同一坐标系中的图象可能是（）A．B．C．D．【考点】：函数的图象．【专题】：函数的性质及应用．【分析】：根据指数函数和对数的函数的单调性，和一次函数的纵截距所得的a的范围是否一致．故可判断．【解析】：解：当0＜a＜1，y=logax，y=ax均为减函数，且y=x+a与y轴的交点纵坐标小于1，当a＞1，y=logax，y=ax均为增函数，且y=x+a与y轴的交点纵坐标大于于1，观察图象知，A，B，D均错，只有C正确．故选：C【点评】：本小题主要考查，一次函数，对数函数、指数函数的图象等基础知识，考查数形结合思想．属于基础题．4．（5分）设x，y满足约束条件，则取值范围是（）A．[1，5] B．[2，6] C．[3，10] D．[3，11]【考点】：简单线性规划的应用．【专题】：计算题；数形结合．【分析】：再根据约束条件画出可行域，利用几何意义求最值，只需求出直线l0过A（0，4）时l0最大，k也最大为11，当直线l0过B（0，0））时l0最小，k也最小为3即可．【解析】：解：根据约束条件画出可行域，∵设k==1+，整理得（k﹣1）x﹣2y+k﹣3=0，由图得，k＞1．设直线l0=（k﹣1）x﹣2y+k﹣3，当直线l0过A（0，4）时l0最大，k也最大为11，当直线l0过B（0，0））时l0最小，k也最小为3．故选D．【点评】：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．5．（5分）在等差数列{an}中，有3（a3+a5）+2（a7+a10+a13）=48，则此数列的前13项和为（）A．24 B．39 C．52 D．104【考点】：等差数列的前n项和；等差数列的通项公式．【专题】：计算题．【分析】：利用等差数列的性质可把3（a3+a5）+2（a7+a10+a13）=48，化简6a4+6a10=48，从而可a1+a13=a4+a10=8而，从而可求【解析】：解：∵3（a3+a5）+2（a7+a10+a13）=48，利用等差数列的性质可得，6a4+6a10=48∴a1+a13=a4+a10=8∴故选C【点评】：本题主要考查了等差数列的性质和数列的求和．解题的关键是利用了等差数列的性质：若m+n=p+q，则am+an=ap+aq．6．（5分）已知函数f（x）=sin（x﹣φ），且f（x）dx=0，则函数f（x）的图象的一条对称轴是（）A．x=B．x=C．x=D．x=【考点】：函数y=Asin（ωx+φ）的图象变换；定积分．【专题】：三角函数的图像与性质．【分析】：由f（x）dx=0求得cos（φ+）=0，故有φ+=kπ+，k∈z．可取φ=，则f（x）=sin（x﹣）．令x﹣=kπ+，求得x的值，可得函数f（x）的图象的一条对称轴方程．【解析】：解：∵函数f（x）=sin（x﹣φ），f（x）dx=﹣cos（x﹣φ）=﹣cos（﹣φ）﹣[﹣cos（﹣φ）]=cosφ﹣sinφ=cos （φ+）=0，∴φ+=kπ+，k∈z，即φ=kπ+，k∈z，故可取φ=，f（x）=sin（x﹣）．令x﹣=kπ+，求得x=kπ+，k∈Z，则函数f（x）的图象的一条对称轴为x=，故选：A．【点评】：本题主要考查定积分，函数y=Asin（ωx+φ）的图象的对称性，两角和差的三角公式的应用，属于中档题．7．（5分）如图所示，用过A1、B、C1和C1、B、D的两个截面截去正方体ABCD﹣A1B1C1D1的两个角后得到一个新的几何体，则该几何体的正视图为（）A．B．C．D．【考点】：简单空间图形的三视图．【专题】：计算题；空间位置关系与距离．【分析】：直接利用三视图的定义，正视图是光线从几何体的前面向后面正投影得到的投影图，据此可以判断出其正视图．【解析】：解：由正视图的定义可知：点A、A1、C1在后面的投影点分别是点D、D1、C1，线段A1B在后面的投影面上的投影是以D1为端点且与线段A1B平行且相等的线段，即可得正视图．故选：A．【点评】：从正视图的定义可以判断出题中的正视图，同时要注意能看见的轮廓线和棱用实线表示，不能看见的轮廓线和棱用虚线表示．8．（5分）已知非零向量与满足且=．则△ABC为（）A．等边三角形B．直角三角形C．等腰非等边三角形D．三边均不相等的三角形【考点】：三角形的形状判断．【专题】：计算题．【分析】：通过向量的数量积为0，判断三角形是等腰三角形，通过=求出等腰三角形的顶角，然后判断三角形的形状．【解析】：解：因为，所以∠BAC的平分线与BC垂直，三角形是等腰三角形．又因为，所以∠BAC=60°，所以三角形是正三角形．故选A．【点评】：本题考查向量的数量积的应用，考查三角形的判断，注意单位向量的应用，考查计算能力．9．（5分）已知双曲线=1（a＞0，b＞0）的左、右焦点分别为Fl，F2，以|F1F2|为直径的圆与双曲线渐近线的一个交点为（3，4），则此双曲线的方程为（）A．B．C．D．【考点】：双曲线的简单性质．【专题】：计算题；圆锥曲线的定义、性质与方程．【分析】：根据题意，点（3，4）到原点的距离等于半焦距，可得a2+b2=25．由点（3，4）在双曲线的渐近线上，得到=，两式联解得出a=3且b=4，即可得到所求双曲线的方程．【解析】：解：∵点（3，4）在以|F1F2|为直径的圆上，∴c==5，可得a2+b2=25…①又∵点（3，4）在双曲线的渐近线y=上，∴=…②，①②联解，得a=3且b=4，可得双曲线的方程故选：C【点评】：本题给出双曲线满足的条件，求双曲线的方程，考查了双曲线的标准方程与简单几何性质等知识，属于中档题．10．（5分）已知m、n表示两条不同直线，α表示平面．下列四个命题中，正确的个数是（）①若m∥α，n∥α，则m∥n②若m⊥α，n⊂α，则m⊥n③若m⊥α，m⊥n，则n∥α④若m∥α，m⊥n，则n⊥αA． 4 B．3 C． 2 D．1【考点】：空间中直线与平面之间的位置关系．【专题】：空间位置关系与距离．【分析】：利用线面平行、线面垂直的性质定理和判定定理解答．【解析】：解：对于①，若m∥α，n∥α，则m与n平行、相交或者异面；故①错误；对于②，若m⊥α，n⊂α，根据线面垂直的性质可得m⊥n；故②正确；对于③，若m⊥α，m⊥n，则n∥α或者n⊂α内；故③错误；对于④，若m∥α，m⊥n，则n⊥α或者n⊂α；故D错误；故选D．【点评】：本题考查了线面平行、线面垂直的性质定理和判定定理的运用；关键是熟练有关的定理，正确运用．11．（5分）设α∈（0，），β∈（0，），且tanα=，则（）A．3α﹣β=B．3α+β=C．2α﹣β=D．2α+β=【考点】：三角函数的化简求值．【专题】：三角函数的求值．【分析】：化切为弦，整理后得到sin（α﹣β）=cosα，由该等式左右两边角的关系可排除选项A，B，然后验证C满足等式sin（α﹣β）=cosα，则答案可求．【解析】：解：由tanα=，得：，即sinαcosβ=cosαsinβ+cosα，sin（α﹣β）=cosα．由等式右边为单角α，左边为角α与β的差，可知β与2α有关．排除选项A，B后验证C，当时，sin（α﹣β）=sin（）=cosα成立．故选：C．【点评】：本题考查三角函数的化简求值，训练了利用排除法及验证法求解选择题，是基础题．12．（5分）已知函数f（x）=2lnx+1的图象与直线y=2x﹣a恰好有一个交点，设g（x）=ex﹣x2+a，当x∈[1，2]时，不等式﹣m≤g（x）≤m2﹣4恒成立，则实数m的取值范围是（）A．（﹣∞，] B．[，e] C．[﹣e，] D．[，+∞）【考点】：函数恒成立问题．【专题】：导数的综合应用．【分析】：用导数求出曲线上某点切线方程，即可得到a的值，再利用导数求出函数g（x）=ex﹣x2+a，当x∈[1，2]时的最值，再根据不等式﹣m≤g（x）≤m2﹣4恒成立，求的m的范围【解析】：解：∵函数f（x）=2lnx+1的图象与直线y=2x﹣a恰好有一个交点，∴直线y=2x﹣a与f（x）相切设曲线的切点为P（x0，y0），∵f′（x）=，∴f′（x0）==2，∴x0=1，∴y0=2lnx0+1=1，∴2﹣a=1，∴a=1∴g（x）=ex﹣x2+1，∴g′（x）=ex﹣2x，x∈[1，2]设h（x）=ex﹣2x，x∈[1，2]∴h′（x）=ex﹣2＞0在[1，2]恒成立，∴h（x）=ex﹣2x，x∈[1，2]为增函数，∴h（x）min=h（1）=e﹣2＞0，∴g′（x）＞0在[1，2]恒成立，∴g（x）=ex﹣x2+1在[1，2]为增函数，∴g（1）≤g（x）≤g（2），即e≤g（x）≤e2﹣3∵当x∈[1，2]时，不等式﹣m≤g（x）≤m2﹣4恒成立∴解得m≥故选：D．【点评】：本题考查了导数和函数的最值的关系，以及导数的集合意义，以及恒成立的问题，属于中档题二、填空题（每小题5分，共20分）13．（5分）已知sin（﹣x）=，则sin2x的值为．【考点】：二倍角的正弦；两角和与差的正弦函数．【专题】：计算题．【分析】：利用诱导公式和两角和公式对sin2x化简整理，然后把sin（﹣x）=代入即可得到答案．【解析】：解：sin2x=cos（﹣2x）=1﹣2sin2（﹣x）=故答案为【点评】：本题主要考查了三角函数中的二倍角公式．属基础题．14．（5分）已知A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为．【考点】：平面向量数量积的含义与物理意义；平面向量数量积的运算．【专题】：计算题；平面向量及应用．【分析】：根据点的坐标，分别算出=（5，5）、=（2，1），从而算出=15且||=5．再利用向量投影的公式加以计算，即可得到向量在方向上的投影的值．【解析】：解：∵C（﹣2，﹣1），D（3，4），∴=﹣=（5，5），同理可得=﹣=（2，1），∴=5×2+5×1=15，==5设、的夹角为α，则向量在方向上的投影为||cosα===故答案为：【点评】：本题给出A、B、C、D各点的坐标，求向量在方向上的投影．着重考查了平面向量的坐标运算、数量积的公式及其运算性质和向量投影的概念等知识，属于中档题．15．（5分）已知函数，若f（3﹣a2）＜f（2a），则实数a的取值范围是﹣3＜a＜1．【考点】：函数单调性的性质．【专题】：函数的性质及应用．【分析】：根据分段函数的解析式判断出函数的单调性，利用函数的单调性去掉“f”，转化为关于a的不等式，求解即可得到a的取值范围．【解析】：解：∵函数，作出分段函数的图象如图所示，∴根据函数的图象可得，函数f（x）在定义域R上是单调递减函数，∵f（3﹣a2）＜f（2a），∴3﹣a2＞2a，即a2+2a﹣3＜0，∴﹣3＜a＜1，实数a的取值范围是﹣3＜a＜1．故答案为：﹣3＜a＜1．【点评】：本题考查了分段函数的图象，对于分段函数的问题，一般选用分类讨论和数形结合的思想方法进行求解．利用基本初等函数的单调性判断函数的单调性，运用了函数的单调性解不等式，解题的关键是将不等式进行合理的转化，然后利用单调性去掉“f”．属于中档题．16．（5分）如图，已知点F为抛物线C：y2=4x的焦点，点P是其准线l上的动点，直线PF 交抛物线C于A、B两点．若点P的纵坐标为m（m≠0），点D为准线l与x轴的交点，则△DAB 的面积S的取值范围为（4，+∞）．【考点】：抛物线的简单性质．【专题】：解三角形；圆锥曲线的定义、性质与方程．【分析】：由抛物线C：y2=4x可得焦点F（1，0）．设A（x1，y1），B（x2，y2），直线PF的方程为：y=k（x﹣1）．与抛物线方程联立可得：k2x2﹣（2k2+4）x+k2=0，利用根与系数的关系和弦长公式，求出点D（﹣1，0）到直线AB的距离d．再利用S△DAB=d•|AB|，即可得出所求范围．【解析】：解：由抛物线C：y2=4x可得焦点F（1，0）．设A（x1，y1），B（x2，y2），直线PF的方程为：y=k（x﹣1）．联立，化为k2x2﹣（2k2+4）x+k2=0，则x1+x2=2+，x1x2=1．∴|AB|=•=•=．点D（﹣1，0）到直线AB的距离d=．∴S△DAB=d•|AB|=•=4＞4．∴△DAB的面积S的取值范围为（4，+∞）．故答案为：（4，+∞）．【点评】：本题考查了直线与抛物线相交问题转化为方程联立，同时考查根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式，考查了推理能力与计算能力，属于中档题．三、解答题（解答应写出文字说明、证明过程或演算步骤）17．（12分）如图，在平面四边形ABCD中，AD=1，CD=2，AC=．（Ⅰ）求cos∠CAD的值；（Ⅱ）若cos∠BAD=﹣，sin∠CBA=，求BC的长．【考点】：解三角形的实际应用．【专题】：解三角形．【分析】：（Ⅰ）利用余弦定理，利用已知条件求得cos∠CAD的值．（Ⅱ）根据cos∠CAD，cos∠BAD的值分别，求得sin∠BAD和sin∠CAD，进而利用两角和公式求得sin∠BAC的值，最后利用正弦定理求得BC．【解析】：解：（Ⅰ）cos∠CAD===．（Ⅱ）∵cos∠BAD=﹣，∴sin∠BAD==，∵cos∠CAD=，∴sin∠CAD==∴sin∠BAC=sin（∠BAD﹣∠CAD）=sin∠BADcos∠CAD﹣cos∠BADsin∠CAD=×+×=，∴由正弦定理知=，∴BC=•sin∠BAC=×=3【点评】：本题主要考查了正弦定理和余弦定理的综合运用，三角函数恒等变换的应用．考查了学生对基础知识的综合运用．18．（12分）设Sn为数列{an}的前n项和，已知a1≠0，2an﹣a1=S1•Sn，n∈N*（Ⅰ）求a1，a2，并求数列{an}的通项公式；（Ⅱ）求数列{nan}的前n项和．【考点】：等差数列与等比数列的综合；数列的求和．【专题】：等差数列与等比数列．【分析】：（Ⅰ）令n=1和2，代入所给的式子求得a1和a2，当n≥2时再令n=n﹣1得到2an ﹣1﹣1=Sn﹣1，两个式子相减得an=2an﹣1，判断出此数列为等比数列，进而求出通项公式；（Ⅱ）由（Ⅰ）求出nan=n•2n﹣1，再由错位相减法求出此数列的前n项和．【解析】：解：（Ⅰ）令n=1，得2a1﹣a1=，即，∵a1≠0，∴a1=1，令n=2，得2a2﹣1=1•（1+a2），解得a2=2，当n≥2时，由2an﹣1=Sn得，2an﹣1﹣1=Sn﹣1，两式相减得2an﹣2an﹣1=an，即an=2an﹣1，∴数列{an}是首项为1，公比为2的等比数列，∴an=2n﹣1，即数列{an}的通项公式an=2n﹣1；（Ⅱ）由（Ⅰ）知，nan=n•2n﹣1，设数列{nan}的前n项和为Tn，则Tn=1+2×2+3×22+…+n×2n﹣1，①2Tn=1×2+2×22+3×23+…+n×2n，②①﹣②得，﹣Tn=1+2+22+…+2n﹣1﹣n•2n=2n﹣1﹣n•2n，∴Tn=1+（n﹣1）2n．【点评】：本题考查了数列an与Sn之间的转化，以及由错位相减法求出数列的前n项和的应用．19．（12分）如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD ⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．【考点】：直线与平面垂直的性质；用空间向量求平面间的夹角．【专题】：计算题；证明题；综合题；数形结合；转化思想．【分析】：（Ⅰ）因为∠DAB=60°，AB=2AD，由余弦定理得BD=，利用勾股定理证明BD⊥AD，根据PD⊥底面ABCD，易证BD⊥PD，根据线面垂直的判定定理和性质定理，可证PA ⊥BD；（Ⅱ）建立空间直角坐标系，写出点A，B，C，P的坐标，求出向量，和平面PAB的法向量，平面PBC的法向量，求出这两个向量的夹角的余弦值即可．【解析】：（Ⅰ）证明：因为∠DAB=60°，AB=2AD，由余弦定理得BD=，从而BD2+AD2=AB2，故BD⊥AD又PD⊥底面ABCD，可得BD⊥PD所以BD⊥平面PAD．故PA⊥BD（Ⅱ）如图，以D为坐标原点，AD的长为单位长，射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz，则A（1，0，0），B（0，，0），C（﹣1，，0），P（0，0，1）．=（﹣1，，0），=（0，，﹣1），=（﹣1，0，0），设平面PAB的法向量为=（x，y，z），则即，因此可取=（，1，）设平面PBC的法向量为=（x，y，z），则，即：可取=（0，1，），cos＜＞==﹣，故二面角A﹣PB﹣C的余弦值为：﹣．【点评】：此题是个中档题．考查线面垂直的性质定理和判定定理，以及应用空间向量求空间角问题，查了同学们观察、推理以及创造性地分析问题、解决问题能力．20．（12分）如图，椭圆C：+=1（a＞b＞0）的离心率e=，短轴的两个端点分别为B1、B2，焦点为F1、F2，四边形F1B1F2B2的内切圆半径为．（1）求椭圆C的方程；（2）过左焦F1点的直线交椭圆于M、N两点，交直线x=﹣4于点P，设=λ，=μ，试证λ+μ为定值．【考点】：直线与圆锥曲线的综合问题．【专题】：圆锥曲线中的最值与范围问题．【分析】：（Ⅰ）设四边形F1B1F2B2的内切圆与边B2F2的切点为G，连接OG，则|OG|=．由利用等积法得bc=，e=，由此能求出椭圆C的方程．（Ⅱ）设直线MN的方程为y=k（x+1），代入椭圆方程，整理得（3+4k2）x2+8k2x+4（k2﹣3）=0．由此利用韦达定理结合已知条件能证明λ+μ=0为定值．【解析】：（Ⅰ）解：如图所示，设四边形F1B1F2B2的内切圆与边B2F2的切点为G，连接OG，则|OG|=．由==，|OB2|=b，|OF2|=c，|B2F2|=a，得bc=，又e=，a2=b2+c2，解得a=2，b=，故椭圆C的方程为．…（5分）（Ⅱ）证明：根据已知条件可设直线MN的方程为y=k（x+1），代入椭圆方程，整理得（3+4k2）x2+8k2x+4（k2﹣3）=0．设M（x1，y1），N（x2，y2），则．又P（﹣4，﹣3k），由，，得，．…（9分）∴λ+μ=﹣=﹣=﹣，∵2x1x2+5（x1+x2）+8=2•==0，∴λ+μ=0为定值．…（13分）【点评】：本题考查椭圆方程的求法，考查两数和为定值的证明，解题时要认真审题，注意函数与方程思想的合理运用．21．（12分）设函数f（x）=﹣x+alnx（a∈R）（e=2.71828…是一个无理数）．（1）若函数f（x）在定义域上不单调，求a的取值范围；（2）设函数f（x）的两个极值点分别为x1和x2，记过点A（x1，f（x1）），B（x2，f（x2））的直线斜率为k，若k≤•a﹣2恒成立，求a的取值集合．【考点】：利用导数研究函数的极值；利用导数研究函数的单调性．【专题】：导数的综合应用；不等式的解法及应用．【分析】：（1）求出导数，令g（x）=x2﹣ax+1，其判别式△=a2﹣4．讨论①当﹣2≤a≤2时，②当a＜﹣2时，③当a＞2时，由导数符号确定函数的单调性，即可得到a的范围；（2）运用韦达定理可得a=x1+x2=x2+＞2，作差f（x1）﹣f（x2），再由条件，结合恒成立思想，运用函数的单调性，构造函数F（x）=﹣x+•lnx（x＞1），通过求导，判断单调性可得x2≥e，即可得到a的范围．【解析】：解：（1）∵f（x）的定义域为（0，+∞），f′（x）=﹣﹣1+=﹣，令g（x）=x2﹣ax+1，其判别式△=a2﹣4．①当﹣2≤a≤2时，△≤0，f′（x）≤0，故f（x）在（0，+∞）上单调递减，不合题意．②当a＜﹣2时，△＞0，g（x）=0的两根都小于零，故在（0，+∞）上，f′（x）＜0，故f（x）在（0，+∞）上单调递减，不合题意．③当a＞2时，△＞0，设g（x）=0的两个根x1，x2都大于零，令x1=，x2=，x1x2=1，当0＜x＜x1时，f′（x）＜0，当x1＜x＜x2时，f′（x）＞0，当x＞x2时，f′（x）＜0，故f（x）分别在（0，x1），（x2，+∞）上单调递减，在（x1，x2）上单调递增，综上所述，a的取值范围是（2，+∞）．（2）依题意及（1）知，a=x1+x2=x2+＞2，∵f（x1）﹣f（x2）=﹣x1+alnx1﹣（﹣x2+alnx2）=+（x2﹣x1）+a（lnx1﹣lnx2），∴k==﹣﹣1+a•=﹣2+a•．若k≤•a﹣2，则﹣2+a•≤•a﹣2，∴≤，不妨设x1＜x2，则x1﹣x2≤（lnx1﹣lnx2）．又x1=，∴﹣x2≤（﹣2lnx2），∴﹣x2+lnx2≤0（x2＞1）①恒成立．记F（x）=﹣x+•lnx（x＞1），F′（x）=﹣﹣1+•，记x1′=[﹣]，x2′═[+]，由（1）③知F（x）在（1，x2′）上单调递增，在（x2′，+∞）上单调递减，且易知0＜x1′＜1＜x2′＜e．又F（1）=0，F（e）=0，所以，当x∈（1，e）时，F（x）＞0；当x∈[e，+∞）时，F（x）≤0．故由①式可得，x2≥e，代入方程g（x2）=x22﹣ax2+1=0，得a=x2+≥e+（∵a=x2+在x2∈[e，+∞）上递增）．又a＞2，所以a的取值集合是{a|a≥e+}．【点评】：本题考查导数的运用：求单调区间、极值，主要考查极值的运用，运用分类讨论的思想方法是解题的关键，同时考查函数的单调性的运用和基本不等式的运用，考查运算能力，属于难题．22．（10分）选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2，）．（1）求点A，B，C，D的直角坐标；（2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．【考点】：椭圆的参数方程；简单曲线的极坐标方程；点的极坐标和直角坐标的互化．【专题】：综合题；压轴题．【分析】：（1）确定点A，B，C，D的极坐标，即可得点A，B，C，D的直角坐标；（2）利用参数方程设出P的坐标，借助于三角函数，即可求得|PA|2+|PB|2+|PC|2+|PD|2的取值范围．【解析】：解：（1）点A，B，C，D的极坐标为点A，B，C，D的直角坐标为（2）设P（x0，y0），则为参数）t=|PA|2+|PB|2+|PC|2+|PD|2=4x2+4y2+16=32+20sin2φ∵sin2φ∈[0，1]∴t∈[32，52]【点评】：本题考查极坐标与直角坐标的互化，考查圆的参数方程的运用，属于中档题．。

大同一中、同煤一中2015届高三上学期期末联合考试文科数学试题第Ⅰ卷 客观卷（共60分）一、选择题：（每小题5分，共60分。

）1． 集合{|42}A x x =-≤≤，{|4}B y y x ==≤≤，则下列关系正确的是( ) A ．R R A B ⊆痧 B ．R A B ⊆ð C ．R B A ⊆ð D ．A B R =2． 若1z i =+，则z iz i +=( ) A ．2- B ．2i -C ．2D ．2i 3． 若命题:P x R ∀∈，211x +≥，则该命题的否定是（ ）A ．x R ∀∈，211x +≤B ．x R ∀∈，211x +<C ．x R ∃∈，211x +<D ．x R ∃∈，211x +≤ 4．若关于x 的方程||220x x a --+=有两个不相等的实数解，则实数a 的取值范围是( ) A ．(1,)-+∞ B ．[1,)-+∞ C ．(,1)-∞- D ．(,1]-∞-5．△ABC 的外接圆的圆心为O ，若OH OA OB OC =++，则H 是△ABC 的( )A ．外心B ．内心C ．重心D ．垂心6．x 、y 满足约束条件20220220x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩，若z y ax =-取得最大值的最优解不唯一，则实数a 的值为( )A ．12或1-B ．2或12C ．2或1D ．2或1-7．如图，M 是半径R 的圆周上一个定点，在圆周上等可能的任取一点N ，连接MN ，则弦MN 的长的概率是( )A ．15B ．14C ．13 D ．128． 已知抛物线22y px =的焦点F 与双曲线22179x y -=的右焦点重合，抛物线的准线与x 轴的交点为K ，点A在抛物线上，且|||AK AF ，则△AFK 的面积为A ．4B ．8C ．16D ．329． 棱长为2的正四面体的四个顶点都在同一个球面上，若过该球心的一个截面如图所示，则图中三角形(正四面体的截面)的面积是A ．3 BC．2 D ．12510．函数()2tan f x x x =-在(,)22ππ-上的图象大致为11．已知定义在R 上的函数()f x 是奇函数，且满足3()()2f x f x -=，(2)3f -=-，数列{}n a 满足11a =-，且21n n S a n n =⨯+，则56()()f a f a += A ．3- B ．2- C ．3 D ．212．已知椭圆22122:1x y C a b += (0a b >>)与双曲线222:14y C x -=有公共的焦点，2C 的一条渐近线与以1C 的长轴为直径的圆相交于A 、B 两点，若1C 恰好将线段AB 三等分，则A ．2132a =B ．213a =C ．212b =D ．22b = 第II 卷 主观卷（共60分）二、填空题 (每小题5分，共20分)x x x xy y y y13．已知3sin()35x π-=，则5cos()6x π-= ． 14．若两个正实数x 、y 满足211x y+=，并且222x y m m +>+恒成立，则实数m 的取值范 围是 ．15．已知椭圆22221x y a b+= (0a b >>)的一个焦点为F ， 若椭圆上存在一个P 点，满足以椭圆短轴为直径的圆与线段PF 相切于该线段的中点，则该椭圆的离心率为 ．16．一个四面体的三视图如右上图所示，则该四面体的四个面中最大的面的面积为 ．三、解答题17．(10分) 一个盒子里装有三张卡片，分别标记有数字1、2、3，这三张卡片除标记的数字外完全相同，随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a 、b 、c(1) 求“抽取的卡片上的数字满足a b c +=”的概率；(2) 求“抽取的卡片上的数字a 、b 、c 不完全相同”的概率．18．(12分)已知数列{}n a 的各项均为正数，前n 项和为n S ，且(1)2n n n a a S +=(*n N ∈) (1) 求 n a ；(2) 设12n n b S =，12n n T b b b =+++，求n T ．19．(12分) △ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ，且8a b c ++=(1) 若2a =，52b =，求cos C 的值； (2) 若22sin cos sin cos 2sin 22B A A B C +=，且△ABC 的面积9sin 2S C =， 求a 和b 的值．20．(12分)如图所示，三棱柱ABC —A 1B 1C 1中，CA CB =，1AB AA =，160BAA ∠=(1) 证明：1AB AC ⊥求三棱柱ABC —A 1B 1C 1的体积．21．(12分)已知椭圆22221x y a b += (0a b >>)0x y +=的距离为(1) 求椭圆的方程；(2) 过点(0,1)M -作直线l 交椭圆于A 、B 两点，交x 轴于N 点，且满足75NA NB =-，求直线l 的方程．22．(12分) 设函数()ln m f x x x=+ (m R ∈)， (1) 当m e =时，求()f x 的极小值；(2) 讨论函数()()3x g x f x '=-零点的个数； (3) 若对任意0b a >> ()()1f b f a b a -<-恒成立，求m 的取值范围．2015届高三联考数学(文)答案与评分标准三、解答题17．18．19．20．(1)略(2) 3 21．22．。

大同市口泉中学2014－2015学年高三上学期摸底考试（理科）本试卷分为第I 卷（选择题）和第II 卷（非选择题）两部分.满分150分.考试时间120分钟.第Ⅰ卷（选择题 共60分）1.集合{}|(1)(2)0A x x x =-+≤，B ={}0x x <，则A B =U （ ） A ．(,0]-∞ B ．(,1]-∞ C ．[1,2] D ．[1,)+∞2.已知数列{}n a 是公比为q 的等比数列，且134a a ⋅=，48a =，则1a q +的值为（ ） A ．3 B ．2 C ．3或2- D ．3或3-3.对于常数m 、n ，“0mn >”是“方程221mx ny +=的曲线是椭圆”的（ ）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件4．设b a ,是平面α内两条不同的直线，是平面α外的一条直线，则”“b l a l ⊥⊥,是”“α⊥l 的A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件5．已知数列{}n a 为等比数列，且5642a a a =⋅，设等差数列{}n b 的前n 项和为n S ，若552b a =，则9S =A ．36B ．32C ．24D ．226．函数)(cos sin 42sin )(3R x x x x x f ∈-=的最小正周期为 A ．8πB ．4π C ．2π D ．π 7．一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的 等腰直角三角形，则该几何体的外接球的表面积为 A ．12π B ．43π C ．3π D ．123π8.已知,(1)()(4)2,(1)2x a x f x ax x ⎧>⎪=⎨-+≤⎪⎩是R 上的单调递增函数，则实数a 的取值范围为 ( )A ．(1，＋∞)B ．[4,8)C ．(4,8)D ．(1,8)9.函数ax x f x++=)110lg()(是偶函数，xx bx g 24)(-=是奇函数，则=+b a （ ） A.1 B. 1- C. 21-D. 2110.已知球的直径SC=4，A ，B 是该球球面上的两点，AB=2．∠ASC=∠BSC=45°则棱锥S —ABC 的体积为ABCD11.已知圆()()221:231C x y -+-=,圆()()222:349C x y -+-=,,M N 分别是圆12,C C 上的动点,P 为x 轴上的动点,则PM PN +的最小值为（ ）A．4 B1- C．6-D12．已知二次函数c bx ax x f ++=2)(的导数0)0('),('>f x f ，且)(x f 的值域为),0[+∞，则)0(')1(f f 的最小值为 A ．3 B ．25 C ．2 D ．23 第Ⅱ卷 非选择题 （共90分）二、填空题（本题共4个小题，每小题5分，共20分. 把每小题答案填在答题纸的相应位置） 13、由曲线sin ,cos y x y x ==与直线0,2x x π==所围成的平面图形(图中的阴影部分)的面积是14、在等比数列{}n a 中，若,81510987=+++a a a a 8998-=⋅a a ，则=+++109871111a a a a 15. 若函数x x x f 3)(3+=对任意的0)()2(],2,2[<+--∈x f mx f m 恒成立，则∈x .16、设()sin2cos2f x a x b x ＝＋，其中,,0a b R ab ∈≠.若()6f x f π⎛⎫≤⎪⎝⎭对一切x R ∈恒成立，则 ① 11012f π⎛⎫= ⎪⎝⎭； ② 7125f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭；③ ()f x 既不是奇函数也不是偶函数； ④ ()f x 的单调递增区间是()2,63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦； ⑤ 存在经过点(),a b 的直线与函数()f x 的图象不相交．以上结论正确的是__________________（写出所有正确结论的编号）． 三、解答题（6个题， 共70分）17．(10分）在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且B A A b a sin 2cos 3sin ,=+≥． (1)求角C 的大小； (2)求a bc+的最大值．18.（12分）已知数列{}n a 的前n 项和为n S ,且*22()n n S a n N =-∈,数列{}n b 满足11b =,且点*1(,)()n n P b b n N +∈在直线2y x =+上. (1)求数列{}n a 、{}n b 的通项公式; (2)求数列{}n n a b ⋅的前n 项和n D ;19.（12分）如图在四棱锥P ABCD -中,底面ABCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD ，且AD PD PA 22==． (1)求证：面PAB ⊥平面PDC ； (2)求二面角B PD C --的余弦值．B20.（12分）如图已知抛物线2:2C y px =的焦点坐标为(1,0)F ，过F 的直线交抛物线C 于A B ,两点，直线AO BO ,分别与直线m ：2x =-相交于M N ,两点． (1)求抛物线C 的方程；(2)证明△ABO 与△MNO 的面积之比为定值．21.已知函数()e x f x =,点(,0)A a 为一定点,直线()x t t a =≠分别与函数()f x 的图象和x 轴交于点M ,N ,记AMN ∆的面积为()S t . （1）当0a =时,求函数()S t 的单调区间；（2）当2a >时, 若0[0,2]t ∃∈,使得0()e S t ≥, 求实数a 的取值范围.22. 已知函数()()0≠++=x b xax x f ，其中R b a ∈,. ⑴若曲线()x f y =在点()()2,2f P 处切线方程为13+=x y ,求函数()x f 的解析式； ⑵讨论函数()x f 的单调性；⑶若对于任意的⎥⎦⎤⎢⎣⎡∈2,21a ，不等式()10≤x f 在⎥⎦⎤⎢⎣⎡1,41上恒成立，求b 的取值范围.参考答案（理科）一、选择题：(每小题5分,共60分) 1 2 3 4 5 6 7 8 9 10 11 12 BDBCACCBDCAC二、填空题：(每小题5分,共20分)13． 2-22 14．-5/3 15．(-2,2/3) 16．三、解答题：(共70分) 17．(10分)解：（1）sin A ＋3cos A ＝2sin B 即2sin (A ＋ 3)＝2sin B ，则sin (A ＋3)＝sin B ．…3分因为0＜A ，B ＜，又a ≥b 进而A ≥B ，所以A ＋ 3＝－B ，故A ＋B ＝23，C ＝3． (6)分（2）由正弦定理及（1）得 a ＋b c ＝sin A ＋sin B sin C ＝23[sin A ＋sin (A ＋ 3)]＝3sin A ＋cos A ＝2sin (A ＋6)．…9分 当A ＝3时，a ＋b c取最大值2．18．(Ⅰ)当1=n ,21=a当2≥n 时,1122n n n n n a S S a a --=-=-∴ 12(2)n n a a n -=≥,∴{}n a 是等比数列,公比为2,首项12a = ∴2n n a = 又点*1(,)()n n P b b n N +∈在直线2y x =+上,∴ 12n n b b +=+, ∴{}n b 是等差数列,公差为2,首项11=b ,∴21n b n =- (Ⅱ)∴(21)2n n n a b n ⋅=-⨯∴1234112325272(23)2(21)2n n n D n n -=⨯+⨯+⨯+⨯+-⨯+-⨯L L ①23451212325272(23)2(21)2n n n D n n +=⨯+⨯+⨯+⨯+-⨯+-⨯L L ②①—②得123411222222222(21)2n n n D n +-=⨯+⨯+⨯+⨯+⨯--⨯L LzyxOFEDCBAP1114(12)22(21)22(32)612n n n n n -++-=+⨯--⨯=---1(23)26n n D n +=-+19．(12分)(1)解法一：因为面PAD ⊥面ABCD 平面PAD I 面ABCD AD =ABCD 为正方形，CD AD ⊥，CD ⊂平面ABCD所以CD ⊥平面PAD ∴CD PA ⊥ …………………………2分 又22PA PD AD ==，所以PAD ∆是等腰直角三角形， 且2PAD π∠=即PA PD ⊥CD PD D =I ，且CD 、PD ⊆面PDCPA ⊥面PDC又PA ⊆面PAB 面PAB ⊥面PDC …………………………6分 解法二：如图,取AD 的中点O , 连结OP ,OF . ∵PA PD =, ∴PO AD ⊥. ∵侧面PAD ⊥底面ABCD ,PAD ABCD AD ⋂=平面平面,∴PO ABCD ⊥平面,而,O F 分别为,AD BD 的中点,∴//OF AB , 又ABCD 是正方形,故OF AD ⊥. ∵22PA PD AD ==,∴PA PD ⊥,2a OP OA ==. 以O 为原点,向量OA →,OF →,OP →为,,x y z 轴建立空间直线坐标系,则有(,0,0)2a A ,(0,,0)2a F ,(,0,0)2a D -,(0,0,)2a P ,(,,0)2a B a ,(,,0)2aC a -. ∵E 为PC 的中点, ∴(,,)424a a aE - …………………………2分(1)∵(,0,)22a a PA =-u u u r ,CD →=(0,-a,0) ∴PA →CD →=(a2,0,- a 2)(0,-a,0)=0,∴PA CD ⊥u u u r u u u r,从而PA CD ⊥,又PA PD ⊥,PD CD D =I ,∴PA PDC ⊥平面,而PA PAB ⊂平面,∴平面PAB ⊥平面PDC ． …………………………6分(2)由(1)知平面PDC 的法向量为(,0,)22a aPA =-u u u r .设平面PBD 的法向量为(,,)n x y z =r .∵DP →=(a 2,0, a 2),BD →=(-a,-a,0)∴由0,0n DP n BD ⋅=⋅=r u u u r r u u u r 可得⎩⎪⎨⎪⎧a 2x+0y+a 2z=0-a x-a y+0z=0取1x =,则y=-1,z=-1,故n →=(1,-1,-1) …………………………10分∴6cos ,232n PAn PA n PAa ⋅<>===⨯r u u u rr u u u r r u u u r , 即二面角B PD C --的余弦值为6,……………………12分 20．(12分)解：（1）由焦点坐标为(1,0) 可知12p= 所以2=p ,所以抛物线C 的方程为x y 42= …5分（2）当直线垂直于x 轴时，ABO ∆与MNO ∆相似， 所以21()24ABOMNO OF S S ∆∆==, …7分当直线与x 轴不垂直时，设直线AB 方程为(1)y k x =-, 设)y 2,(M -M ，)y 2,(N -N ，),(11y x A ，),(22y x B ，解2(x 1),4,y k y x =-⎧⎨=⎩ 整理得2222(42)0k x k x k -++=， …9分 所以121=⋅x x , …10分121sin 121224sin 2ABO MNOAO BO AOBS x x AO BO S MO NO MO NO MON ∆∆⋅⋅⋅∠∴==⋅=⋅=⋅⋅⋅∠,综上14ABO MNO S S ∆∆= …12分21.解: (I) 因为1()||e 2t S t t a =-，其中t a ≠ …………2分 当0a =，1()||e 2t S t t =，其中0t ≠ 当0t >时，1()e 2t S t t =，1'()(1)e 2t S t t =+，所以'()0S t >，所以()S t 在(0,)+∞上递增， ……………4分当0t <时，1()e 2t S t t =-，1'()(1)e 2t S t t =-+，令1'()(1)e 02tS t t =-+>， 解得1t <-，所以()S t 在(,1)-∞-上递增令1'()(1)e 02tS t t =-+<， 解得1t >-，所以()S t 在(1,0)-上递减 ………7分综上，()S t 的单调递增区间为(0,)+∞，(,1)-∞-()S t 的单调递增区间为(1,0)- （II ）因为1()||e 2t S t t a =-，其中t a ≠ 当2a >，[0,2]t ∈时，1()()e 2tS t a t =-因为0[0,2]t ∃∈，使得0()e S t ≥，所以()S t 在[0,2]上的最大值一定大于等于e1'()[(1)]e 2t S t t a =---，令'()0S t =，得1t a =- …………………8分当12a -≥时，即3a ≥时1'()[(1)]e 02t S t t a =--->对(0,2)t ∈成立，()S t 单调递增所以当2t =时，()S t 取得最大值21(2)(2)e 2S a =-令21(2)e e 2a -≥ ，解得 22ea ≥+ ， 所以3a ≥ …………………10分 当12a -<时，即3a <时1'()[(1)]e 02t S t t a =--->对(0,1)t a ∈-成立，()S t 单调递增1'()[(1)]e 02t S t t a =---<对(1,2)t a ∈-成立，()S t 单调递减所以当1t a =-时，()S t 取得最大值11(1)e 2a S a --=令11(1)e e 2a S a --=≥ ，解得ln 22a ≥+所以ln 223a +≤< …………………12分22、解：⑴2()1af x x'=-，由导数的几何意义得(2)3f '=，于是8a =-． 由切点(2,(2))P f 在直线31y x =+上可得27b -+=，解得9b =． 所以函数()f x 的解析式为8()9f x x x=-+.............3分 ⑵2()1a f x x'=-． 当0a ≤时，显然()0f x '>(0x ≠),这时()f x 在(,0)-∞，(0,)+∞上内是增函数． 当0a >时，令()0f x '=，解得x = 当x 变化时，()f x '，()f x 的变化情况如下表：x(,-∞()+∞()f x ' ＋ 0 － － 0 ＋ ()f x↗极大值↘↘极小值↗∴()f x在(,-∞，)+∞内是增函数，在(，(0,)+∞内是减函数． (7)分⑶由⑵知，()f x 在1[,1]4上的最大值为1()4f 与(1)f 的较大者，对于任意的1[,2]2a ∈，不等式0(1)f x ≤在1[,1]4上恒成立，当且仅当10(11(4)10)f f ≤≤⎧⎪⎨⎪⎩，即39449a b ab ≤-≤-⎧⎪⎨⎪⎩，对任意的1[,2]2a ∈成立．从而得74b ≤，所以满足条件的b 的取值范围是(7,]4-∞．......12分。