教育科研中的统计方法——Z检验和t检验

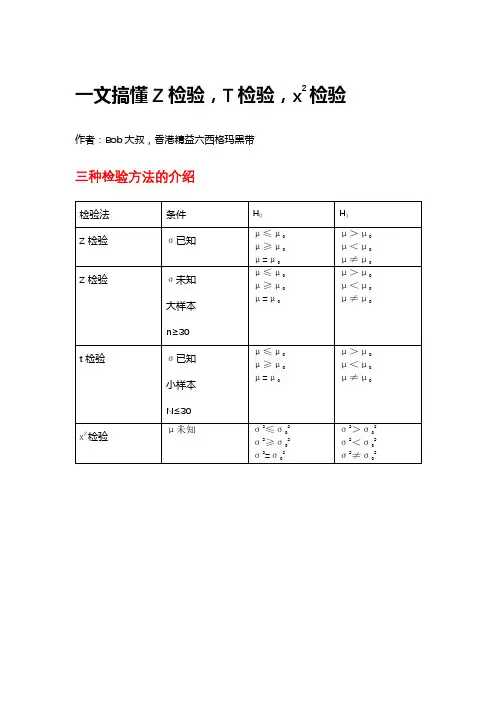
一文搞懂Z检验，T检验，x2检验作者：Bob大叔，香港精益六西格玛黑带
三种检验方法的介绍
Z检验举例：
某产品，其装量服从N（2.1，0.012），即均值2.1，标准差0.01。

抽取15个样品，其测量值如下：
2.08 2.10 2.10
2.09 2.10 2.10
2.09 2.09 2.11
2.09 2.12 2.10
2.10 2.10 2.10
建立假设H0:μ=2.1，H1 μ≠2.1，由于σ已知，故选择Z检验
操作如下：
P=0.36>0.05，无法拒绝原假设H0, 所以认为取样的平均装量没有变化。

t检验举例：
某设备的OEE目标为70%，连续15天的OEE如下，请判断OEE是否已达到70%目标？
由于σ（标准差）未知，且为小样本，故而选择，t检验
建立假设：HO: μ=70%, H1>70%,
操作如下：
P=0.252>0.05，无法拒绝原假设，说明0EE并未大于70%。

X2检验举例：
已知某产品装量，符合N（μ，σ2）分布，μ未知，但是要求标准差不能超过0.01，随机抽取30个样品，请问标准差是否有变化？
由于μ未知，故而选择X2检验，
建立假设：H0:σ=0.01, H1:σ≠0.01
操作如下：
（weixin gongzhonghao: HK_BobUncle）
P=0.303>0.05, 无法拒绝原假设，说明标准差无变化。

X
32.03 + 32.14 + … + 31.87 15
…
1.9 2.0
…
0.029 0.023
…
0.028 0.022
…
0.027 0.022
…
0.0226 0.020
…
0.025 0.020
…
0.024 0.019
…
0.024 0.019
…
0.023 0.018
原假设 （零假设）即上述的可能，符号是H0
备择假设（与原假设对立的假设），符号是H1
如本例：假设外径尺寸 H0：（μ = 32） H1： （μ≠32） 确立检验水准： α——显著水平（通常取α=0.05）

显著水平α是当原假设正确却被拒绝的概率 通常人们取0.05或0.01 这表明，当做出接受原假设的决定时，其正确的可 能性（概率）95% 或99% 概率是0～1之间的一个数，因此小概率就是接近0的 一个数 英国统计家Ronald Fisher 把0.05作为标准，从此0.05 或比0.05小的概率都被认为是小概率
8 作出不拒绝零假设的统计结论，即外径尺寸 均值没有偏离目标Ф 32
<6>
单样本 Z 检验 单样本 t 检验
预备知识
接上页

假设检验的例子（1）
检验 α = 0.05
临界值 临界值

2
=0.025
拒绝范围

1 – α = 95%
不拒绝H0范围
2
=0.025
根据小概率原理，可以先假设总体参数的 某项取值为真，也就是假设其发生的可能 性很大，然后抽取一个样本进行观察，如 果样本信息显示出现了与事先假设相反的 结果（显示出小概率），则说明原来假定 的小概率事件(一次实验中是几乎不可能发 生）在一次实验中居然真的发生了，这是 一个违背小概率原理的不合理现象，因此 有理由怀疑和拒绝原假设；否则不能拒绝 原假设。 在给定了显著水平α 后，根据容量为n的样 本，按照统计量的理论概率分布规律，可 以确定据以判断拒绝和接受原假设的检验 统计量的临界值。 临界值将统计量的所有可能取值区间分为 两个互不相交的部分，即原假设的拒绝域 和接受域。

药物治疗
1
？ ＝
药物治疗合 并饮食疗法
2
推断
甲组
n1=12
XX1 =15.21
乙组 n2=13 X 2=10.85
t 检验——问题提出
▪ 根据研究设计,t检验有三种形式：
➢单个样本的t检验 ➢配对样本均数t检验(非独立两样本均数t
检验)
➢两个独立样本均数t检验
第一节 单个样本t检验
▪ 又称单样本均数t检验(one sample t test),适 用于样本均数与已知总体均数μ0的比较,目的是 检验样本均数所代表的总体均数μ是否与已知总 体均数μ0有差别。
▪ 配对设计主要有三种情况：
（1）将受试对象按某些混杂因素（如性别、年龄、窝别 等）配成对子，每对中的两个个体随机分配给两种处理 （如处理组与对照组）； （2）同一受试对象或同一标本的两个部分，随机分别进 行不同处理（或测量）。 （3）同一受试对象自身前后对照。
配对t检验原理
▪ 配对设计的资料具有对子内数据一一对应的特征, 研究者应关心是对子的效应差值而不是各自的效 应值。
表 5-1 12 名儿童分别用两种结核菌素的皮肤浸润反应结果(mm)
编号
标准品 新制品 差值 d
d2
1
12.0
10.0
2.0
4.00
2
14.5
10.0
4.5
20.25
3
15.5
12.5
3.0
9.00
4
12.0
13.0
-1.0
1.00
5
13.0
10.0
3.0
9.00
6
12.0
5.5
6.5
42.25

z 检验/u 检验、t 检验、F 检验、卡方检验使用条件1. z 检验/u 检验（1）当样本容量30n >，即大样本时，样本相关系数r 就近似服从正态分布，经过对r 标准化变换后，则得到检验统计量：r r u σ= 或 σ=r rz 式中，r σ表示样本相关系数r 的抽样平均误差，即样本相关系数与总体相关系数之间的平均偏差。

（2）当在0ρ≠的总体中随机抽样时，样本相关系数r 并不呈正态分布，若要测定相关系数与0ρ≠的数值是否显著，或测定两个相关系数之间的差异是否显著，即从两个已知样本相关系数推断其总体相关系数是否相等的假设，费歇（Fisher ）在1921年提出了如下方法: 012:H ρρ= 112:H ρρ≠11ln 21r r z r +=- 经过对r 变化，则r z 就接近正态分布。

r z 的标准差为：()r z σ= 在简单直线方程式中只有两个参数，故2m =，则()r z σ=因此，此时可用正态分布方法进行检验。

The general form of a lower-tail test, whereis the stated value for the population mean, follows.Large-Sample (30≥n ) Hypothesis Test About a Population Mean for a One-Tailed Test of the Form00:μμ≥H 0:μμ<a HTest Statistic ：σ Assumed Knownn x z /0σμ-=Test Statistic ：σ Estimated by s0μn s x z /0μ-=Rejection RuleUsing test statistic ：Reject 0H if α<-z zUsing -p value ：Reject 0H if α<-value p2.t 检验当样本容量30n <，即小样本时，如果总体相关系数0ρ=，则样本相关系数r 的抽样分布随着样本容量n 的增大而逐渐地趋近于自由度为n m -的t 分布。

因为Ｚ = 6.97 > Ｚ 0.01, 所以P <0.01，
差异有统计学意义（P<0.01），
故拒绝H0，认为该地男、女间红细胞数
有显著差别，男高于女。
.
24
t 检验的应用条件
1、正态性 2、方差齐性
.
25

方差齐性检验
两独立样本均数比较的t 检验，
要求相应的两总体方差相等，即方 差具有齐性。为此，我们要对两样 本的方差作统计学检验
140
27
2
150
138
-12
3
150
140
-10
4
135
135
0
5
128
135
7
6
100
120
20
7
110
147
37
8
120
114
-6
9
130
138
8
10
123
120
-3
使用配对ｔ检验
解：１.建立检验假设，确定检验水准
Ｈ0：μd=0，假设该药不影响血红蛋白的变
化，即治疗前后总体差数为0。
Ｈ1：μd≠0 ，假设该药影响血红蛋白的变
.
21
1. H0 : μ1= μ2 ，即该地男、女红细胞数相
同,
Ｈ1 : μ1 ≠ μ2 ，该地男、女红细胞数不相
同。
α=0.05.
.
22
2. 计算Ｚ 值
Z
X1 X2
S
2 1
S
2 2
n1 n 2
4.654.22
6.97
(0.55)2 (0.44)2
156 104

t
X1 X2
( n1
1
)
S
2 1
(n2
1
)
S
2 2
(
1
1
)
n1பைடு நூலகம் n2 2
n1 n2
2.656 5.150
7.581
(9 1)0.475 2 (8 1)0.852 2 (1 1 )
982
98
n1 n2 2 1 5
3. 确定P值, 作出推断结论
查t界值表得, t0.05/2,15＝2.131, t0.01/2,15=2.947,
资料所提供的信息: 1. 计量资料 2. 配对设计。
表7.1 贫血患儿治疗一个疗程前后血红蛋白(g/L)变化情况
对上面问题可以作如下考虑：
治疗前后血红蛋白 的变化（差值）
d
问题归纳： 样本疗效
样本
n10 Sd7.96d137.53
d 0?
药物作用 + 机遇
d33.5
μ 0? d
问题：| d 究0 |竟多大能够下“有效”的结论？
对资料进行分析: 1. 资料提供的信息: 小样本计量资料
已知总体均数0=72次/分, n=25,
x74.2次/分S = 6.0次/分。 2. 应进行样本均数与已知总体均数比
较的t 检验。 3. 目的: 推断样本所代表的未知总体均
数与已知的总体均数有无差别。
(1) 建立检验假设，确定检验水准
H0：=0, 山区成年男子脉搏均数与一般成年
S/ n 6 25
0.01＜p＜0.05
例7.2 以往通过大规模调查已知某地新 生儿出生体重为3.30kg, 从该地难产儿中 随机抽取35名新生儿作为研究样本,平均 出生体重为3.42kg, 标准差为0.40kg。问 该地难产儿出生体重是否与一般新生儿体 重不同？

z检验和t检验的区别
卡方检验是对两个或两个以上样本率（构成比）进行差别比较的统计方法。

t检验，主要是用于小样本（样本容量小于30）的两个平均值差异程度的检验方法。

它是用t分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。

t检验的适用条件：正态分布资料。

1、卡方检验是用途非常广的一种假设检验方法，它在分类资料统计推断中的应用，
包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡仿检验以及分
类资料的相关分析等。

2、t检验，亦称student t检验( student's ttest) ，主要用作样本含量较小(比
如n大于30) ，总体标准差o未明的正态分布。

t检验就是用t原产理论去推断差异出现
的概率，从而比较两个平均数的差异与否明显。

t检验
3、t检验共分成三种方法，分别就是单一制样本t检验，接合样本t检验和单样本t
检验。

单一制样本t检验和单因素方差分析功能上基本一致，但是单一制样本t检验就可
以比较两组选项的差异，比如说男性和女性。

相对来讲，独立样本t检验在实验比较时使用频率更高，尤其是生物、医学相关领域。

针对问卷研究，如果比较的类别为两组，独立样本t检验和单因素方差分析均可实现，研
究者自行选择使用即可。

4、卡方分析：卡方检验用作分析定类数据与定类数据之间的关系情况。

比如研究人
员想要晓得两组学生对于手机品牌的偏好差异情况，则必须采用卡方分析。

卡方就是通过
分析相同类别数据的相对挑选频数和比重情况，进而展开差异推论，单选题或多选题均可
以采用卡方分析展开对照差异分析。

统计学检验方法比较统计学检验方法是在统计学中用来判断研究假设是否成立的一种方法。

它通过分析样本数据来推断总体参数，并根据结果得出判断。

在进行统计学检验之前，我们首先需要明确研究问题和研究假设。

接下来，我将介绍一些常见的统计学检验方法的比较。

1.T检验和Z检验T检验和Z检验都是用来推断一个样本的均值是否与总体均值有显著差异。

T检验主要用于小样本，而Z检验适用于大样本。

相较于Z检验，T检验考虑到了样本的自由度，因此对于小样本的推断更加准确。

2.单样本检验和双样本检验单样本检验用于比较一个样本的均值是否与一个已知的总体均值有显著差异。

双样本检验则用于比较两个样本的均值是否存在显著差异。

双样本检验可以进一步分为独立样本检验和配对样本检验。

独立样本检验适用于两个独立的样本，而配对样本检验适用于同一组个体在不同时间或不同处理下的两次测量。

3.卡方检验和F检验卡方检验主要用于判断两个分类变量之间是否存在相关性。

它将观察频数与期望频数进行比较，以确定差异的显著性。

F检验则用于比较两个或更多个总体方差是否相等。

它将组间离散度与组内离散度进行比较，从而推断总体方差是否存在显著差异。

4.非参数检验和参数检验非参数检验不依赖于总体的特定分布，而是对总体的分布进行较少的假设。

它通过对数据的排序和秩次转换来进行推断。

非参数检验一般适用于数据不服从正态分布或样本量较小的情况。

参数检验则建立在对总体参数分布的假设上，通常假设数据服从正态分布。

参数检验的推断结果相对较为准确，但对数据的假设要求较高。

综上所述，不同的统计学检验方法适用于不同的研究问题和数据类型。

选择合适的统计学检验方法可以提高推断结果的准确性。

因此，在进行统计学检验之前，我们需要充分理解研究问题的背景，研究假设的特点以及数据的类型和分布，从而选择适当的检验方法。

同时，还需要注意检验过程中的假设和限制，以及结果的解释和推断的合理性。

第四节 t 检验和u检验
t-test或称Student’s t-test; u-test或称Z-test
应用： 用于两均数比较的假设检验；
资料要求： （1）资料随机取自正态总体 （2）两总体方差齐性（相等）
除上述条件外，u检验还要求： 样本含量比较大（如n≥50）, 或n虽小但σ已知
（很少见）。 （t分布逼近u分布，或本身呈u分布）
注意：统计分析是 在H0前提下进行的
H0: = 0 （72次/分）
H1: > 0
单侧： = 0.05
t X 0
S/ n
74.2 72 1.833 6.0 / 25
=74.2
此图为从 0总体中抽样（n=25)得 到的样本均数分布图
＝ｎ－ 1＝25 －１＝24 查t界值表（P302），得单侧 t0.05，24 = 1.711 因: t =1.833> t0.05，24 所以：P < 0.05
方差齐 性检验
Equa l varian ces assum ed Equa l varian ces not assume d
Leve ne 's Te st fo r Equa lity of Variance s
F
S i g.
.015
.905
t-test for Equa lity of Mea ns
x
/ n
则 u 服从标准正态分布 N（0，1）
实际工作中， 往往未知，s 代替, 此时
就不是u代换，而是 t 代换。
t X X
Sx S/ n
无数t点所组成的分布，称t分布。
t 分布的特征： （1）以 0 为中心，两侧对称的单峰分布 （2）与 u 分布比较，峰值较低，两边上翘

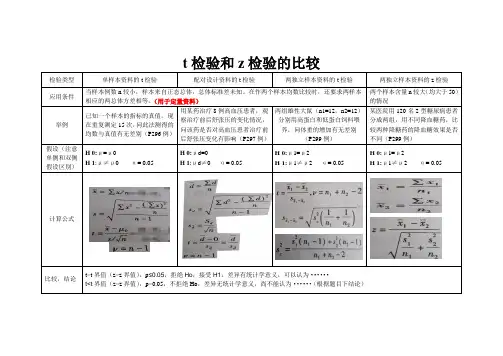
t检验和z检验的比较
检验类型单样本资料的t检验配对设计资料的t检验两独立样本资料的t检验两独立样本资料的z检验
应用条件当样本例数n较小，样本来自正态总体，总体标准差未知。

在作两个样本均数比较时，还要求两样本
相应的两总体方差相等。

（用于定量资料）
两个样本含量n较大（均大于50）
的情况
举例已知一个样本的指标的真值，现
在重复测定15次，问此法测得的
均数与真值有无差别（P296例）
用某药治疗8例高血压患者，观
察治疗前后舒张压的变化情况，
问该药是否对高血压患者治疗前
后舒张压变化有影响（P297例）
两组雄性大鼠（n1=12，n2=12）
分别用高蛋白和低蛋白饲料喂
养，问体重的增加有无差别
（P299例）
某医院用120名2型糖尿病患者
分成两组，用不同降血糖药，比
较两种降糖药的降血糖效果是否
不同（P299例）
假设（注意单侧和双侧假设区别）H 0:μ=μ0
H 1:μ≠μ0 α= 0.05
H 0:μd=0
H 1:μd≠0 α= 0.05
H 0:μ1=μ2
H 1:μ1≠μ2 α= 0.05
H 0:μ1=μ2
H 1:μ1≠μ2 α= 0.05
计算公式
比较，结论t>t界值（z>z界值），p≤0.05，拒绝Ho，接受H1，差异有统计学意义，可以认为······
t<t界值（z<z界值），p>0.05，不拒绝Ho，差异无统计学意义，尚不能认为······（根据题目下结论）。

４.统计分析不能代替专业分析。
假设检验结果“有”或“无”统计学意 义，主要说明抽样误差的可能性大小。在分 析资料时还必须结合临床医疗，预防医学特 点，来加以分析。例如，某两种药物降低血 压相差5毫米汞柱，经检验认为有统计学意义， 但这种差异在临床却没有什么意义。
总之，不能用统计分析来代替专业分析， 当然，也不能认为统计分析可有可无
因为Ｚ = 6.97 > Ｚ 0.01, 所以P <0.01，
差异有统计学意义（P<0.01），
故拒绝H0，认为该地男、女间红细胞数
有显著差别，男高于女。
t 检验的应用条件
1、正态性 2、方差齐性
方差齐性检验
两独立样本均数比较的t 检验，
要求相应的两总体方差相等，即方 差具有齐性。为此，我们要对两样 本的方差作统计学检验
同时降低α与β
b
七、使用ｔ 检验的注意事项
１.所观察的样本必须具备代表性，随 机性和可靠性;如果是两个样本比较，一 定要注意两个样本间的齐同均衡性，即 可比性。
２.必须根据实验设计的不同，选择不 同假设检验方法。
譬如，资料性质不同，设计类型不
同，样本大小不同，选用配对ｔ检验
还是两独立样本t检验，选用大样本还 是小样本检验，这些都涉及到最后进 行统计处理时使用不同公式。
练习：(1)某地测定30岁以上健康人与 冠心病病人的血清胆固醇结果见表3。 问：健康人与冠心病病人血清胆固醇量 有无不同（不必计算）？

表3 血清胆固醇资料

────────────────────────────

编号
健康人
冠心病病人
────────────────────────────

一、背景介绍统计学是一门研究数据收集、分析和解释的学科，统计检验方法是统计学的重要应用之一。

在统计学中，t值、z值和x2值是常见的统计指标，它们对应着不同的统计检验方法，用于检验样本数据是否符合特定的分布或者是否存在差异。

本文将对t检验、z检验和卡方检验进行详细介绍，分析它们的应用场景、计算方法和实际意义。

二、 t检验t检验是一种用于比较两个样本均值是否存在显著差异的统计方法。

当样本数据符合正态分布且方差未知时，可以采用t检验进行假设检验。

t检验分为单样本t检验和双样本t检验两种。

1. 单样本t检验单样本t检验用于检验样本均值是否等于已知的总体均值。

它的计算公式为：t = (样本均值 - 总体均值) / (标准误差)其中，标准误差的计算需要用到样本标准差和样本容量。

2. 双样本t检验双样本t检验用于比较两个独立样本的均值是否存在显著差异。

在双样本t检验中，需要计算t值和自由度，然后查找t分布表得出显著性水平。

如果t值大于临界值，则拒绝原假设，认为两组样本均值存在显著差异。

三、 z检验z检验是一种用于比较样本均值与总体均值差异的统计方法。

当样本容量较大且符合正态分布时，可以采用z检验进行假设检验。

z检验通常用于总体标准差已知且样本容量较大的情况。

z检验的计算公式为：z = (样本均值 - 总体均值) / (总体标准差 / 样本容量的平方根)根据z值查找标准正态分布表可以得出样本均值的显著性水平。

如果z 值落在临界值之外，则可以拒绝原假设，认为样本均值存在显著差异。

四、卡方检验卡方检验是一种用于检验观察频数与期望频数之间是否存在显著差异的统计方法。

在实际应用中，卡方检验通常用于分析分类数据的拟合度或者独立性。

1. 卡方拟合度检验卡方拟合度检验用于检验观察频数与期望频数之间的拟合度。

计算公式为：X2 = Σ((观察频数 - 期望频数)2 / 期望频数)根据卡方分布表可以得出显著性水平，从而判断观察频数是否符合期望频数的分布。

• 平均数之间进行比较要用t检验(大样本可用 Z检验)，率的比较要用 z 检验。进行检验 时，应根据不同的要求, 选用相应的计算公 式, 不能弄错。
T检验的适用条件
• t检验的应用条件和注意事项 • 两个小样本均数比较的t检验有以下应用条件： • （1）两样本来自的总体均符合正态分布， • （2）两样本来自的总体方差齐。 •
▲ 适用条件： （1）已知/可计算两个样本均数及它们的标准差 ； （2）两个样本之一的例数少于100； （3）样本来自正态或近似正态总体； （4）方差齐性
五、t检验注意事项
1. 要有严密的抽样设计 随机、均衡、可比
2. 选用的检验方法必须符合其适用条件 注意：t检验的前提是资料服从正态分布 3. 单侧检验和双侧检验
例 两法测定12份尿铅含量的结果
样品号
1 2 3 4 5 6 7 8 9 10 11 12 合计
尿铅含量（μmol.L－1）
简便法 常规法 差值（d ）
2.41
2.80
-0.39
2.90
3.04
-0.14
2.75
1.88
0.87
3.23
3.43
-0.20
3.67
3.81
-0.14
4.49
4.00
0.49
• 若是单组设计，必须给出一个标准值或者 总体均值，同时，提供一组定量的观测结 果，应用t检验的前提条件就是该组资料必 须服从正态分布；
• 若是配对设计，每对数据的差值必须服从 正态分布；
• 若是成组设计，个体之间相互独立，两组 资料均取自正态分布的总体，并满足方差 齐性。之所以需要这些前提条件，是因为 必须在这样的前提下所计算出的t统计量才 服从t分布。

统计检验的具体操作
①Z检验
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。

它是用标准正态分布的理论来推断差异发生的概率，从而比较两个独立大样本平均数的差异是否显著。

②t检验（计量）
t检验是用于小样本(样本容量小于30)时的平均值差异程度检验方法。

它是用t分布理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。

③χ2检验(计数)
Z检验与t检验，通常用于计量资料的分析，而在教育研究中还常有计数资料，如按品质分类，然后按类评等计数，如优良中差，甲乙丙丁，或同意、反对、弃权等。

这种计算资料检验就要利用χ2检验的方法。

χ是希腊字母，读chi ，通常把χ2读作“卡方”。

χ2检验是通过对所得的计数资料与依据某种假设而确定的理论次数二者之间的差异来进行检验的。

χ2值是检验实测次数与理论次数之间差异程度的指标。

两者相差越大，χ2值就越大；两者越接近，则χ2值就越小：如果两者完全相同，那么χ2值就等于零，χ2值永远是非负值。

χ 2值与P值及差异显著性的关系
χ 2（计算值）P 差异显著性
χ 2＞χ2（df）0.01P＜0.01 差异非常显著χ 2≥χ2（df）0.05 P≤0.05 差异显著
χ 2＜χ2（df）0.05P≥0.05 差异不显著4秩计算（0用分等级资料分析）。

X1
population
sample 2
X2
……
sample r
Xr
observation X：z X (3 13) sample mean X： z X
n
is unknown
mean X： t X ,
Sn
df n 1
X
~N
,
2
n
z-distribution versus t-distribution
Testing sample X should be a sample of a normal random variable. 检验样本是 来自正态总体的随机样本
If X is not normal, t will have an unknown distribution and, strictly speaking, the t-test is inapplicable. However, according to the central limit theorem, as the sample size increases, the distribution of t tends to be normal. Therefore, if the sample size is big, we can use the t-test even if X is not normal. But there is no way to find out what value is big enough. This value depends on how X deviates from the normal distribution. Some sources claim that n should be greater than 30, but sometimes even this size is not enough. Alternatively, we can use non-parametric test: Wilcoxon rank-sign test.〔见p79，第九章〕

语言教学研究常用统计方法一、为什么要用统计方法对数据进行分析如果不利用统计方法对数据进行分析，就不能从原始数据中得出可靠的结如果不使用统计方法进行分析，我们很难说两个班的成绩有显著差异。

二、几种常用的统计方法（一）T检验（T test）使用目的：比较两组数据的平均值是否有显著差异数据类型：数值数据注意事项：独立样本与配对样本；单侧检验与双侧检验例1：独立样本T检验：检验实验班与控制班的平均成绩是否有显著差异。

方法1：使用Excel中的TTEST方法2：使用SPSS中的Analyze→Compare means→Independent samples例2：配对样本T检验：检验实验前与实验后的成绩是否有显著差异。

方法1：使用Excel中的TTEST方法2：使用SPSS中的Analyze→Compare means→Paired samples T test（二）单方向方差检验（One-way Anova）使用目的：比较两组以上数据的平均值是否有显著差异，比如比较三个班的成绩。

数据类型：数值数据注意事项：1个自变量，1个因变量例3：单方向方差检验（One-way Anova）：检验三种教学的效果（成绩）是否有显著差异方法：使用SPSS中的Analyze→Compare means→One-way Anova（三）双方向方差检验（Two-way Anova）使用目的：比较两组以上数据的平均值是否有显著差异，并且需要考察两个变量之间的交互作用，比如调查地区与性别是否影响学生的成绩。

数据类型：数值数据注意事项：2自变量，1个因变量例4：双方向方差检验（Two-way Anova）：检验学生的性别和他们来自的地区是否相互作用影响学生的成绩。

方法：使用SPSS中的Analyze→General linear model→Univariate （1）依次点击SPSS中的Analyze→General linearmodel→Univariate（2）把因变量（成绩）放入DEPENDENT VARIABLE 方格中；把所有自变量放入FIXED FACTORS方格中；（3）点击OPTIONS，然后在ESTIMATED MARGINAL MEANS 中把所有的因素拖到DISPLAY MEANS FOR的方格中；（4）在DISPLAY区域选中DESCRIPTIVE STATISTICS和ESTIMATES OF EFFECT SIZE boxes；然后点击Contintue回到Univariate主窗口；（5）如何任何变量有3个或3个以上的情况，则需要点击POST-HOCS，把超过3种情况的变量拖入POST-HOCTESTS FOR方格。