符合导线严密平差(带公式)

附合导线方位角闭合差计算公式的探讨
附合导线方位角闭合差是实现控制周解导线法运算的一种重要参数。

它代表了解导线和要控制的对准方位角之间的实际差异。

其指标越小，控制效果越好，说明解导线和要控制的对准方位角实际越接近。

附合导线方位角闭合差可以通过下面的计算公式来确定：
附合导线方位角闭合差=[解导线末附密对准方位角-（起点对准方位角+中间导线折返总差）]xK
其中，K为参数，默认值为1. K的取值会影响控制效果，当K取值较大时，附合导线方位角闭合差将变大，说明控制效果较差；当K取值较小时，附合导线方位角闭合差将变小，说明控制效果较好。

以上是附合导线方位角闭合差计算公式的原理。

有了上述计算公式，我们可以得出控制效果的一个指标，从而方便我们对控制周解导线法运算的结果进行判断与比较。

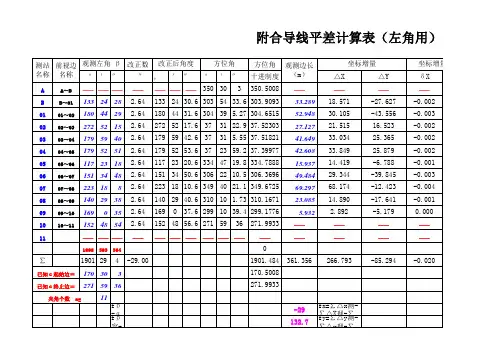
附合导线平差计算表（左角用）
计算：检查：
注意事项:
1、使用时，先根据实际点数的多少插入或删除行数。

但第五行和第六行不得删除，夹角个数行及上6行不要删除，目的是为了保
持公式的正确性，行数确定后，从第六行F列到W列选中，把公式拉到您需要的行数
2、“蓝色”字体表示计算时，需要输入的项目，根据实际数据情况进行填写。

3、要根据使用的等级导线，来修改“角度闭合差限差”计算公式(N20数据)及“导线全长相对闭合差”(Q22数据)
4、如果“N21”和“Q22”显示超限则数据不可用，要重新进行测量
5、计算好后可以把不需要显示的列隐藏起来，如“M”列
）。

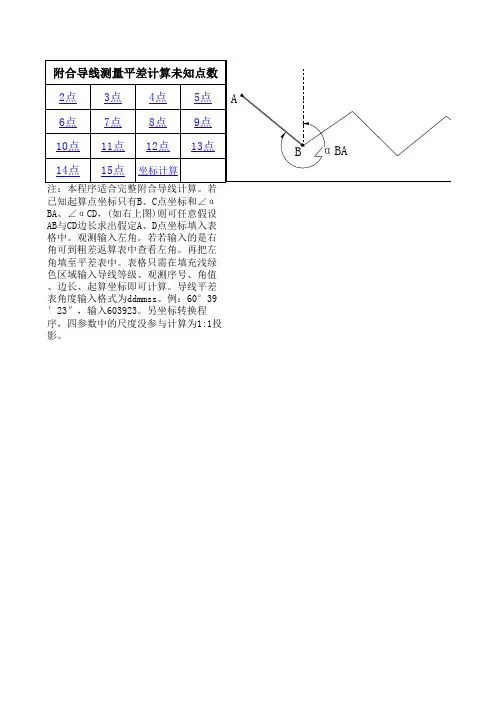
附合导线平差内业计算附合导线平差内业计算一、主要公式（左角）：如图：有： αB1=αA B +βB ±180°α12=αB1+β1±180° α23=α12+β2±180° α3C =α23+β3±180°αCD =α3C +βC ±180°计算终边坐标方位角的一般公式为：α终边′=α始边+Σβ测±n ×180°角度闭合差：ƒβ测=α终边′-α终边 ，ƒβ允=±10n （一级导线技术要求），式中n 为导线观测角个数。

如果ƒβ测>ƒβ允 ，则说明测角误差超限，应停止计算，重新检测角度。

如果ƒβ测>ƒβ允，说明测角精度符合要求，此时需要进行角度闭合差的调整。

调整是应注意:当用左角计算α终边′时，改正数的符号与ƒβ测符号相反；当用右角计算α终边′时，改正数的符号与ƒβ测符号相同。

可将闭合差按相反符号平均分配给各观测角，而得出改正角：V 改=-ƒβ测/n式中n 内角的个数，计算的改正数，取位至秒。

根据公式β＝β测+V改 得出改正后的观测角，继而算出新的方位角。

为了检核，最后应重新推算结束边的坐标方位角，它应与已知数值相等。

否则，应重新推算。

坐标增量闭合差：ΔX AB =D AB ×COS(αAB ),ΔY AB =D AB ×SIN(αAB ) ΔX B1=D B1×COS(αB1),ΔY B1=D B1×SIN(αB1) ΔX 12=D 12×COS(α12),ΔY 12=D 12×SIN(α12) ΔX 23=D 23×COS(α23),ΔY 23=D 23×SIN(α23) ΔX 3C =D 3C ×COS(α3C ),ΔY 3C =D 3C ×SIN(α3C )按附合导线的要求，各边坐标增量代数和的理论值ΣΔX i 、ΣΔY i ，应等于终、起两点的已知坐标值之差。

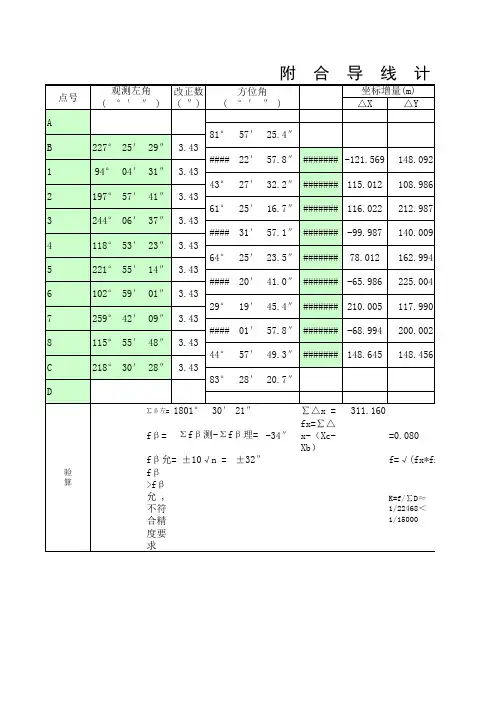
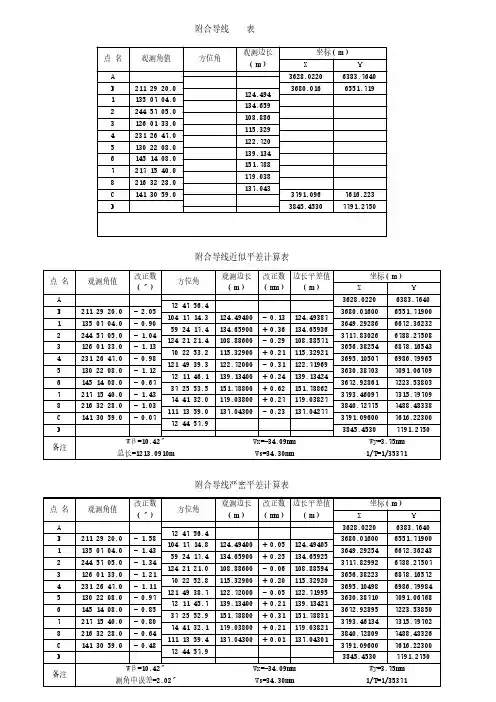
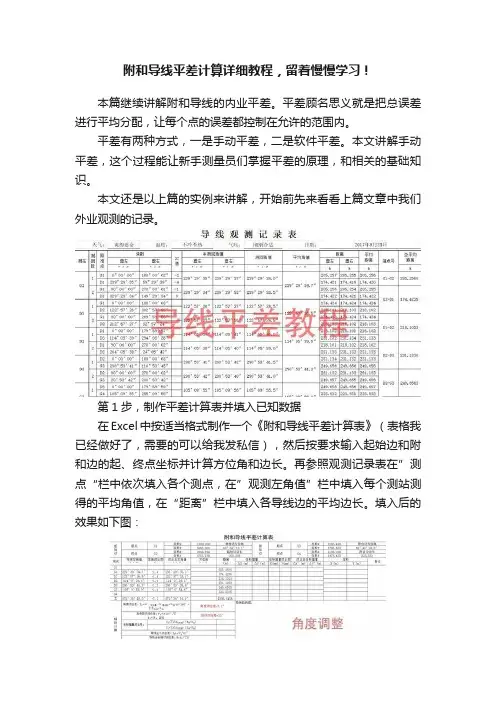
附和导线平差计算详细教程，留着慢慢学习！本篇继续讲解附和导线的内业平差。

平差顾名思义就是把总误差进行平均分配，让每个点的误差都控制在允许的范围内。

平差有两种方式，一是手动平差，二是软件平差。

本文讲解手动平差，这个过程能让新手测量员们掌握平差的原理，和相关的基础知识。

本文还是以上篇的实例来讲解，开始前先来看看上篇文章中我们外业观测的记录。

第1步，制作平差计算表并填入已知数据在Excel中按适当格式制作一个《附和导线平差计算表》（表格我已经做好了，需要的可以给我发私信），然后按要求输入起始边和附和边的起、终点坐标并计算方位角和边长。

再参照观测记录表在”测点“栏中依次填入各个测点，在”观测左角值”栏中填入每个测站测得的平均角值，在“距离”栏中填入各导线边的平均边长。

填入后的效果如下图：注：已知边的方位角和边长的计算方式很多，比如用5800计算器的Pol函数，道路之星的测站、CASS查询等。

第2步，计算角度闭合差计算角度闭合差，是为了检验外业角度观测的精度是否满足相应等级导线的技术要求。

如果实测的角度闭合差<>相关计算公式：实测角度闭合差=实测附和边方位角-理论附和边方位角实测附和边方位角=起始边方位角-N*180+实测左角值之和容许角度闭合差各等级导线有相应规定（各等级导线的技术要求在上篇文章中）。

注：N为测量站数，方位角取值范围是0度（含）到360度（不含），大于360度的减去360度，小于0度的加上360度。

本案例经计算：角度闭合差=7.1秒，容许闭合差=22秒，观测精度合格。

第3步，计算左角改正数经过角度闭合差的计算，确定外业成果合格后，就要计算左角改正数。

左角改正数=角度闭合差的相反数/测站个数改正后左角值=观测左角值+左角改正数本案例角度闭合差=7.1秒，那么左角改正数=-7.1/5=-1.42秒。

分配说明：为尽量平均分配误差，我们可将改正数保留1位小数，所以案例中每个测站分配-1.4秒，这时还有0.1秒未得到分配。

附合导线严密平差算法总结图1如图的单一附合导线，有4个已知点A、B、C、D，2个未知点TP1、TP2。

设观测边数为n, 则未知点数为n-1, 观测角数为n+1。

以上图为例，n = 3。

观测边为：S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路：由于A、B坐标已知，则可以算出起始方位角，再根据B点坐标和每个观测角（夹角，左角）推算出TP1、TP2、C点的近似坐标值。

如果是用全站仪进行测量，则用盘左盘右重复观测求平均的方式，直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。

再根据c点的已知坐标与近似坐标求坐标闭合差，由CD的已知方位角和近似方位角求角度闭合差，两个闭合差联立求得边长和角度的改正数，最后求得未知点的坐标平差值。

条件平差过程：1.建立条件方程，求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下：1、建立条件方程在单一附合导线中，只需要三个条件方程即：方位角附合条件、纵坐标附合条件和横坐标附合条件方程。

（省略了条件方程的推导过程，详细过程请查看参考资料：《测量平差.pps》）（1）方位角附合条件[Vβi]n+11+ Wβ= 0式中，Wβ= - （T0– T CD+ [βi]n+11 - （n+1）*180°）（角度闭合差）βi ——角度观测值（夹角，左角）Vβi ——各观测角的改正数。

如果是用全站仪观测，则Wβ= - （T CD– T CD）式中，T CD ——CD的方位角观测值，T CD ——CD的已知方位角（2）纵坐标X附合条件方程[Cos TI * VSi]1n - （1/ ρ”）* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值（近似值）Yi——待定点的横坐标Y的观测值Wx = - （Xn+1- XC）XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65（3）横坐标Y附合条件方程[Sin TI * VSi]1n + （1/ ρ”）* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值（近似值）Xi——待定点的纵坐标X的观测值WX = - （Yn+1- YC）YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组：[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为：（即改正数V的系数，此处以图1为例， n = 3）3、联系数法方程（简称法方程）AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N：N = AP-1A T（权的推导见参考资料：《全站仪观测导线测量平差方法的研究.pdf》）角度权：P βi = 1；（因为角度的标称精度是固定的，各观测角权值相等） 边长权：P Si = (μ0 *μ0 ) / （M D * M D ）（误差比例系数固定，边长的误差与距离有关，因此不一致）式中，μ0 ——先验测角中误差，以秒为单位 M D —— 距离观测中误差若 导线边长为S i （米），e1 为仪器的边长标称固定误差（mm ），e2为仪器的边长比例误差系数（无单位），则M D = ± （e1 + e2 * S i * 0.001）mm 需转化为厘米：M D = M D ** 0.1 （cm ）由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数（P 是对角矩阵，对角矩阵的逆矩阵就是原矩阵元素的倒数） Psi = 1/ Psi ；由上可得，P -1 矩阵如下：4、求改正数由于N 已经在前面的步骤中求出，求N 的逆矩阵。

附合导线按条件平差算例9.4.1附合导线的条件平差方程式如图9-6所示，符合在已知),(A A y x A ，),(C C y x C 之间的单一符合导线有n 条AB α与CDα是已知方位角。

设观测角为β、β、… …、β，测角中误差为 ，观测边长为s 、s 、… …、s ，故t1为v 1=ii BACD 011=+∑+=a i n i v ω （9-2）式中a ω—方位角条件的不符值，按180)1(ˆ11+-∑+-=+=n in i CD BAaβααω （9-3）若导线的A 点与C 点重合，则形成一闭合导线，由此坐标方位角条件就成了多边形的图形闭合条件。

2、纵、横坐标条件 设以1ˆx ∆、2ˆx ∆、…、n x ˆ∆表示图中各导线边的纵坐标增量之平差值；1ˆy∆、2y ∆、…、n yˆ∆表示图中各导线边的横坐标增量之平差值；由图可写出以坐标增量平差值表示的纵、横坐标条件。

⎪⎪⎭⎪⎪⎬⎫∑+∆∑+=∆∑+=∑+∆∑+=∆∑+=∆∆yi n i n A i n A C xi n i n A i nA C v y y yy y v x x xx x 111111ˆˆ （9-4）σ令⎪⎪⎭⎪⎪⎬⎫--∆∑=--∆∑=)()(11A Ci nyA C i nx y y y x x x ωω （9-5）则⎪⎪⎭⎪⎪⎬⎫=+∑=+∑∆∆0011yyi nx xi nv v ωω （9-6） 以微分量代替改正数，则有)()()(211n xi nx d x d x d v ∆++∆+∆=∑∆{}ρα1231211)()()(cos v y y y y y y v v n Csi i nxin-'++-+--∑=∑∆将上式代入式9-6得纵坐标条件式，且同理已可得横坐标的条件式即⎪⎪⎭⎪⎪⎬⎫=+-'∑+∑=+-'∑-∑====0)(1sin 0)(1cos 1111y i i Cni sii n i x i i Cni si i n i v x x v v y y v ωραωρα （9-7）上式就是单一符合导线的纵、横坐标条件方程x ω、y ω为条件式的不符值，按⎪⎪⎭⎪⎪⎬⎫-'=-∆∑+=-'=-∆∑+=C CCi nA yC CC i nA x y y y y y x x x x x 11ωω （9-8）式中i x 、i y 是由观测值计算的各导线点的近似坐标。

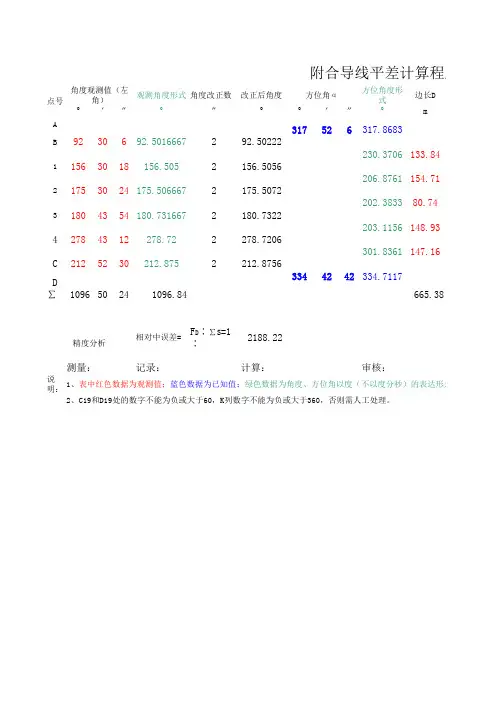
观测角度形式角度改正数改正后角度方位角度形式边长D°′″°″°°′″°m A D∑109650241096.84665.38相对中误差=F D ∶∑S =1∶2188.22说明：1、表中红色数据为观测值；蓝色数据为已知值；绿色数据为角度、方位角以度（不以度分秒）的表达形式，会自动计2、C19和D19处的数字不能为负或大于60，K列数字不能为负或大于360，否则需人工处理。

测量：记录：计算：审核：4C 27843122125230B 1292175156方位角α180.7322230.3706206.8761202.3833203.115631804354角度观测值（左角）点号31752630243063018180.731667222292.5016667156.505175.506667精度分析附合导线平差计算程序278.72212.87522278.7206212.8756175.507292.50222156.50563344242317.8683133.84154.7180.74148.93301.8361334.7117147.16ΔxΔyυxυyΔx′Δy′xy-357.369-387.255-0.13071-0.27455秒）的表达形式，会自动计算，可隐藏；紫色数据为平差结果。

-137.00277.59672日期：-125.021-0.02926-0.02891-58.5294-125.082-0.06145-0.060723802.8514006.77-70.00253903.6333805.1083833.6313943.138-103.137-30.77924028.533730.436坐标增量计算值(m)坐标增量改正数（m)改正后的坐标增量（m)坐标(m)-0.05522-0.06384-0.03331-0.02629-0.03039-85.3658程序-0.01586-85.3921-138.03-74.6727-103.082-69.9386-30.7459-137.999-74.6568-136.9733671.033619.243593.4333744.32277.62563-58.468。