算法报告-旅行商问题模板讲解

关于旅行商问题的数学模型旅行商问题（TravelingSalesmanProblem，TSP）是著名的组合优化问题，它的目标是找到一条路径，使得一个旅行商可以经过所有给定的城市，路径总长度最短。

这个问题在实际生活中有着广泛的应用，例如物流配送、电路板布线、DNA序列比对等领域。

本文将介绍旅行商问题的数学模型和解法。

1. 问题描述假设有n个城市，它们的位置分别为(xi,yi)，i=1,2,...,n。

旅行商要从一个城市出发，经过所有城市恰好一次，最后回到出发城市。

城市之间的距离可以用欧几里得距离表示：d(i,j) = sqrt((xi-xj)^2 + (yi-yj)^2)旅行商问题的目标是找到一条路径，使得路径总长度最短。

2. 数学模型2.1 定义变量我们定义变量xij表示从城市i到城市j的路径是否被选择，如果被选择则xij=1，否则xij=0。

例如，x12表示从城市1到城市2的路径是否被选择。

2.2 目标函数旅行商问题的目标是找到一条路径，使得路径总长度最短。

因此，我们可以定义目标函数为：minimize ∑i∑j d(i,j)xij其中，i,j表示城市的编号，d(i,j)表示城市i和城市j之间的距离，xij表示从城市i到城市j的路径是否被选择。

2.3 约束条件旅行商需要经过所有城市恰好一次，因此我们需要添加以下约束条件：1. 每个城市只能被经过一次：∑j xij = 1, i=1,2,...,n2. 每个城市离开后只能到达一个城市：∑i xij = 1, j=1,2,...,n3. 不能出现子回路：∑i∈S ∑j∈S xij ≤ |S|-1, S{1,2,...,n}, |S|≥2其中，第一个约束条件表示每个城市只能被经过一次，第二个约束条件表示每个城市离开后只能到达一个城市，第三个约束条件表示不能出现子回路。

3. 解法旅行商问题是一个NP难问题，没有多项式时间算法可以求解。

因此，我们需要使用一些启发式算法来求解这个问题。

图算法--旅⾏商问题旅⾏商问题的描述试想⼀下，⼀个业务员因⼯作需要必须访问多个城市。

他的⽬标是每个城市只访问⼀次，并且尽可能地缩短旅⾏的距离，最终返回到他开始旅⾏的地点，这就是旅⾏商问题的主要思想。

在⼀幅图中，访问每个顶点⼀次，并最终返回起始顶点，这个访问的轨迹称为哈密顿圈。

要解决旅⾏商问题，需要⽤图G=（V，E）作为模型，寻找图中最短的哈密顿圈。

G是⼀个完整的、⽆⽅向的带权图，其中V代表将要访问的顶点的集合，E为连接这些顶点的边的集合。

E中每条边的权值由顶点之间的距离决定。

由于G中⼀个完整的、⽆⽅向的图，因此E包含V（V-1）/2条边。

事实上，旅⾏商问题是⼀种特殊的⾮多项式时间问题，称为NP完全问题。

NP完全问题是指那些多项式时间算法未知，倘没有证据证明没有解决的可能性的问题。

考虑到这种思想，通常⽤⼀种近似算法来解决旅⾏商问题。

最近邻点法的应⽤⼀种近似的计算旅⾏商路线的⽅法就是使⽤最近邻点法。

其运算过程如下：从⼀条仅包含起始顶点的路线开始，将此顶点涂⿊。

其他顶点为⽩⾊，在将其他顶点加⼊此路线中后，再将相应顶点涂⿊。

接着，对于每个不在路线中的顶点v，要为最后加⼊路线的顶点u与v之间的边计算权值。

在旅⾏商问题中，u与v之间边的权值就是u到v 之间的距离。

这个距离可以⽤每个顶点的坐标计算得到。

两个点（x1，y1）与（x2，y2）之间距离的计算公式如下：r = √（x2 - x1）2 + （y2 - y1）2 （注意是求和的平⽅根）利⽤这个公式，选择最接近u的顶点，将其涂⿊，同时将其加⼊路线中。

接着重复这个过程，直到所有的顶点都涂成⿊⾊。

此时再将起始顶点加⼊路线中，从⽽形成⼀个完整的回路。

下图展⽰了使⽤最近邻点法来解决旅⾏商问题的⽅法。

通常，在为旅⾏商问题构造⼀个图时，每个顶点之间相连的边不会显⽰表⽰出来，因为这种表⽰会让图不清晰了，也没有必要。

在图中，每个顶点旁边都显⽰其坐标值，虚线表⽰在此阶段需要⽐较距离的边。

91、实验题目人工智能实验报告——旅行商问题旅行商问题：从某个城市出发，每个城市只允许访问一次，最后又回到原来的城市， 寻找一条最短距离的路径。

请定义两个h 函数（非零），讨论这两个函数是否都在h*的下界范围，是否满足单调限制？你认为哪个会产生比较有效的搜索？2、实验目的及要求旅行商问题是图论中的一个重要的经典问题，本次实验要求学生要求自行定义两个h 函数（非零），独立编写程序解决旅行者问题，语言不限，工具不限，独立完成实验报告。

通过本次实验，使学生加深对图搜索策略的理解和认识，对启发式搜索、估价函数有更深入的理解认识，并学会灵活掌握及解决实际问题。

3、实验设备装有Office 软件的微机一台，本次实验使用Visual studio 6.0开发环境4、实验内容本实验首先对旅行商问题进行了学习了解，之后结合人工智能课堂内容，设计了两个h 函数，使用C 语言编写实现。

具体说明及步骤如下。

4.1、旅行商问题旅行商问题是图论中的一个重要的经典问题: 任给一个城市与城市间的道路图, 求一个旅行商访问每个城市并回到出发点的最短路程。

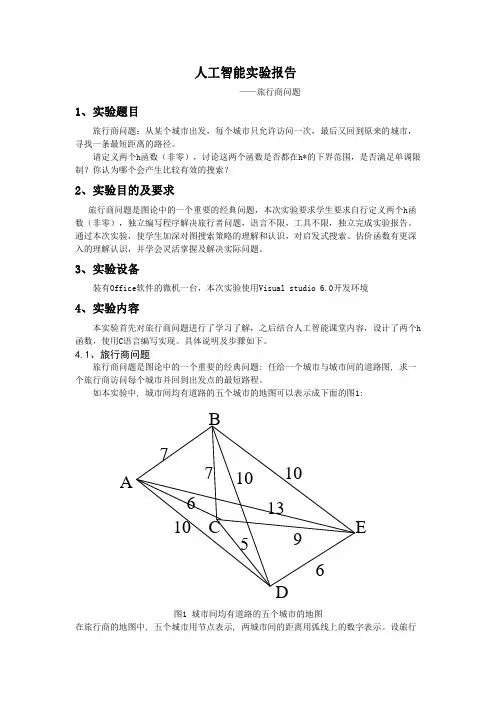
如本实验中, 城市间均有道路的五个城市的地图可以表示成下面的图1:B7 A7 10 10 6 13 10 CE56D图1 城市间均有道路的五个城市的地图在旅行商的地图中, 五个城市用节点表示, 两城市间的距离用弧线上的数字表示。

设旅行商从A 城市出发, 到B、C、D、E 等城市去推销商品, 要寻找一条从A 出发, 包括B、C、D、E, 且仅包含一次, 最后回到A 的一条最短路径。

4.2、A*算法A* 算法是N.Nillson于1971年提出的一种有序搜索算法, 该算法被认为是求解人工智能问题的最成功的技术理论之一。

Nillson指出对于某一已到达的现行状态, 如已到达图中的n节点, 它是否可能成为最佳路径上的一点的估价, 应由估价函数f(n)值来决定。

假设g*(n)函数值表示从起始节点s 到任意一个节点n 的一条最佳路径上的实际耗散值。

基于优化算法的求解旅行商问题大一时我第一次学习了旅行商问题，当时我感到很惊讶：这个看起来非常简单的问题，却有着很难解决的复杂性。

只有问题规模足够小的时候，我们才能用穷举法来解决。

对于问题规模稍大一些的情况，我们便需要采用一种优化算法。

近年来，一些优秀的优化算法的出现，使得旅行商问题高效求解成为了可能。

标准的旅行商问题描述如下：给定一系列城市和每对城市间的距离，求解访问每一座城市一次并回到起始城市所需要的最短路线，即访问n个城市的所有路径的最小值。

这个问题的解法其实很直观：我们可以按照某种固定的顺序，计算每一种可能路径的长度，最后选取其中最短的。

然而，这种方法的难点在于计算出所有可能的路线很复杂，仅当问题规模很小的时候我们才可以用它来解决。

旅行商问题是一个非常重要的优化问题，它被广泛应用于物流、旅游等领域。

随着数据量的急剧增长，传统的优化算法效率越来越低。

这个时候，人们开始使用一些基于机器学习的优化算法。

其中，遗传算法和模拟退火算法备受瞩目。

遗传算法是一种基于生物学的演化理论的优化方法。

在遗传算法中，一个问题解的集合称为“种群”。

种群中的每个解称为“个体”，而且每个个体通过某种与适应度相关联的函数来评估质量。

适应度高的个体有更大的机会参与下一代种群的遗传操作。

在种群中，通过交叉、变异和选择等步骤实现演化。

选出种群中最好的个体，然后在该个体附近进行微小变化，这些变化可以是交换两个城市，也可以是插入某个城市。

这个过程类似于热力学中的模拟退火。

在这个过程中，我们允许一些不是最优的解被接受，以避免陷入局部最小值。

这个过程会逐渐降低温度，直到问题的解趋近于最优解。

在接下来的时间里，我将会解释这些算法的具体实现，并给出一些实验结果。

一、旅行商问题所谓旅行商问题(Travelling Salesman Problem , TSP)，即最短路径问题，就是在给定的起始点S到终止点T的通路集合中，寻求距离最小的通路，这样的通路成为S点到T点的最短路径。

在寻找最短路径问题上，有时不仅要知道两个指定顶点间的最短路径，还需要知道某个顶点到其他任意顶点间的最短路径。

遗传算法方法的本质是处理复杂问题的一种鲁棒性强的启发性随机搜索算法，用遗传算法解决这类问题，没有太多的约束条件和有关解的限制，因而可以很快地求出任意两点间的最短路径以及一批次短路径。

假设平面上有n个点代表n个城市的位置, 寻找一条最短的闭合路径, 使得可以遍历每一个城市恰好一次。

这就是旅行商问题。

旅行商的路线可以看作是对n 个城市所设计的一个环形, 或者是对一列n个城市的排列。

由于对n个城市所有可能的遍历数目可达(n- 1)!个, 因此解决这个问题需要0(n!)的计算时间。

假设每个城市和其他任一城市之间都以欧氏距离直接相连。

也就是说, 城市间距可以满足三角不等式, 也就意味着任何两座城市之间的直接距离都小于两城市之间的间接距离。

二、遗传算法1 遗传算法介绍遗传算法是由美国J.Holland教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的，它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。

通过模拟自然选择和自然遗传过程中发生的繁殖、交叉和基因突变现象，在每次迭代中都保留一组候选解，并按某种指标从解群中选取较优的个体，利用遗传算子(选择、交叉和变异)对这些个体进行组合，产生新一代的候选解群，重复此过程，直到满足某种收敛指标为止。

遗传算法在本质上是一种不依赖具体问题的直接搜索方法，是一种求解问题的高效并行全局搜索方法。

其假设常描述为二进制位串，位串的含义依赖于具体应用。

搜索合适的假设从若干初始假设的群体集合开始。

当前种群成员通过模仿生物进化的方式来产生下一代群体，如随机变异和交叉。

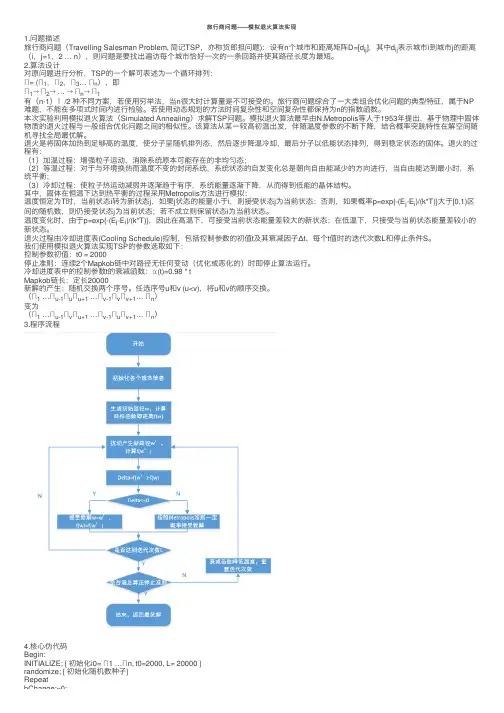
旅⾏商问题——模拟退⽕算法实现1.问题描述旅⾏商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D=[d ij]，其中d ij表⽰城市i到城市j的距离（i，j=1，2 … n），则问题是要找出遍访每个城市恰好⼀次的⼀条回路并使其路径长度为最短。

2.算法设计对原问题进⾏分析，TSP的⼀个解可表述为⼀个循环排列：Π= (Π1，Π2，Π3… Πn），即Π1→Π2→ … →Πn→Π1有（n-1）！/2 种不同⽅案，若使⽤穷举法，当n很⼤时计算量是不可接受的。

旅⾏商问题综合了⼀⼤类组合优化问题的典型特征，属于NP 难题，不能在多项式时间内进⾏检验。

若使⽤动态规划的⽅法时间复杂性和空间复杂性都保持为n的指数函数。

本次实验利⽤模拟退⽕算法（Simulated Annealing）求解TSP问题。

模拟退⽕算法最早由N.Metropolis等⼈于1953年提出，基于物理中固体物质的退⽕过程与⼀般组合优化问题之间的相似性。

该算法从某⼀较⾼初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间随机寻找全局最优解。

退⽕是将固体加热到⾜够⾼的温度，使分⼦呈随机排列态，然后逐步降温冷却，最后分⼦以低能状态排列，得到稳定状态的固体。

退⽕的过程有：（1）加温过程：增强粒⼦运动，消除系统原本可能存在的⾮均匀态；（2）等温过程：对于与环境换热⽽温度不变的封闭系统，系统状态的⾃发变化总是朝向⾃由能减少的⽅向进⾏，当⾃由能达到最⼩时，系统平衡；（3）冷却过程：使粒⼦热运动减弱并逐渐趋于有序，系统能量逐渐下降，从⽽得到低能的晶体结构。

其中，固体在恒温下达到热平衡的过程采⽤Metropolis⽅法进⾏模拟：温度恒定为T时，当前状态i转为新状态j，如果j状态的能量⼩于i，则接受状态j为当前状态；否则，如果概率p=exp{-(E j-E i)/(k*T)}⼤于[0,1)区间的随机数，则仍接受状态j为当前状态；若不成⽴则保留状态i为当前状态。

旅行商问题实验报告学院：计算机科学与技术专业：计算机科学与技术学号：班级：姓名：（本程序在ＭｉｃｒｏｓｏｆｔＶｉｓｕａｌＣ＋＋６．０的环境下实现）一、问题描述：某售货员要到若干城市去推销商品，已知各城市之间的路程（或旅费）。

他要选定一条从驻地出发，经过每个城市一遍，最后回到驻地的路线，使总的路程（或旅费）最小。

例如：给定4个城市{a，b，c，d}及其各城市之间的路程,找出其最短路径二、算法思想：首先是在图为完全图的前提下，构造各城市间的图的结构，采用邻接数组的形式，将各个城市间的距离存储于图的数组中，用一个函数递归寻找从同一个顶点出发的各个城市的所有路径，再求出各个路径的路程，并与相应的路径输出，对路程数组进行冒泡排序后，经比较找出最短路径并输出。

三．具体实现及分析：图结构的定义：struct MGraph{char vexs[MAX_VEX_NUM];//顶点向量int arcs[MAX_VEX_NUM][MAX_VEX_NUM];//邻接矩阵int vexnum,arcnum;//顶点数，边数};// AdjMatrix函数int CreateUDG(MGraph &G) 用数组邻接矩阵表示法构造无向图函数void Perm(Type list[], int k, int m)用于递归生成路径排列，并寻找最佳路径采用递归实现路径排列是一种比较简便的方法，但其需做(n-1)!/2次循环，时间复杂度为O((n-1)!/2),有待改进。

辅助数组Help[ ]对Count[ ]数组进行排序，找出最小值，当旅行商的地点大于等于5时，只比较Count[ ]数组的前半部分会有遗漏。

函数void Swap ( Type &a ,Type & b)用于递归时的字符交换函数函数void Inicialize(MGraph &G)//用于初始化各个数组，并调用递归函数Perm();主函数：void main()//主函数{int choice;//选择操作变量while(true){cout<<"请选择操作：1: 执行程序！0: 退出程序！"<<endl;cin>>choice;if (choice==1){CreateUDG(G);//函数调用Inicialize(G);cout<<endl;cout<<endl;}if (choice==0)break;}}三．源程序：#include<iostream>using namespace std;#define MAX_VEX_NUM 20//最大顶点数int **Mat;//定义动态二维数组，存储生成的排列int *list;//定义动态辅助数组int *Count;//定义动态计数数组int *Help;//定义动态辅助数组int e=0;//定义全局变量struct MGraph{char vexs[MAX_VEX_NUM];//顶点向量int arcs[MAX_VEX_NUM][MAX_VEX_NUM];//邻接矩阵int vexnum,arcnum;//顶点数，边数};// AdjMatrixMGraph G; //声明一个无向图的邻接矩阵类型int visited[MAX_VEX_NUM];//设置标志数组int Locatevex(MGraph G,char v)//图的基本操作，寻找顶点V的位置{int i=0;while(i<G.vexnum && v!=G.vexs[i])i++;if(i<G.vexnum)return i;//查找成功则返回顶点的下标elsereturn -1;}int CreateUDG(MGraph &G) //数组邻接矩阵表示法构造无向图{char v1,v2;int weight;//权值cout<<"请输入图的顶点数和弧数"<<endl;cin>>G.vexnum>>G.arcnum;cout<<"请输入顶点值"<<endl;for(int i=0;i<G.vexnum;i++)//构造顶点向量cin>>G.vexs[i];for(int q=0;q<G.vexnum;q++){for(int p=0;p<G.vexnum;p++){G.arcs[q][p]=0;//初始化邻接矩阵}}for(int k=0;k<G.arcnum;k++)//构造邻接矩阵{cout<<"输入该弧依附的顶点和权值："<<endl;cin>>v1>>v2>>weight;int a=Locatevex(G,v1);int b=Locatevex(G,v2);G.arcs[a][b]=weight;G.arcs[b][a]=G.arcs[a][b];}cout<<"图的顶点：";for(int n=0;n<G.vexnum;n++)//输出顶点cout<<G.vexs[n]<<" ";cout<<endl;cout<<endl;cout<<"该图的邻接矩阵表示为：\n";for(int x=0;x<G.vexnum;x++){for(int y=0;y<G.vexnum;y++){cout<<G.arcs[x][y]<<" ";//输出邻接矩阵}cout<<endl;}cout<<endl;cout<<endl;return 1;}//CreateUDGtemplate <class Type>void Perm(Type list[], int k, int m)//递归函数，生成排列，寻找最佳路径{int c=1;int a=m;while(a>1)//定义Mat数组的行数{c=c*a*(a-1);a-=2;}int d=m+1;//定义Mat数组的列数if ( k == m && list[0]==0){for(int i = 0; i <= m; i++){Mat[e][i]=list[i];//符合条件时生成排列，存储在数组Mat中}e++;}if(Mat[c-1][m]!=-1 && e==c )//当找出所有可能路径时，计算所有路径长度，并找到最短路径{for(int g=0;g<c;g++){for(int h=0;h<d;h++){int x=Mat[g][h];//获取路径坐标int y=Mat[g][h+1];Count[g]=Count[g]+G.arcs[x][y];//计算路径长度}}cout<<"所有路径及其路径长度："<<endl;for(g=0 ;g<c;g++)//输出所有路径及其路径长度{for(int h=0;h<=d;h++){int k=Mat[g][h];cout<<G.vexs[k]<<"->";}cout<<" "<<Count[g]<<endl;}for(g=0;g<c;g++)Help[g]=Count[g];//赋值for(int i=0;i<c;i++)//对辅助数组冒泡排序，找最小值{for(int j=1;j<c;j++){if (Help[i]>Help[j]){int temp=Help[i];Help[i]=Help[j];Help[j]=temp;}}}int Min_way=Help[0];//Min_way为最短路径for (i=0;i<c;i++){if (Count[i]==Min_way){cout<<"旅行商最佳路径为：";for(int j=0;j<=d;j++){int k=Mat[i][j];cout<<G.vexs[k]<<"->";//输出最短路径}cout<<" 路径长度为："<<Min_way;cout<<endl;}}}else{for ( int i = k; i <= m; i ++)//递归生成排列组合{Swap( list[k],list[i] );Perm(list,k + 1, m ) ;Swap( list[k], list[i] );}}}template < class Type >inline void Swap ( Type &a ,Type & b)//字符交换函数{Type temp = a; a = b; b = temp;}void Inicialize(MGraph &G)//初始化各个数组函数{int a=G.vexnum ;//图的顶点数，列数int b=a-1;//辅助变量int c=a-1;int n=1;//辅助变量,行数while(b>1){n=n*b*(b-1);b-=2;}Mat=new int*[n];for(int i=0;i<n;i++){Mat[i]=new int[a];for(int j=0;j<=a;j++){if (j<a){Mat[i][j]=-1;//数组初始化}else{Mat[i][j]=0;}}}list=new int[a];for(i=0;i<a;i++)//数组初始化list[i]=i;Count=new int[n];for(i=0;i<n;i++)Count[i]=0;//数组初始化Help=new int[n];for(i=0;i<n;i++)Help[i]=0;//数组初始化Perm(list,1,c);//函数调用}void main()//主函数{CreateUDG(G);//函数调用Inicialize(G);}四．运行结果：<1> 当顶点为4时：<2> 测试当顶点为5时：。

Astar算法求解旅行商问题一、问题描述一共有n个城市，某推销员从其中的一个城市A出发经过每个城市一次且仅一次后回到A，求代价最小的路径。

二、知识表示1、状态表示初始状态，目标状态。

初始状态：A（出发城市）目标状态：A，···（（n-1）个城市），A2、算法描述（1）设城市结点的个数为n，获取开始结点，计算所有成员变量的值，将开始结点放入open表（open表用队列实现）；（2）如果open表不为空，转（3），否则转（7）；（3）将open表中的首元素放入close表，并将该首元素从open表中删除。

（4）获取已访问结点的个数num，如果num ≥n+1，则找到最佳路径，转（7）；（5）如果num==n，还访问一个结点到达目标结点，设置初始结点的访问状态isVisited[0]的值为false，表示初始结点没有被访问，即可以回到出发点；（6）如果num<n，将从当前结点出发可访问的结点和open表中剩余的结点放入一个向量vector中，根据每个结点的fvalue值按升序排列，排列的结果按升序放入open表，转（2）；（7）获取close表中的最后一个元素，打印最佳路径，相邻城市之间的距离，最短的距离值。

3、估价函数f(n)=g(n)+h(n) ，h(n)≤h*(n)。

g(n)：从开始结点到当前结点n的实际距离，等于路径的权值的和。

h(n)：假设城市结点n的深度为depth，城市的个数为city_num，(city_num-depth)表示从n到目标城市还需要的路径个数，min表示所有路径长度的最小值，则h(n)=min*(city_num-deep)表示从当前城市结点n到目标结点的路径长度的最小估计值，h(n)≤h*(n)显然对于任意的一个城市结点都成立。

三、算法实现主要的数据结构城市结点：depth表是从开始城市到当前城市，访问的城市个数，也可以称为深度；num 表示已访问的城市结点的个数；id_list是一个数组，表示从开始城市到当前城市的所有城市的编号的集合，编号的值从1开始；isVisited是一个布尔数组，记录当前城市结点到目标城市结点的访问状态，布尔值为false，表示可访问；fvalue表示从开始城市出发回到原点的估计值。