c++动态规划试题+分析

动态规划算法详解及经典例题⼀、基本概念（1）⼀种使⽤多阶段决策过程最优的通⽤⽅法。

（2）动态规划过程是：每次决策依赖于当前状态，⼜随即引起状态的转移。

⼀个决策序列就是在变化的状态中产⽣出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

假设问题是由交叠的⼦问题所构成，我们就能够⽤动态规划技术来解决它。

⼀般来说，这种⼦问题出⾃对给定问题求解的递推关系中，这个递推关系包括了同样问题的更⼩⼦问题的解。

动态规划法建议，与其对交叠⼦问题⼀次重新的求解，不如把每⼀个较⼩⼦问题仅仅求解⼀次并把结果记录在表中（动态规划也是空间换时间的）。

这样就能够从表中得到原始问题的解。

（3）动态规划经常常使⽤于解决最优化问题，这些问题多表现为多阶段决策。

关于多阶段决策：在实际中，⼈们经常遇到这样⼀类决策问题，即因为过程的特殊性，能够将决策的全过程根据时间或空间划分若⼲个联系的阶段。

⽽在各阶段中。

⼈们都须要作出⽅案的选择。

我们称之为决策。

⽽且当⼀个阶段的决策之后，经常影响到下⼀个阶段的决策，从⽽影响整个过程的活动。

这样，各个阶段所确定的决策就构成⼀个决策序列，常称之为策略。

因为各个阶段可供选择的决策往往不⽌⼀个。

因⽽就可能有很多决策以供选择，这些可供选择的策略构成⼀个集合，我们称之为同意策略集合（简称策略集合）。

每⼀个策略都对应地确定⼀种活动的效果。

我们假定这个效果能够⽤数量来衡量。

因为不同的策略经常导致不同的效果，因此，怎样在同意策略集合中选择⼀个策略，使其在预定的标准下达到最好的效果。

经常是⼈们所关⼼的问题。

我们称这种策略为最优策略，这类问题就称为多阶段决策问题。

（4）多阶段决策问题举例：机器负荷分配问题某种机器能够在⾼低两种不同的负荷下进⾏⽣产。

在⾼负荷下⽣产时。

产品的年产量g和投⼊⽣产的机器数量x的关系为g=g(x)，这时的年完善率为a，即假设年初完善机器数为x，到年终时完善的机器数为a*x(0<a<1)；在低负荷下⽣产时，产品的年产量h和投⼊⽣产的机器数量y 的关系为h=h(y)。

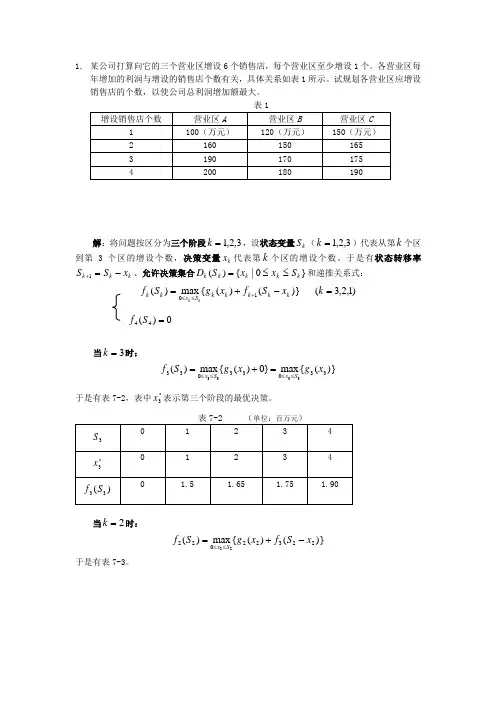
1． 某公司打算向它的三个营业区增设6个销售店，每个营业区至少增设1个。

各营业区每年增加的利润与增设的销售店个数有关，具体关系如表1所示。

试规划各营业区应增设销售店的个数，以使公司总利润增加额最大。

表1解：将问题按区分为三个阶段3,2,1=k ，设状态变量k S （3,2,1=k ）代表从第k 个区到第3个区的增设个数，决策变量k x 代表第k 个区的增设个数。

于是有状态转移率k k k x S S -=+1、允许决策集合}0|{)(k k k k k S x x S D ≤≤=和递推关系式：)}()({max )(10k k k k k S x k k x S f x g S f kk -+=+≤≤ )1,2,3(=k0)(44=S f当3=k 时：)}({max }0)({max )(330330333333x g x g S f S x S x ≤≤≤≤=+=于是有表7-2，表中*3x 表示第三个阶段的最优决策。

单位：百万元当2=k 时：)}()({max )(2232202222x S f x g S f S x -+=≤≤于是有表7-3。

表7-3 （单位：百万元）当1=k 时：)}()({max )(1121101111x S f x g S f S x -+=≤≤于是有表7-4。

故最优分配方案为：A 区建3个销售店，B 区建2个销售店，C 区建1个销售店， 总利润为490万元。

2． 某工厂有100台机器，拟分4个周期使用，在每一周期有两种生产任务，据经验把机器投入第一种生产任务，则在一个周期中将有六分之一的机器报废，投入第二种生产任务，则有十分之一的机器报废。

如果投入第一种生产任务每台机器可收益1万元，投入第二种生产任务每台机器可收益0.5万元。

问怎样分配机器在4个周期内的使用才能使总收益最大？ 解：阶段：将每个周期作为一个阶段，即k=1,2,3，4 状态变量：第k 阶段的状态变量k S 代表第k 个周期初拥有的完好机器数决策变量：决策变量k x 为第k 周期分配与第一种任务的机器数量，于是k k x S -该周期分配在第二种任务的机器数量。

长郡中学NOIP动态规划试题01试题名称程序名输入文件输出文件时限空间字串的距离blast. cpp blast.in blast.out 1s 128M 尼克的任务lignja. cpp lignja.in lignja.out 1s 128M1s 128M 数字金字塔numtri.cpp numtri.in numtri.out1s 128M 方格取数 fgqs .cpp fgqs.in fgqs.out1s 128M 多米诺骨牌 dom.cpp dom.in dom.out字符串的距离【问题描述】设有字符串X，我们称在X的头尾及中间插入任意多个空格后构成的新字符串为X的扩展串，如字符串X为“abcbcd”，则字符串“abcb□cd”，“□a□bcbcd□”和“abcb□cd□”都是X的扩展串，这里“□”代表空格字符。

如果A1是字符串A的扩展串，B1是字符串B的扩展串，A1与B1具有相同的长度，那么我们定义字符串A1与B1的距离为相应位置上的字符的距离总和，而两个非空格字符的距离定义为它们的ASCII码的差的绝对值，而空格字符与其它任意字符之间的距离为已知的定值K，空格字符与空格字符的距离为O。

在字符串A、B的所有扩展串中，必定存在两个等长的扩展串A1、B1，使得A1与B1之间的距离达到最小，我们将这一距离定义为字符串A、B的距离。

请你写一个程序，求出字符串A、B的距离。

【输入】输入第一行为字符串A，第二行为字符串B，A、B均由小写字母组成且长度均不超过2000，第三行为一个整数K，1≤K≤100，表示空格与其它字符的距离。

【输出】输出仅一行包含一个整数，表示要求的字符串A、B的距离。

【样例】blast.incmcsnmn2blast.out10尼克的任务【问题描述】尼克每天上班之前都连接上英特网，接收他的上司发来的邮件，这些邮件包含了尼克主管的部门当天要完成的全部任务，每个任务由一个开始时刻与一个持续时间构成。

以下是C++中的一些经典题目及其算法解析：1. 两数之和（Two Sum）题目描述：给定一个整数数组nums 和一个目标值target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

算法解析：可以使用哈希表来解决这个问题。

遍历数组，对于每个元素，计算目标和并减去当前元素，得到差值。

在哈希表中查找差值，如果存在则返回下标，否则将当前元素和下标存入哈希表。

2. 三数之和（3Sum）题目描述：给定一个包含n 个整数的数组nums，判断nums 中是否存在三个元素a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

算法解析：可以使用分治法来解决这个问题。

将数组分成A、B、C 三部分，分别求和并记录下标。

对于每个 A 的下标，分别判断 B 和 C 的部分是否存在和为-A 的数对，如果存在则返回结果。

3. 最长回文子串（Longest Palindromic Substring）题目描述：给定一个字符串s，找到s 中最长的回文子串。

你可以假设s 的最大长度为1000。

算法解析：可以使用动态规划来解决这个问题。

定义dp[i][j] 表示s[i..j] 是否为回文串。

根据回文串的性质，如果s[i] = s[j]，那么dp[i][j] 一定等于dp[i+1][j-1]。

因此，可以从字符串两端向中间遍历，每次判断两端字符是否相等，如果相等则更新dp 数组，最终找到最长的回文子串。

4. 二分查找（Binary Search）题目描述：给定一个有序数组nums 和一个目标值target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

算法解析：可以使用二分查找来解决这个问题。

定义left 和right 指针指向数组的左右两端，每次比较中间元素和目标值的大小关系，根据比较结果更新左右指针的位置，直到找到目标值或者左右指针相遇。

如果找到了目标值，还需要判断左右指针指向的元素是否相同。

C语⾔动态规划之背包问题详解01背包问题给定n种物品，和⼀个容量为C的背包，物品i的重量是w[i],其价值为v[i]。

问如何选择装⼊背包的物品，使得装⼊背包中的总价值最⼤？（⾯对每个武平，只能有选择拿取或者不拿两种选择，不能选择装⼊某物品的⼀部分，也不能装⼊物品多次）声明⼀个数组f[n][c]的⼆维数组，f[i][j]表⽰在⾯对第i件物品，且背包容量为j时所能获得的最⼤价值。

根据题⽬要求进⾏打表查找相关的边界和规律根据打表列写相关的状态转移⽅程⽤程序实现状态转移⽅程真题演练：⼀个旅⾏者有⼀个最多能装M公⽄的背包，现在有n件物品，它们的重量分别是W1、W2、W3、W4、…、Wn。

它们的价值分别是C1、C3、C2、…、Cn,求旅⾏者能获得最⼤价值。

输⼊描述：第⼀⾏：两个整数，M（背包容量，M<= 200)和N（物品数量，N<=30);第2…N+1⾏：每⾏两个整数Wi，Ci，表⽰每个物品的质量与价值。

输出描述：仅⼀⾏，⼀个数，表⽰最⼤总价值样例：输⼊：10 42 13 34 57 9输出：12解题步骤定义⼀个数组dp[i][j]表⽰容量为j时，拿第i个物品时所能获取的最⼤价值。

按照题⽬要求进⾏打表，列出对应的dp表。

W[i]（质量）V[i]（价值）01234567891000000000000210011111111133001334444444500135568899790013556991012对于⼀个动态规划问题设置下标时最好从0开始，因为动态规划经常会和上⼀个状态有关系！从上⾯的dp表可以看出来对于⼀个物品我们拿还是不难需要进⾏两步来判断。

第⼀步：判断背包当前的容量j是否⼤于物品当前的质量，如果物品的质量⼤于背包的容量那么就舍弃。

第⼆步：如果背包可以装下这个物品，就需要判断装下该物品获取的最⼤价值是不是⼤于不装下这个物品所获取的最⼤价值，如果⼤于那么就把东西装下！根据这样的思想我们可以得到状态转移⽅程：如果单签背包的容量可以装下物品:dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);如果当前背包的容量装不下该物品:dp[i][j]=dp[i-1][j];#include <stdio.h>int max(const int a,const int b){return a>b ? a:b;}int main(){int w[35]={0},v[35]={0},dp[35][210]={0};int n,m;scanf("%d %d",&m,&n);int i,j;for(i=1;i<=n;i++){scanf("%d %d",&w[i],&v[i]);}for(i=1;i<=n;i++){for(j=1;j<=m;j++){if(j>=w[i])//如果当前背包的容量⼤于商品的质量{dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);//判断是否应该拿下}else//⼤于背包的当前容量{dp[i][j]=dp[i-1][j];}}}for(int k=0;k<=n;k++){for(int l=0;l<=m;l++){printf("%d ",dp[k][l]);}printf("\n");}printf("%d\n",dp[n][m]);}通过运⾏以上程序可以看到最终的输出dp表和我们的预期是相符合的！但是并没有结束，动态规划有⼀个后⽆效性原则(当前状态只与前⼀个状态有关)。

2023深圳杯c题解析一、题目背景介绍2023年深圳杯竞赛C题旨在考察选手对于动态规划问题的理解和应用能力。

本题背景设定为一家公司，公司员工可以互相借用物品，但每次借用需要支付一定的费用。

题目要求我们计算公司员工借用物品的总费用，以便为公司提供更合理的收费策略。

二、题目要求分析1.数据范围：员工数量不超过500，物品数量不超过1000，借用费用不超过10000。

2.输入格式：第一行为一个整数n，表示员工数量。

接下来一行包含n个整数，表示每位员工借用的物品数量。

最后一行为n个整数，表示每次借用的费用。

3.输出格式：输出公司员工借用物品的总费用。

三、解题思路与方法本题可以使用动态规划求解。

我们可以设立一个dp数组，其中dp[i]表示前i个员工借用物品的总费用。

状态转移方程为：dp[i] = dp[i-1] + max(0, borrow[i] - borrow[i-1]) * cost[i]。

四、代码实现与注释```pythondef main():n = int(input())borrow = list(map(int, input().split()))cost = list(map(int, input().split()))dp = [0] * (n + 1)for i in range(1, n + 1):dp[i] = dp[i - 1] + max(0, borrow[i] - borrow[i - 1]) * cost[i - 1]print(dp[n])if __name__ == "__main__":main()```五、拓展与优化1.优化空间复杂度：只用一个dp数组即可求解，无需额外存储。

第1篇第一部分：基础知识1. C语言基础- 请简述C语言的特点和优势。

- 解释变量声明和初始化的区别。

- 描述C语言中的数据类型，包括基本类型和构造类型。

- 解释C语言中的运算符及其优先级。

- 描述C语言中的控制结构，包括if语句、循环语句（for、while、do-while）等。

2. 指针与数组- 解释指针的概念及其在C语言中的作用。

- 比较指针和数组的区别。

- 编写一个函数，使用指针交换两个整数的值。

- 描述如何使用指针遍历二维数组。

3. 函数与递归- 解释函数的定义和调用。

- 描述函数参数的传递方式，包括值传递和引用传递。

- 编写一个递归函数，计算斐波那契数列的第n项。

- 解释递归函数的优缺点。

4. 结构体与联合体- 解释结构体和联合体的概念。

- 描述结构体和联合体的区别。

- 编写一个结构体，包含姓名、年龄和性别等信息，并创建一个结构体数组。

5. 文件操作- 描述C语言中文件操作的基本概念。

- 编写代码，使用fopen、fprintf、fclose等函数实现文件的读取和写入。

第二部分：高级特性1. 动态内存分配- 解释动态内存分配的概念。

- 描述malloc、calloc、realloc和free函数的使用。

- 编写代码，动态分配内存，创建一个链表并插入元素。

2. 指针与函数- 解释函数指针的概念。

- 编写一个函数指针作为参数的函数。

- 描述如何使用函数指针来调用函数。

3. 宏定义与内联函数- 解释宏定义的概念及其优缺点。

- 编写宏定义，实现简单的数学运算。

- 描述内联函数的概念及其应用场景。

4. 编译预处理- 解释编译预处理的概念。

- 描述宏、条件编译、文件包含等预处理指令的使用。

5. C语言标准库- 描述C语言标准库中的常用函数，如printf、scanf、strlen等。

- 编写代码，使用标准库函数实现字符串复制、字符串连接等操作。

第三部分：编程实践1. 编写一个函数，计算一个整数数组中所有元素的和。