第一单元分数乘法复习

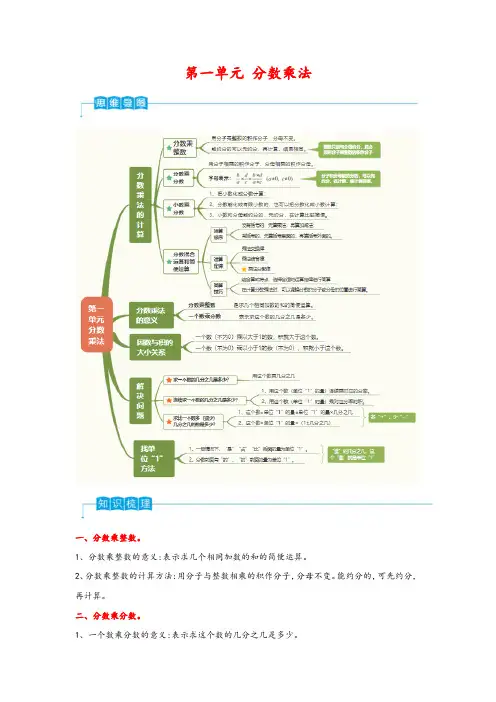
第一单元分数乘法
一、分数乘整数。

1、分数乘整数的意义:表示求几个相同加数的和的简便运算。

2、分数乘整数的计算方法:用分子与整数相乘的积作分子，分母不变。

能约分的，可先约分，再计算。

二、分数乘分数。

1、一个数乘分数的意义:表示求这个数的几分之几是多少。

2、分数乘分数的计算方法:用分子乘分子的积作分子，用分母乘分母的积作分母。

三、小数乘分数。

1、小数乘分数的计算方法。

(1)把小数化成分数计算；
(2)如果所乘分数能化成有限小数，也可以把分数化成小数计算；
(3)小数和分母能约分的，先约分，再计算比较简便。

四、分数混合运算和简便运算。

1、分数混合运算的运算顺序与整数混合运算的运算顺序相同。

算式里有括号的，要先算括号里面的；算式里没有括号的，要先算乘法，后算加、减法。

2、整数乘法的运算定律(交换律、结合律和分配律)对于分数乘法也同样适用。

五、解决问题。

1、连续求一个数的几分之几是多少的解题方法:用这个数(单位“1”的量)×几分之几×几分之几=部分量
2、求比一个数多(或少)几分之几的数是多少的解题方法。

(1)单位“1”的量×[1±几分之几]=这个数量；
(2)单位“1”的量±单位“1”的量×几分之几=这个数量。

一、选择题
15232534
二、填空题
三、判断题
四、计算题
21．（2023春·河南开封·六年级校考期中）看图列式计算。

五、解答题
参考答案1．C。

人教版数学六年级（上册）知识点梳理附复习要点各知识点梳理归纳（四）分数乘法混合运算1、分数乘法混合运算顺序与整数相同，先乘、除后加、减，有括号的先算括号里面的，再算括号外面的。

2、整数乘法运算定律对分数乘法同样适用；运算定律可以使一些计算简便。

乘法交换律：a×b＝b×a乘法结合律：(a×b)×c＝a×(b×c)乘法分配律：a×(b±c)＝a×b±a×c（五）倒数的意义：乘积为1的两个数互为倒数。

1、倒数是两个数的关系，它们互相依存，不能单独存在。

单独一个数不能称为倒数。

（必须说清谁是谁的倒数）2、判断两个数是否互为倒数的唯一标准是：两数相乘的积是否为“1”。

例如：a×b＝1，则a、b互为倒数。

3、求倒数的方法：①求分数的倒数：交换分子、分母的位置。

②求整数的倒数：整数分之1。

③求带分数的倒数：先化成假分数，再求倒数。

④求小数的倒数：先化成分数再求倒数。

4、1的倒数是它本身，因为1×1=1。

0没有倒数，因为任何数乘0积都是0，且0不能作分母。

5、真分数的倒数是假分数，真分数的倒数大于1，也大于它本身。

假分数的倒数小于或等于1。

带分数的倒数小于1。

（六）分数乘法应用题——用分数乘法解决问题1、求一个数的几分之几是多少？（用乘法）已知单位“1”的量，求单位“1”的量的几分之几是多少，用单位“1”的量与分数相乘。

2、巧找单位“1”的量：在含有分数（分率）的语句中，分率前面的量就是单位“1”对应的量，或者“占”“是”“比”字后面的量是单位“1”。

3、什么是速度？速度是单位时间内行驶的路程。

速度=路程÷时间（1）用比的前项和后项同时除以它们的最大公约数。

（2）两个分数的比，用前项后项同时乘分母的最小公倍数，再按化简整数比的方法来化简。

也可以求出比值再写成比的形式。

（3）两个小数的比，向右移动小数点的位置，也是先化成整数比。

六年级上册数学复习提纲第一单元 分数乘法1、分数乘法的意义：（1）分数乘整数：表示几个相同加数的和是多少；或表示一个数的几倍是多少。

如453⨯表示4个53相加是多少；或表示53的4倍是多少。

（2）一个数乘分数：表示一个数的几分之几（或几倍）是多少。

如6512⨯表示求12的65是多少。

41312⨯表示求12的413倍是多少。

2、分数乘法的计算方法：用分子相乘的积作分子，分母相乘的积作分母，能约分的先约分再计算。

3、整数乘法的交换律、结合律和分配律，对于分数乘法也适用，特别要注意乘法分配律的三种情况： 一是合并式，如：95)6165(61959565⨯+=⨯+⨯ 二是分散式，如：27274279827)27498(⨯+⨯=⨯+ 三是拆数式，如：861318613868613)186(861387⨯+⨯=⨯+=⨯ 861318613868613)186(861385⨯-⨯=⨯-=⨯ 4、求一个数的几分之几是多少，用乘法计算，关系式是：单位“1”的量×分率= 分率的对应量解题的关键是找准单位“1”的量和所求的量的对应分率。

5、乘积是1的两个数互为倒数。

它的含义有四方面：一是两个数，二是用乘法；三是乘的结果是1，四是称呼上是相互的，注意倒数不能用等号。

6、找一个数的倒数的方法：分数：将分数的分子和分母互相调换位置。

小数：先转化成分数，再把分子分母交换位置。

整数：看成分母是1的分数，再把分子分母交换位置。

特殊数：0没有倒数；1的倒数是1第三单元 分数除法1、分数除法的意义：（1）通用的：已知两个因数的积与其中一个因数，求另一个因数是多少。

如：5432 表示已知两个因数的积是32，其中一个因数是54，求另个因数是多少。

2、分数除法的计算方法：甲数除以乙数（0除外），等于甲数乘乙数的倒数。

（被除数不变，除号变乘号，除数变倒数。

）3、四则混合运算法则：（1）在没有括号的算式里，同级运算应从左往右依次计算；异级运算应先乘除后加减。

第一单元《分数乘法》知识点1、 分数乘整数的意义与整数乘法的意义相同，都是求几个相同加数的和的简便运算。

比如：72×3 ，表示求3个72相加是多少，或者求72的3倍是多少。

2、 一个数乘分数的意义：就是求这个数的几分之几是多少。

比如：3×72 ，表示求3的72是多少。

3、 分数乘法包括：① 分数和整数相乘：整数和分子相乘的积作分子，分母不变，能约分的要先约分。

（注意：整数和分子不能约分） 比如：103×5 ，分母10和整数5约分。

② 分数和分数相乘：用分子相乘的积作分子，用分母相乘的积作分母，能约分的要先约分。

（注意：分子只能和分母约分，分子与分子，分母与分母之间不能约分） 比如：152×85 ，分子2和分母8约分，分子5和分母15约分。

③ 分数和小数相乘：可以把小数化成分数；也可以把分数化成小数；或者直接用小数和分母进行约分。

比如：85×1.6 ，可以把1.6化成1016；也可以把85化成0.625；或者直接将分母8和小数1.6约分。

4、 分数乘法的运算顺序和整数乘法相同，先算乘除，后算加减，有括号先算括号里面的。

比如：85-83×65，先算乘法，再算减法，不能先用85减去83。

5、 整数乘法的交换律、结合律和分配律，对于分数乘法也适用。

交换律：a × b = b × a结合律：（a × b ）× c = a ×（b × c ）分配律：a ×（b ＋ c ）= a × b ＋ a × c 比如：154×94＋154×95，运用乘法分配律，将两边乘法中相同的分数154提到括号外面，再乘括号中的（94＋95）。

6、 分数乘法应用题分为：① 连续求一个数的几分之几是多少。

②求比一个数多（或少）几分之几的数是多少。

（2）算术法，根据m占x的分率得，x＝m÷a/b解答已知x的a/b的c/d是m，求x的方法：（1）根据题意列方程，a/b×c/d×x＝m,解答，（2）算术法：x＝m÷a/b÷c/d16、用方程解决分数问题（二）“已知比一个数多（或少）几分之几的数是多少，求这个数”的解题方法17、用方程解决分数问题（三）已知x±y=a，又y=bx。

求x、y的方法，用bx代替y，列方程x±bx=a解出x，然后再表示出y18、用分数解决工程问题用分数来解决工程问题的解题方法与用整数来解决工程问题的解题方法相同，所用数量关系相同，即：工作总量＝工作效率×工作时间，工作效率＝工作总量÷工作时间，工作时间＝工作总量÷工作效率在用分数解决工程问题时，通常没有具体的工作总量，解题时把工作总量看作单位“1”，用单位时间内完成工作总量的几分之一表示工作效率第四单元比19、比的认识生活中两个数量之间存在”倍比“关系，例如长方形的宽高比。

两个数相除，又叫做这两个数的比比有两种写法：a:b或a/b（b不等于0），读作a比b。

“:”是比号，读作“比”，比号前面的是数是比的前项，比号后面的数是比的后项；用比的前项除以比的后项得到一个数，这个数就是比值20、求比值求比值，就是用比的前项除以比的后项，求出商。

比值是一个数，通常用分数表示，也可以用小数或整数表示21、求比中的未知项已知前项、后项、比值三者中的任意两项，都可以根据它们之间的关系求出第三项22、比与除法、分数的关系比表示两个量（或数)之间的倍比关系，除法是一种运算，它们的读法不同，表示方法也不同，除法算式不能用比表示比表示两个量（或数)之间的倍比关系，分数则是一种数，比可以写成分数形式，但分数不一定表示比，而且它们的读法也不同23、比的基本性质比的前项和后项同时乘或除以相同的数（0除外）比值不变，这叫做比的性质24、比的化简整数比的化简：方法1、把比改写成除法算式，求出商后再化成比；方法2、先将比改写成分数形式，然后约分成最简分数，再写成比；方法3、根据比的性质，把比的前后项同时除以它们的最大公因数，化成最简整数比分数比的化简方法：方法1、用比的前项除以比的后项，商用最简分数表示，再转化成比；。

六年级上册数学1-4单元知识点整理汇总第一单元《分数乘法》1．分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

2．分数乘整数的计算法则：分数乘整数，用分数的分子和整数相乘的积作分子，分母不变。

（为了计算简便，能约分的要先约分，然后再乘。

）注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

3．一个数与分数相乘，可以看作是求这个数的几分之几是多少。

4．分数乘分数的计算法则：分数乘分数，用分子相乘的积作分子，分母相乘的积作分母。

（为了计算简便，可以先约分再乘。

）注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

5．整数乘法的交换律、结合律和分配律，对分数乘法同样适用。

乘法交换律：a × b = b × a乘法结合律：( a × b )×c = a × ( b × c )乘法分配律：（ a + b ）×c = a c + b c a c + b c = （ a + b ）×c 6．一个数（0除外）乘以一个真分数，所得的积小于它本身。

一个数（0除外）乘以一个假分数，所得的积等于或大于它本身。

一个数（0除外）乘以一个带分数，所得的积大于它本身。

7．分数应用题一般解题步骤。

（1）找出含有分率的关键句。

（2）找出单位“1”的量（以后称为“标准量”）找单位“1”：在分率句中分率的前面；或“是”、“占”、“比”、“相当于”的后面（3）画出线段图，标准量与比较量是整体与部分的关系画一条线段即可，标准量与比较量不是整体与部分的关系画两条线段即可。

（4）根据线段图写出等量关系式：标准量×对应分率=比较量。

求一个数的几倍：一个数×几倍；求一个数的几分之几是多少：一个数×。

写数量关系式技巧：（1）“的”相当于“×”“占”、“是”、“比”相当于“ =”（2）分率前是“的”：单位“1”的量×分率=分率对应量（3）分率前是“多或少”的意思：单位“1”的量×（1分率）=分率对应量（5）根据已知条件和问题列式解答。

六年级上册数学期末知识点复习第一单元分数乘法(一)分数乘法的意义1、分数乘整数:分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数和得简便运算。

例如:512X6，表示:6 个512相加是多少，还表示512的6倍是多少。

2、一个数(小数、分数、整数)乘分数:一个数乘分数的意义与整数乘法的意义不相同,是表示这个数的几分之几是多少。

例如:6x512，表示:6的512是多少。

27x512，表示:27的512是多少。

(二)分数乘法的计算法则1、整数和分数相乘:整数和分子相乘的积作分子，分母不变。

2、分数和分数相乘:分子相乘的积作分子，分母相乘的积作分母。

3、注意:能约分的先约分，然后再乘，得数必须是最简分数。

当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

(三)分数大小的比较:1、一个数(0除外)乘以一个真分数，所得的积小于它本身。

一个数(0除外)乘以一个假分数，所得的积等于或大于它本身。

一个数(0除外)乘以一个带分数，所得的积大2、如果几个不为0的数与不同分数相乘的积相等，那么与大分数相乘的因数反而小，与小分数相乘的因数反而大。

(四)解决实际问题。

1、分数应用题一般解题步行骤。

(1)找出含有分率的关键句。

(2)找出单位“1”的量(3)根据线段图写出等量关系式:单位“1”的量X对应分率=对应量。

(4)根据已知条件和问题列式解答。

2、乘法应用题有关注意概念。

(1)乘法应用题的解题思路:已知一个数，求这个数的几分之几是多少?(2)找单位“1”的方法:从含有分数的关键句中找，注意“的”前“比”后的规则。

当句子中的单位“1”不明显时,把原来的量看做单位“1”。

(3)甲比乙多几分之几表示甲比乙多的数占乙的几分之几甲比乙少几分之几表示甲比乙少数占乙的几分之几。

(4)在应用题中如:小湖村去年水稻的亩产量是750千克今年水稻的亩产量是800千克，增产几分之几?题目中的“增产”是多的意思,那么谁比谁多,应该是“多比少多”，“多”的是指800千克，“少”的是指750千克，即800千克比750千克多几分之几，结合应用题的表达方式，可以补充为“今年水稻的亩产量比去年水稻的亩产量多几分之几?，(5)“增加”、“提高”、“增产”等蕴含“多”的意思，“减少”、“下降”、“裁员”等蕴含“少”的意思，“相当于”、“占”、“是”、“等于”意思相近。

人教版小学数学六年级下册第一单元1.11《分数乘法整理与复习》教学设计教学内容：人教版小学数学六年级下册第一单元《分数乘法整理与复习》。

教学目标：1.使学生掌握分数乘法的计算方法，并能运用这个方法进行相关计算。

使学生能分辨清楚先乘后加减的运算顺序，并能熟练地应用乘法运算定律进行简便计算。

2.引导学生准确地找到单位“1”，并能熟练地解答一步和二步的乘法应用题3.通过练习培养学生认真仔细的学习习惯。

教学重点：对所学知识回忆和整理。

教学难点：通过整理和复习，感受知识的内在联系。

教学过程：师：首先，请大家回忆一下，本单元我们都学习了什么？我们需要整理什么？又该怎样复习呢？对，我们要看标题、复习例题、找出知识点、注意关键与提示、重温分析与解题思路等等。

下面，就请结合你手中的教材，将你的头脑库中所储存的知识点都检索出来吧！师：好，整理完了吗？现在，请大家和老师一起来回顾本单元所学习的内容，看看你还有没有新的思考和补充。

一、知识回顾师：通过刚刚大家的整理我们知道，分数乘法这个单元的内容主要可以分为三个方面，分数乘法的意义、分数乘法的计算和利用分数乘法解决实际问题。

分数乘法的意义是什么呢？师：是的，就像你们整理的那样，包括两个方面，一是教材例1中所讲的分数乘整数，它表示求几个相同加数的和的简便运算。

二是教材中例2和例3中所讲的，一个数乘分数，它表示求一个数的几分之几是多少。

从这几道例题中我们很清楚的知道了：一个数乘几分之几表示的是求这个数的几分之几是多少。

所以，一个数的几分之几都可以用这个数乘上几分之几来表示。

师：通过前面的3个例题，我们知道了分数乘整数：用分子乘整数的积作分子，分母不变。

分数乘分数：用分子相乘的积作分子，用分母相乘的积作分母。

通过例4的学习，我们知道了为了计算简便，能约分的，要先约分再计算。

师：在例5中，我们又探究了分数与小数相乘的一些方法，比如可以把分数化成小数计算，或者把小数化成分数计算，也可以直接“约分”。

分数乘法(思维导图+知识梳理+典例分析+高频真题+答案解析)【分数乘法-知识点归纳】1、分数乘法的意义：分数乘法的意义与整数乘法的意义相同，就是求几个相同加数和的简便运算．2、乘积是1的两个数叫做互为倒数．3、分数乘法法则：（1）带分数乘法：先把带分数化成假分数，然后再乘．结果是假分数时，要把假分数化成带分数或整数．（2）（2）分数乘以分数：用分子相乘的积作为分子，用分母相乘的积作为分母．为了使计算简便，在计算的过程中，能够约分的，要约分．（3）分数乘以整数或整数乘以分数：由于任何整数（0除外）都可以化成分母是1的假分数，分数乘以整数或整数乘以分数，都可以转化成分数乘以分数的形式．因此，在计算中，是用分数的分子和整数相乘的积作为分子，分母不变．在乘的过程中，如果有可以约分的数，可以先约分，这样，可以使计算的数字缩小，从而使计算变得简便．【分数乘整数-知识点归纳】1、分子乘整数，可以求出一共有多少个这样的分数单位，而分数单位的个数其实就是分子乘整数的积，因此整数乘分子作分子。

求几个分数单位的和，分数单位不变，也就是分母不变。

2、分数乘整数的意义：分数乘整数，也是表示几个相同加数相加，与整数乘法的意义相同。

3、分数乘整数的计算方法：分数乘整数，用分子乘整数的积作分子，分母不变。

其实就是计算分数单位的个数。

【整数乘分数-知识点归纳】1、一个数乘分数的意义就是求一个数的几分之几是多少。

2、“一个数乘分数”指的是第二个因数必须是分数，不能是整数。

（第一个因数是什么都可以）3、方法总结；（1）、整数与分数相乘，用分数的分子与整数相乘，分母不变；（2）、计算时能约分的可以先约分再计算出结果。

【分数乘分数-知识点归纳】分数乘法的计算法则1、整数和分数相乘：整数和分子相乘的积作分子，分母不变。

2、分数和分数相乘：分子相乘的积作分子，分母相乘的积作分母。

【典例1】在“世界无烟日”健康知识竞赛中，小星答对了50道题，小铭答对的题数比小星少15。

六年级上册数学教案第一单元分数乘法整理和复习人教版今天，我们来进行六年级上册数学的第一单元——分数乘法的整理和复习。

这个单元主要是对分数乘法的知识进行梳理和巩固，让学生能够灵活运用分数乘法的法则，解决实际问题。

一、教学内容我们使用的教材是人教版六年级上册的数学教材。

今天我们将复习第97页至第100页的内容，包括分数乘法的法则、计算方法和应用。

二、教学目标通过今天的复习，我希望学生们能够掌握分数乘法的计算法则，能够熟练地进行分数乘法的计算，并且能够将分数乘法应用到实际问题中。

三、教学难点与重点今天教学的重点是分数乘法的计算法则和应用，难点是如何将实际问题转化为分数乘法的问题。

四、教具与学具准备为了帮助学生们更好地理解和掌握分数乘法的知识，我准备了PPT 和一些实际的例子。

五、教学过程六、板书设计板书设计如下：分数乘法法则：1. 分子相乘的积做分子2. 分母相乘的积做分母七、作业设计(1) 1/2 × 3/4(2) 5/6 × 2/3(3) 4/5 × 7/8答案：(1) 3/8(2) 5/9(3) 28/40 = 7/10八、课后反思及拓展延伸通过今天的复习，我发现大部分学生们对于分数乘法的计算法则掌握得比较好，但是在将实际问题转化为分数乘法问题时还有一定的困难。

在今后的教学中，我将继续强调实际问题的转化，帮助学生们更好地应用分数乘法的知识。

同时，我也会鼓励学生们在课后进行更多的练习，巩固他们的分数乘法知识，并将分数乘法应用到更多的实际问题中。

我相信通过不断的练习和应用，学生们能够更好地掌握分数乘法的知识。

重点和难点解析在上述教案中，有几个重点和难点是我认为需要特别关注的。

教学内容的选择和安排是非常重要的。

在复习分数乘法时，我选择了与学生们生活密切相关的实际问题，这样能够激发他们的兴趣，也能够帮助他们更好地理解和应用分数乘法的知识。

通过展示PPT和实际的例子，我能够更直观地呈现分数乘法的问题，让学生们能够更清晰地理解分数乘法的计算法则。

章节复习讲义（人教版）2021-2022学年人教版数学六年级上册章节复习精讲精练第一单元《分数乘法》知识互联网知识导航知识点一：分数乘整数1.分数乘整数的意义分数乘整数的意义与整数乘法的意义相同，都是求几个相同加数的和的简便2.分数乘整数的计算方法分数乘整数，用分数的分子和整数相乘的积作分子，分母不变。

3.分数乘整数的简便算法能约分的可以先约分，再计算，这样可以简便些。

知识点二：分数乘分数1.分数乘分数的意义分数乘分数，表示求这个数的几分之几是多少。

2.分数乘分数的计算方法用分子相乘的积作分子，用分母相乘的积作分母。

3.分数乘法的简便运算能约分的要先约分，后计算，计算结果必须是最简分数或整数。

知识点三：小数乘分数1. 能约分的先约分再计算比较简便。

2. 可以把小数转化成分数来计算；如果分数能化成有限小数，也可以把分数化成小数来计算。

知识点四：分数乘法运算定律1.应用乘法的运算定律时要做到：一看符号：看运算符号是不是符合运算定律的要求；二看数：看参与计算的数是否符合简便计算；三选定律：根据参与运算的数和符号，选择合适的运算定律；四计算：运用运算定律进行计算。

2.连续求一个数的几分之几是多少的实际问题有两种解法：（1）用已知量（原始单位“1”的量）依次乘已知分率。

（2）先把各分率按顺序相乘，求出所求问题占原始单位“1”的量的分率，再用原始单位“1”的量乘这个分率。

（2.1）解题关键是明确每一步中谁是单位“1”。

（2.2）每一步中的数量关系是：单位“1”的量×比较量占单位“1”的几分之几＝比3. 求比一个数多(或少)几分之几的数是多少的问题；已知一个部分量是总量的几分之几，求另一个部分量的问题。

两类问题都可以用以下两种解法：（1）单位“1”的量+单位“1”的量×这个数量比单位“1”的量多(或少)几分之几=这个数量（2）单位“1”的量× (1+这个数量比单位“1”的量多(或少)几分之几)=这个数量一、精挑细选（共5题；每题2分，共10分）1．(本题2分)（2021·寻乌县教育局教学研究室六年级课时练习）41441421212121337337⎛⎫++⨯=⨯+⨯+⨯ ⎪⎝⎭，运用了（ ）。