下载文档原格式
动点之平行四边形问题(含特殊四边形)【例5】(2019·广东中考模拟)如图，点O 是平面直角坐标系的原点，点3)，AC ⊥OA 与x 轴的交点为C ．动点M 个单位长度由点A 向点O 运动．同时，动点N 以每秒3个单位长度由点O 向点C 运动，当一动点先到终点时，另一动点立即停止运动．(1)写出∠AOC 的值；(2)用t 表示出四边形AMNC 的面积；(3)求点P 的坐标，使得以O 、N 、M 、P 为顶点的四边形是特殊的平行四边形？【答案】(1)30°；(2)29(02)4t t <<；(3)33P 3t t,t 22⎛⎫-- ⎪ ⎪⎝⎭. 【解析】(1)如图1中，作AH ⊥OC 于H ．在Rt △AOH 中，解直角三角形求出∠AOH 即可解决问题．(2)作MK ⊥BC 于K ．根据S 四边形AMNC ＝S △OAC ﹣S △OMN ，计算即可．(3)分别考虑以OM ，ON ，MN 为平行四边形的对角线，利用平行四边形的性质求解即可．【详解】解：(1)如图1中，作AH ⊥OC 于H ．∵3)，∴OHAH＝3，∴tan∠AOH＝AHOH，∴∠AOH＝60°，∵OA⊥AC，∴∠OAC＝90°，∴∠ACO＝30°．(2)作MK⊥BC于K．在Rt△AOH中，∵OH∠OAH＝30°，∴OA＝2OH＝在Rt△AOC中，∵∠AOC＝30°，OA＝∴AC＝6，∵OM，∴MK＝OM•sin60°＝32t，∴S四边形AMNC＝S△OAC﹣S△OMN＝12•OA•AC﹣12•ON•MKa＝12×6﹣12×3t×32t＝94t2(0＜t＜2)．(3)当四边形CNMP1是平行四边形时，P1(2t﹣3t，32t)．当四边形ONP2M是平行四边形时，P2(t+3t，32t)．当四边形OMNP3是平行四边形时，P3(3t﹣2t，﹣32t)．【点睛】本题属于四边形综合题，考查了四边形的面积，平行四边形的性质，解直角三角形等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题，属于中考常考题型．【变式5-1】(2019·江西中考真题)在图1，2，3中，已知▱ABCD，∠ABC=120°，点E为线段BC上的动点，连接AE，以AE为边向上作菱形AEFG，且∠EAG=120°．(1)如图1，当点E与点B重合时，∠CEF=________°；(2)如图2，连接AF．①填空：∠FAD_________∠EAB(填“>”，“<”，“=”)；②求证：点F在∠ABC的平分线上；(3)如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求BCAB的值．【答案】(1)60°；(2)① =，②见解析；(3)4【解析】(1)根据菱形的性质计算；(2)①证明∠DAB=∠FAE=60°，根据角的运算解答；②作FM⊥BC于M，FN⊥BA交BA的延长线于N，证明ΔAFN≅ΔEFM，根据全等三角形的性质得到FN=FM，根据角平分线的判定定理证明结论；(3)根据直角三角形的性质得到GH=2AH，证明四边形ABEH为菱形，根据菱形的性质计算，得到答案．【详解】解：(1)∵四边形AEFG是菱形，∴∠AEF=180°−∠EAG=60°，∴∠CEF=∠AEC−∠AEF=60°，故答案为：60°；(2)①∵四边形ABCD是平行四边形，∴∠DAB=180°−∠ABC=60°，∵四边形AEFG是菱形，∠EAG=120°，∴∠FAE=60°，∴∠FAD=∠EAB，故答案为：=；②作FM⊥BC于M，FN⊥BA交BA的延长线于N，则∠FNB=∠FMB=90°，∴∠NFM=60°，又∠AFE=60°，∴∠AFN=∠EFM，∵EF=EA，∠FAE=60°，∴ΔAEF为等边三角形，∴FA=FE，在ΔAFN和ΔEFM中，{∠AFN =∠EFM ∠FNA =∠FME FA =FE，∴ΔAFN ≅ΔEFM(AAS)，∴FN =FM ，又FM ⊥BC ，FN ⊥BA ，∴点F 在∠ABC 的平分线上；(3)∵四边形AEFG 是菱形，∠EAG =120°，∴∠AGF =60°，∴∠FGE =∠AGE =30°，∵四边形AEGH 为平行四边形，∴GE//AH ，∴∠GAH =∠AGE =30°，∠H =∠FGE =30°，∴∠GAH =90°，又∠AGE =30°，∴GH =2AH ，∵∠DAB =60°，∠H =30°，∴∠ADH =30°，∴AD =AH =GE ，∵四边形ABEH 为平行四边形，∴BC =AD ，∴BC =GE ，∵四边形ABEH 为平行四边形，∠HAE =∠EAB =30°，∴平行四边形ABEH 为菱形，∴AB =AH =HE ，∴GE =3AB ，∴BC AB =3．【点睛】本题考查了菱形的性质、平行四边形的性质、全等三角形的判定和性质.掌握全等三角形的判定定理和性质定理、菱形的性质、直角三角形的性质是解题的关键．【变式5-2】(2019·湖南中考真题)如图，二次函数213y x bx c=-++的图象过原点，与x轴的另一个交点为() 8,0(1)求该二次函数的解析式；(2)在x轴上方作x轴的平行线1y m=，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；(3)在(2)的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒(0t>)．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．【答案】(1)21833y x x=-+；(2)当矩形ABCD为正方形时，m的值为4；(3)以A、E、F、Q四点为顶点构成的四边形能为平行四边形，t的值为4或6.【解析】(1)根据点的坐标，利用待定系数法即可求出二次函数的解析式；(2)利用二次函数图象上点的坐标特征求出点A，B的坐标，进而可得出点C，D的坐标，再利用正方形的性质可得出关于m的方程，解之即可得出结论；(3)由(2)可得出点A，B，C，D的坐标，根据点A，C的坐标，利用待定系数法可求出直线AC的解析式，利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征可求出点E，F的坐标，由AQ EF//且以A、E、F、Q四点为顶点的四边形为平行四边形可得出AQ EF =，分0t 4<≤，4t 7<≤，7t 8<≤三种情况找出AQ ，EF 的长，由AQ EF =可得出关于t 的一元二次方程，解之取其合适的值即可得出结论．【详解】(1)将()00，，()80，代入21y x bx c 3=-++，得：064803c b c =⎧⎪⎨-++=⎪⎩， 解得830b c ⎧=⎪⎨⎪=⎩，∴该二次函数的解析式为218y x x 33=-+． (2)当y m = 时，218x x m 33-+=，解得：1x 4=，2x 4=∴点a 的坐标为(4，m)，点b 的坐标为(4，m)，∴点d 的坐标为(4，0)，点c 的坐标为(4，0)．∵矩形abcd 为正方形，∴(44m=， 解得：1m 16=-，(舍去)，2m 4=．∴当矩形ABCD 为正方形时，m 的值为4．(3)以A 、E 、F 、Q 四点为顶点构成的四边形能为平行四边形．由(2)可知：点A 的坐标为()24，，点B 的坐标为()64，，点C 的坐标为()60，，点D 的坐标为()20，．设直线AC 的解析式为()y kx a k 0=+≠， 将()a 24，，()c 60，代入y kx a =+，得2460k a k a +=⎧⎨+=⎩，解得16k a =-⎧⎨=⎩，∴直线ac 的解析式为y x 6=-+．当x 2t =+时，221814y x x t t 43333=-+=-++ ，y x 6t 4=-+=-+∴点E 的坐标为(2t +，214t t 433-++)，点F 的坐标为(2t +，t 4-+-t+4)．∵以A 、E 、F 、Q 四点为顶点构成的四边形为平行四边形，且AQ ΕF // ，∴AQ EF =，分三种情况考虑：①当0t 4<≤时，如图1所示，AQ t =，EF=()221417t t 4t 4t t 3333-++--+=-+， ∴217t t t 33=-+，解得：1t 0=(舍去)，2t 4=；②当4t 7<≤时，如图2所示，AQ t 4=-，EF=()221417t t 4t 4t t 3333-++--+=-+， ∴217t 4t t 33-=-+， 解得：3t 2=-(舍去)，4t 6=；7t 8<≤,AQ t 4=-, EF=()221417t t 4t 4t t 3333-++--+=--，217t 4t t 33∴-=-，解得5t 5=舍去)，6t 5=舍去)综上所述，当以A 、E 、F 、Q 四点为顶点构成的四边形为平行四边形时，t 的值为4或6【点睛】本题考查了待定系数法求二次函数解析式、二次函数图象上点的坐标特征、正方形的性质、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及平行四边形的性质，解题的关键是：(1)根据点的坐标，利用待定系数法求出二次函数解析式；(2)利用正方形的性质，找出关于m 的方程；(3)分0t 4<≤，4t 7<≤，7t 8<≤三种情况，利用平行四边形的性质找出关于t 的一元二次方程．【变式5-3】．如图，在平面直角坐标系中，AOB ∆的顶点O 是坐标原点，点A 坐标为()1,3，A 、B 两点关于直线y x =对称，反比例函数()0k y x x =>图象经过点A ，点P是直线y x =上一动点.(1)B 点的坐标为______；(2)若点C 是反比例函数图象上一点，是否存在这样的点C ，使得以A 、B 、C 、P 四点为顶点的四边形是平行四边形？若存在，求出点C 坐标；若不存在，请说明理由；(3)若点Q 是线段OP 上一点(O 不与O 、P 重合)，当四边形AOBP 为菱形时，过点Q 分别作直线OA 和直线AP 的垂线，垂足分别为E 、F ，当QE QF QB ++的值最小时，求出Q 点坐标.【答案】(1)(3，1)；(2)12)C ，22)C ，3C ；(3)(2，2). 【解析】(1)根据点(a ，b)关于y=x 对称的点的坐标为(b ，a)直接写出答案即可；(2)首先求得反比例函数的解析式，然后设P(m ，m)，分若PC 为平行四边形的边和若PC 为平行四边形的对角线两种情况分类讨论即可确定点C 的坐标；(3)连接AQ ，设AB 与PO 的交点为D ，利用四边形AOBP 是菱形，得到S △AOP=S △AOQ+S △APQ ，从而得到12PO•AD=12AO•QE+12AP•QF ，确定QE+QF=•PO ADAO 为定值，从而求解．【详解】解：(1)B 点的坐标为(3，1)；(2)∵反比例函数()0k y x x =>图象经过点A(1，3)， ∴k=1×3=3，∴反比例函数的解析式为3y x =， 点P 在直线y=x 上，∴设P(m ，m)①PC 为平行四边形的边，∵点A 的横坐标比点B 的横坐标小2，点A 的纵坐标比点B 的纵坐标大2， ∴点C 在点P 的下方，则点C 的坐标为(m+2，m-2)如图1，若点C 在点P 的上方，则点C 的坐标为(m-2，m+2)如图2，把C(m+2，m-2)代入反比例函数的解析式得：m =，∵m ＞0，∴m =，∴12)C +同理可得另一点22)C ，②若PC为平行四边形的对角线，如图3，∵A、B关于y=x对称，∴OP⊥AB此时点C在直线y=x上，且为直线y=x与双曲线的3yx=交点，由3y xyx=⎧⎪⎨=⎪⎩解得：11xy⎧=⎪⎨=⎪⎩22xy⎧=⎪⎨=⎪⎩(舍去)，∴3C，综上所述，满足条件的点C有三个，坐标分别为：12) C，22)C，3C；(3)连接AQ，设AB与PO的交点为D，如图4，∵四边形AOBP是菱形，∴AO=AP∵S△AOP=S△AOQ+S△APQ，∴12PO•AD=12AO•QE+12AP•QF∴QE+QF=•PO ADAO为定值，∴要使QE+QF+QB的值最小，只需QB的值最小，当QB⊥PO时，QB最小，所以D点即为所求的点，∵A(1，3)，B(3，1)∴D(2，2)，∴当QE+QF+QB的值最小时，Q点坐标为(2，2)．【点睛】本题是对反比例函数的综合知识的考查，熟练掌握反比例，四边形知识及分类讨论的数学思想是解决本题的关键，难度较大．。
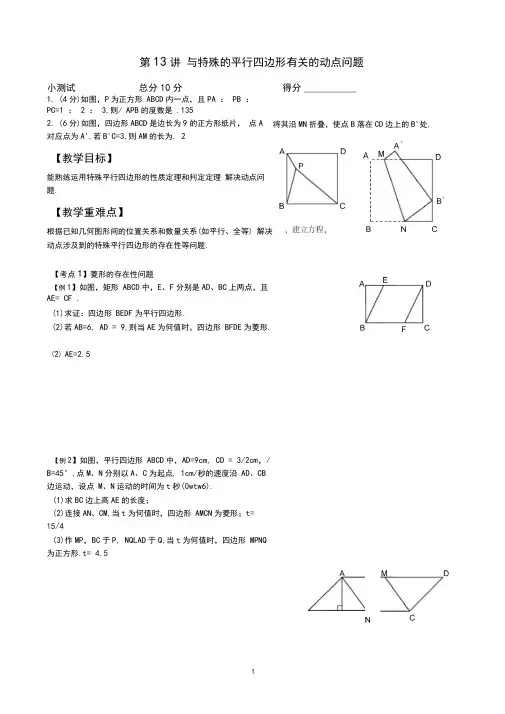
第13讲 与特殊的平行四边形有关的动点问题1. (4分)如图，P 为正方形 ABCD 内一点，且PA ： PB ：PC=1 ： 2 ： 3,则/ APB 的度数是 .1352. (6分)如图，四边形ABCD 是边长为9的正方形纸片， 点A对应点为A',若B'C=3,则AM 的长为. 2【教学目标】能熟练运用特殊平行四边形的性质定理和判定定理 解决动点问题.【教学重难点】根据已知几何图形间的位置关系和数量关系(如平行、全等) 解决动点涉及到的特殊平行四边形的存在性等问题. 【考点1】菱形的存在性问题【例1】如图，矩形 ABCD 中，E 、F 分别是AD 、BC 上两点，且AE= CF .(1)求证：四边形 BEDF 为平行四边形.(2)若AB=6, AD = 9,则当AE 为何值时，四边形 BFDE 为菱形. ⑵ AE=2.5【例2】如图，平行四边形 ABCD 中，AD=9cm, CD = 3/2cm ，/B=45°,点M 、N 分别以A 、C 为起点, 1cm/秒的速度沿 AD 、CB边运动，设点 M 、N 运动的时间为t 秒(0wtw6).(1)求BC 边上高AE 的长度；(2)连接AN 、CM,当t 为何值时，四边形 AMCN 为菱形；t= 15/4(3)作MP ，BC 于P, NQLAD 于Q,当t 为何值时，四边形 MPNQ为正方形.t= 4.5小测试 总分10分 得分 ___________将其沿MN 折叠，使点B 落在CD 边上的B'处,【例3】如图，O为坐标原点，四边形OABC为矩形，A (10, 0), C (0, 4), D为OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动.(1)当t为何值时，四边形PODB是平行四边形？t=5s(2)在线段PB上是否存在一点Q,使得ODQP为菱形？若存在，求t的值；若不存在，请说明理由;(3)当^ OPD为等腰三角形时，写出点P的坐标(不必写过程).⑵ t= 3s y j,(3) P i (3, 4), P2 (2.5, 4), P3 (2, 4), P4 (8, 4) PC --- *-------------- B.----------------------- ■D Ax【考点2】矩形的存在性问题【例4】如图，平行四边形ABCD的对角线AC、BD相交于点同时分别以2cm/s的速度从点A、C出发在线段AC上运动.O, AC = 20cm, BD=12cm,两动点E、F(1)求证：当E、F运动过程中不与点。
平行四边形中的动点问题专题复习【精品】于HDHC是等腰三角形CH=DH=2QC- DH=CQ-CH=13t-2=1.t=1XXX为1s时，△DQC是等腰三角形．该问题的解答过程中，首先根据题目条件列出方程，然后通过解方程得到具体的数值解，最后根据几何知识进行推导和证明。
在变式题中，需要根据题目要求对原问题进行适当的变形和推广，然后按照相同的解题思路进行求解。
没有明显的格式错误和有问题的段落。
专项一：平行四边形中的动点问题1.在四边形ABCD中，AD∥BC，且AD＞BC，BC＝6cm，动点P，Q分别从A，C同时出发，P以1cm/s的速度由A向D运动，Q以2cm/s的速度由C向B运动，则2s后四边形ABQP为平行四边形。
2.在等边△ABC中，BC＝6cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，点F从点B出发沿射线BC以2cm/s的速度运动。
如果点E，F同时出发，设运动时间为t（s），当t＝2或6时，以A，C，E，F为顶点的四边形是平行四边形。
3.在平面直角坐标系中，点A，B的坐标分别为A(0，a)，B(b，a)，且a，b满足(a－3)2＋|b－6|＝0.现将线段AB向下平移3个单位长度，再向左平移2个单位长度，得到线段CD，点A，B的对应点分别为点C，D。
连接AC，BD。
1) 求点C，D的坐标及四边形ABDC的面积；2) 在y轴上是否存在一点M，使三角形MCD的面积与四边形ABDC的面积相等？若存在，求出点M的坐标，若不存在，试说明理由；3) 点P是直线BD上的一个动点，连接PA，PO，当点P在直线BD上移动时(不与B，D重合)，直接写出∠BAP，∠DOP，∠APO之间满足的数量关系。
解：(1) 因为(a－3)2＋|b－6|＝0。
所以a－3＝0，b－6＝0，解得a＝3，b＝6.所以A(0，3)，B(6，3)。
因为将点A，B分别向下平移3个单位长度，再向左平移2个单位长度，所以C(－2，0)，D(4，0)。
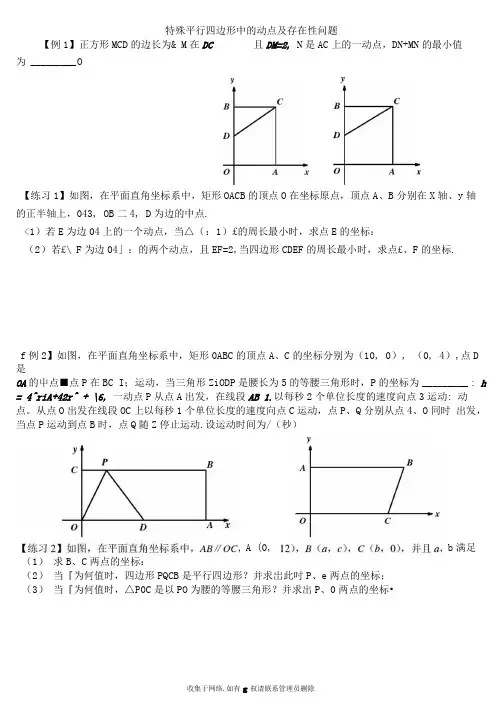
特殊平行四边形中的动点及存在性问题【例1】正方形MCD 的边长为& M 在DC 且DM=2, N 是AC 上的一动点，DN+MN 的最小值 为 _________ O【练习1】如图，在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在X 轴、y 轴 的正半轴上，043, OB 二4, D 为边的中点.<1）若E 为边04上的一个动点，当△（：1）£的周长最小时，求点E 的坐标：（2）若£\ F 为边04」：的两个动点，且EF=2,当四边形CDEF 的周长最小时，求点£、F 的坐标. f 例2】如图，在平面直角坐标系中，矩形0ABC 的顶点A 、C 的坐标分别为（10, 0）, （0, 4）,点D 是OA 的屮点■点P 在BC I ；运动，当三角形ZiODP 是腰长为5的等腰三角形时，P 的坐标为 _________ : h = 4^riA+42r^ + \6, 一动点P 从点A 出发，在线段AB 1.以每秒2个单位长度的速度向点3运动: 动点。
从点O 出发在线段OC 上以每秒1个单位长度的速度向点C 运动，点P 、Q 分别从点4、O 同时 出发，当点P 运动到点B 时，点Q 随Z 停止运动.设运动时间为/（秒）（1） 求B 、C 两点的坐标：（2） 当『为何值时，四边形PQCB 是平行四边形？并求岀此吋P 、e 两点的坐标；（3） 当『为何值时，△P0C 是以PO 为腰的等腰三角形？并求出P 、0两点的坐标•A (0,b 满足【例3】（1）如图，矩形ONEF的对角线相交于点ON、OF分别在X轴和y轴上，0为坐标原点，点E的坐标为（4, 3）,则点M的坐标为_________________ ；（2）在直角坐标系屮，有A （-1, 2）, B（3, 1）. C <1, 4）三点，另有一点Q与点A、B、C构成平行四边形的顶点，求点D的坐标.【练习3】如图，四边形ABCD为矩形，C点在犬轴上，A点在y轴上，D点坐标是（0, 0）, B点坐标是（3, 4）,矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD. AB 1；,且尸点的坐标是（2, 4）.（1）求G点坐标：（2）求直线EF解析式；（3）点N在*轴上，直线EF上是否存在点M,使以M、N、F、G为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由.【例4】在RgB C屮，Z8=90。
初二平行四边形动点练习题平行四边形是初中数学中的重要概念之一，对于初二学生来说，掌握平行四边形的性质和相关定理是非常重要的。
本文将介绍一些初二平行四边形的动点练习题，帮助同学们巩固对平行四边形的理解和运用。
题一：在平行四边形ABCD中，点E是AD的中点，连接BE交AC于点F，若AB＝6cm，BC＝8cm，则证明DE＝2cm。
解答：首先，根据平行四边形的性质，我们知道对角线互相平分。
可以观察到平行四边形的一条对角线AD被点E平分，即AE＝ED。
我们需要证明DE＝2cm。
由于平行四边形ABCD的对角线互相平分，所以线段BF也被点E 平分，即BE＝EF。
根据题意可知，AB＝6cm，BC＝8cm，因此AC＝AB＋BC＝6cm＋8cm＝14cm。
根据线段等分定理可得：EF：FC＝EA：AC代入已知长度得：EF：FC＝AE：AC3：FC＝3：14根据比例关系可以得出FC＝14/3 cm。
又因为BE＝EF，所以线段BE的长度也为14/3 cm。
根据平行四边形的性质，DE＝BA＝BE－AE。
代入已知长度得：DE＝14/3 cm－6cmDE＝2cm故证明了DE＝2cm。
题二：在平行四边形ABCD中，E为AD上任意一点，F为BC上任意一点。
连接CF交BE于点G，若BE＝2x，EG＝x+3，CF＝x+4，证明AD＝3x+7。
解答：在平行四边形ABCD中，我们要证明AD＝3x+7。
首先，我们需要找到平行四边形内部的有关线段长度。
通过观察，我们可以看出线段BE和线段EG之间存在特定关系。
根据题意，我们知道BE＝2x，EG＝x+3，代入得：BG＝BE－EG＝2x－(x+3)＝x－3。
同理，我们可以确定线段CF和线段FG之间的关系。
根据题意，我们知道CF＝x+4，代入得：CG＝CF－FG＝x+4－(x－3)＝7。
现在我们需要确定线段AD的长度。
由于平行四边形ABCD的对角线互相平分，所以线段BE也被点G 平分，即BG＝1/2BE＝x－3/2。
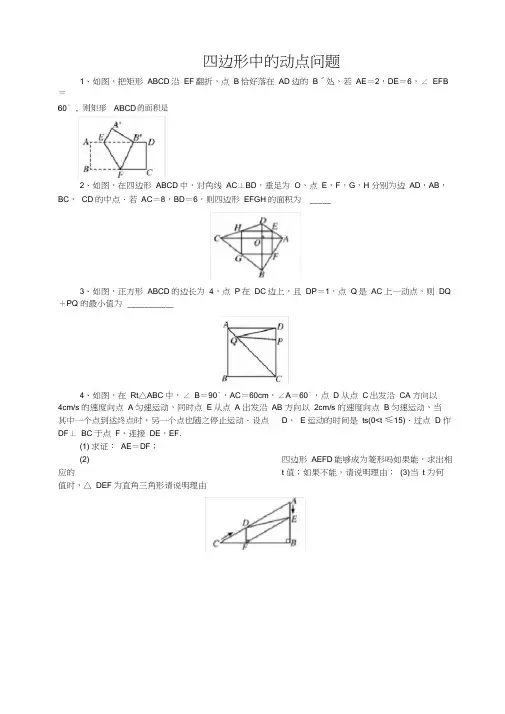
四边形中的动点问题1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠ EFB ＝2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H 分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH的面积为 _____3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ ＋PQ 的最小值为___________4、如图，在Rt△ABC中，∠ B＝90°，AC＝60cm，∠A＝60°，点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动，同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts(0<t ≤15)．过点 D 作DF⊥ BC于点F，连接DE，EF.(1) 求证：AE＝DF；(2) 四边形AEFD能够成为菱形吗如果能，求出相应的t 值；如果不能，请说明理由；(3)当t 为何值时，△ DEF为直角三角形请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点 A 出发沿射线AG以1cm/s 的速度运动，同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动，设运动时间为t.（1）连接EF，当EF经过AC边的中点 D 时，（1）求证：△ ADE≌△ CDF；：（2）当t 为____ s 时，四边形ACFE是菱形；6、在菱形ABCD中，∠ B=60°，点E在射线BC上运动，∠ EAF=60°，点 F 在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点 E 在BC的延长线上时（如图2），线段EC、CF、AB 有怎样的相等关系写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠ DAB=60°，点E是AD边的中点．点M 是AB边上一动点不与点 A 重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN 是平行四边形；（2）填空：①当AM 的值为____ 时，四边形AMDN 是矩形；②当AM 的值为____ 时，四边形AMDN 是菱形．8、如图，△ ABC中，点O 是边AC上一个动点，过O 作直线MN ∥BC，设MN 交∠ BCA的平分线于点E，交∠ BCA 的外角平分线于点F．（1）探究：线段OE与OF 的数量关系并加以证明；（2）当点O 运动到何处，且△ ABC满足什么条件时，四边形AECF是正方形（3）当点O 在边AC上运动时，四边形BCFE会是菱形吗若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD 作垂线，垂足分别为E、F．（1）BD的长是___ ；（2）连接PC，当PE+PF+PC取得最小值时，此时PB 的长是__10、如图，∠ MON=90°，矩形ABCD的顶点A、B分别在边OM，ON 上，当B在边ON 上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O 的最大距离为_____ ．11、如图，已知矩形ABCD，AD=4，CD=10，P 是AB上一动点，M、N、E分别是PD、PC、CD的中点．（1）求证：四边形PMEN 是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN 是菱形；（3）四边形PMEN有可能是矩形吗若有可能，求出AP 的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F 是AC上两动点，分别从A，C两点以相同的速度向C、A 运动，其速度为／s。
动点问题练习题1．（宁夏回族自治区）已知：等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．1、线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积； （2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．2．如图，在四边形ABCD中，3545AD BC AD DC AB B ====︒∥，，，．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒． （1）求BC 的长．（2）当MN AB ∥时，求t 的值．（3）试探究：t 为何值时，MNC △为等腰三角形．CP Q BA M N C1． 如图，在平面直角坐标系中，在四边形OABC 中，OA ∥BC ，点A 的坐标为(6，0)，点B 的 坐标为(4，3)，点C 在y 轴的正半轴上．动点M 在OA 上运动，从O 点出发到A 点；动点N 在AB 上运动，从A 点出发到B 点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t (秒)． (1)求线段AB 的长；当t 为何值时，MN ∥OC ？(2)设△CMN 的面积为S ，求S 与t 之间的函数解析式， 并指出自变量t 的取值范围；S 是否有最小值？若有最小值，最小值是多少？(3)连接AC ，那么是否存在这样的t ，使MN 与AC 互相垂直？ 若存在，求出这时的t 值；若不存在，请说明理由． 2．（河北卷）如图，在Rt △ABC 中，∠C ＝90°，AC ＝12，BC ＝16，动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动，动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动．P ，Q 分别从点A ，C 同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ 关于直线PQ 对称的图形是△PDQ ．设运动时间为t （秒）． （1）设四边形PCQD 的面积为y ，求y 与t 的函数关系式； （2）t 为何值时，四边形PQBA 是梯形？（3）是否存在时刻t ，使得PD ∥AB ？若存在，求出t 的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t ，使得PD ⊥AB ？若存在，请估计t 的值在括号中的哪个时间段内（0≤t ≤1；1＜t ≤2；2＜t ≤3；3＜t ≤4）；若不存在，请简要说明理由．3．（山东济宁）如图，A 、B 分别为x 轴和y 轴正半轴上的点。
平行四边形动点典型例题平行四边形是一种特殊的四边形，其中对边是平行的。
在平行四边形中，有一些特殊的点和线段，它们有着独特的性质和关系。
动点问题是一类常见的几何问题，其中一个或多个点在空间中移动，我们需要研究它们的位置、关系和性质的变化。
下面，我们来看一个典型的平行四边形动点问题：问题描述：在平行四边形ABCD中，点E是边BC上的一动点，连接AE交边CD于点F。
求证：当点E在边BC上变动时，线段EF的中点一直在直线AC上。
解决方法：我们首先观察到，当点E在边BC上移动时，线段EF的中点一定在线段AF上，因为根据平行四边形的性质，线段AE与线段FC平行且等长。
接下来，我们需要证明线段AF与直线AC重合。
我们可以利用平行四边形的性质和平行线的性质来证明这一点。
首先，根据平行四边形的定义，我们知道线段AD与线段BC是平行的。
又因为线段AE与线段FC平行，所以线段AF与线段DC平行。
因此，线段AF与线段AC是平行的。
接下来，我们需要证明线段AF与线段AC也是等长的。
我们可以使用割线定理来证明这一点。
根据割线定理，当一条割线与两条平行线相交时，它将两条平行线上的交点分成相等的两部分。
在这个问题中，我们可以看到线段AE与线段FC平行，线段AF与线段DC平行，所以根据割线定理，线段AF与线段AC相等。
由于线段AF与线段AC既平行又等长，所以它们重合，即线段EF的中点一直在直线AC上。
通过这个例题，我们可以看到，动点问题可以通过观察和利用几何性质来解决。
平行四边形是几何学中一个重要的概念，在解决动点问题时经常会涉及到。
理解和掌握平行四边形的性质和特点，对于解决动点问题是非常有帮助的。
中考数学压轴题：“动点产生的平行四边形问题”训练及解析先思考三个问题：1．已知A、B、C三点，以A、B、C、D为顶点的平行四边形有几个，怎么画？2．在坐标平面内，如何理解平行四边形ABCD的对边AB与DC平行且相等？3．在坐标平面内，如何理解平行四边形ABCD的对角线互相平分？图1 图2 图3 如图1，过△ABC的每个顶点画对边的平行线，三条直线两两相交，产生三个点D．如图2，已知A(0, 3)，B(－2, 0)，C(3, 1)，如果四边形ABCD是平行四边形，怎样求点D的坐标呢？点B先向右平移2个单位，再向上平移3个单位与点A重合，因为BA与CD平行且相等，所以点C(3, 1) 先向右平移2个单位，再向上平移3个单位得到点D(5, 4)．如图3，如果平行四边形ABCD的对角线交于点G，那么过点G画任意一条直线（一般与坐标轴垂直），点A、C到这条直线的距离相等，点B、D到这条直线的距离相等．关系式x A＋x C＝x B＋x D和y A＋y C＝y B＋y D有时候用起来很方便．我们再来说说压轴题常常要用到的数形结合．如图4，点A是抛物线y＝－x2＋2x＋3在x轴上方的一个动点，AB⊥x轴于点B，线段AB交直线y＝x－1于点C，那么点A的坐标可以表示为(x,－x2＋2x＋3)，点C的坐标可以表示为(x, x－1)，线段AB的长可以用点A的纵坐标表示为AB＝y A＝－x2＋2x＋3，线段AC的长可以用A、C两点的纵坐标图4表示为AC＝y A－y C＝(－x2＋2x＋3)－(x－1)＝－x2＋x＋2．通俗地说，数形结合就是：点在图象上，可以用图象的解析式表示点的坐标，用点的坐标表示点到坐标轴的距离．例 24 2014年湖南省岳阳市中考第24题如图1，抛物线经过A (1, 0)、B (5, 0)、C 10(0,)3三点．设点E (x , y )是抛物线上一动点，且在x 轴下方，四边形OEBF 是以OB 为对角线的平行四边形． （1）求抛物线的解析式；（2）当点E (x , y )运动时，试求平行四边形OEBF的面积S 与x 之间的函数关系式，并求出面积S 的最大值；（3）是否存在这样的点E ，使平行四边形OEBF 为正方形？若存在，求点E 、F 的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“14岳阳24”，拖动点E 运动，可以体验到，当点E 运动到抛物线的顶点时，S 最大．当点E 运动到OB 的垂直平分线上时，四边形OEBF 恰好是正方形． 思路点拨1．平行四边形OEBF 的面积等于△OEB 面积的2倍．2．第（3）题探究正方形OEBF ，先确定点E 在OB 的垂直平分线上，再验证EO ＝EB ． 图文解析（1）因为抛物线与x 轴交于A (1, 0)、B (5, 0)两点，设y ＝a (x －1)(x －5)． 代入点C 10(0,)3，得1053a =．解得23a =． 所以抛物线的解析式为22210(1)(5)4333y x x x x =--=-+． （2）因为S ＝S 平行四边形OEBF ＝2S △OBE ＝OB ·(－y E ) ＝22105(4)33x x --+＝210(65)3x x --+＝21040(3)33x --+． 所以当x ＝3时，S 取得最大值，最大值为403．此时点E 是抛物线的顶点（如图2）． （3）如果平行四边形OEBF 是正方形，那么点E 在OB 的垂直平分线上，且EO ＝EB ． 当x ＝52时，22355(1)(5)()33222y x x =--=⨯⨯-=-．此时E 55(,)22-． 如图3，设EF 与OB 交于点D ，恰好OB ＝2DE ． 所以△OEB 是等腰直角三角形．所以平行四边形OEBF 是正方形．所以当平行四边形OEBF 是正方形时，E 55(,)22-、F 55(,)22．图2 图3考点伸展既然第（3）题正方形OEBF 是存在的，命题人为什么不让探究矩形OEBF 有几个呢？ 如图4，如果平行四边形OEBF 为矩形，那么∠OEB ＝90°．根据EH 2＝HO ·HB ，列方程22(1)(5)(5)3x x x x ⎡⎤---=-⎢⎥⎣⎦． 或者由DE ＝12OB ＝52，根据DE 2＝254，列方程225225()(1)(5)234x x x ⎡⎤-+---=⎢⎥⎣⎦． 这两个方程整理以后都是一元三次方程4x 3－28x 2＋53x －20＝0，这个方程对于初中毕业的水平是不好解的． 事实上，这个方程可以因式分解，51(4)()()022x x x ---=．如图3，x ＝52；如图4，x ＝4；如图5，x ＝12，但此时点E 在x 轴上方了． 这个方程我们也可以用待定系数法解： 设方程的三个根是52、m 、n ，那么4x 3－28x 2＋53x －20＝54()()()2x x m x n ---． 根据恒等式对应项的系数相等，得方程组441028,1010453,1020.m n m n mn mn ++=⎧⎪++=⎨⎪=⎩解得4,1.2m n =⎧⎪⎨=⎪⎩图4 图5例 25 2014年湖南省益阳市中考第20题如图1，直线y＝－3x＋3与x轴、y轴分别交于点A、B，抛物线y＝a(x－2)2＋k经过A、B两点，并与x轴交于另一点C，其顶点为P．（1）求a，k的值；（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求点Q的坐标；（3）在抛物线及其对称轴上分别取点M、N，使以A、C、M、N为顶点的四边形为正方形，求此正方形的边长．】图1动感体验请打开几何画板文件名“14益阳20”，可以体验到，点Q在线段AB的垂直平分线上．还可以体验到，正方形的对角线为AC，有一个顶点恰为抛物线的顶点．思路点拨1．第（2）题的等腰三角形只考虑QA＝QB的情形．2．第（3）题的正方形不可能AC为边，只存在AC为对角线的情形．图文解析（1）由y＝－3x＋3，得A(1, 0)，B(0, 3)．将A(1, 0)、B(0, 3)分别代入y＝a(x－2)2＋k，得0,4 3.a ka k+=⎧⎨+=⎩解得a＝1，k＝－1．（2）如图2，抛物线的对称轴为直线x＝2，设点Q的坐标为(2, m)．已知A(1, 0)、B(0, 3)，根据QA2＝QB2，列方程12＋m2＝22＋(m－3)2．解得m＝2．所以Q(2, 2)．（3）点A(1, 0)关于直线x＝2的对称点为C(3, 0)，AC＝2．如图3，如果AC为正方形的边，那么点M、N都不在抛物线或对称轴上．如图4，当AC为正方形的对角线时，M、N中恰好有一个点是抛物线的顶点(2,－1) ．因为对角线AC＝2．图2 图3 图4考点伸展如果把第（3）题中的正方形改为平行四边形，那么符合条件的点M有几个？①如果AC为对角线，上面的正方形AMCN是符合条件的，M(2,－1)．②如图5，如果AC为边，那么MN//AC，MN＝AC＝2．所以点M的横坐标为4或0．此时点M的坐标为(4, 3)或(0, 3)．第（2）题如果没有限制等腰三角形ABQ的底边，那么符合条件的点Q有几个？①如图2，当QA＝QB时，Q(2, 2)．②如图6，当BQ＝BA B为圆心，BA为半径的圆与直线x＝2有两个交点．m=根据BQ2＝10，列方程22＋(m－3)2＝10，得3此时Q(2,3或(2,3．③如图7，当AQ＝AB时，以A为圆心，AB为半径的圆与直线x＝2有两个交点，但是点(2,－3)与A、B三点共线，所以Q(2, 3)．图5 图6 图7例 26 2014年湖南省邵阳市中考第25题准备一张矩形纸片（如图1），按如图2操作：将△ABE 沿BE 翻折，使点A 落在对角线BD 上的点M ，将△CDF 沿DF 翻折，使点C 落在对角线BD 上的点N ．（1）求证：四边形BFDE 是平行四边形；（2）若四边形BFDE 是菱形，AB ＝2，求菱形BFDE 的面积．图1图2动感体验请打开几何画板文件名“14邵阳25”，拖动点D 可以改变矩形ABCD 的形状，可以体验到，当EM 与FN 在同一条直线上时，四边形BFDE 是菱形，此时矩形的直角被三等分． 思路点拨1．平行四边形的定义和4个判定定理都可以证明四边形BFDE 是平行四边形．2．如果平行四边形BFDE 是菱形，那么对角线平分一组对角，或者对角线互相垂直．用这两个性质都可以解答第（2）题．图文解析（1）如图3，因为AB //DC ，所以∠ABD ＝∠CDB ．又因为∠1＝∠2，∠3＝∠4，所以∠1＝∠3．所以BE //FD ．又因为ED //BF ，所以四边形BFDE 是平行四边形．图3 图4（2）如图4，如果四边形BFDE 是菱形，那么∠1＝∠5．所以∠1＝∠2＝∠5．由于∠ABC ＝90°，所以∠1＝∠2＝∠5＝30°．所以BD ＝2AB ＝4，AE ＝3．所以ME ＝3．所以S 菱形BFDE ＝2S △BDE ＝BD ·ME ＝3．考点伸展第（1）题的解法，我们用平行四边形的定义作为判定的依据，两组对边分别平行的四边形叫平行四边形．还可以这样思考：证明四边形BFDE 的两组对边分别相等；证明ED 与BF 平行且相等；证明四边形BFDE 的两组对角分别相等．这三种证法，都要证明三角形全等，而全等的前提，要证明∠1＝∠2＝∠3＝∠4． 这样其实就走了弯路，因为由∠1＝∠3，直接得到BE //FD ，根据平行四边形的定义来得快．能不能根据BD 与EF 互相平分来证明呢？也是可以的：如图5，设EF 与BD 交于点O ，根据“角角边”证明△EMO ≌△FNO ，得到EF 与MN 互相平分．又因为BM ＝DN ，于是得到EF 与BD 互相平分．图5 图6第（2）题的解法，我们用了菱形的性质：对角线平分每组对角，得到30°的角． 我们也可以根据菱形的对角线互相垂直平分来解题：如图6，如果四边形BFDE 是菱形，那么对角线EF ⊥BD ，此时垂足M 、N 重合． 因此BD ＝2DC ．这样就得到了∠5＝30°．事实上，当四边形BFDE 是菱形时，矩形ABCD 被分割为6个全等的直角三角形．由AB ＝2，得AD ＝ABCD 的面积为菱形面积占矩形面积的23．。
专题03特殊平行四边形中的三种几何动点问题类型一、面积问题例．如图，在四边形ABCD 中，AB CD ∥，90BCD ∠= ，10cm AB AD ==，=8cm BC ．点P 从点A 出发，以每秒3cm 的速度沿折线ABC 方向运动，点Q 从点D 出发，以每秒2cm 的速度沿线段DC 方向向点C 运动．已知动点P ，Q 同时发，当点Q 运动到点C 时，P ，Q 运动停止，设运动时间为t ．(1)直接写出CD 的长（cm ）；(2)当四边形PBQD 为平行四边形时，直接写出四边形PBQD 的周长（cm ）；(3)在点P 、点Q 的运动过程中，是否存在某一时刻，使得BPQ V 的面积为215cm ？若存在，请求出所有满足条件的t 的值；若不存在，请说明理由．【变式训练1】如图，在四边形ABCD 中，,90,120,12cm,15cm AD BC A B ADC AD BC ∠=∠=︒∠=︒==∥，点P 自点A 沿折线AD DC -以1cm/s 的速度运动，点Q 自点C 沿向CB BA -以1cm/s 的速度运动．点P ，Q 同时出发，其中一个点到达终点，另一个点也停止运动．设运动时间为(s)t ．(1)当P 在AD 边上，点Q 在BC 边上时，如图1．①用含t 的代数式表示：DP =___________，BQ =___________；②若四边形APQB 是平行四边形，求t 的值？(2)求BPQ V 的面积S 与运动时间t 之间的数量关系式，并写出t 的取值范围．【变式训练2】如图，在矩形ABCD 中，AB =12，BC =18，点P 从点A 出发，以每秒2个单位长度的速度沿类型二、几何图形存在性问题长的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D E ，运动的时间是t 秒()0t >．过点D 作DF BC ⊥于点F ，连接DE ，EF ．(1)求AB AC ，的长；(2)求证：AE DF =；(3)当t 为何值时，DEF 为直角三角形？请说明理由．例2．如图，已知正方形ABCD 的边长为4cm ，动点P 从点B 出发，以2cm /s 的速度沿B C D →→方向向点D 运动，动点Q 从点A 出发，以1cm /s 的速度沿A B →方向向点B 运动，若P 、Q 两点同时出发运动时间为s t ．(1)连接PD 、PQ 、DQ ，求当t 为何值时，PQD △的面积为27cm ？(2)当点P 在BC 上运动时，是否存在这样的t 使得PQD △是以PD 为一腰的等腰三角形？若存在，请求出符合条件的t 的值；若不存在，请说明理由．例3．如图，在四边形ABCD 中，AD ∥BC ，∠B ＝90°，AB ＝8cm ，AD ＝12cm ，BC ＝18cm ，点P 从点A 出发以1cm/s 的速度向点D 运动；点Q 从点C 同时出发，以2cm/s 的速度向点B 运动，当点Q 到达点B 时，(1)填空：AB =；菱形ABCD 的面积S =；菱形的高h =．(2)若点M 的速度为每秒1个单位，点N 的速度为每秒a 个单位（其中52a <），当4t =时在平面内存在点得以A ，M ，N ，E 为顶点的四边形为菱形，请求出所有满足条件的a 的值．类型三、直线位置关系问题例1．如图，在Rt ABC △中，90ABC ∠=︒，5AC =，4BC =，点D 是边AB 的中点，动点P 从点A 出发(1)直接写出AB的长．(2)当点Q落在AB边上时，用含t的代数式表示(1)分别求BD和BE的长度；(2)连接PQ，当95t=时，判断PQ与AD是否垂直，并说明理由；(3)试判断是否存在t的值，使得以P，Q，C，DC 点以1cm /s 的速度运动，动点Q 从点B 开始沿BA 向A 点以3cm /s 的速度运动，P ，Q 分别从点D ，B 同时出发，当其中一点到达终点时，另一点也随之停止运动，运动的时间为t 秒．(1)t 为何值时，四边形DPQA 为矩形？(2)t 为何值时，四边形PQBC 为平行四边形？2．如图，在ABC 中，6cm AC =，=8cm BC ，点O 以每秒1cm 的速度由点A 向点C 运动(不与点C 重合)，过点O 作直线MN BC ∥，BCA ∠的外角平分线CF 于点F ，ACB ∠的平分线CE 于点.E 设运动时间为t 秒．发现：(1)在点O 的运动过程中，OE 与OF 的关系是______，请写出理由．(2)当=2t 时，=EF ______cm ．探究：当=t ______时，四边形AECF 是矩形，并证明你的结论．拓展：若点O 在运动过程中，能使四边形AECF 是正方形，试写出线段AB 的长度．(直接写出结论即可)3．已知正方形ABCD 中，8AB BC CD DA ====，90A B C D ∠=∠=∠=∠=︒．动点P 以每秒2个单位速度从点B 出发沿线段BC 方向运动，动点Q 同时以每秒8个单位速度从B 点出发沿正方形的边(1)当运动时间为秒时，点P与点Q相遇；∥时，求线段DQ的长度；(2)当BQ PD全等时，求t的值．(3)连接PA，当PAB和QAD(1)CB的长为______．(2)用含t的代数式表示线段QB的长．(3)连接PQ，=；(1)求证：PE DQ(1)=a______cm，b=______cm；(2)t为何值时，EP把四边形BCDE的周长平分？(1)当2t =时，BP =___________cm ；(2)当t 为何值时，连接,,CP DP CDP △是等腰三角形；(3)Q 为AD 边上的点，且6DQ =，P 与Q 不重合，当t 为何值时，以长方形的两个顶点及点P 为顶点的三角形与DCQ 全等．。
