电路实验报告互易定理

数字逻辑实验互易定理数字逻辑实验：互易定理引言：在数字逻辑领域中，互易定理是一种重要的定理，它在逻辑电路设计和分析中起到了至关重要的作用。

本篇文章将从互易定理的定义、推导过程、应用以及实验方法等方面进行详细介绍。

一、互易定理的定义：互易定理，又称为De Morgan定理，是描述与逻辑运算有关的两个重要等价关系。

在逻辑电路设计和分析中，互易定理可以将逻辑门的输入和输出之间的关系进行转换。

根据互易定理，可以通过将逻辑门的输入和输出之间的关系进行逆转，从而简化电路的设计和分析过程。

二、互易定理的推导过程：互易定理的推导过程主要基于布尔代数的运算规则，以下是互易定理的两种形式及其推导过程：第一种形式：互补定理（Complement Theorem）： A + A’ = 1推导过程如下：A + A’ = (A + A’) · 1 （乘以1不改变其值）= (A + A’) · (A + A’)’（A’ = (A + A’)‘）= A + A’· A’（分配律）= A + 0 （A’· A’ = 0）= A （A + 0 = A）第二种形式：互补定理（Complement Theorem）： A · A’ = 0推导过程如下：A · A’ = (A · A’) + 0 （加0不改变其值）= (A · A’) + (A · A’)’（A’ = (A · A’)‘）= A · (A’ + A’)’（分配律）= A · 1’（A’ + A’ = 1）= A · 0 （1’ = 0）= 0 （A · 0 = 0）三、互易定理的应用：互易定理在逻辑电路设计和分析中有着广泛的应用。

以下是互易定理常见的应用场景：逻辑门电路的简化：互易定理可以用于简化逻辑门电路。

通过将逻辑门的输入和输出之间的关系进行逆转，可以减少逻辑门的数量和复杂度，从而降低电路的成本和功耗。

数字逻辑实验互易定理互易定理是数字逻辑中的一个重要理论，这是一个关于逻辑代数中可以交换、分配和结合性的定理，可以帮助我们简化逻辑电路复杂性和分析数字信号的性质。

在以下文章中，我们将讨论互易定理的概念和其在数字逻辑电路设计中的应用。

1. 什么是互易定理？互易定理是数字逻辑中应用最广泛的定理之一，也是布尔代数的基本定理。

它指的是在保持逻辑等价的前提下，两个变量之间的逻辑运算可以互相交换。

具体来说，互易定理可以简单地表达为交换输入和输出的顺序不会改变一个逻辑函数的输出。

互易定理可以分为以下几种：(1) 交换律：两个量的顺序可以交换而不会改变结论。

A∧B=B∧A， A∨B=B∨A(2) 结合律：在运算规则下，三个或多个量的连锁顺序可以随意连锁。

(A∧B)∧C=A∧(B∧C)，(A∨B)∨C=A∨(B∨C)(3) 分配律：对于两个输入变量，逻辑运算可以分配，而不影响逻辑等价性。

A∧(B∨C)=(A∧B)∨(A∧C)，A∨(B∧C)=(A∨B)∧(A∨C)2. 互易定理的应用数字逻辑电路设计中的互易定理是一个非常重要且必须掌握的概念。

它对于简化逻辑运算和减少逻辑门的数量至关重要。

下面我们将详细讨论几种使用互易定理简化逻辑表达式的情况。

(1) 使用交换律简化交换律非常适合于逻辑电路设计中的代数式和布尔函数的化简。

在这个例子中，我们可以看到，一个变量的顺序被交换，这就使它们可以互相交换，而不会改变逻辑函数的结果。

例如，有以下两个逻辑表达式：A∧B∧C∧DD∧C∧B∧A很明显，这两个表达式的逻辑运算结果相同。

通过交换律，我们可以互换变量次序并得到相同的结果，这在设计数字逻辑电路时非常有用。

(2) 使用结合律简化在电路设计中，我们有时需要找到一种方法来简化逻辑运算，使其更容易维护和理解。

通过使用结合律，我们可以将多个变量进行组合，使其更易于计算。

例如，有以下两个逻辑表达式：(A∧B)∧CA∧(B∧C)对于这两个逻辑表达式，使用结合律可以得到更为简单的表达式。

特勒根定理设有电路,A B ，满足：（1）两者的拓扑图完全相同，均有n 个节点b 条支路；（2）对应的支路和节点均采用相同的编号，其中B 电路的电流、电压加“^”号；（3）各支路电流、电压参考方向均取为一致，则有： 功率守恒定理：01bU I k k k =∑=ˆˆ01bU I k kk =∑= 似功率守恒定理：ˆ01bU I k k k =∑= 1ˆ0b k k k U I ==∑适用于各种电路：直流、交流；线性、非线性；被称为基尔霍夫第三定律。

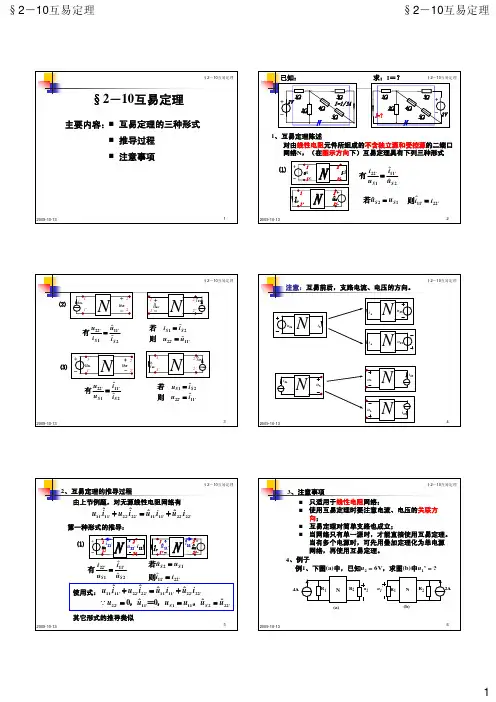
§2－2互易定理在线性电路中，若只有一个独立电源作用，网络只含有线性电阻（不含受控源），则在一定的激励与响应的定义下，二者的位置互易后，响应与激励的比值不变。

互易定理的证明需要特勒根定理（或二端网络等效的概念）。

根据激励和响应是电压还是电流，互易定理有三种形式：1、互易定理的第一种形式S uS u ˆ+-电路在方框内仅含线性电阻，不含任何独立电源和受控源。

电压源s u 接在端子1-1'，支路2-2'短路，其电流为2i 。

如果把激励和响应位置互换，此时ˆs u接于2-2'，而响应则是接于1-1'，短路电流1ˆi。

21ˆˆs s i i u u=，若 ˆs s u u =，则21ˆi i =。

对一个仅含线性电阻的电路，在单一电压源激励而响应为电流时，激励和响应互换位置，不改变同一激励产生的响应。

2、互易定理的第二种形式2'1i +-22u 1'1Si2'Si ˆ+-21ˆu 1'12ˆi21ˆˆs s u u i i= 若ˆs s i i=，则21ˆu u =。

3 互易定理的第三种形式2'1i 2S i 2i 1'12'S u ˆ+-2ˆi 21ˆu1'1+-21ˆˆs s i u i u= 若数值上ˆs s i u =，则数值上21ˆi u =。

实验七叠加定理和互易定理
一、实验目的
加深对互易定理的内容的理解。

二、原理与说明
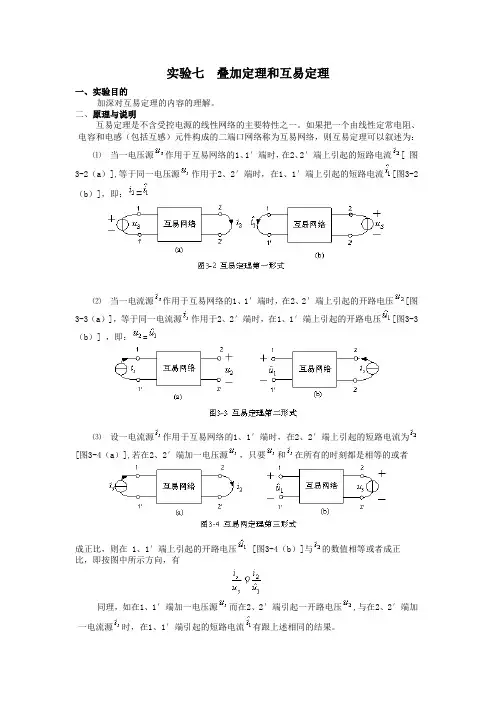
互易定理是不含受控电源的线性网络的主要特性之一。

如果把一个由线性定常电阻、电容和电感（包括互感）元件构成的二端口网络称为互易网络，则互易定理可以叙述为：
⑴ 当一电压源作用于互易网络的1、1′端时，在2、2′端上引起的短路电流[ 图3-2（a）],等于同一电压源作用于2、2′端时，在1、1′端上引起的短路电流[图3-2（b）]，即：=
⑵ 当一电流源作用于互易网络的1、1′端时，在2、2′端上引起的开路电压[图3-3（a）]，等于同一电流源作用于2、2′端时，在1、1′端上引起的开路电压[图3-3（b）] ，即：=
⑶ 设一电流源作用于互易网络的1、1′端时，在2、2′端上引起的短路电流为[图3-4（a）],若在2、2′端加一电压源，只要和在所有的时刻都是相等的或者
成正比，则在 1、1′端上引起的开路电压 [图3-4（b）]与的数值相等或者成正
比，即按图中所示方向，有
同理，如在1、1′端加一电压源而在2、2′端引起一开路电压,与在2、2′端加一电流源时，在1、1′端引起的短路电流有跟上述相同的结果。

三、实验内容及步骤
验证互易定理
表7-1
U S!=25V U S@=20V
I2(mA)
I1(mA)
表7-2
I1=10mA I2=15mA
I2(mA)
I1(mA)
表7-3
I1=10mA U2=10V
I2(m A)。

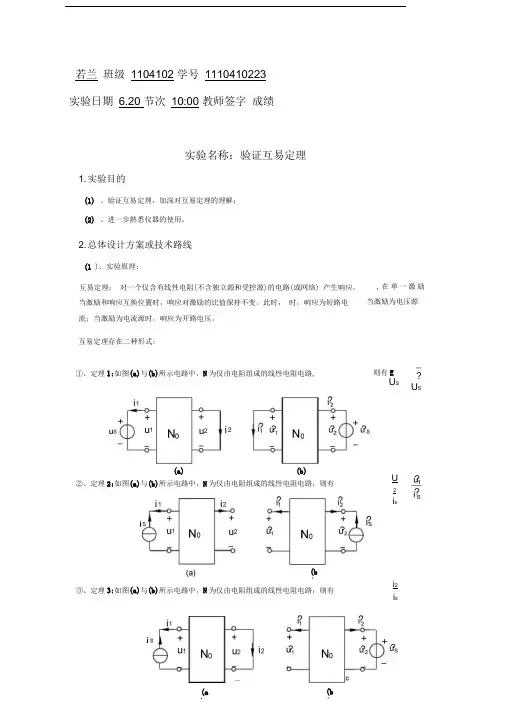
①、定理1:如图(a)与(b)所示电路中，N为仅由电阻组成的线性电阻电路, 则有EU S_?U S(a) (b)②、定理2:如图(a)与(b)所示电路中，N为仅由电阻组成的线性电阻电路，则有③、定理3:如图(a)与(b)所示电路中，N为仅由电阻组成的线性电阻电路，则有若兰班级1104102 学号1110410223实验日期 6.20 节次10:00 教师签字成绩实验名称：验证互易定理1. 实验目的(1)、验证互易定理，加深对互易定理的理解；(2)、进一步熟悉仪器的使用。

2. 总体设计方案或技术路线(1 )、实验原理:互易定理：对一个仅含有线性电阻(不含独立源和受控源)的电路(或网络) 产生响应，当激励和响应互换位置时，响应对激励的比值保持不变。

此时，时，响应为短路电流；当激励为电流源时，响应为开路电压。

互易定理存在二种形式:,在单一激励当激励为电压源(b)U2i si2i s(2)、实验方案i 1;电路图一，证明| 2=u〔；电路图二，证明L2=U S=i 1/1 S电路图三，证明L2/(电路图如下)3. 实验电路图各参数分别为：Rl = R3=Rl=R5=100 Q R2=200Q L S=6V I S=50mA 4. 仪器设备名称、型号交直流电路实验箱一台直流电压源0〜30V 一台直流电流源0〜100mA 一台直流电流表0〜400mA 一只数字万用表一只电阻若干5. 理论分析或仿真分析结果6. 详细实验步骤及实验结果数据记录（包括各仪器、仪表量程及阻的记录）（1）、验证定理一，按照图一连好电路后测量12、i 1,将实验数据记录在表格i中;U i将实验数据记录在表格2中; （2）、验证定理二，按照图二连好电路后测量L2i i,将实验数据记录在表格3中。

（3）、验证定理三，按照图三连好电路后测量L27. 实验结论8. 实验中出现的问题及解决对策(1)、问题：实验过程中无200 Q定值电阻；对策：改成两个100Q定值电阻串联；(2)、问题：实验中电流表无示数，后经检查电路发现该实验台电流表被烧坏，对策：换了一台没有问题的直流电流表。

实验2 叠加定理和互易定理的验证
实验目的：
1.验证叠加定理
实验原理：
1.叠加定理：在线性系统中，若输入信号可以分解成多个不同的分量，每个分量独立地经过系统后再将输出信号叠加（相加），那么这个输出信号与将这些分量分别输入系统后输出信号的叠加结果是完全相同的。

即，系统是可叠加的。

2.互易定理：互易定理是指对于某一系统，若输入为x(t)，输出为y(t)，那么输入为x*(-t)时输出为y*(-t)。

其中，x*(-t)是x(t)的共轭反转。

互易定理要求系统具有逆时不变性和线性性。

实验步骤：
1.搭建实验仪器，如图所示，系统输入为三角波和正弦波，系统输出为观测波形。

2.分别观察三角波和正弦波在系统中的输出波形，记录。

3.将三角波和正弦波分别分解成三个谐波分量，分别经过系统，分别观测三个分量的输出波形，并将三个分量的输出波形叠加，记录。

实验结果：
3.将三角波和正弦波的共轭反转输入系统，观测输出波形，如下图所示，其中绿色为三角波输出波形，蓝色为正弦波输出波形。

1.通过观察三角波和正弦波在系统中的输出波形，可以发现系统具有线性性和时不变性，符合叠加定理和互易定理的要求。

3.通过将三角波和正弦波的共轭反转输入系统，观测输出波形，可以验证互易定理的正确性，可以发现输入信号的共轭反转与输出信号的共轭反转呈镜像关系。

互易定理中国大学M O O C中国大学M OO C中国大学M O OC中国大学M O OC中国大学MO O C中国大学M O O C互易定理仅适用于一个仅含线性电阻，且只有一个激励的电路，在保持电路将独立电源置零后电路拓扑结构不变的条件下，激励与响应互换位置后，响应和激励的比值保持不变。

一个具有互易性的网络在输入端（激励）与输出端（响应）互换位置后，同一激励所产生的响应并不改变。

具有互易性的网络叫互易网络，互易定理是对电路的这种性质所进行的概括，它广泛地应用于网络的灵敏度分析和测量技术等方面。

中国大学MOOC中国大学MOOC中国大学M O OC 国大学MOOC中国大学MOOC中国大学M OO C中国大学MOOC中国大学MOOC中国大学MO OC国大学MOOC中国大学MOOC中国大学MO OC中国大学MO O C中国大学MOOC中国大学MO OC中国大学M O O C 中国大学M O O C中国大学M O O C激励电压源电流(短路)响应当时，则两个支路中电压电流有如下关系：）a （dcba2i 1S u _+RN 络网阻电性线）b （dcba_+RN 络网阻电性线 1.互易定理的第一种形式或==∧∧i u i uu iu i ˆ ˆ2S11S2S11S22）c （dc ba RN u S1=u ∧S2i 1=i 2中国大学M O O C 中国大学M O O C 中国大学M O O C国大学M O OC中国大学MO O C 中国大学MOO C中国大学M O O C中国大学MOO C中国大学MO OC国大学M OO C中国大学MO OC中国大学MO OC中国大学M OO C中国大学MOOC中国大学MO OC中国大学M O O C中国大学M O O C 中国大学M OO C2S ˆu1ˆi将图(a)与图(b)中支路1、2的条件代入，即:即：证毕！或==∧∧i u i uu i u iˆ ˆ2S11S2S11S22+⨯=⨯+∧u ii i u i S1121S22ˆ0ˆ 0 ∧∧====u u u u u u 1S1212S2, 0 , 0,）a （dc ba 2i 1S u _+RN 络网阻电性线）b （dcb a_+RN 络网阻电性线证明:中国大学MOOC中国大学MOOC中国大学MO O C 国大学MOOC 中国大学MOOC中国大学M OO C中国大学MOOC中国大学MOOC中国大学MOOC国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOO C中国大学MOOC2S ˆu1ˆi激励电流源电压(开路)响应则两个支路中电压电流有如下关系：当时，）a （dcba 1S i 2u _+RN 络网阻电性线）b （dcba_+RN 网络电阻线性2.互易定理的第二种形式或u i u iu i u i ==∧∧∧∧ 2S11S21S12S2）c （dcbaRN i S1=i ∧S2u ∧1=u 2中国大学M O O C 中国大学M O O C 中国大学M O O C国大学M OOC中国大学M OO C 中国大学M OO C中国大学M O O C中国大学MO OC中国大学MO OC国大学M O OC 中国大学MOO C中国大学MO OC中国大学M O OC中国大学M O OC中国大学MO OC中国大学M OO C 中国大学M O O C 中国大学M OO C1ˆu2S ˆi证明:由特勒根定理：+=+∧∧u i u i u i u i 11221122ˆˆ∧∧=−===−i i i i i i 1S1212S2, 0 , 0,1i ）a （d cba 1S i 2u _+RN 络网阻电性线⨯−=−+⨯∧∧u u i u i u 0 0 12S2S112=∧∧u i u i 2S21S1或u i u iu i u i ==∧∧∧∧ 2S11S21S12S2dcba_+RN 络网阻电性线中国大学MOOC中国大学MOOC中国大学MO O C 国大学MOOC中国大学MOOC中国大学MOOC中国大学MOOC中国大学MOOC中国大学MO OC国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MO O C中国大学MOOC1ˆu2S ˆi2ˆi则两个支路中电压电流在数值上有如下关系：当时，激励电流源电压源图b图a电流响应图b图a电压1i 2i ）a （dc ba 1S i RN 络网阻电性线_+）b （dcba_+RN 络网阻电性线3.互易定理的第三种形式或==∧∧∧∧i i u uu i u i 2S11S21S1S22）c （dcb a RN u ∧1=i 2i S1=u ∧S2中国大学MOOC中国大学MOOC中国大学MO OC国大学MOOC中国大学MOOC中国大学MOOC 中国大学MOOC中国大学MOOC中国大学MO OC国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOOC中国大学MOO C1ˆu2S ˆu证明:由特勒根定理：+=+∧∧u i u i u i u i 11221122ˆˆi i u i u u =−===∧∧∧1S1212S2, 0 , 0,⨯+⨯=+∧∧u iu i u i 121S1S2200ˆ - =∧∧u i u i 1S1S22或==∧∧∧∧i i u uu i u i 2S11S21S1S22_+dcba_+RN 络网阻电性线1i 2i ）a （dcba 1S i RN 络网阻电性线中国大学MOOC中国大学MOOC中国大学MO O C 国大学MOOC中国大学MOOC中国大学M OOC中国大学MOOC中国大学MOOC中国大学MO OC国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOOC中国大学MO OC中国大学MOOC中国大学MOOC中国大学MOOC1ˆu2S ˆu(3)互易定理只适用于线性电阻网络在单一电源激励下，两个支路电压电流关系。

实验名称：互易定理的验证
一实验目的
1.验证互易定理三种形式的正确性
2.加深对互易定理的认识和理解
二实验设备
2个直流稳压源（0—30V可调）
1个直流数字电压表（0—200Ｖ）
１个直流数字毫安表（0—200mＡ）
叠加原理实验电路板
导线若干
三实验原理
互易定理：对于一个仅含二端线性电阻的电路，在单一激励的情况下，当激励和响应互换位置时，将不改变同一激励所产生的响应
1.互易定理形式一.
2.互易定理形式二
3.互易定理形式三
四实验方案与步骤
1.按图一连接电路，令，测出和，并记录
2.按图二连接电路，令，测出和，并记录
1.按图三连接电路，令，测出和，并记录
五实验结果与数据处理
对比每组实验的两个数据，在实验误差允许的范围内，，即验证了互易定理。

一、实验目的1. 验证互易原理在电路中的应用。

2. 理解互易原理的基本概念及其在电路分析中的重要性。

3. 掌握通过实验方法验证互易原理的步骤和技巧。

二、实验原理互易原理是指在线性、无源和可逆的电路中，当某一电源或信号源施加在电路的某一部分时，电路的响应与将该电源或信号源移至电路的另一部分时产生的响应相同。

具体来说，对于线性电路，如果电路中某一支路的电流或电压是某一独立源单独作用时在该支路所产生的电流或电压的代数和，那么这个电路就满足叠加原理；如果电路中某一支路的电流或电压与另一支路的电压或电流存在一定的关系，那么这个电路就满足互易定理。

三、实验设备1. 直流稳压电源（双路0～30V可调）1台；2. 直流电压表、直流电流表各1块；3. EEL53单元板1块；4. 低压导线若干。

四、实验内容本实验采用EEL53单元板搭建一个简单的电路，通过实验验证互易原理。

1. 搭建电路：根据实验原理，搭建如图1所示的电路，其中US1为恒压源，US2为恒流源，开关S1和S2用于控制电路的连接。

2. 实验步骤：（1）将开关S1拨向上边，开关S2投向下边短路侧，将直流电压表接在US1的输出端，测量US1的输出电压U1。

（2）将直流电流表接在US2的输出端，测量US2的输出电流I2。

（3）将开关S1拨向下边，开关S2投向上边，将直流电压表接在US2的输出端，测量US2的输出电压U2。

（4）将直流电流表接在US1的输出端，测量US1的输出电流I1。

3. 数据处理：（1）记录实验数据，包括U1、I2、U2和I1。

（2）根据实验数据，验证互易原理在电路中的应用。

五、实验结果与分析1. 实验数据：| 测量项目 | 测量值 || -------- | ------ || U1 | 12V || I2 | 2A || U2 | 6V || I1 | 1.5A |2. 结果分析：（1）根据实验数据，可以发现U1=12V，U2=6V，I1=1.5A，I2=2A。

电阻电路实验报告实验目的：1验证叠加定理2验证互易定理形式一3探究最大功率传输条件4电流源与电压源的等效替换5双口网络的短接电导6电阻电路的分压7电阻电路的分流8通过欧姆定律测量电源内阻9探究二极管的性质10kcl的性质实验原理1叠加定理：叠加定理适用于线性电路，当某一独立电源单独作用时，其他独立电源不作用，即置零值。

电压源置零值，用短路线代替；电流源置零值，用开路线代替。

如图当us单独促进作用，电路例如图2右图，由图可以得uo`=r4/(r4+r2)*us当is单独促进作用，电路例如图3右图，由图可以得uo``=r2*r4/(r2+r4)*is由叠加定理得uo=u`+u``由此验证。

2验证互易定理形式一：如图所示的网络nr为仅由线性二端电阻共同组成的网络，当一单一制电压源促进作用于端口1时，在端口2产生的短路电流等同于该单一制电压源移往端口2促进作用时，在端口1产生的短路电流，即i1`=i2。

将互易前图一的端口条件u1=u2,u2=0和互易后图二的端口条件u1`=0,u2`=us代入式即可得证。

探究最小功率传输条件：假定理想电压源和一固定电阻r1，将其视为一个电压源，r1为其内电阻，串联一可变电阻rc，不断改变电阻rc，流过电阻rc的电流不断改变，并分别记录下来，最后通过电流和电阻以及额定电压，来判断最大功率传输的条件。

电路图如下图4电流源与电压源的耦合替代：将一理想电压源与一个固定电阻ro串联可以看作是一个电压源，ro可以看作是内阻，如果将莫一数值的电流源与ro并联在一起，也可以产生原来电压源的效果，这就是电流源与电压源的等效替换，实验原理如图所示先预设一个us的值，将可变电阻调整一固定值，记录电流数值，然后按图二发生改变电路，观测电流表数值，并调节电流源，如果电流表读书合乎之前记录的，就表明电流源与电压源耦合替代。

5双口网络的短路电导参数通过如下图，探究双口网络的电导参数，假设端口电压u1和u2为自变量，而端口电流i1和i2为因变量，这刚好与开路电阻参数情况构成对偶，把端口电压u1和u2看做两个单一制的电压源，如图所示，根据叠加定理和齐次定理得i1=g11u1+g12u2i2=g21u1+g22u2可以获得电导参数g.6电阻电路的分压探究电阻电路分后甩条件，在电源电压额定的时候，各个电阻分后甩情况和各个电阻阻值的比值成正比，也就是说，电阻越大，适当分摊的电压也就越多，检验该定理，采用下面的电路图。