第四章 不完全信息静态博弈-贝叶斯纳什均衡(博弈论与信息经济学-中科院, 张玲玲)
- 格式：ppt
- 大小：494.00 KB
- 文档页数：40
下载文档原格式
合集下载
非合作博弈经济管理学及财务知识分析理论
(7,0) (5,-1) (9,0) (5,-1) (9,0) (5,-1) (9,0)
市场进入博弈-2阶段不完全信息动态博弈
基本思路-不完全信息动态博弈
在静态贝叶斯均衡中，参与人的信念是事前给定的，均衡 概念没有规定参与人如何修正自己的信念。但是，如果进 入者可以任意修订自己有关在位者成本函数的信念，上述 不完全信息动态博弈可以有任意均衡。
假定参与人的类型是独立分布的，参与人i有K个类型， 有h个可能的行动，өk和ah分别代表一个特定的类型和 一个特定的行动。
如果我们观察到i选择了ah，i属于өk的后验概率是多少？
p(ahk)p(k) p(ahk)p(k)
Por{b kah}
(7,0) (5,-1) (9,0) (5,-1) (9,0) (5,-1) (9,0)
市场进入博弈-2阶段不完全信息动态博弈
基本思路-不完全信息动态博弈
精练贝叶斯均衡是贝叶斯均衡、子博弈精练均 衡和贝叶斯推断的结合。它要求：
✓ 1、在每个信息集上，决策者必须有一个定义 在属于该信息集的所有决策结上的一个概率分 布（信念）；
第二个弟子……
第三个弟子……
贝叶斯法则
在日常生活中，当面临不确定时，我们对某事 件发生的可能性有一个判断，然后，会根据新 的信息来修正这个判断。
✓ 统计学上，修正之前的判断称为“先验概率”
✓ 修正后的判断称为“后验概率”
贝叶斯法则就是人们根据新的信息从先验概率 得到后验概率的基本方法。
贝叶斯法则
基本思路-不完全信息动态博弈
成语故事：黔之驴-驴虎博弈
老虎通过不断试探来修正对毛驴的看法， 每一步行动都是给定它的信念下最优的， 毛驴也是如此。最终老虎将毛驴吃掉。
博弈论与信息经济学讲义9-1
பைடு நூலகம்
投保人知道自己的风险，保险公司不知 道；因此保险公司针对不同类型的潜在投 保人制定了不同的保险合同，投保人根据 自己的风险特征选择一个保险合同。
代理人： 委托人： 投保人 保险公司
二 信息经济学的基本分类
非对称信息发生的内容 非 对 称 信 息 发 生 的 时 间
隐藏行动 事 前 隐藏信息 3、逆向选择模型 4、信号传递模型 5、信息甄别模型 2、隐藏信息的道德风 险模型
第六章 委托-代理理论（I）
一 博弈论与信息经济学 二 信息经济学的分类 三 委托-代理理论的分析思路和框架 四 对称信息下的最优合同
委托-代理理论
高
某些可 观测的
签约时信息是对称的
选择行动 接受 提供合同 努力或不 努力
自然
低
结果
代理人 委托人 代理人 不接受
代理人：代理人的行动和自然状态一起决定 某些可观测的结果。 委托人：不能观测到代理人行动本身和自然本身，只能观测到结果。 委托人的问题是：设计一个激励合同以诱使代理人从自身利益出发 选择对委托人最有利的行动。
愿意出高价，这样持有好车的买主只好退出市场，市场上都剩下“坏 车”，买主则越来越不愿意光顾，旧车市场萎缩直至消失。
斯宾斯：人才市场上，由于信息不对称，雇主愿意开出的是较低的工资，
除了平庸的“柠檬”外根本不能满足精英人才的需要。出现了劣币驱逐 良币的现象。
斯蒂格利茨：信贷市场上，由于信息不对称，贷款人只好确定一个较
二 信息经济学的基本分类
信息经济学：从本质上讲，信息经济学 是非对称信息博弈论在经济学上的应用。
二 信息经济学的基本分类
委托人 代理人
博弈中不拥有私人信息的参 与人 交易中没有信息优势的一方
投保人知道自己的风险，保险公司不知 道；因此保险公司针对不同类型的潜在投 保人制定了不同的保险合同，投保人根据 自己的风险特征选择一个保险合同。
代理人： 委托人： 投保人 保险公司
二 信息经济学的基本分类
非对称信息发生的内容 非 对 称 信 息 发 生 的 时 间
隐藏行动 事 前 隐藏信息 3、逆向选择模型 4、信号传递模型 5、信息甄别模型 2、隐藏信息的道德风 险模型
第六章 委托-代理理论（I）
一 博弈论与信息经济学 二 信息经济学的分类 三 委托-代理理论的分析思路和框架 四 对称信息下的最优合同
委托-代理理论
高
某些可 观测的
签约时信息是对称的
选择行动 接受 提供合同 努力或不 努力
自然
低
结果
代理人 委托人 代理人 不接受
代理人：代理人的行动和自然状态一起决定 某些可观测的结果。 委托人：不能观测到代理人行动本身和自然本身，只能观测到结果。 委托人的问题是：设计一个激励合同以诱使代理人从自身利益出发 选择对委托人最有利的行动。
愿意出高价，这样持有好车的买主只好退出市场，市场上都剩下“坏 车”，买主则越来越不愿意光顾，旧车市场萎缩直至消失。
斯宾斯：人才市场上，由于信息不对称，雇主愿意开出的是较低的工资，
除了平庸的“柠檬”外根本不能满足精英人才的需要。出现了劣币驱逐 良币的现象。
斯蒂格利茨：信贷市场上，由于信息不对称，贷款人只好确定一个较
二 信息经济学的基本分类
信息经济学：从本质上讲，信息经济学 是非对称信息博弈论在经济学上的应用。
二 信息经济学的基本分类
委托人 代理人
博弈中不拥有私人信息的参 与人 交易中没有信息优势的一方
不完全信息静态博弈-贝叶斯纳什均衡(博弈论与信息经济学-中科院张玲玲)
类似上述情况称为不完全信息博弈，即在不完 全信息博弈中，至少有一个参与人不知道其他 参与人的支付函数。
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈 海萨尼转换 不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例 三 贝叶斯纳什均衡与混合战略均衡 四 机制设计理论与显示原理
海萨尼转换
被求爱者对于
求爱者的品德的 信息是不完全的。
不完全信息博弈
你 接受 不接受
求爱博弈：
求爱 100，100 -50，0
品德优良者求爱 求爱者 不求爱 0，0
0，0
100x+（-100）（1-x）=0
当x大于1/2时，接受求爱
求爱博弈： 品德恶劣者求爱 求爱者
你 接受 不接受
求爱 100，-100 -50，0
不完全信息博弈
在生活中我们也会碰到这样的问题，比 如一个乞丐向你乞讨，你愿意帮助别人， 但不知道他是真的乞丐还是骗子，该如 何决定呢？如果你喜欢与人为善，你可 能愿意冒一点上当的危险，这不等于你 愚蠢，而是你认为，帮助一个困境中的 人比回绝一个骗子更重要。
不完全信息博弈
不完全信息：每一个参与人对所有其他参与人 的（对手）的特征、战略空间及支付函数有准 确的 知识，否则为不完全信息。
众官听得这个消息，尽皆失色。孔明登城 望之，果然尘土冲天，魏兵分两路杀来。
孔明令众将旌旗尽皆藏匿，打开城门，每 一门用20军士，扮作百姓，洒扫街道。而孔明 羽扇纶巾，引二小童携琴一张，于城上敌楼前 凭栏而望，焚香操琴。
不完全信息博弈
司马懿自马上远远望之，见诸葛亮神态自 若，顿时心生疑忌，犹豫再三，难下决断。又 接到远山中可能有埋伏的情报，于是叫后军做 前军，前军做后军，急速退去。司马懿之子司 马昭问：“莫非诸葛亮无军，故做此态，父何 故便退兵？”
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈 海萨尼转换 不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例 三 贝叶斯纳什均衡与混合战略均衡 四 机制设计理论与显示原理
海萨尼转换
被求爱者对于
求爱者的品德的 信息是不完全的。
不完全信息博弈
你 接受 不接受
求爱博弈：
求爱 100，100 -50，0
品德优良者求爱 求爱者 不求爱 0，0
0，0
100x+（-100）（1-x）=0
当x大于1/2时，接受求爱
求爱博弈： 品德恶劣者求爱 求爱者
你 接受 不接受
求爱 100，-100 -50，0
不完全信息博弈
在生活中我们也会碰到这样的问题，比 如一个乞丐向你乞讨，你愿意帮助别人， 但不知道他是真的乞丐还是骗子，该如 何决定呢？如果你喜欢与人为善，你可 能愿意冒一点上当的危险，这不等于你 愚蠢，而是你认为，帮助一个困境中的 人比回绝一个骗子更重要。
不完全信息博弈
不完全信息：每一个参与人对所有其他参与人 的（对手）的特征、战略空间及支付函数有准 确的 知识，否则为不完全信息。
众官听得这个消息，尽皆失色。孔明登城 望之，果然尘土冲天，魏兵分两路杀来。
孔明令众将旌旗尽皆藏匿，打开城门，每 一门用20军士，扮作百姓，洒扫街道。而孔明 羽扇纶巾，引二小童携琴一张，于城上敌楼前 凭栏而望，焚香操琴。
不完全信息博弈
司马懿自马上远远望之，见诸葛亮神态自 若，顿时心生疑忌，犹豫再三，难下决断。又 接到远山中可能有埋伏的情报，于是叫后军做 前军，前军做后军，急速退去。司马懿之子司 马昭问：“莫非诸葛亮无军，故做此态，父何 故便退兵？”
博弈论与信息经济学-中国科学院研究生院管理学院张玲玲
第一章 概述-人生处处皆博弈
注意两点： 1、是两个或两个以上参与者之间的对策论 当鲁滨逊遇到了“星期五”
石匠的决策与拳击手的决策的区别
第一章 概述-人生处处皆博弈
2、理性人假设 理性人是指一个很好定义的偏好，在面临定的约束条 件下最大化自己的偏好。 博弈论说起来有些绕嘴，但理解起来很好理解， 那就是每个对弈者在决定采取哪种行动时，不但要根 据自身的利益的利益和目的行事，而且要考虑到他的 决策行为对其他人可能的影响，通过选择最佳行动计 划，来寻求收益或效用的最大化。
博弈论与信息经济学
（Game Theory and Information Economics )
张玲玲
中国科学院研究生院管理学院 zhangll@
前言
本课程的教学安排 本课程的主要内容 博弈论概述 本课程的教学目的
讲课及考核方式
学科属性：公共选修课 学时/学分：30/1 预修课程：微观经济学
行动 有先后 对手特征、 支付函数、 战略空间 未知
主要内容简介
第一章 概述-人生处处皆博弈
第一篇 非合作博弈理论
第二章 第三章 第四章 第五章
完全信息静态信息博弈-纳什均衡 完全信息动态搏弈-子博弈精炼纳什均衡 不完全信息静态博弈-贝叶斯纳什均衡 不完全信息动态博弈-精练贝叶斯纳什均衡
囚徒困境
第一章 概述-人生处处皆博弈-囚徒困境
案例1-囚徒困境-纳什均衡
囚徒A
坦白
囚徒
-8大于-10 0大于-1
抵赖
-10，0
-1，-1
（坦白，坦白）是纳什均衡
第一章 概述-人生处处皆博弈-囚徒困境
设定： （1）每个局中人都知道博弈规则和博弈结 果的支付矩阵； （2）每个局中人都是理性的（个人理性和 个人最优决策）； （3）不能“串通”
第四章 不完全信息静态博弈-贝叶斯纳什均衡(博弈论与信息经济学-中科院, 张玲玲)
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈
海萨尼转换
不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例
三 贝叶斯纳什均衡与混合战略均衡
四 机制设计理论与显示原理
不完全信息库诺特模型
企业1
企业2
海萨尼转换
设θi表示参与人i的一个特定的类型，根据海萨尼 公理：
假定参与人类型的分布函数P （θ1,…, θn) 是所有参与人的共同知识，所有参与人知道P （θ1,…, θn)，所有参与人知道所有参与人知道 P （θ1,…, θn)，如此等等。 这意味着在进入市场的博弈中，如果进入者 有一种类型，在位者有两种类型，那么p是共同知 识，即进入者知道在位者是高成本的概率是p，进 入者知道在位者知道进入者知道在位者是高成本 的概率是p，如此等等，即在博弈开始时，所有参 与人有关自然行动的信念（belief）是相同的。
海萨尼转换
类型：一个参与人拥有的所有的个人信息（即所有不是共同知
识的信息）称为他的类型。 根据这个定义，甚至允许参与人不知道其他参与人是否知道自己 的类型。
例如：市场进入博弈：在位者不知道进入者是否知道自己是高成 本还是低成本，只知道进入者有p’的概率知道自己的成本函数， （1-p’）的概率不知道自己的成本函数。
真正的“信息不对称”
一个古董商发现一个人用珍贵的茶碟做 猫食碗，于是假装对这只猫很感兴趣， 要丛主人手里买下，主人不卖，为此古 董商出了大价钱。成交之后，古董商装 做不在意地说：这个碟子它已经用惯了， 就一块送给我吧。猫主人不干了：你知 道用这个碟子，我已经卖了多少只猫了？
第4章 不完全信息静态博弈
q2*
Ac 3
q1
A 2c
(
* cH 3
(1 )*cL )
A
2c
*c 3
(1 )*c
Ac 3
q2H
2A 2c (3 )*cH 6
(1 )*cL
2A 2c (3 )*c (1 )*c 6
二、先验判断和海萨尼转换
海萨尼提出了引入“自然（Nature）”的想法，将先验 概率（Prior Probability）转化为由“自然”最先进行选 择的模式。
也就是说：潜在进入者对在位者的类型有一个先验判断： 在位者为“高效型”企业的概率为“p”，在位者为低效 型企业的概率为“1 - p”。将这种先验信念转化为“自 然”的选择。
在位者的策略空间s斗争斗争斗争默许默许斗争默许默当在位者为高效型时在位者考虑在斗争和默许两种策略之间选择斗争是在位者的严格占优策略当在位者为高效型时不管潜在进入者选择进入还是不进入在位者都将选择斗争三求解不完全信息市场争夺战博弈当在位者为低效型时在位者考虑在斗争和默许两种策略之间选择时默许是在位者的严格占优策略当在位者为低效型时不管潜在进入者选择进入还是不进入在位者都将选择默三求解不完全信息市场争夺战博弈在位者会选择斗争默许作为自己的策略即在位者是高效型企业时在位者选择斗争
一、不完全信息与“市场争夺战”博弈
如果在位者是一个“不善于斗争”的低效型在位者。 “默许”是在位者的严格占优策略。 在位者一定会选择“默许”，潜在进入者会选择 “进入”。 博弈的纳什均衡是：（在位者选择“默许”，潜 在进入者选择“进入”）。
一、不完全信息与“市场争夺战”博弈
在位者究竟是“高效型”还是“低效型”？ 在位者知道自己的信息，但潜在进入者不知道在位者
非完全信息静态博弈
知道企业1知道自己的信息优势。
古诺博弈:企业2的产量选择
• 企业2的边际成本较高时和较低时，他希望生产的产出水平是不同的 （一般而言，前一种情况时的产出要更低一些）。 • 企业1从自己的角度，也会预测到企业2根据其成本情况将选择不同的 产量。 * * * (cH )和 q2 (cL ) 分别把企业的产量选择并表示为成本的函数，并令 q1 • 用 q2 * 表示企业1的单一产量选择。如果企业2的成本较高，他会选择 q2 (cH ) 满足：
一个n人静态贝叶斯博弈的标准式表述
定义 一个n人静态贝叶斯博弈的标准式表述包括：参与
人的行动空间 A1,…An，它们的类型集空间T1, …Tn，他们的
信念 p1, …pn以及他们的收益函数 u1, …un。参与人 i的类型 ti作为参与人 i的私人信息，决定了参与人 i的收益函数 ui (a1, …an;ti)，并且是可能的类型集Ti中的一个元素。参与 人 i的信念 pi ( t-i| ti)描述了 i在给定自己的类型 ti 时，对其他 n-1个参与人可能的类型 t-i的不确定性。我们用 G = {A1, …An;T1, …Tn;p1, …pn;u1, …un}
双向拍卖: 线性贝叶斯纳什均衡-5
• 双向拍卖中当且仅当pb≥ps时，交易才会发生。 • 在线性贝叶斯纳什均衡中，当且仅当vb﹥vs+1/4时，交 易才会发生，如图3.2
在这样定义参与人的类型之后，说参与人 i知道自己的收益函数也就 等同于说参与人 i知道自己的类型，类似地，说参与人 i可能无法确定其他 参与人的收益函数，也就等同于说参与人 i不能确定其他参与人的类型， 我们用 t-i={t1, …,ti-1,ti+1, …,tn}表示，并用 T-i表示 t-i所有可能的值的集合， 用概率 pi( t-i| ti)表示参与人在知道自己的类型是 ti的前提下，对其他参与 人类型（即 t-i）的信念（belief）。 在3.2节分析的所有应用中，参与人之间的类型是相互独立的，这种 情况下 pi( t-i| ti)与 ti不相关，于是我们可以把参与人的信念写成P1, …Pn。 但是，也存在参与人之间类型相关的情况，所以在给定静态贝叶斯博弈的 定义时，我们考虑到这种情况，仍把参与人的信念写为pi(t-i|ti)。
第四章 不完全信息静态博弈
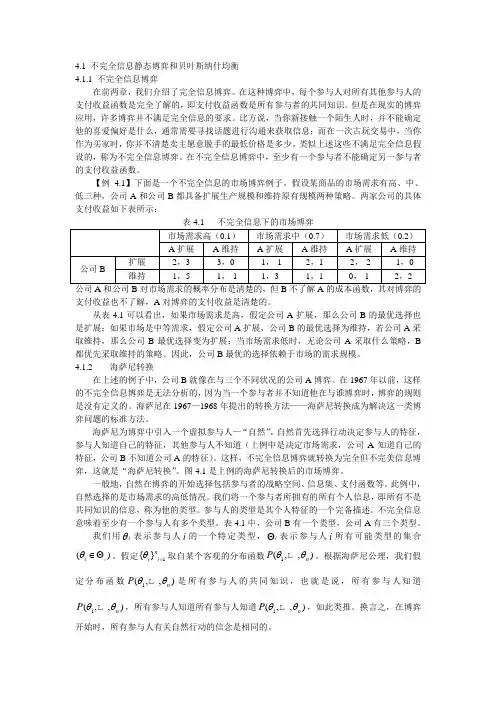
4.1 不完全信息静态博弈和贝叶斯纳什均衡4.1.1 不完全信息博弈在前两章，我们介绍了完全信息博弈。
在这种博弈中，每个参与人对所有其他参与人的支付收益函数是完全了解的，即支付收益函数是所有参与者的共同知识。
但是在现实的博弈应用，许多博弈并不满足完全信息的要求。
比方说，当你新接触一个陌生人时，并不能确定他的喜爱偏好是什么，通常需要寻找话题进行沟通来获取信息；而在一次古玩交易中，当你作为买家时，你并不清楚卖主愿意脱手的最低价格是多少。
类似上述这些不满足完全信息假设的，称为不完全信息博弈。
在不完全信息博弈中，至少有一个参与者不能确定另一参与者的支付收益函数。
【例 4.1】下面是一个不完全信息的市场博弈例子。
假设某商品的市场需求有高、中、低三种，公司A 和公司B 都具备扩展生产规模和维持原有规模两种策略。
两家公司的具体支付收益如下表所示：公司A 和公司B 对市场需求的概率分布是清楚的，但B 不了解A 的成本函数，其对博弈的支付收益也不了解，A 对博弈的支付收益是清楚的。
从表4.1可以看出，如果市场需求是高，假定公司A 扩展，那么公司B 的最优选择也是扩展；如果市场是中等需求，假定公司A 扩展，公司B 的最优选择为维持，若公司A 采取维持，那么公司B 最优选择变为扩展；当市场需求低时，无论公司A 采取什么策略，B 都优先采取维持的策略。
因此，公司B 最优的选择依赖于市场的需求规模。
4.1.2 海萨尼转换在上述的例子中，公司B 就像在与三个不同状况的公司A 博弈。
在1967年以前，这样的不完全信息博弈是无法分析的，因为当一个参与者并不知道他在与谁博弈时，博弈的规则是没有定义的。
海萨尼在1967—1968年提出的转换方法——海萨尼转换成为解决这一类博弈问题的标准方法。
海萨尼为博弈中引入一个虚拟参与人—“自然”，自然首先选择行动决定参与人的特征，参与人知道自己的特征，其他参与人不知道（上例中是决定市场需求，公司A 知道自己的特征，公司B 不知道公司A 的特征）。
博弈论与信息经济学4
解反应函数得纳什均衡为：
1 * * q1 q2 (a c) 3
垄断利润为：
1 * * 1 (q1* , q2 ) 2 (q1* , q2 ) (a c) 2 9
案例1 库诺特（Cournot）寡头竞争模型
为什么说库诺特（Cournot）寡头竞争模型是 典型的囚徒困境问题？ 垄断企业的问题：
敌人：四种部署方案 A 三个师都驻守甲方； B 两个师驻守甲方，一个师驻守乙方 C 一个师驻守甲方，两个师驻守乙方 D 三个师都驻守乙方 我军： a 集中全部兵力从甲方进攻 b 兵分两路，一个从甲方，一个从乙方，同时进攻 c 集中兵力从乙方进攻
A a b c
B
C
D
纳什均衡应用举例
Max Q(a Q c)
Q
寡头竞争的总产量大 于垄断产量的原因是：
垄断企业的最优产量：
Q* 1 2 * * (a c) q1 q2 (a c) 2 3
垄断利润为：
m (a c) 2 (a c) 2
1 4 2 9
每个企业在选择自己 的最优产量时，只考虑 对本企业利润的影响， 而忽视了对另外一个企 业的外部负效应。
案例2 公共地的悲剧
当草地上羊很少时，增加一只羊也许不会对其 他羊的价值有太大影响，但随着羊的不断增加， 每只羊的价值将急剧下降。
v 2v 0, 2 0 G G
参与人：农民 战略： 养羊的数量 支付： 利润 Gmax G v
案例2 公共地的悲剧
假设一只羊的价格为c，对于农民i来讲，其利 润函数为：
纳什均衡应用举例
不完全信息静态博弈
假设我们观察到一个人干了一件好事,那么,这个人 是好人的后验概率为: P(GP |GT)= P(GT|GP定张三是好人的先验概率是0.5, 那么, 在观察到张三干了一就好事后,我们如何修正他是好 人的先验概率依赖于我们认为这间好事好到什么程度. 1,这是一件非常好的好事,好人一定干,坏人决不可能 干,即P(GT|GP)=1, P(GT|BP)=0
进入者似乎是与两个不同的在位者博弈, 一个是高成本的在位者,一个是低成本的 在位者.
不完全信息古诺模型 参与人的类型是成本函数.假设逆需求函数 为P = a-q1-q2,每个企业的单位成本不变, 为ci,则企业的利润函数为: πi = qi (a-q1-q2-ci), i=1,2
假设企业1的单位成本c1是共同知识,企 业2的单位成本可能是高的也可能是低的, 企业2知道自己的成本类型,但企业1只 知道企业2属于这两种类型的概率分布 和1-,是共同知识. 进一步假设 a = 2, h c 2 = 1.25, = 0.5 c1 = 1, l c2 = 0.75,
不完全信息静态博弈: 不完全信息静态博弈:贝叶斯纳什均衡
完全信息博弈的基本假设是所有的参与人都知 道博弈的结构,博弈的规则,和博弈的支付函 数.例如在"市场进入"博弈中,进入者知道 在位者的偏好,战略空间和各种战略组合下的 利润水平,反之亦然.当然,这个假设在许多 情况下是不成立的.
哈桑尼( 哈桑尼(Harsanyi)定义了"贝叶斯纳什均衡": )定义了"贝叶斯纳什均衡" 贝叶斯均衡是纳什均衡在不完全信息博弈中的 扩展:
在静态不完全信息博弈中,参与人同时行动,没有机 会观察到其他人的选择; 每个参与人仅知道其他参与人类型的概率分布而不知 道其真实类型; 他不可能准确地知道其他参与人实际上会选择什么战 略,但是,他能正确地预测到其他参与人的选择是如 何依赖于其各自的类型的 决策目标就是在给定自己的类型和别人的类型依从战 略的情况下,最大化自己的期望效用.
第4讲 不完全信息静态博弈
第4讲 不完全信息静态博弈
上述定义包含一种可能：参与人j可能具有参与人i类型的某种信息。进一 步，如果所有参与人的类型空间只包含一个元素，即对于所有的i， i ，不完全信息静态博弈就退化为完全信息静态博弈。换言之，完全 信息静态博弈可以理解为不完全信息静态博弈的一个特例（即分布函数P 是退化的）。另外，如果参与人的类型是完全相关的（perfectly correlated） ，当参与人i观测到自己的类型时也就知道了其他参与人的类型，博弈也是 完全信息的。不过，一般假定参与人的类型是相互独立的。
这样上述不完全信息博弈就转换为如下图所示的完全但不完美信息博弈可以使用标准的分析技术进行分析这就是所谓的海萨尼转化进入者进入不进入在位者在位者进入不进入斗争合作斗争合作030040501000400308010100海萨尼转换后的市场进入阻挠博弈1p在上述例子中我们假定自然选择的只是在位者是高成本还是低成本
第4讲 不完全信息静态博弈
在位者 高成本情况 低成本情况
默许
进入者 进入 不进入
斗争
默许
斗争
40，50 0，300
-10，0 0，300
30，80 0，400
-10，100 0，400
市场进入阻挠博弈：不完全信息
第4讲 不完全信息静态博弈
• 在这个例子中，进入者有关在位者的成本信息是 不完全的，但在位者知道进入者的成本函数。 • 从支付矩阵可以看出，如果在位者是高成本，给 定进入者进入，在位者的最优选择是默许；如果 在位者是低成本，给定进入者进入，在位者的最 优选择是斗争。因此，在完全信息情况下，如果 在位者是高成本，进入者的最优选择是进入，如 果在位者是低成本，进入者的最优选择是不进入。
第4讲 不完全信息静态博弈
第四章 不完全信息静态博弈
然”(Nature)
转化为
化不完全信息博弈
完全但不完美信息博弈
(1)Harsanyi转换例子
(2)类型
(3)静态贝叶斯博弈的时间顺序
(4)贝叶斯纳什均衡建立
Harsanyi转换例子
N
高
低
[P]
进入者
[1-P]
不进入 (0，300)
合作
进入
不进入
在位者 (0，400)
斗争
合作
进入
斗争
(40，50)
当在位者两种成本，进入者似乎是与两个不同的在位者博弈， (一高，一低) 。如在位者有T种可能的C，进入者似乎是在与T个不同 的在位者博弈。(在1967年以前，博弈论专家认为这样的不完全信息 博弈是没法分析的，因为当一个参与人并不知道他与谁博弈时，博弈 的规则是没定义的。)
处理：Harsanyi，1967-1968—引入虚拟的参与人—“自
低成本：给定进入者不进入，在位者的最优选择是斗争，概率1-P，认为在位者低成本
则进入者选择进入的期望利润
进入者选择不进入的期望利润
40P-10 (1-P)
≥
0×P+0 (1-P)=0
50P≥10 P≥1/5
即 P>1/5进入 P<1/5不进入 P=1/5两者无差异 就选进入(假定)
海萨尼(Harsanyi)转换
i
a
* i
(a1*
(1
),
,
a* i 1
(
i
1
),
a* i 1
(
i
1
),
,
a
* n
(
nБайду номын сангаас
))
博弈论与信息经济学讲义2012-2下+_2012[1].2.29晚_
纳什均衡与占优战略均衡及重复剔除的占优均 衡：
（1）每一个占优战略均衡及重复剔除的占优均衡一定 是纳什均衡，但并非每一个纳什均衡都是占优战略均 衡或重复剔除的占优均衡； （2）纳什均衡一定是在重复剔除严格劣战略过程中没 有被剔除掉的战略组合，但没有被剔除掉的组合不一 定是纳什均衡，除非它是唯一的（不适用于严格弱劣 战略的情况）
1，10 0，10 0，10
C3
1，12 0，11 0，13
剔除顺序：C2、R2、C1、R3，战略组合（R1，C3）
故一般使用严格劣战略剔除，可以看到，（R1，C3） （R1，C1）都是纳什均衡，但在这里是不可解的。
练习： 找出下列两队夫妻的纳什均衡
妻子 活着 恩爱夫妻 丈夫 活着 死了
2，2 0，-6
三 重复剔除的占优均衡
注意： 与占优战略均衡中的占优战略和劣战略不 同，这里的占优战略或劣战略可能只是相对于 另一个特定战略而言。
三 重复剔除的占优均衡
案例2-智猪博弈
小猪 按 大猪 按 5，1 等待 9，-1 等待 4，4 0，0 4大于1 0大于-1
按是小猪的严格 劣战略-剔除 “按”是大猪的占优战略，纳什均衡：大猪按，小猪等待
木村 北 北 肯尼 南 南
2，-2 1，-1
2，-2 3，-3
三 重复剔除的占优均衡
练习：在下列战略式表达中，找出重复剔除的 占优均衡
C1 R1 R2 R3
4，3 2，1 3，0
C2
5，1 8，4 9，6
C3
6，2 3，6 2，8
三 重复剔除的占优均衡
注意：
1、严格占优战略下，重复剔除的占优均衡结果 与劣战略的剔除顺序无关；弱占优战略下，重 复剔除的占优均衡结果与弱劣战略的剔除顺序 有关。 2、重复剔除的占优均衡要求每个参与人是理性 的，而且要求“理性”是参与人的共同知识。 即：所有参与人知道所有参与是理性的，所有 参与人知道所有参与人知道所有参与是理性的
不完全信息静态博弈
N
高 低
[P]
不进入
进入者
进入 不进入
[1-P]
进入 在位者
斗争
(0,300)
B
合作
在位者
斗争
(0,400)
B
合作
(40,50) (-10,0)
(30,80) (-10,100)
期望利润:p×40+(1-p)×(-10).为保证不亏,期望利润为0, 则p=0.2。大于0.2会赚钱。对p的判断就是“贝叶斯理念”
在位者 高成本情况 低成本情况 默许 斗争 默许 斗争 进入者 进入 40，50 -10，0 30，80 -10,100 不进入 0，300 0，300 0，400 0，400
• 2. 海萨尼转换（Harsanyi transformation）
– 引入一个虚拟的参与人“自然”，自然首先行动，选择 决定参与人的特征（如成本函数），参与人知道自己的 特征，其他参与人不知道。 – 这时，不完全信息博弈转换成完全但不完美信息博弈， 因为可以藉此展开分析 – 海萨尼转换已成为处理不完全信息博弈的标准方法 – 通过海萨尼转换，博弈开始时，所有参与人对“自然” 的行动有一致的信念，即都知道所有参与人类型的概率 分布函数。此即“海萨尼公理”
• 静态贝叶斯博弈的时间顺序为： 1、自然选择类型向量θ，参与人i能观测到自己的 类型θi，但参与人j只知道pj=pj(θ-j|θj )，但不知道 参与人i的类型。 2、n个参与人同时行动； 3、参与人i得到类型依存支付函数ui(a1,…an;θi )。 • 给定参与人i只知道自己的类型而不知道其他参与 人的类型，参与人i将选择ai(θi)最大化自己的期望 效用。 • 贝叶斯纳什均衡（BNE）：n人不完全信息静态博 弈G的纯战略均衡是一个类型依存战略组合 {ai(θi)}i=1,…n，其中每个参与人i在给定自己的 类型θi和其他参与人类型依存战略a-i(θ-i)的情况下， 最大化自己的期望效用。
博弈论讲义2 非合作博弈理论
开发商A
开发 4000，4000 不开发 0，8000
8000，0 0，0
需求小的情况 开发商A
开发商B 开发 不开发
开发 -3000，-3000 1000，0
不开发 0，1000
0，0
博弈的战略式表述
一 、博弈的基本概念及战略表述
博弈论的基本概念包括： ✓ 参与人：博弈论中选择行动以最大化自己效用的决策主体； ✓ 行动：参与人的决策变量 ✓ 战略：参与人选择行动的规则 ✓ 信息：参与人在博弈中的知识，特别是有关其他参与人的特征和
一 、博弈的基本概念及战略表述
需求大的情况
开发商B 开发 不开发
开发商A
开发 4000，4000 不开发 0，8000
8000，0 0，0
需求小的情况 Βιβλιοθήκη 发商A开发商B 开发 不开发
开发 -3000，-3000 1000，0
不开发 0，1000
0，0
博弈的战略式表述
不完全信息动态博弈-精练贝叶斯纳什均衡 泽尔腾（1965）
一 、博弈的基本概念及战略表述
博弈的战略式表述：
战略式表述给出： 1、博弈的参与人集合：i , (1,2, , n); 2、每个参与人的战略空间：Si，i 1,2, , n; 3、每个参与人的支付函数：ui (s1, , si , , sn ),i 1,2, , n)
用G S1， ，Sn;u1, , un代表战略式表述博弈。
✓ 完美信息：指一个参与人对其他参与人（包括“自然”）的 行动选择有准确了解的情况，即每一个信息集只包含一个值。
✓ 完全信息：指自然不首先行动或自然的行动的初始行动所有 参与人观察到的情况。
✓ 共同知识：指“所有参与人知道所有参与人知道所有参与人 知道….”的知识。
博弈论-不完全信息静态博弈
从而V(b)=2b，或b=v/2
竞价者的最优战略是以自己保留价格的一 半作为叫价。
2021/4/9
24
一级密封价格拍卖（四）
如果有n人参与竞标，则b=(n-1)v/n，即b 随n的增加而增加，特别地，当n时， bv，就是说，投标人越多，卖者能得到 的价格就越高；当投标人趋于无穷时，卖 者几乎得到买者价值的全部。因此，让更 多的人加入竞标是卖者的利益所在。
不完全信息博弈
在生活中我们也会碰到这样的问题，比 如一个乞丐向你乞讨，你愿意帮助别人， 但不知道他是真的乞丐还是骗子，该如 何决定呢？如果你喜欢与人为善，你可 能愿意冒一点上当的危险，这不等于你 愚蠢，而是你认为，帮助一个困境中的 人比回绝一个骗子更重要。
2021/4/9
36
不完全信息博弈
❖ 不完全信息：每一个参与人对所有其他参与人 的（对手）的特征、战略空间及支付函数有准 确的 知识，否则为不完全信息。
不求爱 0，0
0，0
2021/4/9
33
市场需求信 息是不完全的。
不完全信息博弈
需求大的情况
开发商B 开发 不开发
开发商A
开发 4000，4000 不开发 0，8000
8000，0 0，0
需求小的情况 开发商A
开发商B 开发 不开发
开发 -3000，-3000 1000，0
不开发 0，1000
0，0
2021/4/9
32
不完全信息博弈
被求爱者对于
求爱者的品德的 信息是不完全的。
你 接受 不接受
求爱博弈：
求爱 100，100 -50，0
品德优良者求爱 求爱者 不求爱 0，0
0，0
100x+（-100）（1-x）=0
不完全信息静态博弈：贝叶斯纳什均衡
不完全信息静态博弈：贝叶斯纳什均衡海萨尼1、前两篇⽂章讲的博弈都包含⼀个基本假设，即所有参与⼈都知道博弈的结构、规则、⽀付函数，因⽽称为完全信息博弈。
然⽽现实中，参与者并不了解其他参与者的⼀些信息，即不完全信息博弈（games of incomplete information）。
2、当对⼿有多种情况时，⽐如市场博弈的例⼦，在位者成本函数可能有需求⾼、需求中、需求低三种情况，那么可以采取“海萨尼转换”，即引⼊⼀个虚拟的参与⼈“⾃然”，⾃然⾸先⾏动，选择参与⼈的类型，被选择的参与⼈知道⾃⼰的真实类型，其他参与⼈并不清楚这个参与⼈的真实类型，但知道各种可能类型的概率分布。
如下图所⽰：3、这种情况下，可以通过海萨尼转换（Harsanyi transformation）把不完全信息博弈转换成完全但不完美信息博弈（complete but inprefer information）。
“不完美信息”指“⾃然”作出了选择，但其他参与⼈并不知道它的具体选择是什么，仅知道各种选择的概率分布。
4、在静态不完全信息博弈中，参与⼈同时⾏动，每个参与⼈的最优战略依赖于⾃⼰的类型，他不可能准确的知道其他参与⼈实际上会做出什么选择，但他能正确的预测其他参与⼈的选择是如何依赖于各⾃的类型的。
决策的⽬标就是在给定⾃⼰的类型和别⼈的类型依从战略的情况下，最⼤化⾃⼰的期望效⽤。
海萨尼定义了“贝叶斯纳什均衡”，给定⾃⼰的类型和别⼈类型的概率分布，每个参与⼈的期望效⽤达到了最⼤化，没有⼈有积极性选择其他战略。
5、举个例⼦，某⼀市场原来被A企业所垄断，现在B企业考虑是否进⼊。
B企业知道，A企业是否允许它进⼊，取决于A企业阻挠B企业进⼊所花费的成本。
如果阻挠的成本⾼，A企业的最优战略是默许B进⼊。
如果阻挠的成本低，A企业的最优战略是阻挠。
⽀付矩阵如下表所⽰：B企业并不知道A企业的阻挠成本是⾼还是低。
这⾥，某⼀参与⼈本⼈知道、其他参与⼈不知道的信息称为私⼈信息。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
主要内容简介
第二篇 信息经济学
第六章 委托-代理理论（I） 第七章 委托-代理理论（II） 第八章 逆向选择与信号传递
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈
海萨尼转换
不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例
默许
斗争 默许 斗争 进入 不进入
进入者
-3, -3 0, 1
-3, -3 0, 0
1, 0 0, 1
1, 0 0, 0
进入者的最优选择依赖于他在多大程度上认为在位者 是低成本的。
假定进入者认为在位者是高成本的概率是p，低成本的概率是（1-p）， 那么，进入者选择进入的期望利润是p（40）+（1-p）（-10），选择不 进入的利润是0，因此，进入者的最优选择是：如果p>=1/5，进入，如 果p<1/5，当p=1/5时，进入与不进入是无差异的，我们假定其进入。
“空城计”
街亭失守，司马懿引大军蜂拥而来，当时 孔明身边只有一班文官，军士一半已经运粮草 去了，只有2500军士在城中。 众官听得这个消息，尽皆失色。孔明登城 望之，果然尘土冲天，魏兵分两路杀来。
孔明令众将旌旗尽皆藏匿，打开城门，每 一门用20军士，扮作百姓，洒扫街道。而孔明 羽扇纶巾，引二小童携琴一张，于城上敌楼前 凭栏而望，焚香操琴。
博弈论与信息经济学
（Game Theory and Information Economics )
张玲玲
中国科学院研究生院管理学院 zhangll@
主要内容简介
第一章 概述-人生处处皆博弈
第一篇 非合作博弈理论
第二章 第三章 第四章 第五章
完全信息静态信息博弈-纳什均衡 完全信息动态搏弈-子博弈精炼纳什均衡 不完全信息静态博弈-贝叶斯纳什均衡 不完全信息动态博弈-精练贝叶斯纳什均衡
海萨尼转换
设θi表示参与人i的一个特定的类型，根据海萨尼 公理：
假定参与人类型的分布函数P （θ1,…, θn) 是所有参与人的共同知识，所有参与人知道P （θ1,…, θn)，所有参与人知道所有参与人知道 P （θ1,…, θn)，如此等等。 这意味着在进入市场的博弈中，如果进入者 有一种类型，在位者有两种类型，那么p是共同知 识，即进入者知道在位者是高成本的概率是p，进 入者知道在位者知道进入者知道在位者是高成本 的概率是p，如此等等，即在博弈开始时，所有参 与人有关自然行动的信念（belief）是相同的。
4000，4000 0，8000 8000，0 0，0
开发商A
不开发 需求小的情况
开发
开发商B 开发
-3000，-3000 0，1000
不开发
1000，0 0，0
开发商A
不开发
房地产开发博弈
不完全信息博弈
进入者关于 在位者成本信息 是不完全的。
市场进入博弈：不完全信息 在位者 低成本情况 高成本情况
在信息不充分的情况下，博弈参与者 不是使自己的支付或效用最大，而是使 自己的期望效用或支付最大。 如让你在50%的概率获得100元与10% 的概率获得200元两者之间选择的话，前 者的期望所的是50元，后者是20元，故 选前者。
被求爱者对于 求爱者的品德的 信息是不完全的。
不完全信息博弈
你
接受 求爱博弈： 品德优良者求爱 求爱
不完全信息博弈
在生活中我们也会碰到这样的问题，比 如一个乞丐向你乞讨，你愿意帮助别人， 但不知道他是真的乞丐还是骗子，该如 何决定呢？如果你喜欢与人为善，你可 能愿意冒一点上当的危险，这不等于你 愚蠢，而是你认为，帮助一个困境中的 人比回绝一个骗子更重要。
不完全信息博弈
不完全信息：每一个参与人对所有其他参与人 的（对手）的特征、战略空间及支付函数有准 确的 知识，否则为不完全信息。
被求爱者对于求爱 者的品德的信息是不完 全的。
练习-将下列博弈进行海萨尼转换
你
接受 求爱博弈： 品德优良者求爱 求爱
100，100
不接受
-50，0 0，0
求爱者
不求爱 0，0
求爱者品德优良的概率是p
你
求爱博弈： 品德恶劣者求爱 求爱者 接受 求爱 不接受
0，0 100，-100 -50，0
不求爱 0，0
类似上述情况称为不完全信息博弈，即在不完 全信息博弈中，至少有一个参与人不知道其他 参与人的支付函数。
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈
海萨尼转换
不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例
第i个企业的利润函数为：
静态贝叶斯博弈的时间顺序为： 1、自然选择类型向量，参与人i能观测到自己的类 型，但参与人j只知道除i之外所有参与人类型，但 不知道参与人i的类型。 2、n个参与人同时行动； 3、参与人i得到类型依存支付函数。
给定参与人i只知道自己的类型而不知道其他参与 人的类型，参与人i将选择使自己的效应最大化的 期望效用。 贝叶斯纳什均衡：n人不完全信息静态博弈的纯战 略均衡是一个类型依存战略组合，其中每个参与人 i在给定自己的类型θi和其他参与人类型依存战略 的情况下，最大化自己的期望效用。
这种情况下，进入者也有两种类型：知道（在位者的成本）或不 知道（在位者的成本）。 例如：在谈判中，甲方知道自己是强硬派或妥协派，乙方知道自 己是否知道甲方是强硬派或妥协派，但甲方不知道乙方是否知道 自己是强硬派还是妥协派，则甲方有两种类型：强硬派或妥协派， 乙方有两种类型：知道或不知道。 不完全信息意味着，至少有一个参与人有多个类型。
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈
海萨尼转换
不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例
三 贝叶斯纳什均衡与混合战略均衡
四 机制设计理论与显示原理
不完全信息静态博弈 -贝叶斯纳什均衡
在不完全信息静态博弈中，所有参与人同时行动，其 战略空间等于行动空间，但是参与人i的行动空间
参与人：企业1、企业2； 行动顺序：同时行动
不完全信息：企业1单位成本c1是共同知识，企业2的成 本可能是c2l或c2h，企业1只知道c2=c2l的可能性是1/2，这 是共同知识。
不完全信息库诺特模型
企业1
企业2
qi ：第i个企业的产量 Ci：代表第i个企业的成本
假定逆需求函数为：P(Q) a (q1 q2 )
海萨尼转换
类型：一个参与人拥有的所有的个人信息（即所有不是共同知
识的信息）称为他的类型。 根据这个定义，甚至允许参与人不知道其他参与人是否知道自己 的类型。
例如：市场进入博弈：在位者不知道进入者是否知道自己是高成 本还是低成本，只知道进入者有p’的概率知道自己的成本函数， （1-p’）的概率不知道自己的成本函数。
不完全信息博弈
司马懿自马上远远望之，见诸葛亮神态自 若，顿时心生疑忌，犹豫再三，难下决断。又 接到远山中可能有埋伏的情报，于是叫后军做 前军，前军做后军，急速退去。司马懿之子司 马昭问：“莫非诸葛亮无军，故做此态，父何 故便退兵？”
司马懿说：“亮平生谨慎，不曾弄险，今 大开城门，必有埋伏，我兵若进，必中计也。” 孔明见魏军退去，抚掌而笑，众官无不骇 然。诸葛亮说，司马懿“料吾生平谨慎，必不 弄险，疑有伏兵，所以退去。吾非行险，盖因 不得已而用之，弃城而去，必为之所擒。”
第四章 不完全信息静态博弈 -贝叶斯纳什均衡
一 不完全信息静态博弈和贝叶斯纳什均衡
不完全信息博弈
海萨尼转换
不完全信息静态博弈的战略式表述和贝叶斯纳什均衡
二 贝叶斯纳什均衡应用举例
三 贝叶斯纳什均衡与混合战略均衡
四 机制设计理论与显示原理
不完全信息库诺特模型
企业1
企业2
诸葛亮：处于劣势，但知道博弈的结构，比对方掌握更多的信息。 计策：使用各种手段迷惑司马懿，为的是不让对方知道其策略的结果（支 付）。迫使其认为，撤退比进攻好，降低其进攻的预期收益。
如用概率论的术语来说，诸葛亮的做法是加大司马懿对进攻失败的主
观概率，使司马懿认为进攻的期望收益小于撤退的期望收益。
不完全信息博弈
三 贝叶斯纳什均衡与混合战略均衡
四 机制设计理论与显示原理
不完全信息博弈-无法避免的不确定性
有一次，主人派伊索进城。半路上，他遇 见一位法官。
法官严厉地盘问：“你要去哪儿？”
“不知道”伊索回答说。
法官起了疑心，派人把伊索关进了监狱， 严加审问。 “法官先生，要知道，我讲的是实话。” 伊索说，“我确实不知道我会进监狱”。
三 贝叶斯纳什均衡与混合战略均衡
四 机制设计理论与显示原理
海萨尼转换
市场进入博弈：不完全信息
高成本情况
默许
斗争 进入 不进入
在位者
低成本情况
默许 斗争
进入者
-3, -3 0, 1
-3, -3 0, 0
1, 0 0, 1
1, 0 0, 0
进入者似乎在与两个在位者博弈，一个是高成本的在 位者，一个是低成本的在位者；如果在位者有T种不同的成本 函数在位者就相当于与T个不同的在位者博弈。
可能依赖于其类型，也就是行动空间是类型依 存的。类似的，其支付函数也是类型依存的。如企业