扩散与固相反应

第七章
扩散与固相反应
材料科学与工程研究院
1
本章主要内容


7.1 固体中扩散基本特点与宏观动力学方程 7.2 扩散机制和扩散系数
7.3 影响扩散因素 7.4 固相反应
2
7.1 固体中扩散基本特点与 宏观动力学方程
一、固体中扩散的基本特点 二、Fick第一定律与稳定扩散
三、Fick第二定律与不稳定扩散
随时间变化。
7
Fick第一定律： 单位时间内通过垂直于扩散方向的单位面
积上扩散的物质数量和浓度梯度成正比。
数学表达式：
C J＝－D x
J 扩散通量，单位时间通过单位截面的质点数(质点数/s/cm2)
D 扩散系数，单位浓度梯度的扩散通量 (m2/s 或 cm2/s)
C 质点数/cm3
“ － ” 表示粒子从高浓度向低浓度扩散，即逆浓度梯度方向扩散
△G
间隙原子扩散势场示意图
5
用途
离子晶体的导电 固溶体的形成 相变过程 硅酸盐 所有过程 固相反应 烧结
金属材料的涂搪瓷
陶瓷材料的封接 耐火材料的侵蚀性
6
二、Fick第一定律与稳定扩散
稳定扩散： 扩散质点浓度不随时间变化
C 0 t
推 动 力： 浓度梯度
特 点： 扩散过程中体系内部各处扩散质点的浓度不
1 C 1 C J＝ .( 2 ) 2 . 2 x 2 x
由Fick第一定律 x 3 1 2
17
1 2 一 维 D＝ λ τ 2
三维
1 2 D＝ 6
1 2 一 维 D＝ λ τ 2
三维
1 2 D＝ 6
无规则行走扩散的系数取决于两原子间距 和跃迁频率 ！

A
概述
四、扩散的意义
无机非金属材料制备工艺中很多重要的物理化学过程 都与扩散有关系。例如，固溶体的形成、离子晶体的 导电性、材料的热处理、相变过程、氧化、固相反应 、烧结、金属陶瓷材料的封接、金属材料的涂搪与耐 火材料的侵蚀。因此研究固体中扩散的基本规律的认 识材料的性质、制备和生产具有一定性能的固体材料 均有十分重大的意义。
A
第一节 宏观动力学方程
一、稳定扩散和不稳定扩散
稳定扩散：
扩散物质在扩散层内各处的浓度不 随时间而变化，即dc/dt=0
不 间而变化，即dc/dt0
A
第一节 宏观动力学方程
二、扩散的动力学方程
1、菲克第一定律（Fick’s First Law）
在扩散体系中，参与扩散质点的浓度因位置而异、且可随时间 而变化。
A
第一节 宏观动力学方程
2、 菲克第二定律（Fick’s Second Law）
如图10-2所示，通过横截面积为A，相距为 dx的微小体积元前后的流量分别为J1和J2。 由物质平衡关系可得出：流入Adx体积元的 物质量减去流出该体积的量即为积存在微小 体积元中的物质量。 物质流入速率=J1A
物质流出速率 J2AJ1(JxA )dx 物质积存速率 J1AJ2A J x•A•dx
公式 ：
Jx=-Ddc/dx
式中 Jx—— 扩散通量。即单位时间单位 面积上溶质扩散的量。 由于扩散有方向性，故J为矢量, 对于三维有如下公式：
JD(icjckc) x y z
A
第一节 宏观动力学方程
菲克第一定律是质点扩散定量描述的 基本方程。它适于稳定扩散（浓度分 布不随时间变化），同时又是不稳定 扩散（质点浓度分布随时间变化）动 力学方程建立的基础。

§7.5 固相反应及其机理
一,固相反应的定义
广义:凡是有固相参与的化学反应,都可称为固 广义:凡是有固相参与的化学反应, 相反应 .
如:固体热分解,氧化及固-固,固-液间的化学反应 固体热分解,氧化及固-
狭义: 狭义:固体与固体间发生化学反应生成新的固体 产物的过程. 产物的过程.
二,固相反应的特点
则,过程为扩散速度控制,称为扩散动力学范围 过程为扩散速度控制,称为扩散动力学范围 (3)当扩散速度远和化学反应速度相当时,即 K ～ D/ δ )当扩散速度远和化学反应速度相当时, 1 1 V= = 1 δ 1 1 + + KC0 DC0 VR max VD max 则,过程速度由上式确定,称为过渡范围 过程速度由上式确定,称为过渡范围 固相反应总速度: 固相反应总速度:
F1 (G) = (1 G) 1 = K1t ′ F2 (G) = ln(1 G) = K1 t
实验验证: 实验验证:
[
2 3
]
(球形模型) 球形模型) (平板模型) 平板模型)
如 NaCO3:SiO2=1:1 ,在740℃下进行固相反应:
Na2CO3 ( s ) + SiO2 ( s ) → Na2 SiO3 + CO2 ( g )
V = VR = VD
则:
KC = D
C0 C
δ
M-MO界面氧浓度: - 界面氧浓度: 界面氧浓度
C0 C= 1 + Kδ D
1 δ + KC0 DC0 1
得:
V = VR = KC =
1 1 1 ∴ = + V KC0 DC0 δ
讨论: 讨论:(1)当扩散速度远大于化学反应速度时,即 K << D/δ 当扩散速度远大于化学反应速度时, 当扩散速度远大于化学反应速度时

0



e

2
d
0
第二种情况
C ( x, t )
Q 2 Dt
exp(
x
2
)
4 Dt
第三节
一、扩散推动力
扩散机理和扩散系数
根据热力学，扩散过程的发生与否与系统中化学势有根 本的关系，物质从高化学势流向低化学势是一个普遍规 律，一切影响扩散的外场（电场、磁场、应力场等）都 可以统一于化学势梯度之中。 因此，扩散推动力的本质是化学势梯度，而且只有当化 学势梯度为零时系统扩散方可达到平衡；浓度梯度不是 质点定向扩散推动力的实质。
由热力学理论可知，在多组分的多相系统中任一组分i由α
相迁移到相中，迁移量为dni mol，系统的吉布斯自由能 的变化为： dG dn dn
i i i i
要使上述迁移过程自发进行，必须是 ：
dG i dni i dni 0
因式中 dni＞0，所以：
不稳定扩散根据边界条件分为两种情况：
一是扩散物质浓度（C0）在晶体表面保持不变； 二是一定量（Q）的物质由表面向晶体内部扩散。
c c0
c
x
x
第一种情况
C ( x, t ) C0 erfc(
erf ( ) 2
x 2 Dt
)
2



e

2
d ,
erfc( ) 1
a、金属离子空位型
造成这种非化学计量空位的原因往往是环境中氧分压升 高迫使部分Fe2+ 、Ni2+ 、Mn2+ 等二价过渡金属离子变成 三价金属离子，如：
2M
M

第七章 扩散与固相反应1、名词解释：非稳定扩散：扩散过程中任一点浓度随时间变化；稳定扩散：扩散质点浓度分布不随时间变化。

无序扩散：无化学位梯度、浓度梯度、无外场推动力，由热起伏引起的扩散。

质点的扩散是无序的、随机的。

本征扩散：主要出现了肖特基和弗兰克尔点缺陷，由此点缺陷引起的扩散为本征扩散（空位来源于晶体结构中本征热缺陷而引起的质点迁移）；非本征扩散：空位来源于掺杂而引起的质点迁移。

正扩散和逆扩散：正扩散：当热力学因子时，物质由高浓度处流向低浓度处，扩散结果使溶质趋于均匀化，D i >0。

逆扩散：当热力学因子 时，物质由低浓度处流向高浓度处，扩散结果使溶质偏聚或分相，D i <0。

2、简述固体内粒子的迁移方式有几种?答 易位，环转位，空位扩散，间隙扩散，推填式。

3、说明影响扩散的因素？化学键：共价键方向性限制不利间隙扩散，空位扩散为主。

金属键离子键以空位扩散为主，间隙离子较小时以间隙扩散为主。

缺陷：缺陷部位会成为质点扩散的快速通道，有利扩散。

温度：D=D 0exp （-Q/RT ）Q 不变，温度升高扩散系数增大有利扩散。

Q 越大温度变化对扩散系数越敏感。

杂质：杂质与介质形成化合物降低扩散速度；杂质与空位缔合有利扩散；杂质含量大本征扩散和非本征扩散的温度转折点升高。

扩散物质的性质：扩散质点和介质的性质差异大利于扩散；扩散介质的结构：结构紧密不利扩散。

4、在KCl 晶体中掺入10-5mo1％CaCl 2，低温时KCl 中的K +离子扩散以非本征扩散为主，试回答在多高温度以上，K +离子扩散以热缺陷控制的本征扩散为主？（KCl 的肖特基缺陷形成能ΔH s =251kJ/mol ，R=8.314J/mo1·K ） 解：在KCl 晶体中掺入10-5mo1％CaCl 2，缺陷方程为：2'22KCl K K cl CaCl Ca V Cl ∙⨯−−−→++则掺杂引起的空位浓度为'710K V -⎡⎤=⎣⎦欲使扩散以热缺陷为主，则''K K V V ⎡⎤⎡⎤>⎣⎦⎣⎦肖 即7exp()102s H RT-∆-> 即7251000exp()1028.314T -->⨯ 解得T>936.5K5、（1）试述晶体中质点的扩散机构及方式。

′′ [VFe ] =
1 1 ( )3
4
1 PO2 6
exp(− ∆G / 3 RT )
或DFe 2 + / Fe
FK
3
= KK t
扩散 • 1非稳定扩散：扩散过程中任一点浓度随时间变化。 非稳定扩散： 非稳定扩散 • 稳定扩散 稳定扩散：扩散质点浓度分布不扩散： 热起伏引起的扩散。质点的扩散是无序的、随机的。 • 3互扩散：多元系统往往存在着几种离子同时进行的扩散 ， 互扩散： 互扩散 有浓度差的空间扩散称为互扩散。 互扩散推动力： 互扩散推动力：化学位梯度。 • 4 间隙扩散：质点沿间隙位置扩散。 间隙扩散： • 5 本征扩散：主要出现了肖特基和弗兰克尔点缺陷，由此点 本征扩散： 缺陷引起的扩散为本征扩散（空位来源于晶体结构中本征热 缺陷而引起的质点迁移）。 非本征扩散： 非本征扩散：空位来源于掺杂而引起的质点迁移。 • 6.菲克第一定律：J=-Ddc/dx，菲克第一定律应用于稳定扩散 菲克第一定律： 菲克第一定律 菲克第二定律： 菲克第二定律：dc/dt=Dd2c/dx2，菲克第二定律应用于非稳 定扩散。
4、 固相中的扩散 、
D = D0 . exp(−
∆Hm + ∆H f / 2 RT
)
LnD
∆H m + ∆H f / 2 (本征扩散 本征扩散) 本征扩散 − R ∆H m + ∆H 0 / 3 E (非化学计量扩散 非化学计量扩散) 非化学计量扩散 − R ∆H m − (非本征扩散或杂质扩散 非本征扩散或杂质扩散) 非本征扩散或杂质扩散 F R
1/T
5、固相反应的动力学方程 、 化学动力学范围： 化学动力学范围：
扩散动力学范围： 扩散动力学范围：
1 F0 (G) = 1 − (1 − G)3 = K0t 2 － F (G) = (1 − G) 3－ ＝K1t 1 1 1 FJ (G) = [1 − (1 − G)3 ]2 = K J t

第七章 扩散与固态相变（一）
25/11/2018
1
概述
扩散现象：气体和液体中，例如在房间的某处打开一瓶 香水，慢慢在其他地方可以闻到香味，在清水中滴入一滴墨 水，在静止的状态下可以看到他慢慢的扩散。 扩散：由构成物质的微粒 ( 离子、原子、分子 ) 的热运动 而产生的物质迁移现象称为扩散。扩散的宏观表现是物质的 定向输送。
25/11/2018
34268s = 9.52hr
27
例2 一铁棒中碳的原始浓度为0.20%。现在1273K的温度下对 其进行渗碳处理，试确定在距表面0.01cm处碳浓度达到 0.24%所需的时间。已知在渗碳气氛中，铁棒的表面碳浓度 维持在0.40%；碳在铁中的扩散系数与温度的关系为
D (2 105 m 2 / s){exp[(142000 J / mol) / RT ]}
dC J D dx
25/11/2018 18
2） 扩散第二方程
解决问题的关键:搞清问题的起始条件和边界条件，并假定任一时 刻t溶质的浓度是按怎样的规律分布。 对不同的实际问题，可采用不同的浓度分布形式来处理，如正态分 布、误差分布、正弦分布、指数分布等。
解析解通常有高斯解、误差函数解和正弦解等
一维无限长棒中扩 散方程误差函数解：
25/11/2018 30
water
25/11/2018
adding dye
partial mixing
homogenization
time
2
说明
在固体材料中也存在扩散，并且它是固体中物 质传输的唯一方式。因为固体不能象气体或液体那
样通过流动来进行物质传输。即使在纯金属中也同
样发生扩散，用掺入放射性同位素可以证明。 扩散在材料的生产和使用中的物理过程有密切 关系，例如：凝固、偏析、均匀化退火、冷变形后 的回复和再结晶、固态相变、化学热处理、烧结、

实验28 热重分析技术在固相反应研究中的应用一、实验目的固相反应是材料制备中一个重要的高温动力学过程，固体之间能否进行反应、反应完成的程度、反应过程的控制等直接影响材料的显微结构，并最终决定材料的性质，因此，研究固体之间反应的机理及动力学规律，对传统和新型无机非金属材料的生产有重要的意义。

本实验的目的：1.掌握TG法的原理，熟悉采用TG法研究固相反应的方法。

2.通过CaCO3-SiO2系统的反应验证固相反应的动力学规律─杨德方程。

3.通过作图计算出反应的速度常数和反应的表观活化能。

二、实验原理许多固体材料在在高温下加热时，因其中的某些组分分解逸出或固体与周围介质中的某些物质作用使固体物系的重量发生变化，如盐类的分解、含水矿物的脱水、有机质的燃烧等会使物系重量减轻，高温氧化、反应烧结等则会使物系重量增加。

热重分析法(Thermogravimetric Analysis.简称TG) 及微商热重法（derivative thermogravimetry，简称DTG 法）是在程序控制温度下，测量物质质量与温度关系的一种技术。

微商热重法所记录的是TG曲线对温度或时间的一阶导数，所得的曲线称为DTG曲线。

现在的热重分析仪常与微分装置联用，可同时得到TG- DTG曲线。

通过测量物系质量随温度或时间的变化可以间接地揭示固体物系反应的机理和/或反应动力学规律。

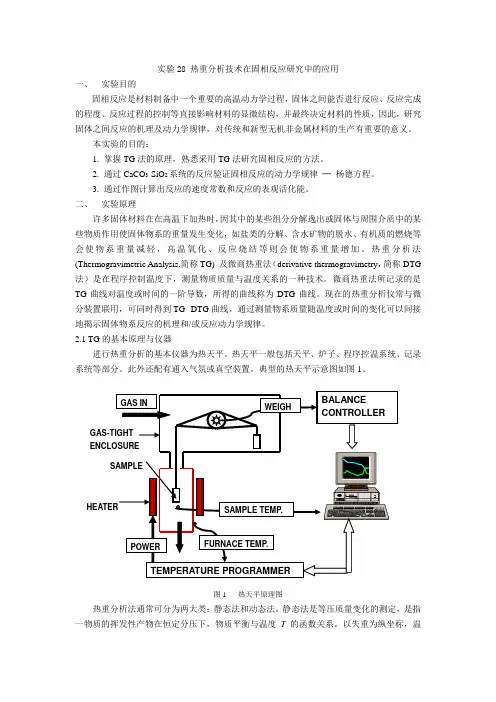
2.1 TG的基本原理与仪器进行热重分析的基本仪器为热天平。

热天平一般包括天平、炉子、程序控温系统、记录系统等部分。

此外还配有通入气氛或真空装置。

典型的热天平示意图如图1。

图1 热天平原理图热重分析法通常可分为两大类：静态法和动态法。

静态法是等压质量变化的测定，是指一物质的挥发性产物在恒定分压下，物质平衡与温度T的函数关系。

以失重为纵坐标，温度T为横坐标作等压质量变化曲线图。

等温质量变化的测定是指一物质在恒温下，物质质量变化与时间t的依赖关系，以质量变化为纵坐标，以时间为横坐标，获得等温质量变化曲线图。

0 0
= ui + RT ( LnN i + Lnγ i )
0
∂ui ∂Lnγ i ) ⇒ = RT (1 + ∂LnN i ∂LnN i
⇒ Di = Bi RT (1 + ∂Lnγ i ) ∂LnN i
Nerst-Einstein方程 方程 或扩散系数的一般热力学方程
理解：
∂ Ln γ 1+ ∂ LnN
∂ ln N i
情况下物质流将由高浓度处流向低浓度处， 情况下物质流将由高浓度处流向低浓度处，扩散的 结果使溶质趋于均匀化。 结果使溶质趋于均匀化。
∂ ln γ i ) < 0 时，Di＜0，称为反常扩散或逆扩散。 ②当 (1 + ，称为反常扩散或逆扩散。 ∂ ln N i
与上述情况相反，扩散结果使溶质偏聚或分相。 与上述情况相反，扩散结果使溶质偏聚或分相。
∆c ∆m ∝ A∆t ∆x
dm ∂c = −D Adt ∂x
∂c J = −D ∂x
→
J = −D ∇ C
→
J 扩散通量，单位时间通过单位截面的质点数(质点数 扩散通量，单位时间通过单位截面的质点数 质点数/s·cm2) 质点数 D 扩散系数，单位浓度梯度的扩散通量 (m2/s 或 cm2/s) 扩散系数， C 质点数/cm3 质点数 “－” 表示粒子从高浓度向低浓度扩散，即逆浓度梯度方向扩散 － 表示粒子从高浓度向低浓度扩散，
2 0 0
讨论： 讨论：
′ ′ （1）高T时，晶体结构中 NV >> N i NV ≈ NV ） 时 扩散为本征缺陷所控制，扩散系数为本征扩散系数 扩散为本征缺陷所控制，扩散系数为本征扩散系数
Q D = D 0 exp( − ) RT

杂质原子、基质原子或缺陷的物质输运过程。
3
从热力学的角度看，只有在绝对零度下才 没有扩散。 通常情况下，对于任何物质来说，不论是 处于哪种聚集态，均能观察到扩散现象：
如气体分子的运动和液体中的布朗运动 都是明显的扩散现象。
4
在固体中，也会发生原子的输运和不断混
合的过程。但是，固体中原子的扩散要比气 体或液体中慢得多。这主要是由于固体中原 子之间有一定的结构和很大的内聚力的原故。 尽管如此，只要固体中的原子或离子分
采用间接非直线间隙扩散。
33
间隙原子的扩散机理势能曲线
间隙原子的势垒如右图
所示：
间隙原子在间隙位置上
处于一个相对的势能极小值，
两个间隙之间存在势能的极
大值，称作势垒（ ）。
间隙原子的势垒
34
通常情况下，间隙原子就在势能极
小值附近作热振动，振动频率 = 1012 ~ 1013 s –1，平均振动能 E kT 。
51
另一方面，由于靠近晶粒间界和 相界面处的结构比内部的结构要松弛
些，这里的原子扩散活化能也要小一
些，大约相当于固体的气化热。
52
这类晶体内部、界面（或表面）的扩散
现象可以用各种实验方法来观察和研究，如 放射性原子示踪、电子探针分析、场离子显 微镜、分割技术等。 例如，借助于分割技术测得了高温下多
布不均匀，存在着浓度梯度，就会产生使浓
度趋向于均匀的定向扩散。
5
二、晶格中原子或离子的扩散过程
1、由于热起伏的存在，晶体中的某些 原子或离子由于剧烈的热振动而脱离格点，
从而进入晶格中的间隙位置或晶体表面，
同时在晶体内部留下空位；
6
2、这些处于间隙位置上的原子或 原格点上留下来的空位，可以从热起

第七章 扩散与固相反应例 题7-1 试分析碳原子在面心立方和体心立方铁八面体空隙间跳跃情况，并以D ＝γr 2Γ形式写出其扩散系数（设点阵常数为a ）。

（式中r 为跃迁自由程；γ为几何因子；Γ为跃迁频率。

）解：在面心立方晶体中，八面体空隙中心在晶胞体心及棱边中心。

相邻空隙连线均为[110]晶向，空隙间距为。

因而碳原子通过在平行的[110]晶面之间跳动完成扩散。

若取[110]为X 轴、]101[为Y 轴、[001]为Z 轴，则碳原子沿这三个轴正反方向跳动的机会相等。

因此碳原子在平行[110]晶面之间跳动的几率即几何因子γ＝1/6。

在体心立方晶体中，八面体空隙中心在晶胞面心及核边中心，相邻空隙间距为a /2。

其连线为[110]晶向，可以认为碳原子通过在平行的[200]晶面之间来完成扩散，取[100]、[010]、[001]为X 、Y 、Z 轴。

碳原子沿这三个轴正反方向跳动机会均等，因而碳原子在平行的[200]晶面间跳动的几率γ＝1/6。

在面心立方铁中2261==r γ代入2D r γ=Γ12)2(6122ΓΓa aD =⨯⨯=面心在体心立方铁中16γ=2r a =24)2(6122ΓΓa a D =⨯⨯=体心7-2 设有一种由等直径的A 、B 原子组成的置换型固溶体。

该固溶体具有简单立方的晶体结构，点阵常数a ＝，且A 原子在固溶体中分布成直线变化，在0.12mm 距离内原子百分数由增至。

又设A 原子跃迁频率Γ＝10-6s -1，试求每秒内通过单位截面的A 原子数解：已知16s 101--⨯=Γ，16γ=；nm 30.==a r ；求扩散通量J 。

s cm 105110)1030(612226372---⨯=⨯⨯⨯==..r D Γγ每cm 3固溶体内所含原子数为322371073)1030(1个⨯=⨯-..2224222421201506337101481000121510148102210s cm ........dc dx J D dc dx ----=⨯⨯=-⨯=-=⨯⨯⨯=⨯7-3 制造晶体管的方法之一是将杂质原子扩散进入半导体材料如硅中。

固相反应法的扩散原理固相反应法是一种常用于合成无机材料的方法，它基于反应物在固体相中的扩散过程，常被用于合成无机材料、合成陶瓷、高温材料和催化剂等。

在固相反应法中，反应物通过扩散在固体相中发生反应，产生所需的产物。

固相反应法的扩散原理可以从多个角度来解释。

以下将从热力学、扩散动力学和固体反应机理三个方面进行讨论。

首先，从热力学角度来看，固相反应需要满足热力学的平衡条件。

这意味着反应混合物组分的化学势之差在反应过程中趋于零。

在固相反应中，反应物分子通过扩散逐渐相互接触，形成局部的处于平衡状态的小区域。

在这些小区域内，反应物由于浓度梯度和局部的温度梯度，会发生反应并释放出能量。

随着时间的推移，反应会逐渐在整个反应体系中进行，直到达到平衡状态。

因此，固相反应法的扩散原理与热力学平衡密切相关。

其次，从扩散动力学的角度来看，固相反应是通过固体颗粒之间的物质迁移实现的。

扩散作为固体相中的质量传递过程，是指物质在固体内部的非均匀分布的自发性移动。

固体颗粒之间存在浓度梯度，质量从梯度高的区域扩散到梯度低的区域。

在固相反应中，反应物的迁移路径通常是由固体颗粒的晶格结构以及物质扩散的速率决定的。

例如，在固相反应法中，反应物粉末的大小、形状和分布对反应速率和产物的物理性质具有显著影响。

因此，固相反应法的扩散原理与物质分子的迁移和扩散速率有关。

最后，从固体反应机理的角度来看，固相反应法是通过反应物的物质转移和相互作用实现的。

在固相反应中，反应物的化学成分从一个相转移到另一个相，进而形成产物。

通常，反应物的转移路径可以分为三个步骤：扩散、表面反应和体相反应。

首先，反应物通过扩散进入固体颗粒相互接触的位置。

然后，在固体颗粒的表面处发生反应，通常是一些中间生成物的生成和反应。

最后，中间生成物会继续在固体内部进行扩散和反应，直到形成所需的产物。

因此，固相反应法的扩散原理与反应物的物质转移和固体表面反应密切相关。

综上所述，固相反应法的扩散原理涉及热力学平衡、扩散动力学和固体反应机理等方面。

内外扩散对气固相催化反应的影响规律篇一：气固相催化反应是指将气体和固体材料之间的反应速率影响因素进行分析和优化,以实现高效的化学反应。

在气固相催化反应中,扩散是一个非常重要的因素,它影响着反应物的传输速率、反应速率和催化剂的寿命等。

本文将介绍气固相催化反应中扩散的影响规律,并探讨如何优化扩散条件以提高催化反应的效率和性能。

一、扩散对气固相催化反应的影响规律1. 扩散系数的影响扩散系数是指物质在两种不同介质之间传输的速率。

在气固相催化反应中,扩散系数取决于物质的相态、温度、压强等因素。

通常情况下,气体分子的扩散系数比固体分子的扩散系数更大,因此在气固相催化反应中,气体分子的扩散速率更快。

2. 温度的影响温度是影响物质扩散的重要因素。

通常情况下,随着温度的升高,扩散系数会减小,这意味着在气固相催化反应中,温度升高会使气体分子的扩散速率更快。

3. 压强的影响压强也是影响物质扩散的重要因素。

通常情况下,随着压强的增大,扩散系数会减小,这意味着在气固相催化反应中,压强增大会使气体分子的扩散速率更快。

4. 物质相态的影响物质相态也会影响扩散速率。

通常情况下,气体分子的扩散速率比固体分子的扩散速率更快。

这是因为气体分子的自由度更大,更容易在固体表面上自由移动。

二、如何优化扩散条件以提高催化反应的效率和性能在气固相催化反应中,优化扩散条件可以提高催化反应的效率和性能。

以下是几种优化扩散条件的方法:1. 选择合适的催化剂和反应条件选择合适的催化剂和反应条件可以优化催化反应的效率和性能。

例如,在选择催化剂时,可以考虑催化剂的活性、选择性、稳定性等因素。

在反应条件方面,可以考虑选择合适的温度、压强、气体浓度等因素。

2. 设计合理的扩散系统设计合理的扩散系统可以提高扩散速率,从而优化催化反应的效率和性能。

例如,可以采用多孔材料、纳米材料等来提高催化剂的表面活性,采用高温高压技术来提高气体分子的扩散速率。

3. 采用合适的添加剂采用合适的添加剂可以提高催化剂的表面积和活性,从而优化催化反应的效率和性能。

扩散与固相反应
扩散与固相反应是材料科学和化学工程等领域的重要研究内容。本课件将详 细介绍扩散与固相反应的定义、特征、影响因素、计算方法、应用等方面的 内容。
扩散
什么是扩散？
分子、离子或原子在固体、液体或气体中沿着 浓度梯度的方向自发移动的现象。
扩散速率的计算方法？
费克定律和斯托克斯-爱因斯坦公式等多种计算 方法。
扩散的影响因素？
浓度梯度、物质性质、温度、压力等因素都会 影响扩散速率。
固相反应
什么是固相反应？
两种或多种固体反应物， 在一定温度和压力下，产 生新的固体产物的反应。
固相反应的速率计算？
固相反应的影响因？
固相反应速率受物质传递 速率、反应速度常数等因 素影响，可以通过动力学 方程计算。
温度、反应物浓度、反应 物粒度等都会影响固相反 应的速率。
将越来越多地应用在材料、化学、环保、电子、航空等多个领域，具有广阔的应用前景。
扩散与固相反应的关系
1
扩散与固相反应的相互作用？
扩散过程参与反应运动和物质传递，
扩散对反应速率的影响？
2
对固相反应的进行有重要影响。
扩散控制下的固相反应速率与扩散速
率成正比，是反应速率的主要控制因 素。
3
扩散控制下的固相反应？
扩散控制下的固相反应特点是固体表 面存在浓度梯度，因此其速率与扩散 速率相关。
实际应用
扩散与固相反应在材料科学中的应用？
半导体器件制造、新材料合成等领域。
扩散与固相反应在化学工程中的应用？
催化剂制备、化学反应等领域。
总结与展望
扩散与固相反应的研究现状？
是材料科学、化学工程等领域重要研究方向之一，研究方向包括反应机理、动力学行为、影 响因素等。

稳定扩散： 若扩散物质在扩散层dx内各处的浓度不随时间
而变，即 dc 0 ，这种扩散是稳定扩散。
dt
不稳定扩散： 扩散物质在扩散层dx内的浓度随时间而变化
即 dc 0，为不稳定扩散。
dt
1. 菲克定律
第一定律：
内容：若扩散介质中存在着扩散物质的浓度差， 在此浓度的推动下产生沿浓度减少方向的定向扩 散。当扩散为稳定扩散时，在dt（s）时间内，通 过垂直于扩散方向平面上的ds（m2）面积的扩散 流量（质点数目）与沿扩散方向上的浓度梯度成 正比。
C(x,t) C0 (1
2 ) e 2 d 0
引入误差函数的余误差函数概念：
erf ( ) 2 e 2 d
0
erfc( ) 1 2 e 2 d
0
C(x,t) C0 erfc(x 2 Dt )
erfc( )可由误差函数表查得

N
I
)
exp
S M
R
exp
H M
RT

讨论：
1.当温度足够高时，N
' V

NI
，此时扩散为本征扩散
控制：
Q H f 2 H M

D0
a0 20
exp S f
2 R
S M

2.当温度足够低时，
N
' V
i Ci

C Ni , d ln Ci
Bi
i ln Ci
d ln Ni



Di

Bi

i ln Ni

i


0 i

第七章扩散与固相反应§7-1 晶体中扩散的基本特点与宏观动力学方程一、基本特点1、固体中明显的质点扩散常开始于较高的温度，但实际上又往往低于固体的熔点；2、晶体中质点扩散往往具有各向异性，扩散速率远低于流体中的情况。

二、扩散动力学方程1、稳定扩散和不稳定扩散在晶体A中如果存在一组分B的浓度差，则该组分将沿着浓度减少的方向扩散，晶体A作为扩散介质存在，而组分B则为扩散物质。

如图，图中dx为扩散介质中垂直于扩散方向x的一薄层，在dx两侧，扩散物质的浓度分别为c1和c2，且c1＞c2，扩散物质在扩散介质中浓度分布位置是x的函数，扩散物质将在浓度梯度的推动下沿x方向扩散。

的浓度分布不随时间变的扩散过程稳定扩散：若扩散物质在扩散层dx内各处的浓度不随时间而变化，即dc/dt=0。

这种扩散称稳定扩散。

不稳定扩散：扩散物质在扩散层dx内的浓度随时间而变化，即dc/dt≠0。

这种扩散称为不稳定扩散。

2、菲克定律（1）菲克第一定律在扩散体系中，参与扩散质点的浓度因位置而异，且随时间而变化，即浓度是坐标x、y、z和时间t函数，在扩散过程中，单位时间内通过单位横截面积的质点数目（或称扩散流量密度）j之比于扩散质点的浓度梯度△cD：扩散系数；其量纲为L2T-1，单位m2/s。

负号表示粒子从浓度高处向浓度低处扩散，即逆浓度梯度的方向扩散，对于一般非立方对称结构晶体，扩散系数D为二阶张量，上式可写为：对于大部分的玻璃或各向同性的多晶陶瓷材料，可认为扩散系数D将与扩散方向无关而为一标量。

J x=-D J x----沿x方向的扩散流量密度J y=-D J y---沿Y方向的扩散流量密度J z=-D J z---沿Z方向的扩散流量密度适用于：稳定扩散。

菲克第二定律：是在菲克第一定律基础上推导出来的。

如图所示扩散体系中任一体积元dxdydz在dt时间内由x方向流进的净物质增量应为：同理在y、z方向流进的净物质增量分别为：放在δt时间内整个体积元中物质净增量为：若在δt时间内，体积元中质点浓度平均增量δc，则：若假设扩散体系具有各向同性，且扩散系数D不随位置坐标变化则有：适用范围：不稳定扩散。

第七章 扩散与固相反应内容提要：晶体中原子（离子）的扩散是固态传质和反应等过程的基础。

本章讨论了扩散的两个问题。

一是扩散现象的宏观规律——菲克第一、第二定律，描述扩散物质的浓度分布与距离、时间的关系。

二是扩散微观机制，即扩散过程中原子迁移的方式。

在了解原子移动规律的基础上讨论了固相反应的扩散动力学方程。

杨德尔与金斯特林格方程的推导及其适用的范围。

简要介绍了影响固相反应的因素。

固体中质点（原子或离子）的扩散特点：固体质点之间作用力较强，开始扩散温度较高，但低于其熔点；晶体中质点以一定方式堆积，质点迁移必须越过势垒，扩散速率较低，迁移自由程约为晶格常数大小；晶体中质点扩散有各向异性。

菲克第一定律：在扩散过程中，单位时间内通过单位截面的质点数目（或称扩散流量密度）J 正比于扩散质点的浓度梯度c :)(zc k y c j x c i D D ∂∂+∂∂+∂∂-=∇-= 式中D 为扩散系数s m 2或s cm 2；负号表示粒子从浓度高处向浓度低处扩散，即逆浓度梯度的方向扩散。

菲克第一定律是质点扩散定量描述的基本方程，它可直接用于求解扩散质点浓度分布不随时间变化的稳定扩散问题。

菲克第二定律适用于求解扩散质点浓度分布随时间和距离而变化的不稳定扩散问题。

)(222222zc y c x c D t c ∂∂+∂∂+∂∂=∂∂ 扩散过程推动力是化学位梯度。

物质从高化学位流向低化学位是一普遍规律。

扩散系数的一般热力学关系式：)ln ln 1(i i i i N RTB D ∂∂+=γ式中i D 为i 质点本征扩散系数；i B 为i 质点平均速率或称淌度；i γ为i 质点活度系数；i N 为i 质点浓度。

)ln ln 1(i i N ∂∂+γ称为扩散系数的热力学因子。

当体系为理想混合时1=i γ，此时i i i RTB D D ==*。

*i D 为自扩散系数。

当体系为非理想混合时，有两种情况：（1）当0)ln ln 1(>∂∂+i i N γ，0>i D 为正扩散。