数理统计11判别分析
- 格式:ppt
- 大小:1.75 MB
- 文档页数:64






判别分析方法及其应用效果评估判别分析方法是一种常用的统计分析方法,用于确定分类系统中哪些变量最能有效地区分不同的组别。
它基于一组预测变量(或称为自变量)的输入值,以及一组已知类别(或称为因变量)的输出值,通过构建分类模型来判断新样本属于哪个组别。
本文将介绍判别分析方法的基本原理、常见的判别分析方法及其应用效果评估。
## 一、判别分析方法的基本原理判别分析方法基于贝叶斯决策理论,旨在通过最小化错判率来实现最优分类。
假设有K个已知的类别,以及p个预测变量。
判别分析方法假设预测变量满足多元正态分布,并利用已知类别的样本数据估计每个类别的均值向量和协方差矩阵。
根据这些参数,可以建立判别函数来判断新样本的分类。
判别函数的形式根据具体的判别分析方法而定。
常见的判别分析方法有线性判别分析(LDA)、二次判别分析(QDA)和最近邻判别分析(KNN)等。
这些方法使用不同的数学模型和算法来构建判别函数,具有不同的优势和适用范围。
## 二、常见的判别分析方法及其特点### 1. 线性判别分析(LDA)线性判别分析是一种最常用的判别分析方法。
它假设各类别的协方差矩阵相等,即样本来自同一多元正态分布。
LDA通过计算类别间散布矩阵和类别内散布矩阵的比值来确定最优的判别函数。
LDA的优点是计算简单、效果稳定,并且不受样本数量和维度的限制。
然而,它对样本的分布假设要求较高,如果样本不满足多元正态分布,LDA可能会出现较大偏差。
### 2. 二次判别分析(QDA)二次判别分析是一种放宽了协方差矩阵相等假设的判别分析方法。
QDA假设每个类别的协方差矩阵各不相同,通过计算类别间散布矩阵和类别内散布矩阵的比值来确定最优的判别函数。
相比于LDA,QDA更加灵活,可以适应更加复杂的数据分布。
然而,由于需要估计更多的参数,QDA的计算复杂度较高,并且对样本数量和维度的要求较高。
### 3. 最近邻判别分析(KNN)最近邻判别分析是一种基于样本距离的判别分析方法。

判别分析的基本原理和模型一、判别分析概述 (一)什么是判别分析判别分析是多元统计中用于判别样品所属类型的一种统计分析方法,是一种在已知研究对象用某种方法已经分成若干类的情况下,确定新的样品属于哪一类的多元统计分析方法。
判别分析方法处理问题时,通常要给出用来衡量新样品与各已知组别的接近程度的指标,即判别函数,同时也指定一种判别准则,借以判定新样品的归属。
所谓判别准则是用于衡量新样品与各已知组别接近程度的理论依据和方法准则。
常用的有,距离准则、Fisher 准则、贝叶斯准则等。
判别准则可以是统计性的,如决定新样品所属类别时用到数理统计的显著性检验,也可以是确定性的,如决定样品归属时,只考虑判别函数值的大小。
判别函数是指基于一定的判别准则计算出的用于衡量新样品与各已知组别接近程度的函数式或描述指标。
(二)判别分析的种类按照判别组数划分有两组判别分析和多组判别分析;按照区分不同总体的所用数学模型来分有线性判别分析和非线性判别分析;按照处理变量的方法不同有逐步判别、序贯判别等;按照判别准则来分有距离准则、费舍准则与贝叶斯判别准则。
二、判别分析方法 (一)距离判别法1.基本思想:首先根据已知分类的数据,分别计算各类的重心,即分组(类)均值,距离判别准则是对于任给一新样品的观测值,若它与第i 类的重心距离最近,就认为它来自第i 类。
因此,距离判别法又称为最邻近方法(nearest neighbor method )。
距离判别法对各类总体的分布没有特定的要求,适用于任意分布的资料。
2.两组距离判别两组距离判别的基本原理。
设有两组总体B A G G 和,相应抽出样品个数为21,n n ,n n n =+)(21,每个样品观测p 个指标得观测数据如下,总体A G 的样本数据为:()()()()()()()()()A x A x A x A x A x A x A x A x A x p n n n p p 111212222111211ΛΛMΛΛΛΛ该总体的样本指标平均值为:()()()A x A x A x p Λ21,总体B G 的样本数据为:()()()()()()()()()B x B x B x B x B x B x B x B x B x p n n n p p 222212222111211ΛΛMΛΛΛΛ该总体的样本指标平均值为:()()()B x B x B x p Λ21,现任取一个新样品X ,实测指标数值为X =(p x x x ,,,21Λ),要求判断X 属于哪一类?首先计算样品X 与A G 、B G 两类的距离,分别记为()A G X D ,、()B G X D ,,然后按照距离最近准则判别归类,即样品距离哪一类最近就判为哪一类;如果样品距离两类的距离相同,则暂不归类。

第11,12,13课判别分析(Discriminant Analysis)讲五个问题:一、什么是判别分析;二、费歇准则下的二组判别分析;三、贝叶斯多组判别分析;四、多组逐步判别分析;五、问题讨论和实例。
一、什么是判别分析概念:判别分析是一种判别样品所属类型的统计方法。
思想:根据已知类型的样品,按其特征,构造一个判别函数,定出划分类型的界线,并对新样品所属类型进行判别(也可对已知类型的样品进行判别检验)。
类型:若判别类型是两个时,称两组判别分析。
如油层、水层;有矿、无矿等。
若判别的类型是两个以上时称多组判别分析。
如油层、气层、水层;泥岩、砂岩、灰岩等。
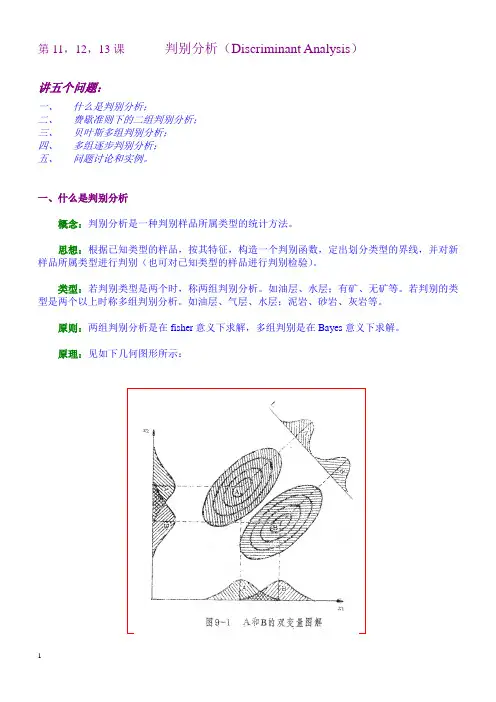
原则:两组判别分析是在fisher意义下求解,多组判别是在Bayes意义下求解。
原理:见如下几何图形所示:当P=2时:211221jjj y c x c x cx ==+=∑当在P 维时:11221pp p jj j y c x c x c x cx ==+++=∑y—综合指标,是i x 的线性函数,也有非线性的。
式中:j c —判别系数。
应用:◆ 判别和检验样品的所属类型;◆评价,如岩体评价,区别海相或陆相砂岩,区别含油层或含水层。
鉴别矿物、岩石类型和古生物的种属;◆地层和岩相的划分;◆解释砂体的构造背景,区别沉积条件和环境,火山构造类型等。
二、两组判别分析—Fisher 准则前提条件:A 、B 两类总体,A 组取了1n 个样品,B 组取了2n 个样品,每个样品测定了P 个指标,原始数据见教材。
1、求线性判别函数y11221pp p jj j y c x c x c x cx ==+++=∑式中:j c —待定系数 j x —指标问题的关键是如何求得j c ,使得A 、B 两组分的很清楚,即要得到y 值,使得A 、B 区分开。
原则:Fisher :类间差别要大,类内差别要小。
综合指标 A 类 (1n 个样品) 综合指标 B 类 (2n 个样品)1112121222(),(),,()(),(),,()P P x A x A x A x A x A x A 12()()y A y A 1112121222(),(),,()(),(),,()P P x B x B x B x B x B x B 12()()y B y BA 类样品用 1111()()n i i y A y A n ==∑——代表=1()()pjj j y A cx A ==∑A 类样品用 2121()()n i i y B y B n ==∑——代表=1()()pjj j y B cx B ==∑A 类内差别为:[]121()()n i i y A y A =-∑B 类内差别为:[]221()()n i i y B y B =-∑类内差别为:[][]122211()()()()n n iii i F y A y A y B y B ===-+-∑∑类间差别为:[]2()()Q y A y B =-Fisher 准则:使Q I F=达到极大,求出j c 。

第9章判别分析判别分析是一种常用的统计分析方法。
判别分析是根据观察或测量到若干变量值,判断研究对象如何分类的方法。
例如,我们积累了某种病虫害各种发生状态的若干历史资料样本),希望从中总结出分类的规律性(即判别公式,在以后的工作中遇到新的发生状态(样本)时。
只要根据总结出来的判别公式判断它所属的类就行了。
动物、植物分类等都可以用判别分析来解决。
进行判别分析必须已知观测对象的分类和若干表明观测对象特征的变量值。
判别分析就是要从中筛选出能提供较多信息的变量并建立判别函数,使得利用推导出的判别函数对观测量判别其所属类别时的错判率最小。
判别函数一般形式是: Y = a1X1+a2X2+a3X3...+a n X n其中: Y为判别分数(判别值);X1,X2,X3:…Xn为反映研究对象特征的变量,a1、a2、a3…an为各变量的系数,也称判别系数。
可以看出我们这里所讲的是线性判别函数。
SPSS 对于分为m类的研究对象,建立m个线性判别函数。
对于每个个体进行判别时,把测试的各变量值代入判别函数,得出判别分数,从而确定该个体属于哪一类。
或者计算属于各类的概率,从而判断该个体属于哪—类。
还可建立标准化和未标准化的典则判别函数。
SPSS提供的判别分析过程是Discriminant过程。
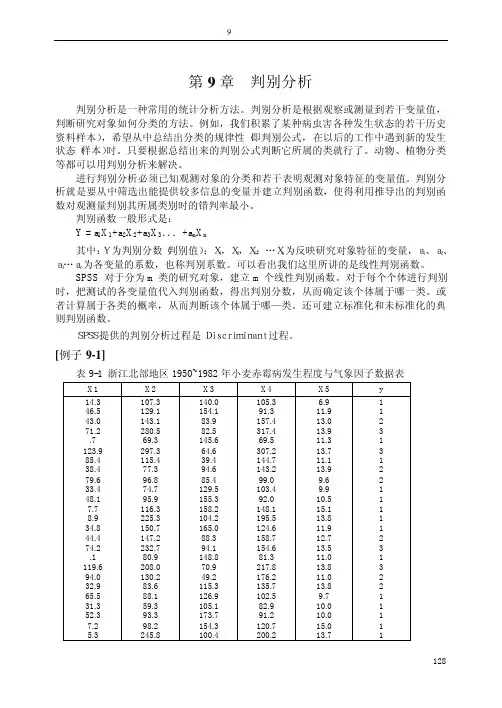
[例子9-1]表9-1 浙江北部地区1950~1982年小麦赤霉病发生程度与气象因子数据表X1 X2 X3 X4 X5 y14.3 107.3 140.0 105.3 6.9 146.5 129.1 154.1 91.3 11.9 143.0 143.1 83.9 157.4 13.0 271.2 280.5 82.5 317.4 13.9 3.7 69.3 145.6 69.5 11.3 1123.9 297.3 64.6 307.2 13.7 385.4 115.4 39.4 144.7 11.1 138.4 77.3 94.6 143.2 13.9 279.6 96.8 85.4 99.0 9.6 233.4 74.7 129.5 103.4 9.9 148.1 95.9 155.3 92.0 10.5 17.7 116.3 158.2 148.1 15.1 18.9 225.3 104.2 195.5 13.8 134.8 150.7 165.0 124.6 11.9 144.4 147.2 88.3 158.7 12.7 274.2 232.7 94.1 154.6 13.5 3.1 80.9 148.8 81.3 11.0 1119.6 208.0 70.9 217.8 13.8 394.0 130.2 49.2 176.2 11.0 232.9 83.6 115.3 135.7 13.8 265.5 88.1 126.9 102.5 9.7 131.3 59.3 105.1 82.9 10.0 152.3 93.3 173.7 91.2 10.0 17.2 98.2 154.3 120.7 15.0 15.3 245.8 100.4 200.2 13.7 1128129浙江北部地区1950~1982年小麦赤霉病发生程度与气象因子研究,总结出上年12月将与(x1)、上年10月下旬至11月中旬和当年1~2月总降雨(x2)、上年10月下旬至11月上旬日照时数(x3)、上年10月下旬至12月中旬和当年2月总雨量(x4)以及当年3月中旬平均高文(x5)等5个因子,并将赤霉病情分为轻中重三级(y ,分别用1、2、3表示)。
判别分析判别分析是一种常用的统计分析方法,根据观察或测量到若干变量值,判别研究对象属于哪一类的方法。
进行判别分析必须已知观测对象的分类和若干表明观测对象特征的变量值。
判别分析就是要从中筛选出能提供较多信息的变量并建立判别函数,使得利用推导出的判别函数对观测量判别其所属类别时的错判率最小。
线性判别函数一般形式是1122...n n y a x a x a x =+++,y 为判别分数(判别值),n x 为反映研究对象特征的变量,n a 为各变量的判别系数。
典则判别分析:建立典则变量代替原始数据文件中指定的自变量。
典则变量是原始自变量的线性组合。
用少量的典则变量代替原始的多个变量可以比较方便地描述各类之间的关系。
实验:实验数据见:判别分析2010.sav .例1:一个城市的居民家庭,按其有无割草机可分为两组,有割草机的记为一组为1π,没有割草机的一组记为2π,割草机工厂欲判断一些家庭是否购买割草机。
从1π和2π分别随机抽取12个样品,调查两项指标:1x =家庭收入,2x =房前屋后土地面积。
用y 作为二元被解释变量,有割草机的家庭用1表示,没有割草机的家庭用0表示,12,x x 作为解释变量。
实验步骤:打开判别分析2010.sav ,之后选择判别分析。
选择变量,定义范围分组变量:必须是离散变量,设置分类变量的范围选择变量:选择一部分符合条件的观测量进行判别函数的推导,而且有一个变量的某个值可以作为这些观测量的标识。
例如:新设一个变量group,选择group=1,则只有group=1的观测量参与判别函数的推导。
一起输入自变量:判别分析过程使用所有的自变量进行判别分析,建立全模型。
使用步进式方法:筛选能对观测量的特性提供丰富的信息的自变量进入判别分析。
在“方法”栏中作相应选择Wilks’lambda:每步都是Wilk的lambda统计量最小的进入判别函数。
未解释方差:每步都是各类不可解释的方差和最小的变量进入判别函数。
数据分析知识:数据分析中的判别分析方法判别分析是一种统计分析方法,用于确定一个或多个自变量对于分类变量的影响程度。
它主要用于识别和定量分析不同群体之间的差异,从而帮助人们做出正确的判断和决策。
判别分析方法在许多不同领域都有着广泛的应用,包括市场营销、医学、社会科学等。
在进行判别分析之前,首先需要明确分类变量和自变量的关系。
分类变量是研究对象的属性,例如不同的产品类型、疾病种类、用户群体等;自变量则是用来解释分类变量的因素,可包括多种属性或指标。
判别分析的目标是通过自变量来识别分类变量的不同群体,并且量化它们的差异程度。
判别分析的基本原理是利用自变量对不同分类变量进行分类和区分。
在进行判别分析时,需要建立一个判别函数,用来预测或计算分类变量的概率。
这个判别函数可以是线性的,也可以是非线性的,具体的形式取决于研究对象和数据特点。
判别函数的建立需要借助统计模型和算法,例如线性判别分析(LDA)、逻辑回归、支持向量机等。
这些方法都是在不同的数学理论和假设基础上发展起来的,具有各自的适用场景和特点。
在实际应用中,判别分析可以帮助人们识别和解释分类变量的差异。
举个例子,假如我们想要研究不同用户群体对于某个产品的偏好程度,我们可以收集用户的属性信息(如年龄、性别、收入等)作为自变量,产品的满意度(比如评分或者购买意愿)作为分类变量。
通过判别分析,我们可以分析出不同群体之间的偏好差异,找出对产品偏好影响最大的因素,从而为产品营销和推广提供科学依据。
在医学领域,判别分析也有着重要的应用价值。
例如,我们可以利用病人的临床指标(如血压、血糖、血脂等)作为自变量,疾病的种类(如高血压、糖尿病、心血管疾病等)作为分类变量,通过判别分析来识别不同疾病之间的特征和差异,帮助医生进行疾病诊断和治疗。
在社会科学领域,判别分析也常常用于对不同人群的心理特征和行为模式进行分类和分析。
比如,通过收集人们的性格特征、消费行为、社交习惯等自变量,可以对他们进行分类并识别出不同群体之间的差异,从而更好地理解和预测人的行为和决策。