切线长定理(用)

切线长定理内容切线长定理是微积分中的一个基本定理,它描述了一条切线的长与其斜率之间的关系。

切线长定理的内容如下:设 $f(x)$ 是 $n$ 维区间 $(a,b)$ 上的一个可导函数,$g(x)$ 是 $n$ 维向量,则对于任意的 $c in (a,b)$,都有:$$frac{f(b) - f(a)}{g(b) - g(a)} =frac{d}{dx}left(frac{f"(x)}{f(x)}g(x)ight)$$其中,$f"(x)$ 是 $f(x)$ 在 $x$ 处的导数,$g(x)$ 的斜率。

这个定理的表述比较简单,但其证明需要一些高等数学的知识。

下面给出一个简单的证明:首先,可以证明 $f(x)$ 在 $x=a$ 和 $x=b$ 处的函数值相等: $$f(a) = f(b)$$然后,假设 $c in (a,b)$,则有:$$frac{f(b) - f(a)}{g(b) - g(a)} =frac{d}{dx}left(frac{f"(x)}{f(x)}g(x)ight)将 $f(a)$ 和 $f(b)$ 带入得:$$frac{f(b) - f(a)}{g(b) - g(a)} = frac{f"(c)}{f(c)}g(c) $$由于 $g(x)$ 在 $x=c$ 处是已知的,因此有:$$frac{f(b) - f(a)}{g(b) - g(a)} = frac{f"(c)}{f(c)}$$将 $f"(x)$ 的导数代入得:$$frac{f(b) - f(a)}{g(b) - g(a)} = frac{f"(c)}{f(c)}g(c) = frac{f"(c)}{f(c)} frac{f"(b)}{f(b)} frac{f(b) - f(a)}{f(b) - f(a)}$$由于 $g(x)$ 在 $x=c$ 处是已知的,因此有:$$frac{f"(b)}{f(b)} frac{f(b) - f(a)}{f(b) - f(a)} =frac{f"(c)}{f(c)}$$根据定义,有 $f"(x)$ 和 $g(x)$ 在 $x=c$ 处的值相等,因此有:frac{f"(b)}{f(b)} = frac{f"(c)}{f(c)}$$又因为 $f"(x)$ 是 $f(x)$ 在 $x$ 处的导数,所以有:$$f"(c) = f"(b) = f"(a) = 0$$由于 $f(x)$ 在 $x=a$ 和 $x=b$ 处的函数值相等,因此有: $$f(b) - f(a) = f"(c)(f(b) - f(a)) = 0$$将其代入上式得:$$frac{f(b) - f(a)}{g(b) - g(a)} = frac{f"(c)}{f(c)} $$因此,根据切线长定理,有:$$frac{f(b) - f(a)}{g(b) - g(a)} = frac{f"(c)}{f(c)} $$即:$$frac{f"(x)}{f(x)} =frac{d}{dx}left(frac{f"(x)}{f(x)}g(x) ight)$$因此,切线长定理成立。

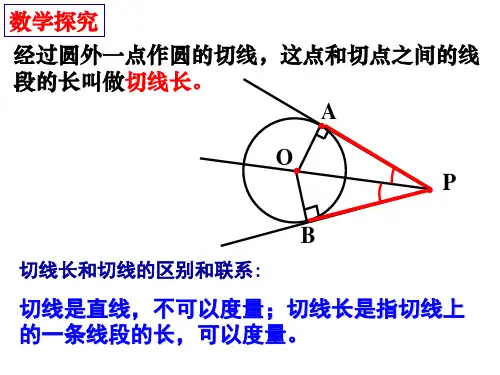
切线长定理及其应用知识点一 切线长定义及切线长定理1. 切线长定义：过圆外一点作圆的切线，这点和 之间的线段长叫作这点到圆的切线长.注意切线长和切线的区别和联系:切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量。

2. 切线长定理：过圆外一点引圆的两条切线，它们的切线长相等，即PA=PB.推论：（1）△PAB 是等腰三角形；（2）OP 平分△APB ，即△APO=△BPO ；（3）弧AM=弧BM ；（4）在Rt OAP ∆和Rt OBP ∆中，由AB OP ⊥，可通过相似得相关结论；如：222222,,OA OB OE OP AP BP PE PO AE BE OE EP ==⋅==⋅==⋅（5）图中全等的三角形有对，分别是：题型一 切线长定理的直接应用【例1】如图所示，△O 的半径为3cm ，点P 和圆心O 的距离为6cm ，经过点P 的两条切线与△O 切于点E 、F ，求这两条切线的夹角及切线长.【例2】如图，P A 、PB 、DE 分别切△O 于A 、B 、C ，△O 的半径长为6 cm ，PO ＝10 cm ，求△PDE 的周长．【例3】如图所示，△ABC中，∠C=90°，AC=3，AB=5，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为__________.【过关练习】1.如图所示，PA、PB是△O的切线，A、B为切点，△OAB=30°.（1）求△APB的度数.（2）当OA=3时，求AP的长.2.如图所示，已知PA、PB、DE分别切O于A、B、C三点，△O的半径为5cm，△PED的周长为24cm，△APB=50°.求：（1）PO的长；（2）△EOD的度数.3.如图,在直角梯形ABCD 中,AB ∥CD,AB ⊥BC,以BC 为直径的△O 与AD 相切,点E 为AD 的中点,下列结论正确的个数是( )(1)AB+CD=AD;(2)DCE ABE BCE S S S △△△+=; (3)241BC CD AB =⋅; (4)∠ABE=∠DCE. A.1B.2C.3D.4知识点二 圆外切四边形1、四边形的内切圆定义：四边形的四条边都与圆相切，把这个四边形叫作圆外切四边形，把这个圆叫作圆的内切圆.2、圆外切四边形的性质：圆外切四边形两组对边之和.（如图，即AB +CD =AD +BC ） 题型一 四边形的内切圆计算【例1】已知四边形ABCD 的边AB 、BC 、CD 、DA 与△O 相切于P 、Q 、M 、N ，求证：AB+CD=AD+BC 。

切线长定理逐字稿切线长定理是指在任一曲线上，任一点的切线的斜率与曲线的斜率的乘积等于曲线的弧长。

性质：1、曲线的曲线弧长与点的切线斜率成正比；2、某点的切线斜率与曲线的曲线弧长之差的绝对值最小；3、曲线的曲线弧长与曲线的斜率成正比；4、某点的切线斜率与曲线的曲线弧长之和的绝对值最大；5、某点的切线斜率越大，则该点弧长与曲线斜率成正比的关系越紧密；6、某点的切线斜率越小，则该点弧长与曲线斜率成正比的关系越松散。

应用：1、切线长定理用于计算弧线和曲线的曲线长度，当知道切线的斜率时，可以计算出曲线的曲线长度；2、切线长定理也可以用来判断不同的函数的性质，以及求解几何函数的特征；3、切线长定理也可以用于最优路径问题，在建立求解曲线最优路径的具体方案时，可以利用切线长定理对路径进行优化；4、切线长定理也可用于积分的求解，求解不同曲线的面积，当知道切线的斜率时，可以使用此定理计算曲线的面积。

证明：假设曲线是由x=(x,y§)的函数表示的曲线，考虑曲线上的关于曲线的某一点P，取准点O和P之间的短线段OP，假设其切线斜率为K，曲线的斜率为k，那么在点P处我们可以构造一条和切线在P点重合的矢量，用差分公式表示为begin{equation}Delta x=(Delta x,Deltay)=(x_{2}-x_{1},y_{2}-y_{1})=KcdotDelta send{equation} 将差分公式代入到函数中并做微积分，便得到begin{equation}int_{P_{1}}^{P_{2}}KDeltasds=int_{P_{1}}^{P_{2}}left(f^{prime}(x)right)Delta xdxend{equation}即begin{equation}Kcdotint_{P_{1}}^{P_{2}}Deltasds=int_{P_{1}}^{P_{2}}left(f^{prime}(x)right)Delta xdxend{equation}由上述公式可以知道，切线斜率K和曲线斜率k之间的乘积等于曲线的曲线弧长，即begin{equation}Kcdot k=int_{P_{1}}^{P_{2}}Delta sdsend{equation}这就是切线长定理的证明。

专题9 巧用切线长定理解题【知识解读】切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，并且这点和圆心的连线平分两条切线的夹角.该定理在计算和证明中应用相当广泛，常常可用来解决以下几种题型：①求角度；②求线段长；③证线段相等；④证明线段成比例；⑤证明线段平行；⑥与三角形内切圆有关的问题.培优学案【典例示范】例1 已知⊙0的两条切线P A和PB相交于点P，与⊙0相切于A，B两点，C是⊙O上的一点，若∠P= 60°，求∠ACB的度数.【提示】由于点C的位置不确定，所以需要分类讨论.【解答】【跟踪训练】如图1-9-1，CA和CB都是⊙O的切线，切点分别是A，B，如果⊙O的半径为23，且AB=6，求∠ACB的度数.【解答】OC BA例2 如图1-9-2①，△ABC中，CA=CB，点O在高CH上，OD⊥CA于点D，OE⊥CB于点E，以O 为圆心，OD为半径作⊙O.（1）求证：⊙O与CB相切于点E；（2）如图1-9-2②，若⊙O过点H，且AC=5，AB=6，连接EH，求△BHE的面积.【提示】（1）由等腰三角形的性质易得CH是∠ACB的平分线，再根据角平分线的性质定理得OE=OD，即圆心O到直线CB的距离等于半径，所以结论得证；（2）先由等腰三角形的性质，得BC=AC=5，BH=AH=3，在Rt△BCH中，由勾股定理得CH=4；再由切线长定理得BE=BH=3；然后，过点E作EF⊥AB于点F，则易得△BEF∽△BCH，根据相似三角形的对应边成比例得EF的长，则△BHE的面积=12BH·EF.图1-8-20EOHDBOHEDCB【解答】【跟踪训练】如图1-9-3，在△ABC 中，∠ABC =90°，0是AB 上的一点，以O 为圆心，OB 为半径的圆与AB 交于点E ，与AC 切于点D ，连接DB ，DE ，OC ，若AD =2，AE =1，求CD 的长.【解答】OEDCBA例3 如图1-9-4，P A ，PB 切⊙0于A ，B 两点.CD 切⊙0于点E ，交P A ，PB 于C ，D ，若⊙O 的半径为r ，△PCD 的周长等于3r ，则tan ∠APB 的值是 （ ） A.51312 B. 125 C. 3135D.2133 【提示】先利用切线长定理将△PCD 的周长转化成线段P A 长的2倍，构造出切线长定理的基本图形，利用勾股定理、面积法或者是三角函数计算出相关线段的长度，最后将所求的∠APB 放在一个直角三角形中，将它的正切值转化为两条线段的比值即可得到答案.图1-9-2①图1-9-2②图1-9-3OE DCBAPDCBA【跟踪训练】如图1-9-5，⊙A 与⊙B 外切于点D ，PC ，PD ，PE 分别是圆的切线，C ，D ，E 是切点，若∠CED =°，∠ECD =y °，⊙B 的半径为R ，则DE ︵的长度是 （ ）A.(90)90x Rπ- B.(90)90y Rπ- C.(180)180x Rπ- D.(180)180y Rπ-例4 如图1-9-6①所示，AB 为⊙O 的直径，AD 与⊙0相切于点A ，DE 与⊙O 相切于点E ，点C 为DE 延长线上一点，且CE =CB .（1）求证：BC 为⊙O 的切线；（2）连接AE ，AE 的延长线与BC 的延长线交于点G （如图②所示）.若AB =25，AD =2，求线段BC 和EG 的长. 【提示】（1）欲证明BC 为⊙O 的切线，依据切线的判定定理，需证明OB ⊥BC ，为此要连接OC ，OE ，设法证明△OBC ≌△OEC ，得∠0BC =∠OEC =90°；（2）需顺着（1）问结论，灵活运用切线长定理，勾股定理，相似三角形知识解答，关键有二：一连接BE ，发现EC =BC =CG ；二通过过点D 作BG 边上的高构造直角三角形，应用勾股定理求出CE 的长。

知识点一切线长定义及切线长定理1. _____________________________________________________ 切线长定义：过圆外一点作圆的切线，这点和____________________________________________ 之间的线段长叫作这点到圆的切线长注意切线长和切线的区别和联系：切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量。

2. 切线长定理：过圆外一点引圆的两条切线，它们的切线长相等，即PA=PB.推论:(1) △ PAB是等腰三角形；(2) OP 平分△ APB，即△ APO A BPO ；(3) 弧AM=弧BM ;(4)在Rt OAP和Rt OBP中，由AB OP，可通过相似得相关结论;如：OA2 OB2 OE OP, AP2 BP2 PE PO, AE2 BE2 OE EP(5)图中全等的三角形有对，分别是：题型一切线长定理的直接应用【例1】如图所示，AO的半径为3cm,点P和圆心O的距离为6cm,经过点P的两条切线与AO切于点E、F,求这两条切线的夹角及切线长.【例2】如图，FA、PB、DE分别切A0于A、B、C, A O的半径长为6 cm, PO= 10 cm,求APDE的周长.切线长定理及其应用【例3】如图所示，△ ABC中，/ C=90 , AC=3 , AB=5 , D为BC边的中点，以AD上一点0为圆心的O0和AB、BC均相切，则O 0的半径为 ______________ .£4【过关练习】1•如图所示，PA、PB是AO的切线，A、B为切点，△ OAB=30°.( 1)求厶APB的度数.(2)当0A=3时,求AP的长•2•如图所示，已知PA、PB、DE分别切e 0于A、B、C三点，AO的半径为5cm, △ PED的周长为24cm , △ APB=50°求：(1) P0 的长；(2) △ EOD 的度数•3•如图，在直角梯形 ABCD 中,AB // CD,AB 丄BC,以BC 为直径的 △ 与AD 相切，点E 为AD 的中点，下列结论 正确的个数是( )B1 2知识点二圆外切四边形1、四边形的内切圆定义：四边形的四条边都与圆相切，把这个四边形叫作圆外切四边形，把这个圆叫作圆的内切圆2、圆外切四边形的性质：圆外切四边形两组对边之和 __________________ .（如图，即AB+CD=AD+BC ）题型一 四边形的内切圆计算【例1】已知四边形 ABCD 的边AB 、BC 、CD 、DA 与AO 相切于P 、Q 、M 、N ，求证：AB+CD=AD+BC 。

圆的切线长定理及其推论一、引言圆是数学中重要的几何概念之一，它具有许多独特的性质和定理。

本文将重点介绍圆的切线长定理及其推论，通过详细的阐述和推导，帮助读者更好地理解和应用这一定理。

二、圆的切线长定理圆的切线长定理是指：若直线与圆相切，则切线的长度等于切点到圆心的距离的平方根乘以2。

证明：设圆的方程为x²+y²=r²，其中r为圆的半径，切点为P(x₀, y₀)。

设直线方程为y=kx+b，其中k为斜率，b为截距。

由于直线与圆相切，所以切点的坐标满足直线方程和圆的方程，即有：kx₀+b=y₀x₀²+y₀²=r²将直线方程中的y用x和b表示，代入圆的方程，得到：x²+(kx+b)²=r²化简得：(1+k²)x²+2kbx+b²-r²=0由于直线与圆相切，所以直线只有一个交点，即判别式等于0，即有：Δ=4k²b²-4(1+k²)(b²-r²)=0化简得：(k²+1)r²=b²解得：b=r√(k²+1)由直线方程y=kx+b，可得直线长度为：l=√(1+k²)由此可得切线的长度为：2l=2√(1+k²)即圆的切线长定理成立。

三、圆的切线长定理的推论根据圆的切线长定理，我们可以得出以下推论：推论1：若直线过圆的直径中点，则直线与圆相切。

证明：设直线方程为y=kx+b，过圆的直径中点，则直线过圆心，即切点的坐标满足直线方程和圆的方程，即有：kx₀+b=y₀x₀²+y₀²=r²将直线方程中的y用x和b表示，代入圆的方程，得到：x²+(kx+b)²=r²化简得：(1+k²)x²+2kbx+b²-r²=0由于直线过圆的直径中点，所以切点的坐标满足圆的方程，即有：x₀²+y₀²=r²将x₀²+y₀²=r²代入直线方程，得到：(1+k²)x₀²+2kbx₀+b²-r²=0由于直线方程与圆的方程有唯一交点，所以判别式等于0，即有：Δ=4k²b²-4(1+k²)(b²-r²)=0化简得：(k²+1)r²=b²由于直线方程过圆心，即切线的长度为0，所以有：b=0解得：k=0即斜率为0，即直线垂直于x轴，即直线过圆的直径中点。

切线长定理的内容
切线长定理是一个关于圆的基本定理，它又称为切线定理或割线定理。

该定理表明，如果有一条直线与圆相交，那么这条直线的切线长等于该直线与圆的交点处的切线段长和外切线段长之和。

具体来说，如果一条直线与圆相交于点A和B，且垂直于半径OC，则该直线在点A和B处的切线段长分别表示为AM和BN，外切线段长表示为MB或AN，则切线长定理可以表示为以下等式：
AM + MB = BN + AN
其中，AM和BN是切线段长，MB和AN是外切线段长。

这个定理对几何学和物理学都有广泛的应用，例如在求解光学中透镜的成像问题时，切线长定理可以用来计算光线的折射角度。

需要注意的是，当直线与圆相切时，切线段长等于外切线段长，此时切线长定理变为以下形式：
AM = BN
切线长定理是圆的基本定理之一，它不仅可以用来解决几何学中的问
题，还有许多应用于实际生活和工程领域的实际问题。