比较分数大小的五种方法

对于两个不同的分数，有分母相同，分子相同以及分子、分母都不相同三种情况，其中前两种情况判别大小的方法是：分母相同的两个分数，分子大的那个分数比较大；分子相同的两个分数，分母大的那个分数比较小。

第三种情况，即分子、分母都不同的两个分数，通常是采用通分的方法，使它们的分母相同，化为第一种情况，再比较大小。

由于要比较的分数千差万别，所以通分的方法不一定是最简捷的。

下面我们介绍另外几种方法。

1.“通分子”。

当两个已知分数的分母的最小公倍数比较大，而分子的最小公倍数比较小时，可以把它们化成同分子的分数，再比较大小，这种方法比通分的方法简便。

如果我们把课本里的通分称为“通分母”，那么这里讲的方法可以称为“通分子”。

2.根据倒数比较大小。

3.若两个真分数的分母与分子的差相等、则分母（子）大的分数较大；若两个假分数的分子与分母的差相等，则分母（子）小的分数较大。

分数混合运算式，要注意分数小数之间的互化，已达到简算的目的，同时考虑运算律的应用。

分数比较大小典型例题知识梳理【例1】★比较777773777778 和888884888889的大小。

【解析】这两个分数的分子与分母各不相同，不能直接比较大小，使用通分的方法又太麻烦。

由于这里的两个分数都接近1，所以我们可先用1分别减去以上分数，再比较所得差的大小，然后再判断原来分数的大小。

因为1－777773777778 =5777778 ，1－888884888889 =58888895777778 ＞5888889所以777773777778 ＜888884888889。

【小试牛刀】比较77777757777777 和66666616666663的大小。

【解析】77777757777777 ＞66666616666663【例2】★比较1111111 和111111111哪个分数大？ 【解析】可以先用1分别除以这两个分数，再比较所得商的大小，最后判断原分数的大小。

第五讲分数的大小比较及运算教学目标：1.理解有关概念，能正确地约分和通分，能正确地比较分数的大小。

2.进一步理解和掌握分数加减法、乘法、除法的计算法则，并能正确地运算，力求做到计算方法的灵活、合理。

3.能正确地解答分数运算文字叙述题和应用题，进一步培养学生分析问题和解决简单实际问题的能力。

知识梳理：1.最简分数和约分：２.分数的大小比较：比较约分和通分3.分数的加减：通分定义：将异分母的分数分别化成与原分数大小相等的同分母的分数，这个过程叫通分。

最小公倍数作为公分母异分母分数大小比较：先通分，再比较大小比较方法：同分母时，通分，比较分子； 同分子时，比较分母； 化成小数，再比较；利用数轴比较大小；对角相乘法约分通分 相同点不同点利用分数的基本性质保证分数值不变将一个分数化成数字较小的等值分数将分母不同的几个分数化成与各自原分数等值的分母相同的分数定义： 真分数：分子比分母小的分数叫真分数（真分数小于1）假分数：分子大于或等于分母的分数（假分数大于或等于1）4.分数的乘法：bd ac d c b a =⨯ 两个分数相乘，将分子相乘的积作分子 ，分母相乘的积作分母。

b ma b a m =⨯ 整数×分数：整数与分子相乘，分母不变()acbdmad c d ab mac d ab m +=⨯+=⨯ 带分数先化成假分数，再乘分数相乘，可先约分再乘；结果一定是最简分数一个正数乘以一个大于 1 的数，将会增大，一个正数乘以一个小于 1 的数，将会变小 5.分数的除法：倒数定义：1 除以一个不为零的数得到的商，叫这个数的倒数。

()()0,00a1≠≠≠q p qp pq a a 的倒数是的倒数是互为倒数的两个数的乘积为 1 ；“0”没有倒数分数的除法定义：甲数除以乙数（0除外），等于甲数乘以乙数的倒数。

法则：()0,0,0≠≠≠=⨯=÷q p n mqnp q p m n p q m n除法乘法除以一个数相当于乘以一个数的倒数（求带分数的倒数：先把带分数化成假分数，再求倒数）精讲精练：1.比较下列每组两个分数的大小.同分母的分数相加减：bd a bd ba ±=±异分母的分数相加减：bcbd ac cd ba ±=± 带分数的加减：整数±整数； 真分数±真分数 或化成假分数再运算加减法则：（1）97____98； （2）1311____1411； （3）72____145；（4）85____94； （5）925___ 415； （6）20062005____20052006.（7）433___415. （8）831 4.2.计算： （1）83+127； （2）65-31 （3）32+41-51； （4）43+65-87.（5）125-187； （6）167+203； （7）41-61+81； （8）43+127-65.（9）911972+（10）2126792155753-++ （11）11111211⨯ （12）512512÷（13） 41154⨯ （14）543÷（15）871÷（16）1872÷3.（1）计算：)1011)(911)(811)(711)(611()511()411()311()211(-----⨯-⨯-⨯-⨯-（2）. 已知735的倒数为m ，n 的倒数为732，求m ＋n 的倒数.4．解答题（1） 小红每天在校练琴43小时，5天她在学校练琴多少小时？（2） 如果一集电视剧放映53小时，那么3集电视剧要放映多少小时？（3）一块试验田的53种水果，而种西瓜的田又占了种水果的田的41，问种西瓜的田占总试验田的几分之几？（4）. 一个长方体的长、宽、高分别为65ｃｍ、43ｃｍ、311ｃｍ、求它的表面积.（5）小明去超市购了50元的货物，用去了所带钱款的54，求小明带了多少钱款去超市购物？（6） A 、B 两地相距34千米，甲用了652小时行完全程，如果甲每小时多行51千米，则甲从A 到B 共需多少时间？课堂练习：一、填空题1．用分数表示除法的商:1217÷ =__________.2. 写出下列图中的阴影部分面积各占总面积的几分之几.（ ） （ ） （ ） 3. 一段公路5千米，8天修完，平均每天修_____千米，每天修这段公路的_______. 4. )(920)(43==÷.5. 分数2772、1751、4297中，最简分数是 .6. 用最简分数表示:25分钟是1小时的__________.7. 某班男同学有20人，女同学有25人，该班男同学人数占全班人数的_______. 8. 比较大小:34___1012(填“>”或“<”)9. 若3546x <<,且x 是分母为48的最简分数,则x =_________.10. 加工同样多的零件,王师傅用了1314小时,张师傅用了1213小时,李师傅用了1516小（A 、B 为两边中点）时,____师傅最快. 二、选择题(4×3分=12分)11.下列说法中正确的是( )（A ）分数的分子和分母中一个是奇数,另一个是偶数,这个分数一定是最简分数; （B ）一个分数的分子与分母是两相邻的正整数,这个分数一定是最简分数; （C ）一个分数的分子、分母都是合数时，这个分数一定不是最简分数; （D ）因为13>8,29>9,所以138299.12. 把分数a b的分子扩大3倍，分母缩小2倍，所得的分数比a b（ ）（A ）扩大6倍; （B ）扩大5倍; （C ）缩小6倍; （D ）不变. 13．一段布料，用去5米，还剩3米，用去的是这段布料的（ ） （A ）35; （B ）25; （C ）58; （D ）38.14．下列各数中,大于13且小于12的数是( )（A ）512; （B ）413; （C ）712; （D ）612.三、解答题(8分+6分+9分+3×7分+2×8分=60分)15.在数轴上标出以下各点,并把各点所表示的数按从小到大的顺序排列.A 点表示的数为23,B 点表示的数为4,C 点表示的数为54,D 点表示的数为125.16. 把相等的分数用线连起来.（1）41602597 （2）573811569521256349100255332853417. 先通分，再比较每组中分数的大小. (1)241785和(2)1271811和(3)94、2158和4518. 小萍找来三根丝做手工作业，第一根铁丝的长度是第二根的2倍，第三根铁丝长度是第二根的6倍，第一根铁丝的长度是第三根的几分之几？19. 某工程队7天内修2千米，那么每天修多少千米？每天修工程的几分之几？20. 某班一次数学测验的成绩统计如下表所示,求80～100分的人数占全班人数的几分之几?不及格人数占全班人数的几分之几?21. 超市有一批苹果150千克,一天卖出50千克,还剩这批水果的几分之几?22. 给一个圆面的正反面分别涂上红色和黄色,它们所占整个圆面的大小如下图所示,试说明哪种颜色涂的面积大.23.(附加题) 一个分数的分子，分母相差3，如果分子、分母同时加上13后，可约简成76，求原分数.回家作业： 一、填空题1、把下列带分数化成假分数：532＝ ；2034＝ ；875＝ .2、265分钟＝（ ）小时（填分数）3、如果每根水管长432米，那么8根这样的水管长为 米.4、六年级某班共有45名学生，一次体格检验后，老师宣布全班92的同学体重超标，那么这个班体重超标的学生有 名.红黄黄黄黄黄红5、小明今年15岁，比她爸爸小30岁，5年后小明的年龄是她爸爸年龄的()()？ 6、仓库有货810吨，9天运走全部的53，平均每天运走 吨.7、上海“金贸大厦”的高度约是420米，共有88层，那么它每层的平均高度是 米. 8、“沪宁高速公路”开通前汽车从上海到南京要319小时，开通后只需213小时，这样从上海到南京可以节省 小时. 9、小王身高175厘米，小丁比小王矮51，那么小丁身高 厘米.二、选择题13、某数应该乘于52，却错乘了52的倒数，得数是158，这个数是（ ）(A) 34 (B) 43 (C) 7516 (D)167514、一盘录像带的价格是45元，相当于一盘光碟价格的43，一盘光碟的价格是多少元？下列列式中正确的 是（ ） (A) ;4145⨯(B) );431(45+⨯ (C) ;4345÷(D).4543÷15、下列说法不正确的是（ ） (A)山羊的只数比绵羊的多31，就是绵羊的只数比山羊的少31；(B)把10克的盐溶解到40克的水中，盐的重量占盐水重量的;41(C)甲比乙多83，如果把乙看成单位“1”，甲就相当于乙的“831-”； (D)甲比乙多83，如果把甲看成单位“1”，乙就相当于甲的“831+”；16、班级开“六一儿童节”庆祝会，预计活动费用400元，实际用了360元,下列结论正确的是（ ）(A)实际费用是计划费用的109； (B) 实际费用比计划费用少;101(C)计划费用比实际费用多;101 (D)实际费用比计划费用少40元；。

比较有理数大小的类型与方法一、两个有理数比较大小，可以归纳为五种情况：（1）两个正数，如3和310； 分析：1、一个分数和一个小数比较大小时，要统一成分数或者小数，一般统一成小数；2、异分母的两个分数比较大小时，先通分再比较。

（2）正数和0，如3和0；分析：由“比较大小的法则：正数大于零”，直接可得出3>0（3）负数和0，如-2和0；分析：由“比较大小的法则：负数小于零”，直接可得出-2<0（4）一个负数和一个正数，如-2和3；分析：由“比较大小的法则：负数小于正数”，直接可得出-2<3（5）两个负数，如-2和-3。

分析：因为33,22=-=-，2<3，由“两个负数比较大小，绝对值大的反而小”，可得-2>-3二、比较有理数大小的方法方法一：利用数轴比较有理数的大小数轴上的点表示的数，右边的总比左边的大。

例1：在数轴上表示下列各数，并比较它们的大小：－35，0,1.5，－6,2，－514. 解：如图所示.－6＜－514＜－35＜0＜1.5＜2. 例2：如图，有理数a 在数轴上的位置如图所示，则( )A.a＞2B.a＞－2C.a＜0D.－1＞a解：选B例3：大于-2.5而小于3.5的整数共有个。

解：6个例4：已知a＞0，b＜0，且b＞a，试比较a、a-、b、b-的大小。

解：根据题意画出数轴，如图在数轴上表示a-、b-的点。

根据“数轴上的点表示的数，右边的总比左边的大”，可得b＜-a＜a＜-b方法二：利用比较大小的法则比较有理数大小。

正数大于0，负数小于0，正数大于负数。

两个负数比较大小，绝对值大的反而小。

例5：在3，－9,412，－2四个有理数中，最大的是()A.3B.－9C.412 D.－2解：选C方法三：利用特殊值比较有理数的大小。

例6：比较2a与3a的大小。

解：当0<a时，aa32>当0=a时，aa32=当0>a时，aa32<。

课堂实录：北师大版五年级上册数学《5.9 分数的大小》时间：2023年3月20日上午第二节课地点：五年级二班教室教师：张老师【课堂导入】张老师：同学们，我们今天要学习的是分数的大小比较。

你们知道，分数是表示整体的一部分，那么如何比较两个分数的大小呢？这就是我们今天要探讨的问题。

【新课讲解】张老师：首先，我们来复习一下分数的基本概念。

分数由分子和分母组成，分子表示整体中的部分，分母表示整体被分成了几份。

比如，2/5表示一个整体被分成了5份，取其中的2份。

张老师：那么，如何比较两个分数的大小呢？这里有几种方法。

方法一：通分法。

当两个分数的分母不同时，我们可以通过找到它们的最小公倍数，将它们通分，然后比较分子的大小。

比如，比较3/4和2/5的大小，我们可以将它们通分为15/20和8/20，显然15/20大于8/20，所以3/4大于2/5。

方法二：约分法。

当两个分数可以约分时，我们先约分，然后再比较大小。

比如，比较6/9和4/6的大小，我们可以将它们都约分为2/3，显然2/3等于2/3，所以6/9等于4/6。

方法三：直接比较法。

当两个分数的分母相同时，我们可以直接比较分子的大小。

比如，比较5/7和6/7的大小，显然5/7小于6/7。

【课堂练习】张老师：接下来，我们来做一些练习题，巩固一下分数大小比较的方法。

1. 比较以下分数的大小，说出你的判断方法。

1/2，3/4，2/32. 给出一个分数，你的同桌给出另一个分数，互相比较大小，看看你们的方法是否一致。

【学生回答】学生1：我选择通分法，将1/2通分为3/6，将3/4通分为4/8，将2/3通分为4/6，然后比较大小。

显然，3/6小于4/6，4/8大于4/6，所以1/2小于3/4小于2/3。

学生2：我选择直接比较法，因为我们的分数分母相同。

我给出的分数是5/8，同桌给出的分数是6/8，显然5/8小于6/8。

【课堂小结】张老师：通过今天的学习，我们掌握了分数大小比较的三个方法：通分法、约分法和直接比较法。

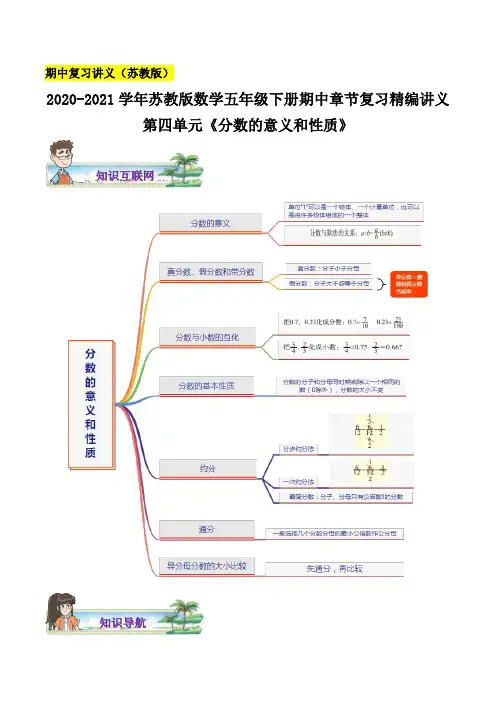
期中复习讲义（苏教版）2020-2021学年苏教版数学五年级下册期中章节复习精编讲义第四单元《分数的意义和性质》知识互联网知识导航知识点一：分数的意义1.一个物体、一个计量单位或由许多物体组成的一个整体，都可以用自然数 1 来表示，通常我们把它叫做单位“1”。

把单位“1”平均分成若干份，表示这样的一份或几份的数叫做分数。

表示其中一份的数，叫做分数单位。

一个分数的分母是几，它的分数单位就是几分之一。

2.分母越大,分数单位越小，最大的分数单位是 1/2。

3.举例说明一个分数的意义：3/7 表示把单位“1”平均分成 7 份，表示这样的 3 份；还表示把 3 平均分成 7 份，表示这样的 1 份。

3/7 吨表示把 1 吨平均分成 7 份，表示这样的 3 份；还表示把 3 吨平均分成 7 份，表示这样的 1 份。

知识点二：分数与除法的关系：1.被除数相当于分数的分子，除数相当于分数的分母。

被除数÷除数= 被除数/除数如果用a 表示被除数，b 表示除数，可以写成a÷b=a/b(b≠0)2.4 米的 1/5 和 1 米的 4/5 同样长。

3.求一个数是(占)另一个数的几分之几，用除法列算式计算。

方法：是（占）前面的数除以后面的数写成分数。

男生人数是女生人数的 3/4，则女生人数是男生人数的 4/3。

知识点三：真分数、假分数和带分数1.分子比分母小的分数叫做真分数；分子比分母大或者分子和分母相等的分数叫做假分数。

2.真分数小于 1。

假分数大于或等于 1。

真分数总是小于假分数。

3.能化成整数的假分数，它们的分子都是分母的倍数。

反过来，分子是分母倍数的假分数，都能化成整数。

(用分子除以分母)4.分子不是分母倍数的假分数，可以写成整数和真分数合成的数，通常叫做带分数。

带分数是假分数的另一种形式。

例如，4/3 就可以看作是 3/3(就是 1)和 1/3 合成的数，写作 1⅓，读作一又三分之一。

带分数都大于真分数，同时也都大于 1。

五年级数学分数大小的比较练习题
1．我来判对错。

（1）通分就是把两个分母不相同的分数化成分母相同的分数。

（ ）
（2）两个分数通分后，都比原来变大了。

（ ）
（3）分子大的分数比较大，分子小的分数比较小。

（ ）
（4）分子相同，分母大的分数比较小，分母小的分数比较大。

（ ）
（5）通分的根据是分数的基本性质。

（ ）
2．把下面每组异分母分数化成同分母分数。

53和75 41和95 98和107 32和179 54和11
5 3．先用分数表示每组中两个算式的商，再比较它们的大小。

（1）2÷3和4÷5
（2）8÷9和5÷8 4．解答题。

（1）雪江冷饮店有三种数量相同的冷饮，星期五的销售情况如下：雪糕售出75，甜筒售出21，冰淇淋售出92。

①根据售出数量的多少按照一定的顺序排列，并用符号表示出来。

②如果这冷饮店要进货，应该多进哪种冷饮？为什么？
（2）做同一种零件，王师傅2小时做15个，李师傅3小时做20个，谁做得快一些？
（3）你能写出一个比71小、比81大的分数吗？
5．小军看一本故事书，第一天看完全书的72，第二天看完全书的154，第三天看完全书的32
9，问三天哪天看得多？ 6．你能写出一个比61
大，又比51小的分数吗？你是怎样找到这个分数
的？你能找到两个这样的分数吗？。

小学奥数知识：分数大小比较的几种方法对于分母或分子相同的分数，可根据同分母或同分子分数比较大小的方法进行比较；对于分母和分子都不相同的分数，通常是采用先通分再比较大小的方法。

实际上，比较分数大小的方法有很多，同学们可根据要比较的分数的特点，选择适当的方法进行比较。

下面就向同学们介绍几种比较分数大小的方法。

一、化同分子法先把分子不同的两个分数化成分子相同的两个分数，然后再根据“分子相同的两个分数，分母小的分数比较大”进行比较。

例1. 比较和的大小。

分析与解：把原来两个分数的分子3和5的最小公倍数15作为两个新分数的分子，根据分数的基本性质可得：，，因为，所以。

二、化成小数法先把两个分数化成小数，再进行比较。

例2. 比较和的大小。

分析与解：先根据分数与除法的关系，把这两个分数化成小数，即，……，因为……，所以。

三、搭桥法在要比较的两个分数之间，找一个中间分数，根据这两个分数和中间分数的大小关系，比较这两个分数的大小。

例3. 比较和的大小。

分析与解：根据两个分数的分子和分母的大小关系，把作为中间分数。

可以很容易看出：，，所以。

四、差等规律法根据“分子与分母的差相等的两个真分数，分子加分母得到的和较大的分数比较大；分子与分母的差相等的两个假分数，分子加分母得到的和较大的分数比较小”比较两个分数的大小。

例4. 比较和的大小。

分析与解：这两个真分数的分子与分母的差都是1，因为，所以。

五、交叉相乘法把第一个分数的分子与第二个分数的分母相乘的积当作第一个分数的相对值；把第二个分数的分子与第一个分数的分母相乘的积当作第二个分数的相对值，相对值比较大的分数比较大。

例5. 比较和的大小。

分析与解：因为的相对值为，的相对值为，63>60，所以。

六、比较倒数法通过比较两个分数倒数的大小，比较两个分数的大小。

倒数较小的分数，原分数较大；倒数较大的分数，原分数较小。

例6. 比较和的大小。

分析与解：的倒数是，的倒数是因为，所以。

《分数的大小比较》教学设计顺河小学李绍奎学习目标：1、探索分数大小比较的方法，会正确比较两个分子、分母都不同的分数的大小。

结合具体的情境，引导学生用分数描述有关现象。

2、结合具体情境，理解通分的含义，探索并掌握通分的方法。

3、培养学生善于运用旧知识解决新问题的能力。

学习重点：会用通分的方法比较两个分子、分母都不同的分数的大小。

学习难点：理解通分的含义。

学习过程：一、课前预习1、师：同学们会比较分数的大小吗？（会）一起来看一看，出示：（1）3/4 和 1/4师：你是怎样比较的？生1：分母相同的两个分数，分子大的分数大，分子小的分数小。

师：还有不同的方法吗？生2：可以用画图的方法比较。

师：怎样画图比较？你能在黑板上画出来吗？生在黑板上画图后，集体评价。

师指出，这是单位“1”相同的、两个同分母分数大小比较的方法。

（2）出示：1/2和1/3师：谁能说说这道题与上一道的区别？生：分子相同，分母不同。

师：如何比较大小？生：分子相同，分母大的分数小。

1/2＞1/3.师：能用画图的方法比较吗？谁想在黑板上试着画一画？生画图后，集体评价。

师指出，这是单位“1”相同的、两个同分子的分数比大小的方法。

师：通过回顾旧知识，我们整理出了三种比较分数大小的方法，即画图法、同分母比较法和同分子比较法。

可是，有时候我们会遇到这样的两个分数，它们的分母和分子都不同，你有办法比较它们的大小吗？生沉思中有人小声说“通分”，师借机提问，“通分”是一种方法，你能说一说到底什么是“通分”吗？（生沉默。

）师：这节课我们就会学到如何用“通分”的方法比较两个分母、分子都不同的分数的大小。

揭示课题：分数的大小。

二、激发需要，感受策略1、出示主题图及问题。

（教学楼占校园面积的2/9，操场占校园面积的1/4，操场和教学楼谁的占地面积大？）生默读题目。

师：谁能说一说题目里的2/9和1/4是什么意思？生：2/9表示把校园面积看做单位1，平均分成9份，教学楼占了2份。