7 最大公因数与最小公倍数.doc
- 格式:doc
- 大小:613.50 KB
- 文档页数:12

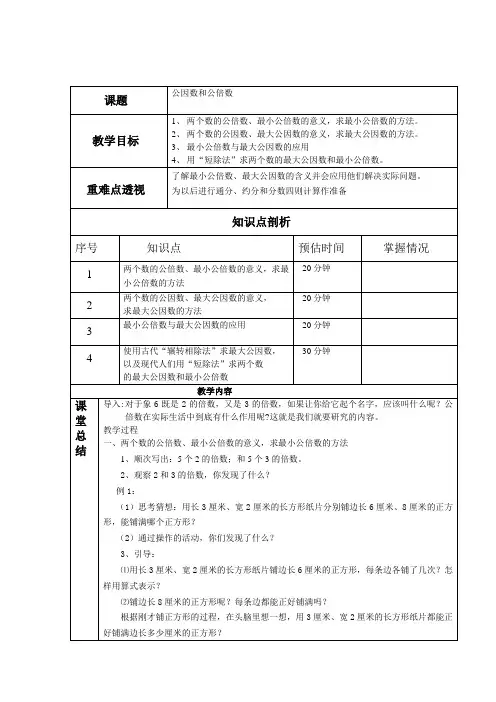
第五讲最大公因数与最小公倍数学法探讨大家知道我们在研究因数和倍数时,0是一个特殊的数;O不是任何自然数的因数(除数不能为O),但0是任何非0自然数的倍数(任何非0自然数的O倍等于0)在本讲中我们只讨论正整数。
几个数公有的因数叫做这几个数的公因数,其中最大的一个,叫做这几个数的最大公因数。
为了书写简便,a、b两数的最大公因数记为(a,b)。
几个数公有的倍数叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,为了书写简便,a、b两数的最小公倍数记为[a,b]。
最大公因数与最小公倍数有以下重要性质:1.两个数的公因数都是它们的最大公因数的因数;2.两个数的公倍数都是它们的最小公倍数的倍数;3.两个数的积,等于它们的最大公因数与最小公倍数的积;即a×b=(a,b)×[a,b]4.两个自然数分别除以它们的最大公因数,所得的商为互质数。
关于“最大公因数和最小公倍数”你还有什么需要补充?请你写在下面:例题选讲【例题1】育才小学拿出一块长方体木料,长180厘米,宽144厘米,高108厘米,请王师傅把它锯成棱长是整厘米数,大小相同的正方体木块,木块的体积要最大,木料又不能剩余,算一算,可以锯成多少块?【分析】要把长方体木料锯成棱长是整厘米数,大小相同的正方体木块,则正方体的棱长应是长方体的长、宽、高的公因数,又要求每小块正方体的体积最大,因此锯成的正方体的棱长必须是长方体的长、宽、高的最大公因数,由此便可得出问题的解答。
【解答】【练习5-1】把一张长60厘米、宽48厘米的长方形纸,裁成若干面积相等边长为整厘米数的小正方形而没有剩余,小正方形的面积最大是多少?【例题2】有一个班的同学去划船,他们算了一下,如果增加一条船,正好每船坐6人,如果减少一条船,正好每船坐9人,这个班有多少人?(第二届全国“华罗庚金杯”少年数学邀请赛初赛试题) 【分析】根据题意,这个班的人数应是6的倍数,又是9的倍数,从而是6和9的公倍数,故只要在6和9的公倍数中寻找符合条件的解,便能得到问题的解答。

最大公因数和最小公倍数定义最大公因数和最小公倍数是数学中两个重要的概念。
它们可以帮助我们解决许多实际问题,例如求解分数的最简形式、解决整数倍数关系等等。
本文将从定义、性质和求解方法等方面介绍最大公因数和最小公倍数的相关知识。
最大公因数定义两个或多个整数的最大公因数,简称最大公因数,是能够整除每一个给定整数的最大正整数。
最大公因数一般用符号“gcd”表示,例如gcd(a,b)表示整数a和b的最大公因数。
性质最大公因数有以下几个重要性质:1.gcd(a,b) = gcd(b,a):最大公因数具有交换律。
2.gcd(a,b) = gcd(a-b,b):欧几里得算法,也称为辗转相除法,利用这一性质求解最大公因数。
3.若c是a和b的公因数,且c是a和b的最大公因数,则c是a和b的最大公因数的倍数。
求解方法求解最大公因数有多种方法,这里介绍两种常用的方法:欧几里得算法和素因数分解法。
欧几里得算法欧几里得算法是一种通过不断求出两个数的余数来迭代计算最大公因数的方法。
算法的步骤如下:1.用较大的数除以较小的数,得到商和余数。
2.用较小的数除以余数,再次得到商和余数。
3.重复上述过程,直到余数为0为止。
4.最大公因数就是最后一次运算中的被除数。
例如,求解gcd(12, 8):12 ÷ 8 = 1 余 48 ÷ 4 = 2 余 0最大公因数为4。
素因数分解法素因数分解法是通过将两个数分别分解成素数因子的乘积,并取两个数相同部分的乘积作为最大公因数。
算法的步骤如下:1.将两个数分别进行素因数分解,得到各自的素因子乘积。
2.取两个数相同部分的乘积作为最大公因数。
例如,求解gcd(12, 8):12 = 2² × 38 = 2³相同部分为2²,最大公因数为4。
最小公倍数定义两个或多个整数的最小公倍数,简称最小公倍数,是能够同时整除每一个给定整数的最小正整数。
最小公倍数一般用符号“lcm”表示,例如lcm(a,b)表示整数a和b的最小公倍数。

最小公倍数和最大公因数的关系证明下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!最小公倍数和最大公因数是初中数学学习中经常遇到的概念,它们之间的关系是数学中一个基础而重要的命题。

第七单元最大公因数与最小公倍数(一)例1:求45、105的最大公因数和最小公倍数。
练习1、求下面几组数的最大公因数和最小公倍数:120和45,25和125,17和91,39和26。
算一算每组两个数的乘积和最大公因数与最小公倍数的乘积。
例2:已知a=30,b=440,c=550,求(a,b,c)和[a,b,c]分别是多少?练习2、求下面几组数的最大公因数和最小公倍数。
4、5和6; 8,12和36; 8,9和10练习3、一盒铅笔,可以平均分给2、3、4、5、6个小朋友,这盒铅笔最少有多少支?练习4、甲数是36,甲、乙两数的最小公倍数是288,最大公因数是4,乙数应该是多少?例3:将一块长357厘米、宽105厘米、高84厘米的长方体木料,锯成同样大小的正方体小木块,当正方体的棱长最大是多少时,大长方体木料无剩余?这时共截出了几个小正方体?例4:长100厘米的木棍,从一端开始每3cm染一个红点,每5cm染一个蓝点。
然后将染有点的地方锯开,木棍共锯成多少段?练习5.一张长方形的纸,长为96厘米,宽为60厘米,把它裁成同样大小且边长为整厘米数的正方形而无剩余,问至少可以裁多少张?练习6、三根铁丝,长度分别是120厘米、180厘米、300厘米,现在要把它们截成相等的小段,每段都不能有剩余,那么每小段长多少厘米?一共可截成多少段?例5:两个自然数的最大公因数是12,最小公倍数是120,求这两个数练习7、两个小于150的数的积是2028,它们的最大公因数是13,求这两个数。
练习8.已知a与b,a与c的最大公因数分别是12和15,a,b,c的最小公倍数是120,求a,b,c?练习9、如果甲乙两数的最大公因数是6,最小公倍数是90,如果甲数是18,那么乙数是多少?练习10.加工某种零件,需要三道工序,第一道工序的工人,每人每小时可完成48个,第二道工序的工人,每人每小时可以完成32个,第三道工序的工人,每人每小时可以完成28个,问三道工序至少各要多少工人时,搭配才算最合适?练习11、大雪后的一天,亮亮和爸爸从同一点出发沿同一方向分别步测一个圆形花圃的周长。


几个数共有的倍数叫做这几个数的公倍数,其中除0以外最小的一个公倍数,叫做这几个数的最小公倍数。
自然数a、b的最小公倍数可以记作[a,b],自然数a、b的最大公因数可以记作(a、b),当(a、b)=1时,[a、b]= a×b。
如果两个数是倍数关系,则它们的最小公倍数就是较大的数,相邻的两个自然数的最小公倍数是它们的乘积。
最小公倍数=两数的乘积/最大公约(因)数, 解题时要避免和最大公约(因)数问题混淆。
[1]最小公倍数的适用范围:分数的加减法,中国剩余定理(正确的题在最小公倍数内有解,有唯一的解).因为,素数是不能被1和自身数以外的其它数整除的数;素数X的N次方,是只能被X的N-1以下次方,1和自身数整除.所以,在求A,B,C,D,E,…,Z的最小公倍数时,只需要把这些数分解为素数的N次方之间的乘积后,取各素因子的最高次方的乘积,就是这些数的最小公倍数.举例说明:求756,4400,19845,9000的最小公倍数?因756=2*2*3*3*3*7,4400=2*2*2*2*5*5*11,19845=3*3*3*3*5*7*7,9000=2*2*2*3*3*5*5*5,这里有素数2,3,5,7,11.2最高为4次方16,3最高为4次方81,5最高为3次方125,7最高为2次方49,还有素数11.得最小公倍数为16*81*125*49*11=87318000.例题1两个数的最大公因数是15,最小公倍数是90,求这两个数分别是多少?15×1=15,15×6=90;当a1b1分别是2和3时,a、b分别为15×2=30,15×3=45。
所以,这两个数是15和90或者30和45。
练习一1,两个数的最大公因数是9,最小公倍数是90,求这两个数分别是多少?2,两个数的最大公因数是12,最小公倍数是60,求这两个数的和是多少?3,两个数的最大公因数是60,最小公倍数是720,其中一个数是180,另一个数是多少?例题2两个自然数的积是360,最小公倍数是120,这两个数各是多少?上!!分析我们把这两个自然数称为甲数和乙数。

最大公因数与最小公倍数(一)一、互质数的意义和判断方法1.明确互质数的意义公因数只有1的两个数叫做互质数。
2.明确互质数的判断方法互质数有很多种情况,不是只有两个质数才是互质数,合数和合数也可能成为互质数。
判断两个数是不是互质数,就看它们是不是只有唯一的公因数1。
练习1:分别写出5组满足下列条件的互质数:1)两个数都是质数:()、()、()、()、()2)一个质数一个合数:()、()、()、()、()3)两个都是合数:()、()、()、()、()4)两个都是奇数:()、()、()、()、()5)一个奇数一个偶数:()、()、()、()、()3.两个数互质的特殊的判断方法1) 1和任意大于1的自然数互质;2) 2和任何奇数都是互质数;3) 相邻的两个自然数是互质数;4) 相邻的两个奇数是互质数;5) 不相同的两个质数是互质数;6) 一个合数与一个质数是互质数(合数只质数的倍数除外)4.互质数和质数的区别质数一类数,是只有两个因数的数;互质数是相对于两个数的关系而言,公因数只有1的两个数才可称为互质数。
练习2:判断:1) 互质的两个数没有最大公因数。
.....................................()2) 两个数的公因数的个数是有限的。
..................................()3) 1和任意非零自然数的最大公因数是1。
............................()4)最小的质数和最大的合数的最大公因数是1。
....................()填空:1) 在7,15,9,20四个数中,成为互质数的有()对二、最大公因数与最小公倍数1.基础巩固例1 填空。
1)53⨯⨯b,a,b的最大公因数是(),最小公倍数是()。
=3a,532⨯⨯=2)a与b是互质数,a,b的最大公因数是(),最小公倍数是()。
3)b=(a,b都是大于0的自然数),a,b的最大公因数是(),最小公倍数是()。

最大公因数和最小公倍数最大公因数和最小公倍数是数学中常见的概念,在学习数论和代数的过程中经常会遇到。
本文将详细介绍最大公因数和最小公倍数的定义、性质、计算方法以及相关的应用。
第一篇:最大公因数最大公因数(Greatest Common Divisor,简称GCD)是指两个或多个整数中能够同时整除它们的最大正整数。
对于两个整数a和b,它们的最大公因数通常用符号gcd(a, b)表示。
最大公因数有以下性质:1. gcd(a, 0) = a,即任何非零整数和0的最大公因数都等于其本身。
2. gcd(a, b) = gcd(b, a),即最大公因数的计算与顺序无关。
3. gcd(k·a, k·b) = k·gcd(a, b),即最大公因数与常数因子的关系。
计算最大公因数的方法有多种,以下是常见的两种方法:1. 辗转相除法:又称欧几里德算法,基于以下定理:若a能整除b,且r为a除以b的余数,那么gcd(a, b) =gcd(b, r)。
通过重复应用这个定理,不断用余数替换原先的除数,直到余数为0,此时的除数即为最大公因数。
2. 素因数分解法:将两个数分解为质因数的乘积,然后找出相同的质因数,并将它们相乘。
得到的结果即为最大公因数。
最大公因数在数学中有广泛的应用,例如简化分数、求解线性方程和求解同余方程等。
它在计算机科学和密码学中也有重要的应用,如最大公因数算法在RSA加密中的应用。
第二篇:最小公倍数最小公倍数(Least Common Multiple,简称LCM)是指两个或多个整数中能够同时被它们整除的最小正整数。
对于两个整数a和b,它们的最小公倍数通常用符号lcm(a, b)表示。
最小公倍数有以下性质:1. lcm(a, 0) = 0,即任何非零整数和0的最小公倍数都为0。
2. lcm(a, b) = lcm(b, a),即最小公倍数的计算与顺序无关。
3. lcm(k·a, k·b) = k·lcm(a, b),即最小公倍数与常数因子的关系。


公因数、最大公因数、公倍数和最小公倍数公因数、最大公因数、公倍数和最小公倍数在数学中,我们常常需要求出多个数的公因数、最大公因数、公倍数和最小公倍数。
掌握这些概念和求法是非常重要的。
最大公因数是几个数公有的因数中最大的那个,可以用列举法、观察法和短除法等方法求得。
例如,求8和6的最大公因数,我们可以先列出它们的因数,然后找出它们的公因数,最后找出它们的最大公因数,即2.观察法可以应用于特殊情况,例如两个数具有倍数关系时,它们的最大公因数就是其中较小的数;两个数是互质数时,它们的最大公因数就是1.如果两个数不是倍数和互质关系,我们可以用小数缩小法,即把较小的数缩小,每次缩小后看得到的商是不是另一个数的因数,直到所得的商是另一个数的因数为止。
短除法是一般情况下求最大公因数的常用方法。
我们可以用这两个数除以它们的公因数,一直除到所得的两个商只有公因数1为止。
然后把最后所有的除数连乘,就得到了二个数最大公因数。
除了最大公因数,我们还需要掌握最小公倍数的求法。
最小公倍数是几个数公有的倍数中最小的那个,可以用列举法、分解质因数法和公式法等方法求得。
例如,求6和8的最小公倍数,我们可以先列出它们的倍数,然后找出它们的公倍数,最后找出它们的最小公倍数,即24.最后,我们需要学会如何解有关最大公因数和最小公倍数的应用题,例如求某些数的最大公因数或最小公倍数,或者求某些数的倍数关系等。
通过练,我们可以更好地掌握这些知识点,并在实际问题中灵活运用。
12和24的最大公因数是4,可以表示为(12,24)=4.互质数是指公因数只有1的两个数,例如1和任何自然数都是互质数,相邻两个自然数如2和3、8和9也是互质数。
两个质数一定是互质数,而两个合数可能是互质数,例如8和9、25和49.2和所有奇数都是互质数,质数与比它小的合数也是互质数。
需要注意的是,质数是对一个数来说,而互质数是对两个数的关系来说的。
在练中,需要判断每组数是不是互质关系或倍数关系,并求出它们的最大公因数。
公因数、最大公因数、公倍数和最小公倍数1、掌握最大公因数和最小公倍数的求法;2、会解有关最大公因数和最小公倍数的应用题;【知识点1】最大公因数几个数公有的因数叫这些数的公因数。
其中最大的那个就叫它们的最大公因数。
【知识点2】最大公因数求法1、列举法先找出两个数的(因数),再找出两个数的(公因数),最后找出二个数的(最大公因数)找8和6的最大公因数8的因数有1、2、4、86的因数有1、2、3、68和6的最大因数数是2。
2、观察法(特殊情况)1)两个数具有倍数关系的,它们的最大公因数就是其中较小的数。
2)两个数是互质数的(互质数就是两个数只有公因数1),它们的最大公因数就是1。
3)两个数不是倍数和互质关系,用小数缩小法案件分解:两个数具有倍数关系的,它们的最大公因数是其中较小的数。
8和16的最大公因数( 8 ) 4和8的最大公因数( 4 )9和3的最大公因数( 3 ) 28和7的最大公因数( 7 )两个数是互质数的(互质数就是两个数只有公因数1),它们的最大公因数就是1。
相邻两个自然数(0除外)2和3的最大公因数是( 1 ) 8和9的最大公因数是( 1 ) 99和98的最大公因数是( 1 )两个不同的质数5和7的最大公因数是( 1 ) 17和29的最大公因数是( 1 ) 11和19的最大公因数是( 1 )两个互质的合数4和9的最大公因数是( 1 ) 20和49的最大公因数( 1 ) 25和69的最大公因数是( 1 )两个数不是倍数和互质关系,用小数缩小法把较小的数缩小(除以2、3、4……)每次缩小后看得到的商是不是另一个数的因数,直到所得的商是另一个数的因数为止。
18和48的最大公因数先用小数 18÷2=9,9不是48的因数,18÷3=6,6是48的因数,那么18和48的最大公因数6。
16和36的最大公因数16÷2=8,8不是36的因数,16÷4=4,4是36的因数,那么16和36的最大公因数4。
第三讲最大公因数和最小公倍数一.基本概念和知识1.公因数和最大公因数几个数公有的因数,叫做这几个数的公因数;其中最大的一个,叫做这几个数的最大公因数。
2.公倍数和最小公倍数几个数公有的倍数,叫做这几个数的公倍数;其中最小的一个,叫做这几个数的最小公倍数。
3.互质数如果两个数的最大公因数是1,那么这两个数叫做互质数。
二.例题例1:用一个数去除30、60、75,都能整除,这个数最大是多少?分析∵要求的数去除30、60、75都能整除,∴要求的数是30、60、75的公因数。
又∵要求符合条件的最大的数,∴就是求30、60、75的最大公因数。
解:(30,60,75)=15所以,这个数最大是15。
例2:一个数用3、4、5除都能整除,这个数最小是多少?分析由题意可知,要求求的数是3、4、5的公倍数,且是最小公倍数。
解:∵ [3,4,5] =60,∴用3、4、5除都能整除的最小的数是60。
例3:有三根铁丝,长度分别是120厘米、180厘米和300厘米。
现在要把它们截成相等的小段,每根都不能有剩余,每小段最长多少厘米?一共可以截成多少段?分析∵要截成相等的小段,且无剩余,∴每段长度必是120、180、300的公因数;又∵每段要尽可能长,∴要求的每段长度就是120、180、300的最大公因数。
解:∵(120,180,300)=60,∴每小段最长60厘米。
120÷60+180÷60+300÷60=2+3+5=10(段)答:每段最长60厘米,一共可以截成10段。
例4:加工某种机器零件,要经过三道工序。
第一道工序每个工人每小时可完成3个零件,第二道工序每个工人每小时可完成10个,第三道工序每个工人每小时可完成5个。
要使加工生产均衡,三道工序至少各分配几个工人?分析要使加工生产均衡,各道工序生产的零件总数应是3、10和5的公倍数。
要求三道工序“至少”要多少工人,要先求3、10和5的最小公倍数。
解:∵[3,10,5]=30∴各道工序均应加工30个零件。
求最大公因数和最小公倍数的方法
一、求最大公因数的方法。
1. 辗转相除法。
辗转相除法,又称欧几里得算法,是求最大公因数的一种常用方法。
具体步骤如下:
(1)用较大数除以较小数,得到余数;
(2)用较小数除以余数,再得到新的余数;
(3)继续用新的余数去除上一步的余数,直到余数为0;
(4)此时,除数就是最大公因数。
2. 素因数分解法。
素因数分解法是将两个数分别进行素因数分解,然后将它们共有的素因数相乘,即可得到最大公因数。
二、求最小公倍数的方法。
1. 素因数分解法。
求最小公倍数的一种常用方法是素因数分解法。
具体步骤如下:(1)将两个数分别进行素因数分解;
(2)将它们的素因数分别列出来;
(3)将它们共有的素因数和非共有的素因数分别相乘,即可得
到最小公倍数。
2. 最大公因数和最小公倍数的关系。
最大公因数和最小公倍数之间有着重要的数学关系,即两个数
的最大公因数与最小公倍数的乘积等于这两个数的乘积。
这一性质
在实际问题中有着重要的应用,可以帮助我们更好地理解和运用最
大公因数和最小公倍数。
三、总结。
通过本文的介绍,我们了解了求最大公因数和最小公倍数的几种常用方法,包括辗转相除法、素因数分解法等。
这些方法在实际问题中有着重要的应用,可以帮助我们更好地理解和运用最大公因数和最小公倍数。
希望本文能够对大家有所帮助,更好地掌握这一数学概念。
第一章最大公因數與最小公倍數1-1 因數與倍數一、因數與倍數※學習單一◎定義:1、對於兩個不為0的整數A、B,如果A可以被B 整除﹙餘數為0﹚A ÷ B = C 0我們就可以說A是B的倍數,B是A的因數2、對於A、B、C三個不為0的整數,如果A =B × CA是B、C的倍數,B、C都是A的因數被除數÷除數= 商數,被除數= 除數×商數EX:12 ÷ 3 = 4… 0 12 = 3 × 412是3的倍數,3是12的因數12是3、4的倍數,3、4是12的因數例:1、判別18是否為432的因數2、下列何者是3的倍數﹖﹙1﹚1234﹙2﹚2468﹙3﹚4680﹙4﹚57803、曉華把36個蘋果分成數堆﹙包含分成一堆﹚,每堆的個數相同,總共有幾種分法﹖請一一寫出4、下列何者是2的倍數也是3的倍數﹖﹙1﹚166﹙2﹚216﹙3﹚386﹙4﹚496◎性質:1、一個大於1的整數,至少有1和他自己本身兩個因數2、1是最小的正因數3、1的特性:1是任何整數的因數﹙1能整除任何數﹚,而任何整數都是1的倍數4、0的特性:﹙除數不能為0﹚0不是任何整數的因數,而0是任何不是0的整數的倍數例:1、396是下列哪些數的倍數﹖1、4、11、19、36、3962、273被一整數整除,所得的商數不可能是下面哪一個數﹖﹙1﹚273﹙2﹚21﹙3﹚26﹙4﹚13、下列敘述那一個是正確的﹖﹙1﹚0是2的因數﹙2﹚5是1的因數﹙3﹚1是3的因數﹙4﹚0是0的倍數二、2、3、4、5、8、9、11的倍數的判別法※學習單二◎定義:﹙一﹚、2的倍數判別法:如果一個整數的個位數字是偶數﹙0、2、4、6、8﹚例:1、判別下列何者為2的倍數﹖12、37、124、311、2724、94682、如果四位數237□是2的倍數,那麼□內可以填入哪些數字呢﹖3、如果四位數2□70是2的倍數,那麼□內可以填入哪些數字呢﹖﹙二﹚、5的倍數判別法:如果一個整數的個位數字是0或5例:1、判別下列何者為5的倍數﹖2340、218763、5559、99999952、1234、1235、……、1248等數中,哪些是5的倍數﹖﹙三﹚、3的倍數判別法:如果一個整數的各位數字總和是3的倍數例:1、判別下列何者為3的倍數﹖12、37、124、311、2724、94682、1000011與3721這兩個數,哪一個是3的倍數﹖3、如果四位數27□4是3的倍數,那麼□內可以填入哪些數字呢﹖﹙四﹚、9的倍數判別法:如果一個整數的各位數字總和是9的倍數例:1、判別下列何者為9的倍數﹖12、37、126、378、2724、94682、27369與100012這兩個數,哪一個是9的倍數﹖3、如果五位數73□84是9的倍數,那麼□內可以填入哪些數字呢﹖※補充﹙五﹚、4的倍數判別法:一個整數末兩位數字是4的倍數或均為0 例:1、判別下列何者為4的倍數﹖12、37、124、311、2724、94682、如果四位數27□4是4的倍數,那麼□內可以填入哪些數字呢﹖﹙六﹚、8的倍數判別法:一個整數末三位數字是8的倍數或均為0 例:1、判別下列何者為8的倍數﹖2724、3824、5311、5408、94682、如果四位數2□64是8的倍數,那麼□內可以填入哪些數字呢﹖﹙七﹚、11的倍數判別法:一整數的奇位數字和與偶位數字和的差為0或11的倍數例:1、判別下列何者為11的倍數﹖1547、217481、314822、如果六位數86□170是11的倍數,那麼□內可以填入哪些數字呢﹖三、練習1、下列哪些是3的倍數﹖5的倍數﹖11的倍數﹖3456、3465、285714、20303042、下列敘述是否正確﹖請在適當的□中打「ˇ」正確不正確﹙1﹚5是15的因數□□﹙2﹚6是12的倍數□□﹙3﹚1是10的因數□□﹙4﹚2是13的倍數□□3、有一個七位數432□905,﹙1﹚如果他是3的倍數,那麼□裡可以是多少﹖﹙2﹚如果他是11的倍數,那麼□裡可以是多少﹖4、填填看,在每個□內填入一個適當的數字,15□ = 2 ×□□請將所有可能的情形都列出來。
一、知识总结1、公因数和最大公因数的意义:几个数公有的因数叫做这几个数的公因数,其中最大的一个叫做它们的最大公因数。
2、公因数的特征:一个数的因数的个数是有限的,因此两个数的公因数的个数也是有限的,最小的公因数是1。
3、公倍数和最小公倍数的意义:几个数公有的倍数叫做这几个数的公倍数,其中最小的一个叫做它们的最小公倍数。
4、公倍数的特征:一个数的倍数的个数是无限的,因此两个数的公倍数的个数也是无限的,只有最小公倍数,没有最大公倍数。
5、求两个数的最大公因数与最小公倍数的特殊情况:(1)当两个数成倍数关系时,较小数就是这两个数的最大公因数;较大数就是这两个数的最小公倍数。
(2)如果两个数只有公因数1,那么这两个数的最大的公因数是1;最小公倍数是它们的乘积。
(3)如果两个数都是质数或者两个数是连续的自然数,那么这两个数的乘积就是它们的最小公倍数。
6、分子比分母小的分数叫真分数;真分数小于1。
分子比分母大的分数叫假分数;假分数大于1。
像112,314,…这样的分数叫带分数。
二、练习1.填空题:(1) 37表示把( )平均分成( )份,取其中的( )份。
(2)把一根3米长的绳子平均截成8段,每段是这根绳子的( )( ) ,每段( )( )米。
(3) 34 里面有3个( ),2里面有( )个15 ,10个113是( ),( )个115 是1315。
(4)237的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数就是3。
(5)甲数是4,乙数是15,甲数是乙数的( )( ) ,乙数是甲数的( )( ) 。
(6)分数单位是18的最大真分数是( ),最小的假分数是( )。
(7)717是一个( )分数,它的分数单位是( ) ,它有( )个这样的分数单位,把它化成带分数是( )。
(8)72的分子增加4 ,要使分数的大小不变,分母应增加( )。
(9)在括号里填上合适的分数。
800 千克=( )吨 25 厘米=( )米1400 米=( )千米 45 分=( )小时7 平方米50 平方分米 =( )平方米2.判断题:(1)把单位“1”分成6份,其中的5份,就是56。
7和8的最大公因数和最小公倍数。
7和8的最大公因数和最小公倍数是什么?最大公因数,又称最大公约数,是指两个或多个整数共有的约束因数中最大的一个数;最小公倍数是指两个或多个整数共有的倍数中最小的一个数。
首先来计算7和8的最大公因数。
我们可以列举出7和8的约束因数,分别为1、7和1、2、4、8。
其中,1是两个数的公因数,但不是最大的公因数。
最大的公因数是7,因为它是两个数中最大的一个公因数。
所以,7和8的最大公因数是7。
接下来,我们来计算7和8的最小公倍数。
我们可以列举出7和8的倍数,分别为7、14、21、28和8、16、24、32。
其中,28是两个数的公倍数,但不是最小的公倍数。
最小的公倍数是56,因为它是两个数中最小的一个公倍数。
所以,7和8的最小公倍数是56。
通过以上计算,我们得出结论:7和8的最大公因数是7,最小公倍数是56。
最大公因数和最小公倍数在数学中有着广泛的应用。
在分数运算中,我们常常需要求最大公因数来进行分数的约分,以便得到最简形式的结果。
在求解方程或解决实际问题时,最小公倍数也经常被用到。
除了计算最大公因数和最小公倍数,我们还可以使用其他方法来求解。
其中一个常用的方法是质因数分解法。
我们可以将7和8分别进行质因数分解,然后找出它们共有的质因数和独有的质因数,最大公因数就是共有的质因数的乘积,最小公倍数就是两个数的所有质因数的乘积。
对于7,它是一个质数,没有其他的约束因数,所以它的质因数分解就是它本身,即7=7。
对于8,它可以分解为2的3次方,即8=2×2×2。
接下来,我们可以比较它们的质因数,发现它们没有共有的质因数,即它们的最大公因数是1。
然后,我们可以将它们的质因数相乘,得到它们的最小公倍数,即2×2×2×7=56。
通过质因数分解法,我们得到的结果与之前的计算结果一致,说明这种方法是正确的。
最大公因数和最小公倍数是数学中重要的概念,它们在解决实际问题时起到了重要的作用。
第6讲最大公因数与最小公倍数第一部分知识梳理1.公因数和最大公因数的意义几个数共有的因数,叫作这几个数的公因数;其中最大的一个叫作它们的最大公因数。
2.求公因数和最大公因数的方法(1)列举法:先分别求出两个数的因数,再找出它们的公因数,然后找出最大的一个(2)试除法:先找出较小的那个数的因数,从中找出另一个数的因数,再找出最大的一个。
3.约分的含义及方法含义:把一个分数的分子和分母同时除以它们的公因数,分数的值不变,这个过程叫作约分。
分子和分母只有公因数1的分数,叫作最简分数。
方法:(1)逐次约分法:用分数的分子和分母的公因数(1除外)逐次去除分子和分母,直到得出一个最简分数。
(2)一次约分法:用分数的分子和分母的最大公因数去除分子和分母。
4.公倍数和最小公倍数的意义几个数公有的倍数,叫作这几个数的公倍数。
其中最小的一个叫作最小公倍数。
5.求最小公倍数的方法:(1)列举法:分别写出两个数各自的倍数,再找出它们的公倍数,然后找出最小的一个。
(2)试除法:先找出较大的那个数的倍数,从找出另一个数的倍数,再找出最小的一个。
6.通分的含义方法(1)含义:把几个分母不同的分数化成同分母且分数值保持不变的分数,这个过程叫作通分。
(2)方法:通分时,用原分母的公倍数作为公分母,通常选用最小公倍数作公分母。
7.比较分数大小的方法(1)画图比较法(2)通分比较法(3)同分子比较法第二部分教材解读知识点一公因数和最大公因数的意义知识点二求公因数和最大公因数的方法问题导入找出16和24的公因数和最大公因数知识点三约分的含义知识点四约分的方法知识点五公倍数和最小公倍数的含义知识点六求最小公倍数的方法问题导入求8和10的最小公倍数知识点七比较分数大小的方法知识点八通分的含义和方法第三部分课前热身一、判断题1.5和7没有最大的公因数()2.分子和分母都是偶数的分数,一定不是最简分数()3.分子和分母都是奇数的分数,一定是最简分数()4.最简分数的分子一定小于分母()5.分子和分母是两个不同的质数时,这个分数一定是最简分数()6.分母是8的最简真分数有7个()7.3和6的最小公倍数是12()8.两个不同自然数的最大公因数一定比最小公倍数小()9.两个自然数的乘积一定是这两个自然数的公倍数()10.两个数的最小公倍数一定比这两个数大()11.两个数的最小公倍数一定是这两数的最大公因数的倍数()12.通分时,只能用两个数或几个数分母的最小公倍数作公分母()13.通分的依据是分数的基本性质()14.两个分数通分后,都比原分数大()二、选择题1.既有公因数2,又有公因数3的一组是()A15和6 B 27和28 C12和18 D16和302.最大公因数是1的一组是()A15和5 B11和12 C 38和20 D100和23.甲数是乙数的倍数,甲乙两数的最大公因数是()A1 B甲数C乙数 D 甲乙两数的乘积4.两个数的最大公因数是1,最小公倍数是35,这两个数分别是()A 5和7 B15和20 C 35和5第四部分精讲点拨考点一、用列举法和图解法解决复杂的找最大公因数的问题1.一个长方形,长80dm,宽20dm。
现在把长方形分成若干个正方形,要使正方形的边长尽可能的大,并且长方形的长和宽没有剩余,可以分成多少个正方形?考点二、用列举法解决找三个数的最大公因数的问题2.有三根木棍分别长12cm、18cm和30cm,现在要把他们截成相等的小段,每根不许有剩余,每小段最长是多少?一共可以截成多少段?考点三、用列举法解决复杂的分数问题3.2531的分子和分母同时减去一个数,新的分数约分得34,减去的数是多少?考点四、用找公因数法解决复杂分数的约分问题4.把2005200520052005 2006200620062006约分考点五、用转化法解决稍复杂的最小公倍数问题5.一些小朋友分组做游戏,第一次分组每组4个余下2个,第二次分组每组5个也余下2个,你知道最少有多少个小朋友做游戏?考点六、用画线段图法解决复杂的植树问题6.要在小路一侧种106棵梧桐树,相邻两棵树之间的距离原来是9m,现在要改成相邻两棵树之间的距离是15m,有多少棵树不需要移动?考点七、用“1减”或“减1”的方法解决复杂的分数比较问题7.比较20042005与20052006的大小考点八、用搭桥法解决复杂分数大小比较问题8.比较分数1123和1529的大小第五部分变式练习1.如图,街道ABCD在B,C处拐弯,在街道的一侧要等距离的安装路灯,要求在A,B,C,D处各装一盏路灯。
这条街道最少要安装多少盏路灯?2在一个长30m,宽12m,的长方形池塘的四角和四条边上种树,若相邻两颗树之间的距离相等,最少要种多少棵树?每相邻两棵树之间的距离是多少米?3把15151515152020202020、582317469约成最简分数4.晶晶冲了两杯糖水,第一杯放入10克红糖,60克水。
第二杯放入6克红糖,50克水。
哪杯糖水更甜一些?5.五(1)班在上科学实验课,无论把同学分成2人一组,3人一组或5人一组,都正好分完,五(1)班至少有多少人?6.一排电线杆,原来每两根之间的距离是30m,现在距离要改为45m,如果起点的一根电线杆不移动,至少要隔多远又有一根电线杆不移动?如果这排电线杆共30根,那么有几根不需要移动?7.比较分数3538和6467,2753和4183的大小8.四个分数20082007,20072008,20092008,20082009,其中最大的数是(),最小的数是()。
第六部分过关检测一、填空题:1.如果自然数A除以自然数B商是17,那么A与B的最大公因数是(),最小公倍数是()。
2.最小质数与最小合数的最大公因数是(),最小公倍数是()。
3.能被5、7、16整除的最小自然数是()。
4.5和12的最小公倍数减去()就等于它们的最大公因数。
91和13的最小公倍数是它们最大公因数的()倍。
5.已知两个互质数的最小公倍数是153,这两个互质数是()和()。
6.甲数=2×3×5×7,乙数=2×3×11,甲乙两数的最大公因数是(),最小公倍数是()。
7.3个连续自然数的最小公倍数是60,这三个数是()、()和()。
8.被2、3、5除,结果都余1的最小整数是(),最小三位整数是()。
9.一筐苹果4个4个拿,6个6个拿,或者8个8个拿都正好拿完,这筐苹果最少有()个。
10.三个连续偶数的和是42,这三个数的最大公因数是()。
11.三个不同质数的最小公倍数是105,这三个质数是()、()和()。
12.自然数m和n,n= m+1,m和n的最大公因数是(),最小公倍数是()。
13.把自然数a与b分解质因数,得到a=2×5×7×m,b=3×5×m ,如果a与b的最小公倍数是2730,那么m = ()。
14.三个数的和是312,这三个数分别能被7、8、9整除,而且商相同。
这三个数分别是()、()和()。
15.已知(A,40)=8,[A,40]=80,那么A=()。
二、判断题1.几个数的公倍数是无限的,最小的只有一个.()2.两个不同的自然数的最大公因数一定比最小公倍数小.()3.如果三个自然数两两互质,它们的最大公因数是1,最小公倍数就是三个数的乘积。
()4.如果一个质数与一个合数不是互质数,那么这个合数是这两个数的最小公倍数.()5.一个数的因数必定小于它的倍数.()三、选择题1.96是16和12的()①公倍数②最小公倍数③公因数2.几个质数的连乘积是()①合数②质数③最大公因数④最小公倍数3.甲是乙的15倍,甲和乙的最小公倍数是()①15 ②甲③乙④甲×乙4.12是24和36的()①因数②质因数③最大公因数5.一个数的最大因数()它的最小倍数.①>②<③=6.成为互质数的两个数().①没有公因数②只有公因数1 ③两个数都是质数④都是质因数7.下列各数中与18互质的数是().①21 ②40 ③25 ④188.下列各组数中,两个数互质的是().①17和51 ②52和91 ③24和25 ④ 11和229.甲数的质因数里有1个7,乙数的质因数里没有7,它们的最大公因数的质因数里应该().①有一个7 ②没有7 ③不能确定10.甲、乙两数的最大公约数是7,甲数的3倍与乙数的5倍的最大公约数()①肯定是7 ②肯定不是7 ③不能肯定四、用短除法求下面每组数的最大公因数和最小公倍数。
32和24 12和18 72和4878和39 3、15和20 12、60和183、4和54、8和16五、解决下列的问题:1.有三根铁丝,一根长18米,一根长24米,一根长30米。
现在要把它们截成同样长的小段。
每段最长可以有几米?一共可以截成多少段?2.一张长方形纸,长60厘米,宽36厘米,要把它截成同样大小的长方形,并使它们的面积尽可能大,截完后又正好没有剩余,正方形的边长可以是多少厘米?能截多少个正方形?3.用96朵红玫瑰花和72朵白玫瑰花做花束。
若每个花束里的红玫瑰花的朵数相同,白玫瑰花的朵数也相同,最多可以做多少个花束?每个花束里至少要有几朵花?(1)最多可以做多少个花束(2)每个花束里有几朵红玫瑰花(3)每个花束里有几朵白玫瑰花(4)每个花束里最少有几朵花4.公共汽车站有三路汽车通往不同的地方。
第一路车每隔5分钟发车一次,第二路车每隔10分钟发车一次,第三路车每隔6分钟发车一次。
三路汽车在同一时间发车以后,最少过多少分钟再同时发车?5.某厂加工一种零件要经过三道工序。
第一道工序每个工人每小时可完成3个;第二道工序每个工人每小时可完成12个;第三道工序每个工人每小时可完成5个。
要使流水线能正常生产,各道工序每小时至少安排几个工人最合理?6.有一行数:1,1,2,3,5,8,13,21,34,55……,从第三个数开始,每个数都是前两个数的和,在前100个数中,偶数有多少个?7.一个长方形的长和宽都是自然数,面积是36平方米,这样的形状不同的长方形共有多少种?8.一种长方形的地砖,长24厘米,宽16厘米,用这种砖铺一个正方形,至少需多少块砖?9.一块长方形铁皮,长96厘米,宽80厘米,要把它剪成同样大小的正方形且没有剩余,这种正方形的边长最大是多少?被剪成几块?10.已知某小学六年级学生超过100人,而不足140人。
将他们按每组12人分组,多3人;按每组8人分,也多3人。
这个学校六年级学生多少?11.有四个小朋友,他们的年龄一个比一个大一岁,四个人的年龄的乘积是360。
他们中年龄最大是多少岁?12.汽车站内每隔3分钟发一辆公交车,4分钟发一辆中巴车,1小时共发了几辆汽车?其中有几辆中巴车?13.一块长方形铁皮,长96厘米,宽80厘米,要把它剪成同样大小的正方形且没有剩余,这种正方形的边长最大是多少?被剪成了几块?14.有一个长80厘米,宽60厘米,高115厘米的长方体储冰容器,往里面装入大小相同的立方体冰块,这个容器最少能装多少数量的冰块?。