FR12、 FR32
第21页/共30页
FR32= - FR12= FR21
3).取构件3为分离体——其上作用有:FR23、 FR43、 M3
由力平衡条件得: FR43= - FR23= FR21
M3 = FR23L´
C
FR23
3
L
M3
ω1 1 D
FR43
第22页/共30页
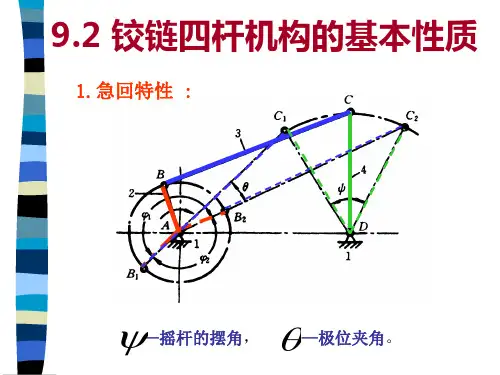
例 如图所示为一曲柄滑块机构,设各构件的尺寸(包括转动副的半径)已知,各
式中
xI, yI——力作用点I的坐标, xK, yK——取矩点K的坐标。
第16页/共30页
4) 各构件的力平衡方程式
•对于构件1分别根据
•对于构件2有
•对于构件3有
可得
第17页/共30页
以上共列出九个方程式,故可解出上述各运动副反力和平衡力的九个力 的未知要素。又因为以上九式为一线性方程组,因此可按构件1、2、3上待 定的未知力Mb, R41x, R41y, R12x, R12y, R23x, R23y, R34x, R34y的次序整理成以下的 矩阵形式:
3求rc取构件3为分离体并取该构件上的诸力对d点取矩规定力矩的方向逆时针者为正顺时针者为负则于是得同理取构件2为分离体并取诸力对b点取矩则因此可得3求rd根据构件3上的诸力平衡条件4求rb根据构件2上的诸力平衡条件5求ra同理根据构件1的平衡条件得至此机构的受力分析进行完毕
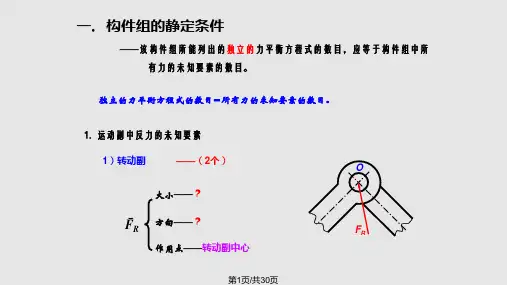
一. 构件组的静定条件
——该构件组所能列出的独立的力平衡方程式的数目,应等于构件组中所 有力的未知要素的数目。
A
ω23
C
FR32
3
M3
4D
解:1).求构件2所受的两力FR12、FR32的方位。
2).取曲柄1为分离体——其上作用有: