全等三角形练习题

全等三角形判定练习题一、选择题1. 在三角形ABC和三角形DEF中，若AB=DE，AC=DF，BC=EF，那么这两个三角形：A. 相似B. 全等C. 不全等D. 无法确定2. 若三角形ABC的角A等于角D，且AB=DE，AC=DF，但BC不等于EF，这两个三角形：A. 相似B. 全等C. 不相似D. 不全等3. 已知三角形ABC与三角形DEF全等，根据SAS（边-角-边）判定，下列选项正确的是：A. AB=DE，BC=EF，角A=角DB. AB=DE，AC=DF，角B=角EA. AB=DE，角A=角D，角B=角ED. AB=DE，角A=角D，角C=角F二、填空题4. 如果三角形ABC与三角形DEF全等，且角A等于角D，角B等于角E，那么角C等于______。

5. 在三角形ABC中，若AB=AC，角A等于角B，根据______判定，三角形ABC是等腰三角形。

6. 如果三角形ABC的边AB等于三角形DEF的边DE，且角A等于角D，角B等于角E，但角C不等于角F，根据______判定，这两个三角形不全等。

三、解答题7. 已知三角形ABC与三角形DEF全等，且AB=DE，角B=角E，求证AC=DF。

8. 在三角形ABC中，已知AB=AC，角A=角B，求证三角形ABC是等腰三角形。

9. 根据SSS（边-边-边）判定，如果三角形ABC的边AB、AC、BC分别等于三角形DEF的边DE、DF、EF，那么这两个三角形是______。

10. 如果三角形ABC的边AB、AC等于三角形DEF的边DE、DF，但角A不等于角D，角B不等于角E，求证这两个三角形不全等。

四、证明题11. 证明：如果三角形ABC的角A等于角D，角B等于角E，且AB+AC=DE+DF，那么三角形ABC与三角形DEF全等。

12. 已知三角形ABC与三角形DEF全等，且角A等于角D，角B等于角E，证明：角C等于角F。

13. 在三角形ABC中，如果角A等于角B，且AB+BC=AC+BC，证明：三角形ABC是等腰三角形。

三角形的全等练习题一、选择题1. 下列哪个条件可以判定两个三角形全等？A. 两边和其中一边的对角相等B. 两角和其中一角的对边相等C. 两边和它们的夹角相等D. 两角和其中一边相等A. △ABC ≌ △DEFB. △ABC ≌ △DFEC. △ABC ≌ △DGED. 无法确定3. 下列哪个条件不能判定两个三角形全等？A. SAS（边角边）B. ASA（角边角）C. AAS（角角边）D. SSS（三边）二、填空题1. 若△ABC和△DEF全等，其中AB=DE，BC=EF，则∠A=______，∠B=______。

2. 在△ABC中，AB=AC，∠B=40°，则∠C=______。

3. 若△ABC和△DEF全等，且∠A=∠D，AB=DE，则全等三角形对应边为：BC=______，AC=______。

三、判断题1. 两个等腰三角形的底边和腰长分别相等，则这两个三角形全等。

（）2. 两个三角形有两边和它们的夹角分别相等，则这两个三角形全等。

（）3. 两个三角形的三个角分别相等，则这两个三角形全等。

（）四、作图题1. 请画出一个等腰三角形，并标出其底边和高。

2. 请画出两个全等的直角三角形，并标出它们的对应边和对应角。

五、解答题1. 在△ABC中，AB=AC，∠B=60°，求∠A和∠C的度数。

2. 已知△ABC和△DEF全等，其中AB=DE，BC=EF，∠B=∠E，求∠A、∠C、∠D和∠F的度数。

3. 在△ABC中，∠A=40°，∠B=70°，∠C=70°，求证：△ABC是一个等腰三角形。

六、应用题1. 在一块三角形菜地中，已知两边的长度分别为15米和20米，夹角为60°，请计算这块三角形菜地的面积。

2. 两个相同的等腰三角形模型，底边长为10厘米，腰长为13厘米，将它们拼成一个平行四边形，求这个平行四边形的周长。

3. 有一块三角形玻璃，其两个角的度数分别为45°和45°，斜边长为6厘米。

全等三角形练习题一、选择题：1. 在三角形ABC中，如果AB=AC，且角BAC=80°，则角B的度数为多少？A. 50°B. 80°C. 100°D. 无法确定2. 已知三角形ABC与三角形DEF全等，且AB=DE，角A=角D，那么AC 与DF的关系是什么？A. AC=DFB. AC>DFC. AC<DFD. 无法确定3. 如果三角形ABC与三角形DEF全等，且角BAC=角EDF，角ABC=角DEF，那么AB与DE的关系是什么？A. AB=DEB. AB>DEC. AB<DED. 无法确定二、填空题：1. 在三角形ABC中，如果AB=AC，角BAC=50°，那么角ABC的度数为______。

2. 如果三角形ABC与三角形DEF全等，且角A=角D，角B=角E，那么角C与角F的关系是______。

3. 已知三角形ABC的周长为180cm，AB=50cm，AC=60cm，那么BC的长度为______。

三、解答题：1. 已知三角形ABC中，AB=13cm，AC=15cm，角BAC=120°。

求BC的长度。

2. 已知三角形ABC与三角形DEF全等，AB=DE，角B=角E，BC=EF。

如果AC=14cm，求DF的长度。

3. 已知三角形ABC中，AB=10cm，AC=12cm，角BAC=60°。

求角B的度数。

四、证明题：1. 已知三角形ABC与三角形DEF全等，AB=DE，角A=角D，证明AC=EF。

2. 已知三角形ABC中，AB=AC，角BAC=80°，证明三角形ABC是等腰三角形。

3. 已知三角形ABC与三角形DEF全等，且角BAC=角EDF，角ABC=角DEF，证明三角形ABC与三角形DEF是全等三角形。

五、应用题：1. 一个等腰三角形的底边长为10cm，高为6cm，求这个等腰三角形的面积。

2. 一个等边三角形的边长为8cm，求这个等边三角形的高。

1、如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；求证：BC=DC．2、如图，△ABC与△DCB中，AC与BD交于点E，且∠A=∠D，AB=DC．（1）求证：△ABE≌DCE；（2）当∠AEB=50°，求∠EBC的度数？3、如图，点B、F、C、E在一条直线上，FB=CE，AB∥ED，AC∥FD，求证：AC=DF4、如图，点E、F在BC上，BE=FC，AB=DC，∠B=∠C．求证：∠A=∠D．5、如图，∠AOB=90°，OA=OB，直线l经过点O，分别过A、B两点作AC⊥l交l 于点C，BD⊥l交l于点D．求证：AC=OD．6、如图，已知AD是△ABC的中线，分别过点B、C作BE⊥AD于点E，CF⊥AD交AD的延长线于点F，求证：BE=CF．7、如图，已知点B、E、C、F在同一条直线上，BE=CF，AB∥DE，∠A=∠D．求证：AB=DE．8、如图，CD=CA，∠1=∠2，EC=BC，求证：DE=AB9、如图，点D是△ABC的边AB上一点，点E为AC的中点，过点C作CF∥AB交DE延长线于点F．求证：AD=CF10、如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置．F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H．（1）求证：CF=DG；（2）求出∠FHG的度数．11、如图，C是AB的中点，AD=BE，CD=CE．求证：∠A=∠B．12、已知：如图，D是AC上一点，AB=DA，DE∥AB，∠B=∠DAE．求证：BC=AE．13、已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．14、如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF=∠ADF．（1）求证：△ADE≌△BFE；（2）连接EG，判断EG与DF的位置关系并说明理由．15、在数学课上，林老师在黑板上画出如图所示的图形（其中点B、F、C、E在同一直线上），并写出四个条件：①AB=DE，②BF=EC，③∠B=∠E，④∠1=∠2．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．题设：；结论：。

三角形的全等练习题一、选择题：1. 两个三角形全等的条件是（）A. 三边对应相等B. 两边加一角对应相等A. 两角一边对应相等D. 一边一角对应相等2. 若三角形ABC与三角形DEF全等，且AB=DE，AC=DF，以下哪个条件能确保∠A=∠D？A. ∠B=∠EB. ∠C=∠FC. ∠A=∠DD. ∠BAC=∠FED3. 在三角形中，若∠A=∠B+∠C，那么三角形ABC是（）A. 直角三角形B. 等腰三角形C. 等边三角形D. 钝角三角形4. 三角形全等的判定定理中，SAS表示（）A. 三边对应相等B. 两边加夹角对应相等C. 两角加一边对应相等D. 一边加两角对应相等5. 若三角形ABC与三角形DEF全等，且∠A=∠D，∠B=∠E，AB=DE，以下哪个条件不能推出三角形全等？A. BC=EFB. AC=DFC. ∠C=∠FD. ∠BAC=∠FED二、填空题：6. 若三角形ABC与三角形DEF全等，且AC=DF，∠A=∠D，那么根据______判定定理，可以得出三角形ABC与三角形DEF全等。

7. 在三角形ABC中，若AB=AC，∠A=80°，则∠B=∠C=______。

8. 若三角形ABC与三角形DEF相似，且AB/DE=2/3，那么根据相似三角形的性质，BC/EF=______。

9. 在直角三角形ABC中，若∠C=90°，AB=10，AC=8，则BC的长度为______。

10. 三角形的内角和为______度。

三、解答题：11. 已知三角形ABC与三角形DEF全等，且AB=DE，∠A=∠D，证明：AC=DF。

12. 在三角形ABC中，若AB=5，AC=7，BC=6，求证：三角形ABC是直角三角形。

13. 已知三角形ABC与三角形DEF相似，且AB/DE=2，求证：AC/DF=2。

14. 在三角形ABC中，若∠A=60°，∠B=40°，求∠C的度数。

15. 若三角形ABC的周长为24，且AB=5，AC=7，求BC的长度。

全等三角形的性质专项练习30题（有答案）1．如图，点A，B，C，D在一条直线上，△ABF≌△DCE．你能得出哪些结论？（请写出三个以上的结论）2．如图，△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，求∠DFB和∠DGB的度数．3．如图，AB=DC，AC=DB，你能说明图中∠1=∠2的理由吗？4．已知：AB=DE，AF=CD，∠A=∠D，EF=BC，试说明：BF∥CE．5．已知△ABC≌△DEF，其中AB=2cm，BC=3cm，AC=4cm，则△DEF的三边长DE=_________cm，EF= _________cm，DF=_________cm．6．如图，△ABC≌△ADE，∠B=40°，∠E=30°，∠BAE=80°，求∠BAC、∠DAC的度数．7．如图，△AOC≌△BOD，试证明AC∥BD．8．如图，△ABC≌△DEF，∠A=25°，∠B=65°，BF=3cm，求∠DFE的度数和EC的长．9．如图，△ABD≌△EBD，△DBE≌△DCE，B，E，C在一条直线上．（1）BD是∠ABE的平分线吗？为什么？（2）DE⊥BC，BE=EC吗？为什么？10．附加题：如图△ABC≌△DBC，∠A=110°，则∠D=_________．11．如图，已知△AEC≌△BFD，则AD_________BC．（填“＞”、“=”或“＜”）．12．如图，△ABC≌△DEC，∠A：∠ABC：∠BCA=3：5：10，（1）求∠D的度数；（2）求∠EBC的度数．13．如图，△ABN≌△ACM，∠B和∠C是对应角，AB与AC是对应边，写出其他对应边和对应角．14．如图，已知△ABD≌△ACE．求证：BE=CD．15．如图，△ABC≌△DEF，BF=3，EF=2．求FC的长．16．如图，△ABC≌△BDE，M、M′分别为AB、DB中点，直线MM′交CE于K．试探索CK与EK的数量关系．17．如图，在△ABC中，BE，CF分别是AC，AB边上的高线，BE，CF相交于O，连接AO交BC于D，且△BCF≌△CBE，∠ABC=70°，求∠1和∠2的度数．18．如图，已知△ABC≌△ADE，BC的边长线交AD于F，交AE于G，∠ACB=105°，∠CAD=10°，∠ADE=25°，求∠DFB和∠AGB的度数．19．如图，△ABC≌△DEC，∠1与∠2相等吗？请说明理由．20．如图，△ABC≌△EBD．求证：∠1=∠2．21．如图，△ABC≌△ADE，∠CAD=10度，∠B=∠D=25度，∠EAB=120度，试求∠ACB的度数．22．如图，△ABC≌△DEF，△ABC的周长是40cm，AB=10cm，BC=16cm，求△DEF中，边DF的长度．23．如图：△ABF≌△DCE，写出相等的线段．24．如图，△ABC≌△ADE中，BA⊥AE，∠BAC=30°，AD=5，求BD的长．25．如右图所示，已知△ABD≌△ACE，试说明BE=CD．26．如图，△ABC≌△EFD，你能从图中找到几组平行线？请写出，并选择一组说明理由．27．如图，点B、E、C、F在一条直线上，BC=EF AB∥DE，请你添加一个条件_________，使△ABC≌△DEF．并写出证明过程．28．如图，△ACF≌△DBE，∠E=∠F，若AD=11，BC=7，求线段AB的长．29．如图，已知△ABC≌△DEF，∠A=30°，∠B=50°，BF=2，求∠DFE的度数和EC的长．30．如图，△ABC≌△ADE，B点的对应顶点是D点，若∠BAD=100°，∠CAE=40°，求∠BAC的度数．参考答案1．∵△ABF≌△DCE∴∠BAF=∠CDE，∠AFB=∠DEC，∠ABF=∠DCE，AB=DC，BF=CE，AF=DE；∴AF∥ED，AC=BD，BF∥CE．2．∵△ABC≌△ADE，∴∠DAE=∠BAC=（∠EAB﹣∠CAD）=．∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°∠DGB=∠DFB﹣∠D=90°﹣25°=65°3．证明：在△ABC和△DCB中，AB=DC，AC=DB，BC=BC，∴△ABC≌△DCB（SSS），∴∠1=∠2．4．∵AB=DE，AF=CD，∠A=∠D，则可得△ABF≌△DEC，∴BF=EC，又EF=BC，∴可得四边形BCEF是平行四边形，∴BF∥EC5．∵△ABC≌△DEF∴AB=DE，BC=EF，AC=DF∴DE=2cm，EF=3cm，DF=4cm．6．①∵△ABC≌△ADE，∴∠B=∠D=40°，∠E=∠C=30°，∴∠BAC=180°﹣∠B﹣∠C=110°；②∵∠BAE=80°，∠BAC=∠DAE=110°∴∠BAD=∠DAE﹣∠BAE=30°，∴∠DAC=∠BAC+∠BAD=110°+30°=140°7.∵△AOC≌△BOD，∴∠A=∠B（全等三角形对应角相等）．∴AC∥BD（内错角相等，两直线平行）8．△ABC中∠A=25°，∠B=65°，∴∠BCA=180°﹣∠A﹣∠B=180°﹣25°﹣65°=90°，∵△ABC≌△DEF，∴∠BCA=∠DFE，BC=EF，∴EC=BF=3cm．∴∠DFE=90°，EC=3cm．9．（1）∵△ABD≌△EBD，∴∠ABD=∠EBD，∴BD是∠ABE的平分线；（2）∵△DBE≌△DCE，∴∠DEB=∠DEC，∵∠DEB+∠DEC=180°，∴∠DEB=∠DEC=90°，∴DE⊥BC，∵△DBE≌△DCE，∴BE=EC．10．解：∵△ABC≌△DBC，∠A=110°∴∠D=∠A=110°．11．∵△AEC≌△BFD∴AC=BD（全等三角形对应边相等）∴AC+CD=BD+CD，即AD=BC．12．（1）∵∠A+∠ABC+∠BCA=180°，∠A：∠ABC：∠BCA=3：5：10，∴∠A=180°×=30°，∠ABC=180°×=50°，∠BCA=180°×=100°，又∵△ABC≌△DEC，∴∠D=∠A=30°；（2）∵△ABC≌△DEC，∴∠E=∠ABC=50°，∵∠BCA=100°，∴∠EBC=∠BCA﹣∠E，=100°﹣50°=50°13．∵△ABN≌△ACM，∠B和∠C是对应角，AB与AC是对应边，∴对应边：AN与AM，BN与CM；对应角：∠BAN=∠CAM，∠ANB=∠AMC14．∵△ABD≌△ACE，∴AB=AC，AD=AE，∴AC﹣AD=AB﹣AE，即CD=BE15．∵△ABC≌△DEF∴BC=EF=2又∵FC=BF﹣BC∴FC=3﹣2=116．CK与EK的数量关系为相等，理由如下：延长MK到N，使得NK=MM'，连接EM′、CM、EN，如图，可得NK+KM'=MM'+M'K，即NM'=MK，∵△ABC≌△BDE，M、M′分别为AB、DB中点，∴EM'=CM，BM'=BM，∠EM'D=∠CMB，由BM'=BM得：∠BM'M=∠BMM'=∠KM'D，∴∠NM'E=∠CMK，在△EM'N和△CMK中，NM'=MK，∠NM'E=∠CMK，EM'=CM，∴△EM'N≌△CMK，（SAS）∴CK=EN，∠N=∠CKM=∠NKE，∴EK=EN，∴CK=EK．17．∵△BCF≌△CBE，∴∠FBC=∠ECB=70°，∴∠BAC=180°﹣∠FBC﹣∠ECB=40°，AB=AC，∵BE，CF分别是AC，AB边上的高线，BE，CF相交于O，∵AD⊥BC，∴∠1=∠2=∠BAC=20°18．∵△ABC≌△ADE，∴∠ACB=∠AED，∠ABC=∠ADE，∠CAB=∠EAD．∵∠ADE=25°，∴∠ABC=∠ADE=25°．∵∠ACB=105°，∴∠CAB=180°﹣105°﹣25°=50°．∴∠DFB=∠DAB+∠ABC=50°+10°+25°=85°．∠AGB=∠ACB﹣∠GAC=105°﹣50°﹣10°=45°19．由题意：∵△ABC≌△DEC，∴BC=EC．∴∠1=∠220．∵△ABC≌△EBD．∴∠A=∠E．又∵∠AOD=∠BOE，∴∠A+∠AOD+∠1=∠E+∠BOE+∠2=180°，∴∠1=∠221．∵△ABC≌△ADE，∴∠CAB=∠EAD．∵∠EAB=120°，∠CAD=10°，∴∠EAB=∠EAD+∠CAD+∠CAB=2∠CAB+10°=120°，∴∠CAB=55°．∵∠B=∠D=25°，∴∠ACB=180°﹣∠CAB﹣∠B=180°﹣55°﹣25°=100°，即∠ACB的度数是100°22．已知，△ABC的周长是40cm，AB=10cm，BC=16cm，∴AC=△ABC的周长﹣AB﹣BC=40﹣10﹣16=14（cm），∵△ABC≌△DEF，∴DF=AC=14cm，所以边DF的长度为14cm23．∵△ABF≌△DCE，∴AB=DC，BF=CE，AF=DE，∠DEC=∠AFE，∴OE=OF，∴AF﹣FO=DE﹣OE，∴AO=DO，∵BF=CE，∴BF﹣FE=CE﹣EF，∴EB=FC．24．由题意得：∠BAC=∠DAE=30°，AB=AD，∠BAE=90°，∴∠CAD=30°，∴∠ABD=60°，∴△ABD是等边三角形．故可得：BD=AD=525．∵△ABD≌△ACE，∴AD=AE，AC=AB，∴AE﹣AB=AD﹣AC，即BE=CD26．AB∥EF，AC∥ED．∵△ABC≌△EFD，∴∠B=∠F，∠ACB=∠EDF，∴AB∥EF，AC∥ED27．∠ACB=∠F或AB=DE或∠A=∠D．以下证明添加条件为AB=DE时，△ABC≌△DEF．∵AB∥DE，∴∠B=∠DEF．在△ABC和△DEF中，∴△ABC≌△DEF28．∵△ACF≌△DBE，∴AC=DB，∴AC﹣BC=DB﹣BC，即AB=CD，∵AD=11，BC=7，∴AB=（AD﹣BC）=（11﹣7）=2即AB=229．∵∠A=30°，∠B=50°，∴∠ACB=180°﹣∠A﹣∠B=180°﹣30°﹣50°=100°，∵△ABC≌△DEF，∴∠DFE=∠ACB=100°，EF=BC，∴EF﹣CF=BC﹣CF，即EC=BF，∵BF=2，∴EC=230．∵△ABC≌△ADE，∴∠BAC=∠DAE，∴∠BAC﹣∠CAE=∠DAE﹣∠CAE，即∠BAE=∠DAC，∵∠BAD=100°，∠CAE=40°，∴∠BAE=（∠BAD﹣∠CAE）=（100°﹣40°）=30°，∴∠BAC=∠BAE+∠CAE=30°+40°=70。

全等三角形的练习题及答案1、下列判定直角三角形全等的方法，不正确的是A、两条直角边对应相等。

B、斜边和一锐角对应相等。

C、斜边和一条直角边对应相等。

D、两锐角相等。

2、在△ABC中，∠B＝∠C，与△ABC全等的三角形有一个角是100°，那么在△ABC中与这100°角对应相等的角是A.∠AB.∠BC.∠CD.∠B或∠C3、下列各条件中，不能作出唯一三角形的是A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角 D.已知三边4、在△ABC与△DEF中，已知AB=DE；∠A=∠D；再加一个条件，却不能判断△ABC与△DEF全等的是.A． BC=EF B．AC=DFC．∠B=∠E D．∠C=∠F5、使两个直角三角形全等的条件是A．一锐角对应相等 B．两锐角对应相等C．一条边对应相等 D．两条直角边对应相等6、在△ABC和△A’B’C’中有①AB=A’B’，②BC=B’C’，③AC=A’C’，④∠A=∠A’，⑤∠B=∠B’，⑥∠C=∠C’，则下列各组条件中不能保证△ABC≌△A’B’C’的是A、①②③B、①②⑤C、①②④D、②⑤⑥7、如图，已知∠1=∠2，欲得到△ABD≌△ACD，还须从下列条件中补选一个，错误的选法是A、∠ADB=∠ADCB、∠B=∠CC、DB=DCD、AB=AC8、如图，△ABC≌△ADE，若∠BAE=120°，∠BAD=40°，则∠B AC的度数为A.0°B.0°C.120°D. 不能确定9、如图，AE＝AF，AB＝AC，EC与BF交于点O，∠A ＝60，∠B＝25，则∠EOB的度数为00A．60 B．70 C．75D．8510、如图，已知AB＝DC，AD＝BC，E.F在DB上两点且BF＝DE，若∠AEB＝120°，∠ADB＝30°，则∠BCF=A. 150°B.40°C.80°D. 0° 0000 11、①两角及一边对应相等②两边及其夹角对应相等③两边及一边所对的角对应相等④两角及其夹边对应相等，以上条件能判断两个三角形全等的是A．①③ B．②④C．②③④D．①②④12、下列条件中，不能判定两个三角形全等的是A．三条边对应相等B．两边和一角对应相等C．两角及其一角的对边对应相等D．两角和它们的夹边对应相等13、如图，已知，，下列条件中不能判定⊿≌⊿的是∥14、如图，AB与CD交于点O，OA＝OC，OD＝OB，∠A=50°，∠B＝30°，则∠D的度数为.A．50°B．30°C．80°D．100°15、如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD 与BE相交于点F，若BF＝AC，则∠ABC的度数是．16、在△ABC和△中，∠A=44°，∠B=67°，∠=69°，∠=44°，且AC=则这两个三角形全等17、如图,,,,在同一直线上，，，若要使，则还需要补充一个条件：或．18、如图，已知∠CAB=∠DBA，要使△ABC≌△BAD，需增加的一个条件是。

三角形全等的练习题一、选择题1. 在三角形ABC中，若AB=AC，且∠BAC=80°，则∠B的度数是：A. 50°B. 80°C. 100°D. 40°2. 已知两个三角形的三边对应相等，这两个三角形：A. 一定相似B. 一定全等C. 可能全等D. 可能相似3. 若三角形的两边及其夹角与另一个三角形的两边及其夹角相等，则这两个三角形：A. 一定全等B. 一定相似C. 不一定全等D. 不一定相似4. 根据SSS（边边边）全等条件，下列哪组三角形全等：A. △ABC和△DEF，AB=DE，BC=EF，AC=DFB. △ABC和△DEF，AB=DE，∠B=∠D，AC=DFC. △ABC和△DEF，AB=DE，∠A=∠D，BC=EFD. △ABC和△DEF，∠A=∠D，∠B=∠E，∠C=∠F5. 如果两个三角形的两组对应边分别相等，且它们的夹角不相等，那么这两个三角形：A. 全等B. 相似C. 不全等D. 不相似二、填空题6. 在三角形ABC中，如果AB=AC，BC=BD，且∠ABC=∠CBD=60°，则三角形ABC是________。

7. 根据AAS（角角边）全等条件，如果两个三角形的两个角和它们之间的一边对应相等，那么这两个三角形________。

8. 如果三角形ABC的边长分别为AB=5，AC=7，BC=6，那么三角形ABC 是________。

9. 在三角形ABC中，如果∠A=90°，AB=3，AC=4，那么BC的长度是________。

10. 如果两个三角形的对应角相等，且它们的对应边的比相等，那么这两个三角形________。

三、简答题11. 解释ASA（角边角）全等条件，并给出一个例子。

12. 如果两个三角形的一边和这条边的两个相邻角对应相等，这两个三角形是否全等？为什么？13. 描述SAS（边角边）全等条件，并给出一个应用场景。

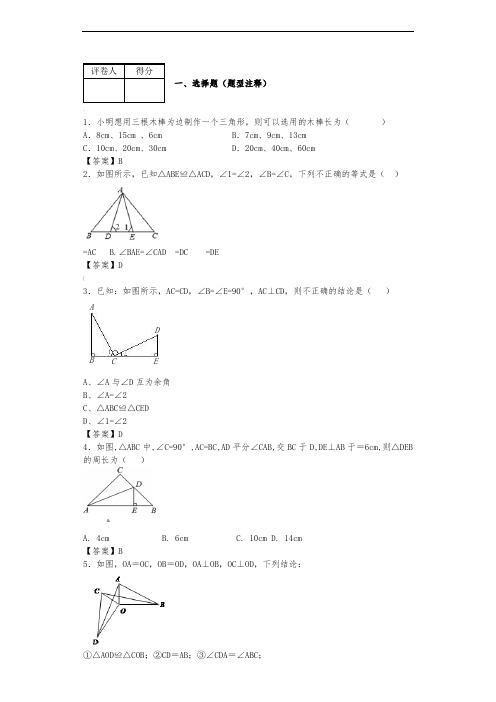
评卷人得分一、选择题（题型注释）、1．小明想用三根木棒为边制作一个三角形，则可以选用的木棒长为（）A．8cm、15cm 、6cm B．7cm、9cm、13cmC．10cm、20cm、30cm D．20cm、40cm、60cm【答案】B2．如图所示，已知△ABE≌△ACD，∠1=∠2，∠B=∠C，下列不正确的等式是（）=AC B.∠BAE=∠CAD =DC =DE【答案】D[3．已知：如图所示，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（）A、∠A与∠D互为余角B、∠A=∠2C、△ABC≌△CEDD、∠1=∠2【答案】D4．如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于＝6cm,则△DEB 的周长为（）A. 4cmB. 6cmC. 10cmD. 14cm【答案】B5．如图，OA＝OC，OB＝OD，OA⊥OB，OC⊥OD，下列结论：①△AOD≌△COB；②CD＝AB；③∠CDA＝∠ABC；&AB CDE1]其中正确的结论是( )A．①② B．①②③ C．①③ D．②③》【答案】B【解析】试题分析：因为OA＝OC，OB＝OD，OA⊥OB，OC⊥OD，可得△COD≌△AOB, ∠CDO＝∠ABO；∠DOC+∠AOC=∠AOB+∠AOC, OA＝OC，OB＝OD,所以△AOD≌△COB，所以CD＝AB,∠ADO=∠CBO；所以∠CDA＝∠ABC.故①②③都正确.故选B考点：三角形全等的判定和性质6．如图，△ABC中，∠B=∠C，BD=CF，BE=CD，∠EDF=α，则下列结论正确的是（）…A．2α+∠A=180° B．α+∠A=90° C．2α+∠A=90° D．α+∠A=180°【答案】A【解析】试题分析：根据已知条件可证明△BDE≌△CFD，则∠BED=∠CDF，由∠A+∠B+∠C=180°，得∠B=，因为∠BDE+∠EDF+∠CDF=180°，所以得出a与∠A的关系2a+∠A=180°．考点：全等三角形的判定和性质，三角形的内角和定理7．如图，AD是△ABC的中线，E、F分别在AB、AC上，且DE⊥DF，则（）~A．BE+CF＞EFB．BE+CF=EFC．BE+CF＜EFD．BE+CF与EF的大小关系不能确定．【答案】A．8．如图，△ABC中边AB的垂直平分线分别交BC，AB于点D，E，AE=3cm，△ADC的周长为9cm，则△ABC的周长是（）A．10cm B．12cm C．15cm D．17cm}【答案】C．【解析】试题分析：∵AB的垂直平分AB，∴AE=BE，BD=AD，∵AE=3cm，△ADC的周长为9cm，∴△ABC的周长是9cm+2×3cm=15cm，故选C．考点：线段垂直平分线的性质．9．如图所示，∠A+∠B+∠C+∠D+∠E的结果为（）A．90° B．1 80° C．360° D．无法确定【答案】?【解析】试题分析：延长BE交AC于F，∵∠A+∠B=∠2，∠D+∠E=∠1，∠1+∠2+∠C=180°，∴∠A+∠B+∠C+∠D+∠E=180°，考点：1．三角形内角和定理；2．三角形的外角性质．10．若△ABC中，2（∠A+∠C）=3∠B，则∠B的外角度数为何（）>A、36B、72C、108D、144【答案】C【解析】∵∠A+∠B+∠C=180°，∴2（∠A+∠B+∠C）=360°，∵2（∠A+∠C）=3∠B，∴∠B=72°，11．如图，AB∥CD，∠D =∠E =35°，则∠B的度数为（）.A．60° B．65° C．70° D．75°【答案】C.~12．如图，已知△ABC，O是△ABC内的一点，连接OB、OC，将∠ABO、∠ACO分别记为∠1、∠2，则∠1、∠2、∠A、∠O四个角之间的数量关系是（）A ．∠1+∠0=∠A+∠2B ．∠1+∠2+∠A+∠O=180°C ．∠1+∠2+∠A+∠O=360°D ．∠1+∠2+∠A=∠O【答案】D ．【解析】 试题分析：连接AO 并延长，交BC 于点D ，》∵∠BOD 是△AOB 的外角，∠COD 是△AOC 的外角，∴∠BOD=∠BAD+∠1①，∠COD=∠CAD+∠2②，①+②得，∠BOC=（∠BAD+∠CAD ）+∠1+∠2，即∠BOC=∠BAC+∠1+∠2．故选D ．考点：1．三角形的外角性质；2．三角形内角和定理．13．如图，BD 是∠ABC 的角平分线，DE ⊥AB 于E ，DF ⊥BC 于F ，，，，△cm 12BC cm 18AB cm 362ABC ===S 则DE 的长是（ ）B.cm 512 D.cm 514 ￥【答案】B【解析】试题分析：∵BD 是∠ABC 的角平分线，DE ⊥AB ，DF ⊥BC,由角平分线的性质可得DE=DF ∴DCB S S ∆∆+=ADB ABC S △=DF DE ⋅⨯+⋅⨯12211821=9DE+6DF=15DE=36∴DE=cm 512 所以选B.考点：角平分线的性质？第II卷（非选择题）请点击修改第II卷的文字说明评卷人得分~二、填空题（题型注释）14．如图，△ABC中，∠A＝90°，DE是BC的垂直平分线，AD=DE，则∠C的度数是°．【答案】30°．【解析】试题分析：∵DE是BC的垂直平分线，∴DE⊥BC，∵∠A＝90°，AD=DE，∴BD平分∠AABC，∴∠ABD=∠DBC，∵DE是BC的垂直平分线，∴DC=BD，∴∠C=∠DBC，∴3∠C=90°，∴∠C=30°．故答案为：30°．考点：1．线段垂直平分线的性质；2．角平分线的性质．!15．如图，在△ABC中，∠ACB＝90°，AB的垂直平分线DE交AB于E，交AC于D，∠DBC＝30°，BD＝，则D到AB的距离为。

全等三角形性质练习题一、选择题1. 两个三角形的对应边相等，那么这两个三角形一定是：A. 相似三角形B. 全等三角形C. 不相似三角形D. 不全等三角形2. 如果两个三角形的对应角相等，那么这两个三角形：A. 一定是全等三角形B. 可能是相似三角形C. 一定是相似三角形D. 无法确定3. 根据SSS（边边边）全等条件，下列哪组三角形是全等的？A. 三边长度分别为3, 4, 5的三角形B. 三边长度分别为5, 12, 13的三角形C. 三边长度分别为6, 8, 10的三角形D. 三边长度分别为7, 24, 25的三角形4. 根据SAS（边角边）全等条件，下列哪组三角形是全等的？A. 两边长度分别为3, 4，夹角为90°的三角形B. 两边长度分别为5, 6，夹角为60°的三角形C. 两边长度分别为7, 8，夹角为45°的三角形D. 两边长度分别为9, 10，夹角为30°的三角形5. 根据ASA（角角边）全等条件，下列哪组三角形是全等的？A. 两角分别为45°, 45°，夹边长度为5的三角形B. 两角分别为30°, 60°，夹边长度为6的三角形C. 两角分别为90°, 45°，夹边长度为7的三角形D. 两角分别为60°, 90°，夹边长度为8的三角形二、填空题6. 如果三角形ABC与三角形DEF全等，那么AB____DE，∠A____∠D，BC____EF。

7. 如果三角形的两边及其夹角与另一个三角形的两边及其夹角对应相等，那么这两个三角形是______。

8. 已知三角形ABC中，AB=5，AC=7，∠A=60°，若三角形DEF与三角形ABC全等，且DE=7，DF=5，则∠D的度数是______。

9. 如果两个三角形的三边对应成比例，那么这两个三角形是______。

10. 在三角形ABC中，如果∠B=∠C，且AB=AC，那么三角形ABC是______三角形。

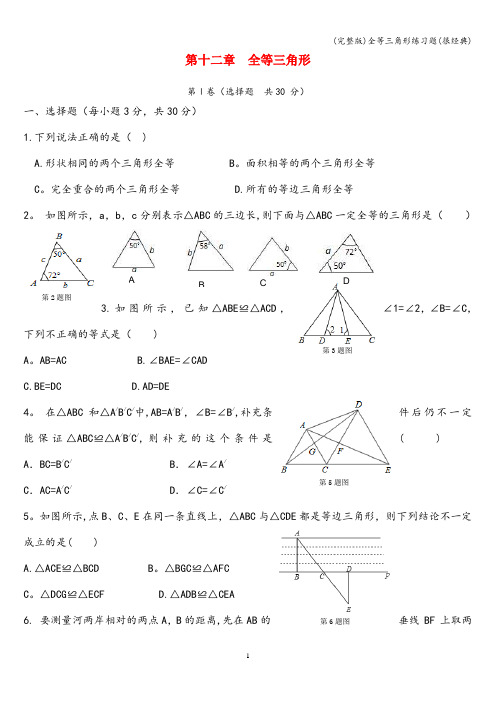
第十二章 全等三角形第Ⅰ卷（选择题 共30 分）一、选择题（每小题3分，共30分） 1.下列说法正确的是（ )A.形状相同的两个三角形全等 B 。

面积相等的两个三角形全等 C 。

完全重合的两个三角形全等 D.所有的等边三角形全等2。

如图所示，a ，b ，c 分别表示△ABC 的三边长,则下面与△ABC 一定全等的三角形是（ ）3.如图所示，已知△ABE≌△ACD ，∠1=∠2，∠B=∠C，下列不正确的等式是（ )A 。

AB=AC B.∠BAE=∠CAD C.BE=DC D.AD=DE4。

在△ABC 和△A /B /C /中,AB=A /B /，∠B=∠B /,补充条件后仍不一定能保证△ABC≌△A /B /C /,则补充的这个条件是( )A ．BC=B /C / B ．∠A=∠A / C ．AC=A /C /D ．∠C=∠C /5。

如图所示,点B 、C 、E 在同一条直线上，△ABC 与△CDE 都是等边三角形，则下列结论不一定成立的是( )A.△ACE≌△BCD B。

△BGC≌△AFC C 。

△DCG≌△ECF D.△ADB≌△CEA 6. 要测量河两岸相对的两点A ，B 的距离,先在AB 的垂线BF 上取两第3题图第5题图第2题图第6题图ABCD点C,D ，使CD=BC ，再作出BF 的垂线DE,使A,C ，E 在一条直线上（如图所示），可以说明△EDC≌△ABC，得ED=AB ，因此测得ED 的长就是AB 的长，判定△EDC≌△ABC 最恰当的理由是（ ）A.边角边 B 。

角边角 C 。

边边边 D 。

边边角7。

已知：如图所示，AC=CD ，∠B=∠E=90°，AC⊥CD,则不正确的结论是( ）A ．∠A 与∠D 互为余角B ．∠A=∠2C ．△ABC≌△CED D．∠1=∠28. 在△ABC 和△FED 中,已知∠C=∠D,∠B=∠E，要判定这两个三角形全等，还需要条件（ ） A 。

全等三角形练习题（打印版）### 全等三角形练习题#### 一、选择题1. 下列选项中，哪两个三角形是全等的？- A. △ABC与△DEF，因为AB=DE，AC=DF，BC=EF- B. △ABC与△DEF，因为∠A=∠D，∠B=∠E，∠C=∠F- C. △ABC与△DEF，因为AB=DE，∠A=∠D，∠B=∠E- D. △ABC与△DEF，因为AB=DE，BC=EF，∠A=∠D2. 根据SSS（边边边）全等条件，下列哪些条件能够判断两个三角形全等？- A. 三边长度相等- B. 两边及夹角相等- C. 一边及其对角相等- D. 两角及一边相等#### 二、填空题1. 如果△ABC与△DEF全等，且AB=DE，AC=DF，那么BC=______。

2. 根据AAS（角角边）全等条件，如果两个三角形的两个角和其中一角的对边相等，那么这两个三角形是______的。

#### 三、判断题1. 如果两个三角形的对应边成比例，那么这两个三角形一定是全等的。

（）2. SAS（边角边）全等条件是判定两个三角形全等的有效条件。

（）#### 四、简答题1. 解释什么是HL（直角三角形的斜边和一条直角边相等）全等条件，并给出一个例子。

2. 描述如何使用SAS全等条件来判断两个三角形是否全等。

#### 五、应用题1. 在△ABC中，已知AB=5cm，AC=4cm，BC=6cm。

在△DEF中，DE=7cm，DF=6cm，EF=5cm。

判断这两个三角形是否全等，并说明理由。

2. 如果△ABC与△DEF全等，且∠A=∠D=90°，AB=DE，AC=DF，求证BC=EF。

#### 六、证明题1. 已知△ABC与△DE F全等，且∠A=∠D，∠B=∠E，AB=DE。

证明AC=DF。

2. 证明：如果两个三角形的三边对应成比例，那么这两个三角形的对应角也相等。

注意：请在解答题目时，确保使用正确的数学符号和清晰的逻辑表达。

练习题的答案应简洁明了，避免冗长和不必要的解释。

全等三角形50道练习题1. B??ABC??DC? ??ACB??DBC ?BC?B C?∴△ABC≌△DCB∴AB=DC3. 如图，点D，E分别在AC，AB上．已知，BD=CE，CD=BE，求证：AB=AC；分别将“BD=CE”记为①，“CD=BE” 记为②，“AB=AC”记为③．添加条件①、③，以②为结论构成命题1，添加条件②、③以①为结论构成命题2．命题1是命题2的命题，命题2是命题．．连结BC，∵ BD=CE，CD=BE，BC=CB．1∴ △DBC≌△ECB∴ ∠DBC =∠ECB∴AB=AC逆，假；4. 如图，在□ABCD中，分别延长BA，DC到点E，使得AE=AB，CH=CD，连接EH，分别交AD，BC于点F,G。

求证：△AEF≌△CHG.证明：∵ □ABCD∴ AB=CD,∠BAD=∠BCD AB∥CD∴ ∠EAF=∠HCG ∠E=∠H∵ AE=AB，CH=CD∴ AE=CH∴ △AEF≌△CHG.5. 如图，点A、F、C、D在同一直线上，点B和点E 分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．求证：BC∥EF．∵AF＝DC，∴AC＝DF，又∠A＝∠D ，AB＝DE，∴△ABC≌△DEF，∴∠ACB＝∠DFE，∴BC∥EF．6. 两块完全相同的三角形纸板ABC和DEF，按如图所示的方式叠放，阴影部分为重叠部分，点O为边AC和DF 的交点.不重叠的两部分△AOF与△DOC是否全等？为什么？解：全等 .理由如下：∵两三角形纸板完全相同，∴BC=BF，AB=BD，∠A=∠D，∴AB－BF=BD－BC，即AF=DC.在△AOF和△DOC中，∵AF=DC，∠A=∠D，∠AOF=∠DOC，∴△AOF≌△DOC.7. 已知：如图，E,F在AC上，AD∥CB且AD=CB，∠D ＝∠B.求证：AE=CF.2∵AD∥CB∴∠A=∠C又∵AD=CB，∠D=∠B∴△ADF≌△CBE∴AF=CE∴AF+EF=CE+EF即AE=CF8. 在△ABC中,AB=CB,∠ABC=90o,F为AB延长线上一点,点E在BC上,且AE=CF.求证:Rt△ABE≌Rt△CBF;若∠CAE=30o,求∠ACF度数.CF 第22题图∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt△ABE和Rt△CBF中,∵AE=CF, AB=BC, ∴Rt△ABE≌Rt△CBF∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠ACB=45°.∵∠BAE=∠CAB-∠CAE=45°-30°=15°.由知Rt△ABE≌Rt△CBF，∴∠BCF=∠BAE=15°, ∴∠ACF=∠BCF+∠ACB=45°+15°=60°.9. 如图6,AB?BD于点B,ED?BD于点D,AE交BD于点C,且BC?DC.求证AB?ED.D图E?证明:∵AB?BD,ED?BD ∴?ABC??D?90在?ABC和?EDC中??ABC??D??BC?DCACB??ECD3∴?ABC≌?EDC∴AB?ED10．如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连结BE、EC．试猜想线段BE和EC的数量及位置关系，并证明你的猜想．EACBE=EC，BE⊥EC∵AC=2AB，点D是AC的中点∴AB=AD=CD∵∠EAD=∠EDA=45°∴∠EAB=∠EDC=135°∵EA=ED∴△EAB≌△EDC∴∠AEB=∠DEC，EB=EC∴∠BEC=∠AED=90°∴BE=EC，BE⊥EC11. 已知：如图，E,F在AC上，AD∥CB且AD=CB，∠D ＝∠B.求证：AE=CF.∵AD∥CB∴∠A=∠C又∵AD=CB，∠D=∠B∴△ADF≌△CBE∴AF=CE∴AF+EF=CE+EF即AE=CF12. 如图，D，E，分别是 AB，AC 上的点，且AB=AC，AD=AE．求证∠B=∠C．证明：在△ABE和△ACD中，AB＝AC ∠A＝∠A AE＝AD∴△ABE≌△ACD∴∠B=∠C13. 如图，在△ABC中，AD是中线，分别过点B、C作AD及其延长线的垂线BE、CF，垂足分别为点E、F．求证：BE=CF．∵在△ABC中，AD是中线，∴BD=CD，∵CF⊥AD，BE⊥AD，∴∠CFD＝∠BED＝90° ，在△BED与△CFD中，∵∠BED＝∠CFD，∠BDE＝∠CDF，BD＝CD，∴△BED≌△CFD，∴BE=CF．14. 已知:如图,在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.求证:AB=AC证明∵AD平分∠EDC,∴∠ADE=∠ADC,又DE=DC,AD=AD, ∴△ADE≌△ADC, ∴∠E=∠C,又∠E=∠B, ∴∠B =∠C, ∴AB=AC.15. 如图，在平行四边形ABCD 中，E为BC 中点，AE 的延长线与DC的延长线相交于点F.证明：∠DFA = ∠FAB；证明: △ABE≌△FCE.证明：∵AB与CD是平行四边形ABCD的对边，∴AB∥CD，∴∠F=∠FAB．在△ABE和△FCE中，∠FAB=∠F ∵ ∠AEB=∠FEC BE=CE ∴ △ABE≌△FCE．16．如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．求证：△ACD≌△BCE；若∠D=50°，求∠B的度数．5全等到三角形练习题及答案1、下列判定直角三角形全等的方法，不正确的是A、两条直角边对应相等。