2.3平行的性质练习课

平行的判定与性质知识点一：直线与平面平行的判定及性质直线与平面平行的判断判定文字描述直线和平面在空间平面永无交点，则直线和平面平行（定义）平面外的一条直线一次平面内的一条直线平行，则该直线与此平面平行图形条件a与α无交点结论a∥αb∥α线线平行，则线面平行（线与面的平行问题一定要排除现在直线内的情况）直线与平面平行的性质性质文字描述一条直线与一个平面平行，则这条直线与该平面无交点一条直线和一个平面平行，则过这条直线的任一平面与此平面相交，这条直线和交线平行．图形条件a∥αa∥αa⊂βα∩β＝b结论a∩α＝∅a∥b线面平行，则线线平行例1正方形ABCD与正方形ABEF所在平面相交于AB，在AE、BD上各有一点P、Q，且AP＝DQ.求证：PQ∥平面BCE.证明：若一条直线与两个相交平面都平行，则这条直线平行于两个平面的交线．知识点二：平面与平面平行的判定及性质平面与平面平行的判定判定文字描述如果两个平面无公共点，责成这两个平面平行一个平面内有两条相交直线与另一个平面平行，那么这两个平面平行．如果两个平面同时垂直于一条直线，那么这两个平面垂直。

图形条件α∩β＝∅a，b⊂βa∩b＝Pa∥αb∥αl⊥αl⊥β结论α∥βα∥βα∥β平面与平面平行的性质性质文字描述如果两个平行平面同时和第三如果两个平面平行，那么其中一图形条件α∥β β∩γ＝b α∩γ＝aα∥β a ⊂β结论 a ∥b a ∥α例2 如图，在三棱柱ABC —A 1B 1C 1中，E ，F ，G ，H 分别是AB ，AC ，A 1B 1，A 1C 1的中点，求证：(1)B ，C ，H ，G 四点共面； (2)平面EFA1∥平面BCHG .如图，在正方体ABCD —A 1B 1C 1D 1中，O 为底面ABCD 的中心，P 是DD 1的中点，设Q 是CC 1上的点，问：当点Q 在什么位置时，平面D 1BQ ∥平面PAO?课堂练习：1．直线a ∥平面α，则a 平行于平面α内的( )D．无穷多条平行直线2．若直线a∥直线b，且a∥平面α，则b与α的位置关系是( )A．一定平行 B．不平行C．平行或相交 D．平行或在平面内3．下列说法正确的是( )A．若直线l平行于平面α内的无数条直线，则l∥αB．若直线l在平面α外，则l∥αC．若直线a∥b，b⊂平面α，则a∥αD．若直线a∥b，b⊂平面α，那么a平行于平面α内的无数条直线4．b是平面α外的一条直线，可以推出b∥α的条件是( )A．b与α内的一条直线不相交B．b与α内的两条直线不相交C．b与α内的无数条直线不相交D．b与α内的任何一条直线都不相交能力提升5．如果三个平面将空间分成6个互不重叠的部分，则这三个平面的位置关系是( )A．两两相交于三条交线B．两个平面互相平行，另一平面与它们相交C．两两相交于同一条直线D．B中情况或C中情况都可能发生6．[2011·威海质检] 已知直线l、m，平面α，且m⊂α，则“l∥m”是“l∥α”的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件7．[2011·泰安模拟] 设m，n表示不同直线，α，β表示不同平面，则下列结论中正确的是( )A．若m∥α，m∥n，则n∥αB．若m⊂α，n⊂β，m∥β，n∥α，则α∥βC．若α∥β，m∥α，m∥n，则n∥βD．若α∥β，m∥α，n∥m，n⊄β，则n∥β8．已知平面α∥平面β，P是α、β外一点，过点P的直线m与α、β分别交于点A、C，过点P的直线n与α、β分别交于点B、D，且PA＝6，AC＝9，PD＝8，则BD的长为( )9．[2010·福建卷] 如图K39－1，若Ω是长方体ABCD－A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1，则下列结论中不正确的是( ) A．EH∥FGB．四边形EFGH是矩形C．Ω是棱柱D．Ω是棱台10(10分)如图K39－3，已知P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点．求证：MN∥平面PAD；图K39－3 11(13分)[2011·九江七校联考] 如图K39－4所示，四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD＝AB＝2，E，F，G分别为PC、PD、BC的中点．求证：PA∥平面EFG；图K39－4课后练习：1、下列命题中正确的是（）（A）平行于同一个平面的两条直线平行（B）垂直于同一条直线的两条直线平行（C）若直线a与平面α内的无数条直线平行，则a∥α（D）若一条直线平行两个平面的交线，则这条直线至少平行两个平面中的一个2．平面α∩平面β＝a，平面β∩平面γ＝b，平面γ∩平面α＝c，若a∥b，则c与a，b的位置关系是（A）c与a，b都异面（B）c与a，b都相交（C）c至少与a，b中的一条相交（D）c与a，b都平行3．在正方体ABCD－A1B1C1D1中，与平面AB1C平行的直线是（）（A）DD1（B）A1D1（C）C1D1（D）A1D4．下列四个命题：（1）存在与两条异面直线都平行的平面；（2）过空间一点，一定能作一个平面与两条异面直线都平行；（3）过平面外一点可作无数条直线与平面平行；（4）过直线外一点可作无数个平面与直线平行；其中正确的命题是（）（A）（1），（3）（B）（2），（4）（C）（1），（3），（4）（D）（2），（3），（4）5．若直线a与平面α内的无数条直线平行，则a与α的关系为。

《平移与平行》同步练习一、判断题1.不相交的两条直线一定是平行线。

（）2.经过直线外一点画这条直线的平行线可以画无数条。

（）3.一个三角形的三条边不可能是相互平行的。

（）4.平行四边形的四条边是两组平行线。

（）5.同一平面内的两条直线不相交就平行。

（）二、单选题1.两条相交直线，若将他们平移，则移动后的直线与原直线构成的图形可能是（）。

A. 三角形B. 梯形C. 平行四边形D. 五边形2.梯形有（）组平行线。

A. 0B. 1C. 23.图形经过（)后，与原图形相等。

A. 平移B. 平行C. 旋转4红旗沿着旗杆上升的运动是（）。

A. 旋转B. 平行C. 平移5.下列现象中，不属于平移的是（）。

A. 乘坐直升电梯从一楼到三楼。

B. 钟表的指针嘀嗒嘀嗒的走。

C. 火车在笔直的轨道上行驶。

三、填空题1.在同一平面内，________的两条直线，叫平行线。

2.双杠的两根杠是互相________的，铅笔平移前后的线条是________的。

3.过直线外一点，能画________条这条直线的平行线。

4.一个长方形有________组互相平行的对边。

5.正方形的两组对边互相________。

6.平行线间的距离处处________。

7.对于平行线，一定要在________范畴内研究。

8.黑板上的上下两边是一组________。

9.平行四边形中，相对的两条边是互相________的。

10.平移后的图形与原图形________。

四、作图题1.过A点画已知直线的平行线。

2.过O点画直线AB的平行线。

3.过点P分别作出直线A和直线B的平行线。

五、解答题1.下图中有哪些线段是平行的，请写出三组。

2.下面哪组是平行线。

答案解析部分一、判断题1.【答案】错误【解析】【解答】不相交的两条直线不一定是平行线。

【分析】平行线必须是在同一平面内。

本题考查垂直与平行的特征及性质。

2.【答案】错误【解析】【解答】经过直线外一点画这条直线的平行线不可以画无数条。

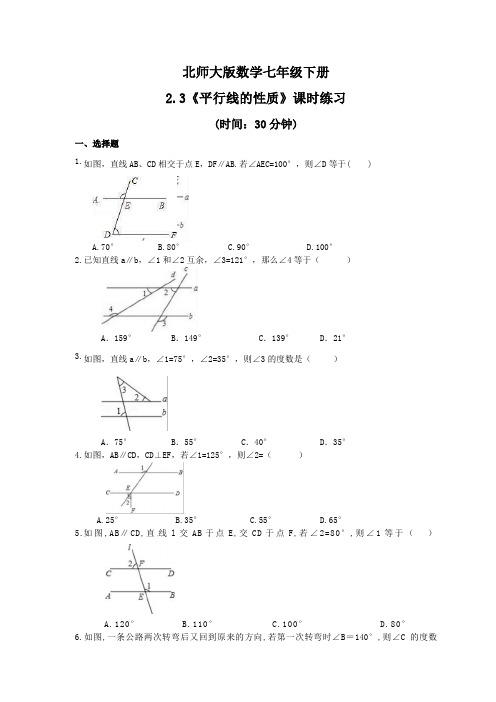
北师大版数学七年级下册2.3《平行线的性质》课时练习(时间：30分钟)一、选择题1.如图，直线AB、CD相交于点E，DF∥AB.若∠AEC=100°，则∠D等于( )A.70°B.80°C.90°D.100°2.已知直线a∥b，∠1和∠2互余，∠3=121°，那么∠4等于（）A．159° B．149° C．139° D．21°3.如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（）A．75° B．55° C．40° D．35°4.如图，AB∥CD，CD⊥EF，若∠1=125°，则∠2=（）A.25°B.35°C.55°D.65°5.如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=80°,则∠1等于（）A.120°B.110°C.100°D.80°6.如图,一条公路两次转弯后又回到原来的方向,若第一次转弯时∠B＝140°,则∠C的度数( )A.140°B.40°C.100°D.180°7.如图,直线m∥n,点A在直线m上,点B,C在直线n上,AB=BC,∠1=70°,CD⊥AB于D,那么∠2等于（）A.20°B.30°C.32°D.25°8.如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,则图中与∠AGE相等的角（）A.2个B.3个C.4个D.5个9.如图,已知a∥b,三角形直角顶点在直线a上,已知∠1=25°18/27//，则∠2度数是（）A.25°18/27//B.640 41/33//C.74°4133//D.64°41/43//10.如图所示，把一根铁丝折成图示形状后，AB∥DE，则∠BCD等于（）A.∠D+∠BB.∠B﹣∠DC.180°+∠D﹣∠BD.180°+∠B﹣∠D二、填空题11.如图,直线a∥b,∠1=85°,∠2=35°,则∠3为．12.如图，AB∥CD，将矩形EFGH的顶点E和F分别放在直线AB与CD上，若∠1=40°，则∠CFG的度数等于．13.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG= ．14.如图，AB∥CD，∠ɑ=三、解答题15.如图，AB∥CD，若∠ABE=120°，∠DCE=35°，求∠BEC的度数．16.如图,已知D是BC上的一点,DE∥AC,DF∥AB．求证:∠A＋∠B＋∠C=180°．17.如图, ∠BAP+∠APD=180°，AE//FP.求证：∠1=∠2.18.如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF，下面给出证法1. 请阅读证法1后，找出与证法1不同的证法2，并写出证明过程.证法1：设∠1、∠2、∠3的度数分别为x,2x,3x.∵AB∥CD，∴2x+3x=180°，解得x=36°∴∠1=36°，∠2=72°，∠3=108°∵∠EBD=180°，∴∠EBA=72°∴BA平分∠EBF北师大版数学七年级下册2.3《平行线的性质》课时练习（含答案）参考答案一、选择题1.B.2.B3.C4.B5.答案为：D；6.答案为：C；二、填空题7.答案为：50°8.答案为：130°．9.答案为：68°10.答案为：85°三、解答题11.解：如图，延长BE交CD的延长线于点F，∵AB∥CD[已知]∴∠ABE+∠EFC=180°[两直线平行，同旁内角互补]又∵∠ABE=120°，[已知]∴∠EFC=180°﹣∠B=180°﹣120°=60°，[两直线平行，同旁内角互补]∵∠DCE=35°∴∠BEC=∠DCE+∠EFC=35°+60°=95°12.【证明】∵ DE∥AC（已知），∴∠BED＝∠A，∠BDE＝∠C（两直线平行，同位角相等）．∵ DF∥AB（已知），∴∠BED＝∠EDF（两直线平行，内错角相等），∠FDC＝∠B（两直线平行，同位角相等）．∴∠EDF＝∠A（等量代换）．∵∠BDE＋∠EDF＋∠FDC＝180°（平角定义），∴∠C＋∠A＋∠B＝180°（等量代换）．即∠A＋∠B＋∠C＝180°．13.解：∵∠BAP+∠APD=180．∴AB//CD∴∠BAP=∠APC∵AE//FP∴∠EAP=∠APF∴∠BAP-∠EAP=∠APC-∠APF即∠l=∠2．14.条件①∠EBC=∠FCB，或CF∥BE,证明略。

2.2.3直线与平面平行的性质一、基础过关1．若平面α∥平面β，直线a∥α，点B∈β，则在β内过点B的所有直线中()A．不一定存在与a平行的直线B．只有两条与a平行的直线C．存在无数条与a平行的直线D．存在唯一一条与a平行的直线答案 A解析当a⊂β，B∈a时，过点B不存在与a平行的直线．2.如图所示，长方体ABCD－A1B1C1D1中，E、F分别是棱AA1和BB1的中点，过EF的平面EFGH分别交BC和AD于G、H，则HG与AB的位置关系是()A．平行B．相交C．异面D．平行和异面答案 A解析∵E、F分别是AA1、BB1的中点，∴EF∥AB.又AB⊄平面EFGH，EF⊂平面EFGH，∴AB∥平面EFGH.又AB⊂平面ABCD，平面ABCD∩平面EFGH＝GH，∴AB∥GH.3．若一条直线和一个平面平行，夹在直线和平面间的两条线段相等，那么这两条线段所在直线的位置关系是()A．平行B．相交C．异面D．平行、相交或异面答案 D解析画图可知两直线可平行、相交或异面，故选D.4．过平面α外的直线l，作一组平面与α相交，如果所得的交线为a，b，c，…，则这些交线的位置关系为()A ．都平行B ．都相交且一定交于同一点C ．都相交但不一定交于同一点D ．都平行或都交于同一点答案 D解析 分l ∥α和l 与α相交两种情况作答，对应的结果是都平行和都交于同一点．5．如图，正方体ABCD —A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上．若EF ∥平面AB 1C ，则线段EF 的长度等于______．答案 2 解析 由于在正方体ABCD —A 1B 1C 1D 1中，AB ＝2，∴AC ＝2 2.又E 为AD 的中点，EF ∥平面AB 1C ，EF ⊂平面ADC ，平面ADC ∩平面AB 1C ＝AC ，∴EF ∥AC ，∴F 为DC 的中点，∴EF ＝12AC ＝ 2.6.如图所示，ABCD —A 1B 1C 1D 1是棱长为a 的正方体，M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点，P 是上底面的棱AD 上的一点，AP ＝a3，过P ，M ，N 的平面交上底面于PQ ，Q 在CD 上，则PQ ＝________.答案 223a解析 ∵MN ∥平面AC ，平面PMN ∩平面AC ＝PQ ，∴MN ∥PQ ，易知DP ＝DQ ＝2a3，故PQ ＝PD 2＋DQ 2＝2DP ＝22a3.7．如图所示，四面体A －BCD 被一平面所截，截面EFGH 是一个矩形．(1)求证：CD ∥平面EFGH ；(2)求异面直线AB 、CD 所成的角．(1)证明 ∵截面EFGH 是矩形，∴EF ∥GH .又GH ⊂平面BCD ，EF ⊄平面BCD .∴EF∥平面BCD.而EF⊂平面ACD，平面ACD∩平面BCD＝CD，∴EF∥CD.又EF⊂平面EFGH，CD⊄平面EFGH，∴CD∥平面EFGH.(2)解由(1)知CD∥EF，同理AB∥FG，由异面直线所成角的定义知，∠EFG即为所求．故AB、CD所成的角为90°.二、能力提升8．若直线a∥平面α，a∥平面β，α∩β＝直线b，则()A．a∥b或a与b异面B．a∥bC．a与b异面D．a与b相交答案 B解析a∥b.理由如下：如图，过a作平面γ交平面α于c，因为a∥α，所以a∥c.过a作平面ε交平面β于d，因为a∥β，所以a∥d.所以c∥d.又c⊄β，d⊂β，所以c∥β又c⊂α，a∩β＝b，所以c∥b，所以a∥b.9.如图，四棱锥S－ABCD的所有的棱长都等于2，E是SA的中点，过C，D，E三点的平面与SB交于点F，则四边形DEFC的周长为()A．2＋ 3 B．3＋ 3C．3＋2 3 D．2＋2 3答案 C解析因为AB＝BC＝CD＝AD＝2，所以四边形ABCD为菱形，所以CD∥AB.又CD⊄平面SAB，AB⊂平面SAB，所以CD∥平面SAB.又CD⊂平面CDEF，平面CDEF∩平面SAB＝EF，所以CD∥EF.所以EF∥AB.又因为E 为SA 的中点，所以EF ＝12AB ＝1. 又因为△SAD 和△SBC 都是等边三角形，所以DE ＝CF ＝2×sin60°＝3，所以四边形DEFC 的周长为CD ＋DE ＋EF ＋FC ＝2＋3＋1＋3＝3＋2 3.10.如图所示，在空间四边形ABCD 中，E 、F 、G 、H 分别是四边上的点，它们共面，并且AC ∥平面EFGH ，BD ∥平面EFGH ，AC ＝m ，BD ＝n ，当四边形EFGH 是菱形时，AE ∶EB ＝________.答案 m ∶n解析 ∵AC ∥平面EFGH ，∴EF ∥AC ，GH ∥AC ，∴EF ＝HG ＝m ·BE BA， 同理EH ＝FG ＝n ·AE AB. ∵EFGH 是菱形，∴m ·BE BA ＝n ·AE AB， ∴AE ∶EB ＝m ∶n .11.ABCD 是平行四边形，点P 是平面ABCD 外一点，M 是PC 的中点，在DM 上取一点G ，过G 和AP 作平面交平面BDM 于GH ，求证：AP ∥GH . 证明 如图所示，连接AC 交BD 于O ，连接MO ，∵ABCD 是平行四边形，∴O 是AC 中点，又M 是PC 的中点，∴AP ∥OM .根据直线和平面平行的判定定理，则有P A ∥平面BMD .∵平面P AHG ∩平面BMD ＝GH ，根据直线和平面平行的性质定理，则有AP ∥GH .12.如图所示，P 为平行四边形ABCD 所在平面外一点，M 、N 分别为AB 、PC 的中点，平面P AD ∩平面PBC ＝l .(1)求证：BC ∥l ；(2)MN 与平面P AD 是否平行？试证明你的结论．(1)证明 因为BC ∥AD ，AD ⊂平面P AD ，BC ⊄平面P AD ，所以BC ∥平面P AD .又平面P AD ∩平面PBC ＝l ，BC ⊂平面PBC ，所以BC ∥l .(2)解 MN ∥平面P AD .证明如下：如图所示，取PD 中点E .连接EN 、AE .又∵N 为PC 中点，∴EN 綊12AB ∴EN 綊AM ，∴四边形ENMA 为平行四边形，∴AE ∥MN .又∵AE ⊂平面P AD ，MN ⊄平面P AD ，∴MN ∥平面P AD .三、探究与拓展13.如图，几何体E －ABCD 是四棱锥，△ABD 为正三角形，CB ＝CD ，EC ⊥BD .(1)求证：BE ＝DE ；(2)若∠BCD ＝120°，M 为线段AE 的中点，求证：DM ∥平面BEC . 证明 (1)如图，取BD 的中点O ，连接CO ，EO .由于CB ＝CD ，所以CO ⊥BD .又EC ⊥BD ，EC ∩CO ＝C ，CO ，EC ⊂平面EOC ，所以BD ⊥平面EOC ，因此BD ⊥EO .又O 为BD 的中点，所以BE ＝DE .(2)解 如图，延长AD ，BC 交于点F ，连接EF .因为CB ＝CD ，∠BCD ＝120°，所以∠CBD ＝30°.因为△ABD 为正三角形，所以∠BAD ＝60°，∠ABC ＝90°，因为∠AFB ＝30°，所以AB ＝12AF . 又AB ＝AD ，所以D 为线段AF 的中点． 连接DM ，由于点M 是线段AE 的中点， 因此DM ∥EF .又DM ⊄平面BEC ，EF ⊂平面BEC ， 所以DM ∥平面BEC .。

课后导练基础达标1在以下四个命题中，真命题是（）①在一个平面内有两点到另一个平面的距离相等都是d(d＞0)，则这两个平面平行②在一个平面内有三点到另一个平面的距离都是d(d＞0)，则这两个平面平行③在一个平面内有无数个点到另一个平面的距离都是d(d＞0)，则这两个平面平行④一个平面内任意一点到另一个平面的距离都是d(d＞0)，则这两个平面平行A.②③④B.④C.②③D.②④解析：命题①中的两点无论在另一个平面的同侧还是异侧，这两个平面均有可能相交.所以①是错误的；同理可知②③均错.只有④正确.答案：B2平面α上有不共线的三点到平面β的距离相等，则α与β的关系是（）A．平行B．相交C．垂直D．不确定解析：若三点在β的同侧，则α∥β,否则相交，应选D.答案：D3设a、b是两条互不垂直的异面直线，过a、b分别作平面α、β．对于下面四种情况可能的情况有（）①b∥α ②b⊥α ③a∥β ④α与β相交A．1种B．2种C．3种D．4种解析：对于②来说，若b⊥α,又∵a⊂α,∴b⊥a与a，b不垂直矛盾，∴②错.答案：C4已知平面α∥β，直线a∥α，点B∈β，则在β内过B的所有直线中（）A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一的直线与a平行解析：若a⊂β,且B∈a,此时，不存在.若B∉a,此时存在唯一直线与a平行.答案：A5已知α∩β=c,a∥α,a∥β，则a与c的位置关系是_______________解析：a∥α,a∥β,α∩β=c,则a∥c(前面已证).答案：平行6直线a∥b,a∥平面α,则b与平面α的位置关系是_______________解析：当直线b在平面α外时，b∥α;当直线b在平面α内时，b⊂α.答案：b∥α或b∩α7a∥α,A是α的另一侧的点，B、C、D∈α,线段AB、AC、AD交α于E、F、G，若BD=4，CF=4，AF=5，则EG=__________.（如图）解析：∵a ∥α,EG=α∩平面ABD ，∴a ∥EG,即BD ∥EG.∴FCAF AF BD EG CD BC FG EF AC AF CD FG BC EF +==++=== 则EG=9204545=+⨯=+•FC AF BD AF . 答案：920 8已知:α∩β=l,a ⊂α,b ⊂β,a ∥b ， 求证：a ∥b ∥l.证明：∵a ∥b,b ⊂β,a ⊄β,由线面平行的判定定理知a ∥β.又知a ⊂α,α∩β=l,由线面平行的性质知,a ∥l,∴a ∥b ∥l.综合应用9如右图，四边形ABCD 是矩形，P 平面ABCD ，过BC 作平面BCFE 交AP 于E ，交DP 于点F.求证：四边形BCFE 是梯形.证明：在矩形ABCD 中，BC ∥AD,又∵BC ⊄面PAD ，AD ⊂面PAD ，∴BC ∥面PAD.又面BC ⊂面BCFE ，且面BCFE∩面PAD=EF,∴EF ∥BC,又BC AD,EF≠AD,∴EF≠BC,故四边形BCFE 为梯形.10已知:AB 、CD 为异面线段，E 、F 分别为AC 、BD 的中点，过E 、F 作平面α∥AB. 求证：CD ∥α.证明：如图，连结AD 交面α于点H ，连结EH ，FH,∵AB ∥α,AB ⊂面ABD ，且面ABD∩α=FH,∴AB ∥HF.又∵F 为BD 中点,∴H 为AD 中点，又E 为AC 中点，∴EH ∥CD,又∵EH ⊂面α,CD ⊄面α，故CD ∥α.11如图,P 为平行四边形ABCD 所在平面外一点，M 、N 分别是AB 、PC 的中点,平面PAD∩平面PBC ＝l.(1)求证:BC ∥l;(2)MN 与平面PAD 是否平行?试证明你的结论.证明：（1）在ABCD 中，BC ∥AD,BC ⊄面PAD ，AD ⊂面PAD ，∴BC ∥面PAD.又面PAD∩面PBC=l,且BC ⊂面PBC ，故BC ∥l.（2）MN ∥平面PAD.证明如下，取PD 中点E ，连AE ，NE ；∵N 是PC 中点，∴NE21CD, 又M 为AB 的中点，∴AM 21DC, ∴AM NE,∴AE ∥MN.又∵AE ⊂面PAD ，MN ⊄面PAD,∴MN ∥面PAD.拓展探究12如图，已知空间四边形ABCD ，作一截面EFGH ，且E 、F 、G 、H 分别在BD 、BC 、AC 、AD 上.(1)若平面EFGH 与AB 、CD 都平行，求证：EFGH 是平行四边形；(2)若平面EFGH 与AB 、CD 都平行，且CD ⊥AB ，求证：EFGH 是矩形；(3)若EFGH 与AB 、CD 都平行，且CD ⊥AB ，CD=a,AB=b,问点E 在什么位置时，EFGH 的面积最大？(1)证明：∵AB ∥面EFGH,AB ⊂面ABD ，面ABD∩面EFGH=EH ，∴AB ∥EH.同理可证AB ∥GF ，∴GF ∥EH.又∵CD ∥面EFGH ，同理可证EF ∥GH.故四边形EFGH 是平行四边形.（2）证明：由（1）知，AB ∥EH,CD ∥EF,又∵CD ⊥AB,∴EF ⊥EH,故EFGH 为矩形.（3）解：设BE=x,由上知BD BE CD EF BD DE AB EH ==,,∴BDx BD AB BD DE -=•·b, EF=BDx ·a. ∴S 矩形EFGH =EF·EH=BD ab x(BD-x)=BDab (-x 2+BDx) =BD ab［-（x-2BD)2+42BD ）］，∴x=2BD即E 为BD 中点时，面积最大.。