立体图形的认识和计算

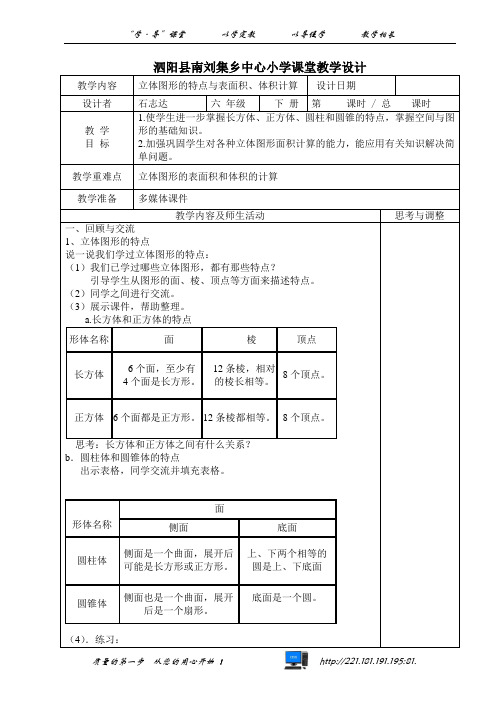
泗阳县南刘集乡中心小学课堂教学设计教学内容立体图形的特点与表面积、体积计算设计日期设计者 石志达 六 年级 下 册 第 课时 / 总 课时教 学 目 标 1.使学生进一步掌握长方体、正方体、圆柱和圆锥的特点，掌握空间与图形的基础知识。

2.加强巩固学生对各种立体图形面积计算的能力，能应用有关知识解决简单问题。

教学重难点 立体图形的表面积和体积的计算 教学准备多媒体课件教学内容及师生活动思考与调整一、回顾与交流 1、立体图形的特点说一说我们学过立体图形的特点：（1）我们已学过哪些立体图形，都有那些特点？引导学生从图形的面、棱、顶点等方面来描述特点。

（2）同学之间进行交流。

（3）展示课件，帮助整理。

a.长方体和正方体的特点 形体名称面棱顶点长方体6个面，至少有 4个面是长方形。

12条棱，相对的棱长相等。

8个顶点。

正方体 6个面都是正方形。

12条棱都相等。

8个顶点。

思考：长方体和正方体之间有什么关系？ b ．圆柱体和圆锥体的特点出示表格，同学交流并填充表格。

（4）．练习：形体名称面侧面底面 圆柱体侧面是一个曲面，展开后 可能是长方形或正方形。

上、下两个相等的 圆是上、下底面 圆锥体侧面也是一个曲面，展开后是一个扇形。

底面是一个圆。

长方体和正方体都有（ ）个面，有（ ）条棱，有（ ）个顶点。

长方体（ ）面的面积相等；相对的（ ）条棱长相等；正方体的每个面都是（ ）形，每个面的面积都（ ）。

把圆柱的侧面沿高展开，一般可以得到 （ ），这个图形的长相当于（ ），宽相当于（ ）。

2、立体图形的表面积和体积的计算（1） 小组交流：如何计算长方体、正方体、圆柱体表面积和体积？ 如何计算圆锥的体积？圆锥的体积公式是怎样推导得来的？ （2）汇报交流结果。

a. 长方形的表面积=2 ×长×宽+2 ×长×高+2 ×宽×高S=2ab+2ah+2bhb. 正方体的表面积=每个面的面积×6S=6×a ×ac. 圆柱的表面积= 侧面积+底面积×2 圆柱的侧面积=底面周长×高d.长方体的体积=长×宽×高 v=a ×b ×h 正方体的体积=棱长×棱长×棱长 V= a ×a ×a 圆柱体的体积=底面积×高 v=s ×h圆锥体的体积=底面积×高×31 v=s ×h ×31（3）思考：长方体和正方体侧面展开图是什么形状？侧面积怎样计算？一、 巩固练习1、计算下列立体图形的表面积和侧面积2. 一个长方体的无盖铁盒，长是4dm ，宽3dm ，高2.5dm ，制作这个铁盒至少需要铁皮多少平方分米？3. 一个圆柱形的水池，直径是20米，深2米 ①这个水池占地多少平方米？②在池的侧面和池底贴磁砖，磁砖的面积是多少？ 三、课堂小结1、说一说长方体、正方体、圆柱和圆锥的特点。

总结立体图形的知识点一、立体图形的定义立体图形是指有三个维度的图形，它具有长度、宽度和高度。

在数学中，我们所说的立体图形通常是指三维几何图形，它们存在于空间中，具有一定的体积和表面积。

而与之相对应的是平面图形，它只具有长度和宽度，无法展现出立体图形那种立体感。

二、常见的立体图形1. 正方体：正方体是一种每个面都是正方形的立体图形。

它具有六个面、十二条边和八个顶点。

2. 长方体：长方体是一种每个面都是矩形的立体图形。

它也具有六个面、十二条边和八个顶点。

3. 圆柱体：圆柱体由两个平行的并且相等的圆面以及一个侧面围成。

它的侧面是一个矩形，其长度等于两个圆面的周长，宽度等于两个圆面之间的距离。

4. 圆锥体：圆锥体由一个圆锥面和一个圆锥侧面构成。

它的侧面是一个扇形，其面积等于圆锥底面积与母线的乘积除以2。

5. 球体：球体是由无数个半径相等的点构成的图形。

它的表面是完全封闭的，不像其他立体图形有明显的边界。

球体的表面积和体积的计算比较特殊，需要使用一些特殊的公式来得到。

三、计算立体图形的表面积和体积1. 表面积：对于常见的立体图形，我们可以通过公式来计算其表面积。

例如，正方体的表面积就等于六个面积之和，而长方体的表面积也可以用公式2lw + 2lh + 2wh进行计算。

其他立体图形的表面积计算也可以通过相应的公式来完成。

2. 体积：立体图形的体积是指其所围成的空间的大小。

计算立体图形的体积也需要使用相应的公式。

例如，正方体的体积就等于边长的立方，而长方体的体积可以用公式lwh来计算。

其他立体图形的体积计算同样也可以通过相应的公式来完成。

四、立体图形的性质1. 对称性：许多立体图形具有一定的对称性。

例如，正方体在某些对角线上是对称的，长方体也在某些对角线上是对称的。

这种对称性在几何学中是一个重要的性质。

2. 体积与形状的关系：在相同的表面积条件下，立体图形的体积越大，其形状就越扁。

这是由于形状的扁平程度与立体图形的体积具有一定的关系。

《一年级数学立体图形知识点总结》在一年级的数学学习中，立体图形是一个重要的知识点。

认识立体图形不仅能够帮助孩子们建立空间观念，还能为他们后续的数学学习打下坚实的基础。

一、立体图形的种类1. 长方体长方体是一种常见的立体图形，它有六个面，每个面都是长方形。

长方体的相对面完全相同，相对的棱长度相等。

例如，我们日常生活中的书本、文具盒等物品的形状就接近长方体。

2. 正方体正方体是一种特殊的长方体，它的六个面都是完全相同的正方形。

正方体的十二条棱长度都相等。

像魔方、骰子等就是正方体。

3. 圆柱圆柱有两个底面和一个侧面。

底面是圆形，侧面是一个曲面。

圆柱的两个底面完全相同且平行。

在生活中，我们常见的易拉罐、柱子等物体的形状就是圆柱。

4. 球球是一个曲面图形，没有平面。

球可以向任意方向滚动。

比如，我们玩的篮球、足球等都是球。

二、立体图形的特征1. 面的特征（1）长方体和正方体都有六个面。

长方体的面可以是长方形，也可能有两个相对的面是正方形。

正方体的六个面都是正方形。

（2）圆柱有两个底面和一个侧面。

底面是圆形，侧面是曲面。

（3）球没有平面，只有一个曲面。

2. 棱的特征（1）长方体有十二条棱，相对的棱长度相等。

（2）正方体的十二条棱长度都相等。

（3）圆柱没有棱。

（4）球没有棱。

3. 顶点的特征（1）长方体有八个顶点。

（2）正方体也有八个顶点。

（3）圆柱没有顶点。

（4）球没有顶点。

三、立体图形的观察与比较1. 观察立体图形让孩子们通过观察实物或模型，了解不同立体图形的形状、大小、颜色等特征。

可以引导孩子们从不同的角度观察立体图形，如从正面、侧面、上面观察，培养他们的空间观察能力。

2. 比较立体图形（1）比较形状：让孩子们比较不同立体图形的形状，说出它们的相同点和不同点。

例如，长方体和正方体都有六个面，但正方体的六个面都是正方形，而长方体的面可能是长方形。

（2）比较大小：可以通过比较立体图形的体积或表面积来比较它们的大小。

小学数学立体图形知识汇总（一）长方体1、特征六个面都是长方形（有时有两个相对的面是正方形）。

相对的面面积相等，12条棱相对的4条棱长度相等。

有8个顶点。

相交于一个顶点的三条棱的长度分别叫做长、宽、高。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

把长方体放在桌面上，最多只能看到三个面。

长方体或者正方体6个面的总面积，叫做它的表面积。

2、计算公式s=2(ab+ah+bh)V=shV=abh（二）正方体1、特征六个面都是正方形六个面的面积相等12条棱，棱长都相等有8个顶点正方体可以看作特殊的长方体S表=6a²v=a3（三）圆柱1、圆柱的认识圆柱的上下两个面叫做底面。

圆柱有一个曲面叫做侧面。

圆柱两个底面之间的距离叫做高。

进一法：实际中，使用的材料都要比计算的结果多一些，因此，要保留数的时候，省略的位上的是4或者比4小，都要向前一位进1。

这种取近似值的方法叫做进一法。

2、计算公式s侧=chs表=s侧+s底×2v=sh/3（四）圆锥1、圆锥的认识圆锥的底面是个圆，圆锥的侧面是个曲面。

从圆锥的顶点到底面圆心的距离是圆锥的高。

测量圆锥的高：先把圆锥的底面放平，用一块平板水平地放在圆锥的顶点上面，竖直地量出平板和底面之间的距离。

把圆锥的侧面展开得到一个扇形。

v=sh/3（五）球1、认识球的表面是一个曲面，这个曲面叫做球面。

球和圆类似，也有一个球心，用O表示。

从球心到球面上任意一点的线段叫做球的半径，用r表示，每条半径都相等。

通过球心并且两端都在球面上的线段，叫做球的直径，用d表示,每条直径都相等,直径的长度等于半径的2倍，即d=2r。

2、计算公式d=2r。