下载文档原格式
计算机图形学课程设计一、课程目标知识目标：1. 让学生掌握计算机图形学的基本概念、基本原理和基本算法，如二维图形的表示、变换、裁剪和三维图形的建模、光照模型等。
2. 使学生了解计算机图形学在实际应用中的发展现状和前景，如虚拟现实、计算机辅助设计等。
3. 帮助学生建立计算机图形学与相关学科（如数学、物理、艺术等）的联系，提高跨学科素养。
技能目标：1. 培养学生运用计算机图形学知识解决实际问题的能力，如使用相关软件进行二维绘图、三维建模等。
2. 提高学生的编程能力，使其能够使用至少一种计算机图形学编程库（如OpenGL、DirectX等）实现基本图形绘制和动画效果。
3. 培养学生的团队协作能力和沟通表达能力，通过小组项目实践，共同完成具有一定难度的计算机图形学任务。
情感态度价值观目标：1. 激发学生对计算机图形学的兴趣，培养其主动探究、创新实践的精神。
2. 培养学生具有良好的审美观，能够从美学的角度评价和优化计算机生成的图形。
3. 强化学生的版权意识，尊重他人知识产权，遵循学术道德，树立正确的价值观。
本课程针对高中年级学生，结合学科特点和教学要求，将目标分解为具体的学习成果，以便于后续的教学设计和评估。
通过本课程的学习，期望学生能够掌握计算机图形学的基础知识，提高实际操作技能，培养良好的情感态度价值观。
二、教学内容1. 计算机图形学基本概念与历史：介绍计算机图形学的定义、发展历程、应用领域及发展趋势。
- 教材章节：第一章 计算机图形学概述- 内容安排：1课时2. 二维图形的表示与处理：讲解二维图形的数学表示、几何变换、裁剪算法等。
- 教材章节：第二章 二维图形处理- 内容安排：4课时3. 三维图形的建模与渲染：介绍三维图形的建模方法、光照模型、纹理映射等。
- 教材章节：第三章 三维图形处理- 内容安排：5课时4. 计算机动画与视觉效果：探讨计算机动画原理、关键帧动画、粒子系统等视觉效果技术。
- 教材章节：第四章 计算机动画与视觉效果- 内容安排：4课时5. 计算机图形学编程实践：学习计算机图形学编程库（如OpenGL、DirectX 等）的基本使用，完成二维和三维图形绘制实例。
计算机图形学课程设计设计题目：画三次Bezier曲线和三次B样条曲线班级：姓名：学号：一、总体目标和要求1 课程设计目的本课程主要内容包括计算机图形学的研究内容、发展与应用，图形输入输出设备，图形显示原理，图形软件标准，基本图形生成算法，图形几何变换与裁剪，自由曲线和曲面，三维实体造型，分形几何造型，分形艺术，隐藏面消除，光照模型，颜色模型，光线跟踪，纹理细节模拟，常用的计算机动画技术和软件等。
通过本课程设计，使自己了解计算机图形学的有关原理、算法及系统，掌握基本图形显示程序设计方法，及二维和三维图形变换程序设计方法，为进一步学习计算机辅助设计方面的技术知识打下基础。
2 目标以图形学算法为目标，深入研究。
续而策划设计实现一个能够表现计算机图形学算法原理的或完整过程的演示系统，并能从某些方面做出评价和改进意见。
通过完成一个完整程序，经历策划、设计、开发、总结。
达到：（1）巩固和实践计算机图形学课程中的理论和算法；（2）学习表现计算机图形学算法的技巧；（3）培养认真学习积极探索的精神。
3总体要求策划、设计并实现一个能够充分表现图形学算法的系统，界面要求美观大方，能清楚地演示算法执行的每一个步骤。
二、内容与要求1设计题目画三次Bezier曲线和三次B样条曲线。
2设计要求利用计算机图形学原理画出三次Bezier曲线和三次B样条曲线。
三、算法描述（1）画三次Bezier曲线根据Q(t)=∑P i•B• C i n t i(1-t)n-i（∑中的n=3）并且 C i nBEZ 0,3BEZ 1,3(u)=3u(1-u)(1-u)BEZ2,3(u)=3uu(1-u)BEZ3,3(u)=3uuu三次Bezier函数可以写成P(u)=[u3 u2 u 1]×M×[a b c d] 其中M=[ -1 3 -3 1 ]3 -6 -3 0-3 3 0 01 0 0 0i=0（2）画三次B样条曲线Q i,3(t)=∑P i+l F l,3(t)= P i F0,3(t)+ P i+1 F1,3(t)+ P i+2 F2,3(t)+ P i+ 3 F3,3(t)（其中∑中的n=3）因为四个调和函数F0,3(t)、F1,3(t)、F2,3(t)和F3,3(t) 已知（参看公式7-5-3）因此只要给出四个控制点的位置矢量的坐标，当t在[0，1]范围内取离散地取100个点时（dt=0.01），分别求出每一个曲线上点，相邻点用直线段连接起来，就可以得到相应的B样条曲线。
宁夏师范学院数学与计算机科学学院《计算机图形学》实验报告实验序号：7 实验项目名称：二维图形变换菜单菜单项ID值图形变换（&T）缩放（&Z）ID_TRANSFORM_SCALE图形变换（&T）旋转（&R）ID_TRANSFORM_ROTATE图形变换（&T）对称（&S）ID_TRANSFORM_SYMMETRY 4、在CTransView视图类中添加消息映射函数；对象消息函数ID_TRANSFORM_SCALE COMMAND OnFigureCirleID_TRANSFORM_ROTATE COMMAND OnFigureEllipseID_TRANSFORM_SYMMETRY COMMAND OnTransformSymmetry5、添加自定义的成员变量：CPoint Pt[3]; //三角形定点数组float dAngle; //每一次旋转的角度在视图类CPP文件的构造函数中初始化成员变量Pt[0].x = 540; Pt[0].y = 220;Pt[1].x = 670; Pt[1].y = 130;Pt[2].x = 560; Pt[2].y = 120;dAngle = 0;6、在视图类的OnDraw()函数中加入下列代码，实现视图绘图。
void CTransView::OnDraw(CDC* pDC){CTransDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data here//绘出以以(540，220)、(670，130)、(560，120)为顶点的三角形。
pDC->MoveTo(Pt[0]);pDC->LineTo(Pt[1]);三、运行结果变换前：对称变换：缩放变换：旋转变换：五、教师评语成绩签名：日期：年月日。
计算机图形学图形变换实验五：图形变换⼀、实验⽬的：1、掌握图形变换的基本⽅法。
2、初步掌握映射菜单消息和捕获键盘消息的⽅法。
⼆、实验内容及要求：1、以三⾓形为例，使⽤Visual C＋＋实现⼆维图形的平移、旋转和缩放功能。
2、每⼈单独完成实验。
3、按要求撰写实验报告，写出实验⼼得，并在实验报告中附上程序的核⼼算法代码。
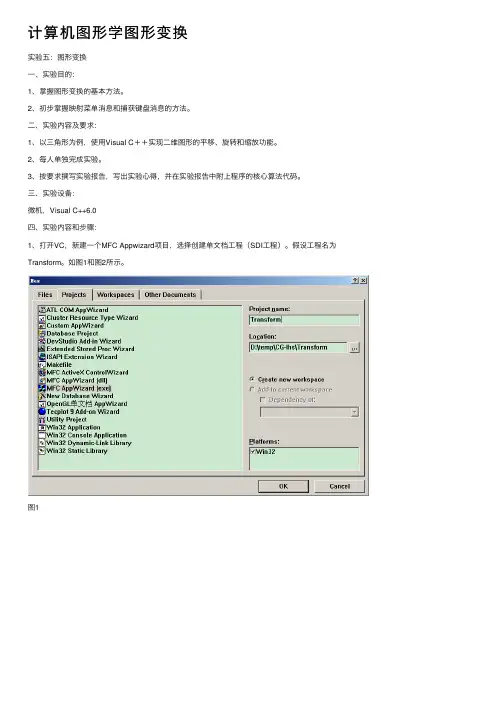
三、实验设备：微机，Visual C++6.0四、实验内容和步骤：1、打开VC，新建⼀个MFC Appwizard项⽬，选择创建单⽂档⼯程（SDI⼯程）。
假设⼯程名为Transform。
如图1和图2所⽰。
图1图22、在图2的界⾯上点击Finish，完成⼯程的创建。
3、在TransformView.h⽂件中，加⼊如下代码：public:CPoint Pt[3]; //存储三⾓形的三个顶点float dAngle; //存储三⾓形旋转的⾓度4、在类CTransformView的构造函数中定义三⾓形的三个顶点的初始坐标和dAngle的初值，代码如下；CTransformView::CTransformView(){// TODO: add construction code herePt[0].x = 200; Pt[0].y = 220;Pt[1].x = 260; Pt[1].y = 300;Pt[2].x = 360; Pt[2].y = 180;dAngle = 0.0;}5、在类CTransformView中添加成员函数void DrawTriangle(CDC *pDC)，并实现该函数。
（该部分代码请同学们⾃⼰实现，为了简便编程，可以使⽤MoveTo和LineTo函数，也可以调⽤⾃⼰在实验2中编写的DDA或者Bresenham画线函数）；6、在类CTransformView的OnDraw()函数中添加绘制三⾓形的代码；void CTransformView::OnDraw(CDC* pDC){CTransformDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data here}7、映射菜单消息，⽅法是打开ResourceView菜单，依次展开MENU \ IDR_MAINFRAME，添加“图形变换”主菜单项，在其下添加“平移”，如图3所⽰。
实验五图形几何变换的实现班级 08信计2班学号 20080502057 姓名冯双捷分数一.实验目的和要求1.掌握二维、三维图形基本变换的变换原理；2.利用TurboC实现二维、三维图形的基本变换和符合变换3.屏幕显示变换过程和变换结果。
二.实验内容1.原程序实现二维图形（直线）的平移变换；=±（1）沿x轴的平移公式：'x x r=±（2）沿y轴的平移公式：'y y s2.源程序实现三维图形（立方体）的旋转变换和比例变换。
（1）旋转变换即图形围绕圆心逆时针旋转一定的角度；（2）比例变换即对象距圆点的距离按照一定比例进行变换。
三.实验结果分析1.二维平移程序代码#include <stdio.h>#include <graphics.h>#include <conio.h>int initjuzhen(m)int m[3][3];{int i,j;for(i=0;i<3;i++)for(j=0;j<3;j++)m[i][j]=0;for(i=0;i<3;i++)m[i][i]=1;}main(){int x0,y0,x1,y1,i,j;int a[3][3];char key;int graphdriver=DETECT;int graphmode=0;initgraph(&graphdriver,&graphmode," ");cleardevice();setcolor(2);x0=250;y0=120;x1=350;y1=220;line(x0,y0,x1,y1);for(;;){outtextxy(100,400,"<-:left ->:right^:up v:down Esc->exit");key=getch();initjuzhen(a);switch(key){case 75:a[2][0]=-10;break;case 77:a[2][0]=10;break;case 72:a[2][1]=-10;break;case 80:a[2][1]=10;break;case 27:exit();break;}x0=x0*a[0][0]+y0*a[1][0]+a[2][0];y0=x0*a[0][1]+y0*a[1][1]+a[2][1];x1=x1*a[0][0]+y1*a[1][0]+a[2][0];y1=x1*a[0][1]+y1*a[1][1]+a[2][1];clearviewport();line(x0,y0,x1,y1);}closegraph();}运行结果见文件夹：ERWEI2.三维图形旋转转换，比例变换程序代码：#include <stdio.h>#include <math.h>#include <graphics.h>#include <conio.h>#include <time.h>#include <ctype.h>#define ZOOM_IN 0.9#define ZOOM_OUT 1.1int turn1[3];typedef struct{float x;float y;float z;}point;typedef struct{float x;float y;}point2d;typedef struct{float x;float y;float h;point biao[8];}fanti;void make_box(float x,float y,float h,fanti *p) {p->x=x;p->y=y;p->h=h;p->biao[0].x=x/2;p->biao[0].y=y/2;p->biao[0].z=h/2;p->biao[1].x=-x/2;p->biao[1].y=y/2;p->biao[1].z=h/2;p->biao[2].x=-x/2;p->biao[2].y=-y/2;p->biao[2].z=h/2;p->biao[3].x=x/2;p->biao[3].y=-y/2;p->biao[3].z=h/2;p->biao[4].x=x/2;p->biao[4].y=y/2;p->biao[4].z=-h/2;p->biao[5].x=-x/2;p->biao[5].y=y/2;p->biao[5].z=-h/2;p->biao[6].x=-x/2;p->biao[6].y=-y/2;p->biao[6].z=-h/2;p->biao[7].x=x/2;p->biao[7].y=-y/2;p->biao[7].z=-h/2;}void turn2d(point *p,point2d *q){q->x=p->x+p->z*cos(0.25);q->y=p->y+p->z*sin(0.25);}void initm(float mat[][4]){int count;for(count=0;count<4;count++){mat[count][0]=0.;mat[count][1]=0.;mat[count][2]=0.;mat[count][3]=0.;mat[count][count]=1.;}return;}void transform(point *p,point *q,float tm[][4]){float xu,yv,zw,h;xu=tm[0][0]*p->x+tm[1][0]*p->y+tm[2][0]*p->z+tm[3][0];yv=tm[0][1]*p->x+tm[1][1]*p->y+tm[2][1]*p->z+tm[3][1];zw=tm[0][2]*p->x+tm[1][2]*p->y+tm[2][2]*p->z+tm[3][2];p->x=xu;p->y=yv;p->z=zw;return;}void rotationx(point *p,float alfa,float tm[][4]){float rad=0.0174532925;initm(tm);tm[1][1]=cos(rad*alfa);tm[1][2]=sin(rad*alfa);tm[2][1]=-tm[1][2];tm[2][2]=tm[1][1];return;}void rotationz(point *p,float alfa,float tm[][4]){float rad=0.0174532925;initm(tm);tm[0][0]=cos(rad*alfa);tm[0][1]=sin(rad*alfa);tm[1][0]=-tm[0][1];tm[1][1]=tm[0][0];return;}void rotationy(point *p,float alfa,float tm[][4]) {float rad=0.0174532925;initm(tm);tm[0][0]=cos(rad*alfa);tm[2][0]=sin(rad*alfa);tm[0][2]=-tm[2][0];tm[2][2]=tm[0][0];return;}void adjust(point *p,point *q){float t[4][4];switch(turn1[0]){case 1:rotationy(p,2,t);transform(p,q,t);break;case -1:rotationy(p,-2,t);transform(p,q,t);break;default:break;}switch(turn1[1]){case 1:rotationz(p,2,t);transform(p,q,t);break;case -1:rotationz(p,-2,t);transform(p,q,t);break;default:break;}switch(turn1[2]){case 1:q->x=ZOOM_IN*p->x;q->y=ZOOM_IN*p->y;q->z=ZOOM_IN*p->z;break;case -1:q->x=ZOOM_OUT*p->x;q->y=ZOOM_OUT*p->y;q->z=ZOOM_OUT*p->z;break;default:break;}}void drawbox(fanti *p){point2d fan2d[8];int i;for(i=0;i<=7;i++){adjust(&p->biao[i],&p->biao[i]);turn2d(&p->biao[i],&fan2d[i]);fan2d[i].x+=300;fan2d[i].y+=200;}clearviewport();setcolor(2);outtext("\n ->:right\n <-:left\n ^:up\n v:down");moveto(0,10);outtext("\n page up:zoom in\n page down:zoom out\n space:Redraw\n Esc:exit");for(i=0;i<=3;i++){if(i==3){line(fan2d[i].x,fan2d[i].y,fan2d[0].x,fan2d[0].y);line(fan2d[i+4].x,fan2d[i+4].y,fan2d[4].x,fan2d[4].y);}else{line(fan2d[i].x,fan2d[i].y,fan2d[i+1].x,fan2d[i+1].y);line(fan2d[i+4].x,fan2d[i+4].y,fan2d[i+5].x,fan2d[i+5].y);}line(fan2d[i].x,fan2d[i].y,fan2d[i+4].x,fan2d[i+4].y);}}void main(){int gd=DETECT,gm,i,j;char key;float x,y,h;fanti a1;x=100;y=100;h=100;initgraph(&gd,&gm," ");make_box(x,y,h,&a1);drawbox(&a1);for(;;){turn1[0]=0;turn1[1]=0;turn1[2]=0;key=getch();switch(key){case 77:turn1[0]=1;break;case 75:turn1[0]=-1;break;case 72:turn1[0]=1;break;case 80:turn1[0]=-1;break;case 73:turn1[2]=1;break;case 81:turn1[2]=-1;break;case 32:make_box(x,y,h,&a1);break;case 27:exit();break;default:key=0;break;}if(key!=0)drawbox(&a1);}closegrapg();}运行结果见文件夹：SANWEI3.分析使用矩阵保存图形的坐标位置的方法，二维图形的平移就是一个坐标位置移到另一个坐标位置的重定位过程；对于三维的图形的旋转变换就是图形相应的矩阵进行角度的初等变换，而比例变换即是图形矩阵的相应比例变换。
计算机图形学实验报告课程名称: 计算机图形学实验名称:图形绘制与变换学院: 电子信息工程学院专业: 计算机科学与技术班级: 11计科本01班学号: ************ **: ******: ***二零一四年目录一、引言----------------------------------------------------------------------- 3二、设计需求------------------------------------------------------------------- 32.1 设计目标 -------------------------------------------------------------- 32.2 设计环境 -------------------------------------------------------------- 32.2.1 VC++6.0 ------------------------------------------------------- 32.2.2 MFC ----------------------------------------------------------- 42.3 设计题目及要求 ------------------------------------------------------- 42.4 总体流程图 ----------------------------------------------------------- 4三、课程设计原理--------------------------------------------------------------- 53.1 实现的算法 ------------------------------------------------------------ 53.1.2 Bresenham算法画直线-------------------------------------------- 63.1.3 中心点算法画圆和椭圆-------------------------------------------- 63.2 图形变换的基本原理 ---------------------------------------------------- 83.2.1 平移变换 -------------------------------------------------------- 83.2.2 旋转变换 ------------------------------------------------------- 83.2.3 比例变换 ------------------------------------------------------- 8四、总体设计与功能实现--------------------------------------------------------- 94.1 主要界面设计 ---------------------------------------------------------- 94.2 设置颜色界面 ---------------------------------------------------------- 94.2.1 界面设置代码 ---------------------------------------------------- 94.2.2 运行结果 ------------------------------------------------------- 104.3 二维线画图元实现 ----------------------------------------------------- 104.4 画多边形功能的实现 -------------------------------------------------- 144.5 画Bezier曲线功能的实现--------------------------------------------- 154.6 二维图形变换的实现 -------------------------------------------------- 164.7 三维图形的变换 ------------------------------------------------------ 18五、实验心得体会一、引言计算机图形学(Computer Graphics，简称CG)是一种使用数学算法将二维或三维图形转化为计算机显示器的栅格形式的科学。
简单地说，计算机图形学的主要研究内容就是研究如何在计算机中表示图形、以及利用计算机进行图形的计算、处理和显示的相关原理与算法。
是计算机科学的一个分支领域，主要关注数字合成与操作视觉的图形内容。
计算机图形学研究的是应用计算机产生图像的所有工作，不管图像是静态的还是动态的，可交互的还是固定的，等等。
图形API是允许程序员开发包含交互式计算机图形操作的应用而不需要关注图形操作细节或任务系统细节的工具集。
计算机图形学有着广泛的应用领域，包括物理、航天、电影、电视、游戏、艺术、广告、通信、天气预报等几乎所有领域都用到了计算机图形学的知识，这些领域通过计算机图形学将几何模型生成图像，将问题可视化从而为各领域更好的服务。
计算机图形学利用计算机产生让人赏心悦目的视觉效果，必须建立描述图形的几何模型还有光照模型，再加上视角、颜色、纹理等属性，再经过模型变换、视图变换、投影操作等，这些步骤从而实现一个完整的OpenGL程序效果。
OpenGL是一个开放的三维图形软件包，它独立于窗口系统和操作系统，以它为基础开发的应用程序可以十分方便地在各种平台间移植。
计算机图形学通过应用OpenGL的功能，使得生成的图形效果具有高度真实感。
学习计算机图形学的重点是掌握OpenGL在图形学程序中的使用方法。
事实上，图形学也把可以表示几何场景的曲线曲面造型技术和实体造型技术作为其主要的研究内容。
同时，真实感图形计算的结果是以数字图像的方式提供的，计算机图形学也就和图像处理有着密切的关系。
通过21世纪是信息的时代，在日新月异的科技更新中相信计算机会发挥越来越重要的作用，计算机图形学也会在更多的领域所应用，虽然我国在这方面还比较薄弱，但相信会有越来越好的时候的。
二、设计需求2.1 设计目标以图形学算法为目标，深入研究。
继而策划、设计并实现一个能够表现计算机图形学算法原理的或完整过程的演示系统，并能从某些方面作出评价和改进意见。
通过完成一个完整程序，经历策划、设计、开发、测试、总结和验收各阶段，达到：巩固和实践计算机图形学课程中的理论和算法；学习表现计算机图形学算法的技巧；培养认真学习、积极探索的精神。
2.2 设计环境2.2.1 VC++6.0VC++6.0是Microsoft 公司推出的一个基于Windows 系统平台、可视化的集成开发环境，它的源程序按C++语言的要求编写，并加入了微软提供的功能强大的MFC(MicrosoftFoundation Class)类库。
MFC 中封装了大部分Windows API 函数和Windows 控件，它包含的功能涉及到整个Windows 操作系统。
MFC 不仅给用户提供了Windows 图形环境下应用程序的框架，而且还提供了创建应用程序的组件，这样，开发人员不必从头设计创建和管理一个标准Windows 应用程序所需的程序，而是从一个比较高的起点编程，故节省了大量的时间。
另外，它提供了大量的代码，指导用户编程时实现某些技术和功能。
因此，使用VC++提供的高度可视化的应用程序开发工具和MFC 类库，可使应用程序开发变得简单。
2.2.2 MFCMFC(Microsoft Foundation Classes) ，是一个微软公司提供的类库（class libraries）以C++类的形式封装了Windows 的API，，它包含了窗口等许多类的定义。
各种类的集合构成了一个应运程序的框架结构，以减少应用程序开发人员的工作量。
其中包含的类包含大量Windows 句柄封装类和很多Windows 的内建控件和组件的封装类。
MFC 6.0 版本封装了大约200 个类，其中的一些可以被用户直接使用。
例如CWnd 类封装了窗口的功能，包括打印文本、绘制图形及跟踪鼠标指针的移动等；CsplitterWnd 类是从CWnd 类派生出来的，继承了基类或称父类CWnd 类的所有特性，但增加了自己的功能，实现拆分窗口，使窗口至少可被拆分成两个窗口，用户可以移动两个窗口之间的边框来改变窗口的大小；CtoolBar 类可以定义工具栏等。
MFC 命名的惯例是类的名字通常是由“C”打头；成员变量使用前缀“m_”，接着使用一个字母来指明数据类型，然后是变量的名称；所有的单词用大写字母开头。
2.3 设计题目及要求（1）题目：实现多边形和曲线的绘制和变换（2）要求：学会使用VC++编写实现图形的绘制变换，需包括直线、曲线、多边形的绘制和变换，及三维立体图形的相应变换.2.4 总体流程图三、课程设计原理3.1 实现的算法3.1.1 DDA算法画直线DDA是数字微分分析式（Digital Differential Analyzer）的缩写。
已知直线两端点(x1,y1)、(x2,y2)则斜率m为：m = (y2-y1)/(x2-x1)= Dx/Dy;直线中的每一点坐标都可以由前一点坐标变化一个增量（Dx, Dy）而得到，即表示为递归式：xi+1=xi+Dx yi+1=yi+Dy 。
递归式的初值为直线的起点（x1, y1），这样，就可以用加法来生成一条直线。
具体算法是：该算法适合所有象限，其中用了用了两个函数如：Integer(-8.5)= -9; Integer(8.5) =8;Sign(i),根据i的正负，分别得到-1，0，+1；相应代码：//DDA DrawLine{if(abs(x2-x1) > abs(y2-y1))length = abs(x2-x1);elselength = abs(y2-y1);Dx = (x2-x1)/length;Dy = (y2-y1)/length;x = x1+0.5*Sign(Dx); y = x2 + 0.5*Sign(Dy); i = 1;while(i <= lenght){ setpixel(Integer(x),Integer(y),color); x= x + Dx; y= y + Dy; i+=1;} }3.1.2 Bresenham 算法画直线思路如下:// 假设该线段位于第一象限内且斜率大于0小于1,设起点为(x1,y1),终点为(x2,y2). // 根据对称性,可推导至全象限内的线段.1.画起点(x1,y1).2.准备画下个点。
