数字信号处理第三章作业.pdf

格式：pdf
大小：287.03 KB
文档页数：5

下载文档原格式

数字信号处理第三章

j
：相位函数（phase function）或相位谱（phase spectrum）
3/29
与连续时间傅立叶变换的关系
X (W) = xa ( t ) =
ò
+¥ -¥
x (t )e - jWt dt
k =-¥
å x(k )d (t - k )
X ( W) =
+¥
ò
+¥ -¥
X * (e j )
1 X cs (e j ) { X (e j ) X * (e j )} 2 1 X ca (e j ) { X (e j ) X * (e j )} 2
xcs [n] xca [n]
X re (e j ) jX im (e j )
16/29
K
lim
X e X e d 0

j K j 2
例：理想低通滤波器 1 0 c H LP e 0 c j c n j c n 1 c jn 1 e e sin c n hLP n e d 2 c 2 jn n jn
10/29
3.1.2 收敛条件（convergence)
如果x[n]的DTFT在种意义上收敛，则称x[n]的傅立叶变换存在
1、一致收敛（uniform convergence）令X K e j
xne ，一致收敛的定义为 lim X e X e 0
Table 3.4 实序列的离散时间傅立叶变换的对称关系序列离散时间傅立叶变换
x[n]
xev [n]
X (e j ) X re (e j ) jX im (e j )

数字信号处理-第3版-答案(PDF)

第二章
2.1 判断下列序列是否是周期序列。若是，请确定它的最小周期。（1）x(n)=Acos( （2）x(n)= e (
j
π 5π n+ ) 8 6
n −π) 8 π 3π （3）x(n)=Asin( n+ ) 4 3
(1)对照正弦型序列的一般公式 x(n)=Acos( ωn + ϕ )，得出 ω =
k = −∞
∑ u (k ) a
∞
n−k
u (n − k ) =
k = −∞
∑a
∞
n−k
=
1 − a n +1 u(n) 1− a
2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)= λ
n
u(n)*u(n)
解：(1)
y(n)=
k = −∞ ∞
∑ u(k )u(n − k )
π 2π (n-k)+ ]| 3 6 π 2π =|x(n)|| sin[ (n-k)+ ]| 3 6
≤M|sin[
π 2π (n- k)+ ]|≤M 3 6
故系统是稳定系统。因 y(n)只取决于现在和过去的输入 x(n),不取决于未来的输入，故该系统是因果系统。（3）设 y1(n)=
k = −∞
−n
u(-n),0<a<1 用直接计算线性卷积的方法，求
2.6 试证明线性卷积满足交换率、结合率和加法分配率。
证明
（1）交换律 X(n) * y(n) =
k = −∞
∑ x(k ) y (n − k )
∞
令 k=n-t,所以 t=n-k,又- ∞ <k< ∞ ,所以- ∞ <t< ∞ ,因此线性卷积公式变成

《数字信号处理》作业程佩青(第2版)清华大学出版社课后答案

0.588
0.5
0
0
0
0
-0.5 -0.588
-1 -0.951
-0.588
-0.951
-1.5 0 1 2 3 4 5 6 7 8 9 10
绘图程序如下： n = 0:10; % 定义时间长度 xa = cos(40*pi*n*0.02 + pi/2); stem(n,xa,'filled'),title('cos(40*\pi*n*0.02 + \pi/2)') axis([-1,n(end)+1,-1.5,1.5]) for i = 1:11
N −1
∑ X (k) = −
[ x(( N
−1−
n))N
RN
(n)WN−
k
(
N
W −1−n) k N
(
N
−1)
]
n=0
N −1
∑ = − [x(n)N WN−kn ]WNk (N −1) n=0
N −1
∑ = − [x(n)N WN(−k )n ] •WNk (N −1) n=0
N −1
∑ = − [x(n)N WN(−k )n ] •WNk (N −1) n=0
课后答案网
2.8 P140 题 10
12 3 4 0 00 -1 -1 -1 -1 -1 1 1 1 2 3 40 00 1 2 3 4 00 0 -1 -2 -3 -4 0 0 0 -1 -2 -3 -4 0 0 0 -1 -2 -3 -4 0 0 0 -1 -2 -3 -4 0 0 0 -1 -2 -3 -4 0 0 0 -1 -3 -6 -10 -10 -8 -4 1 7 4 0 0 0 -1 -3 -6 -10 -10 -8 -4 17 40 0 0 0 4 -2 -10 -10 -8 -4

数字信号处理第三版(姚天任、江太辉) 答案第三章

第三章离散傅里叶变换及其快速算法习题答案参考
3.1 图 P3.1 所示的序列 x(n) 是周期为 4 的周期性序列。请确定其傅里叶级数的系数 X (k) 。
∑ ∑ ∑ 解： X (k)
=
N −1
x(n)WNnk
=
N −1
x(−n)WNnk
=
−( N −1)
x(n)WN−nk
=
X (−k)
解：图 P3.5_1 所示的是计算这两个序列的周期卷积 x3 (n) 的过程，可以看出，x3 (n) 是 x1 (n) 延时 1 的结果，即 x3(n) = x1(n −1) 。
3.6 计算下列序列的N点DFT：
(1) x(n) = δ (n)
(2) x(n) = δ [(n − n0 )]N * RN (n), 0 < n0 < N
总计需要时间： (105 + 21)s = 126s
用 FFT 计算 DFT：
复数乘法：
N 2
log2
N
=
5120次, 5120 ×100μ s
≈
0.512s
复数加法： N log2 N = 10240次,10240× 20μs ≈ 0.2048s
总计需要时间： (0.512 + 0.2048)s = 0.7168s
（2） x2 (n) = x ⎡⎣(2 − n)⎤⎦4 R4 (n)
解： x1(n) 和 x2 (n) 的图形如图 P3.7_1 所示：
3.8 图 P3.8 表示一个 4 点序列 x(n) 。（1）绘出 x(n) 与 x(n) 的线性卷积结果的图形。（2）绘出 x(n) 与 x(n) 的 4 点循环卷积结果的图形。（3）绘出 x(n) 与 x(n) 的 8 点循环卷积结果的图形，并将结果与（1）比较，说明线性卷积与循环卷

数字信号处理第三版(姚天任、江太辉) 答案第三章

第三章离散傅里叶变换及其快速算法习题答案参考3.1 图P3.1所示的序列(xn 是周期为4的周期性序列。

请确定其傅里叶级数的系数(X k。

解:(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.2 (1设(xn 为实周期序列,证明(x n 的傅里叶级数(X k 是共轭对称的,即*((X k X k =− 。

(2证明当(xn 为实偶函数时,(X k 也是实偶函数。

证明:(1 111**((([(]((N nk N n N N nk nkNNn n Xk x n W Xk x n W xn W X−−=−−−==−=−===∑∑∑ k(2因(xn 为实函数,故由(1知有 *((Xk X k =− 或*((X k X k −= 又因(xn 为偶函数,即((x n x n =− ,所以有(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.3 图P3.3所示的是一个实数周期信号(xn 。

利用DFS 的特性及3.2题的结果,不直接计算其傅里叶级数的系数(Xk ,确定以下式子是否正确。

(1,对于所有的k; ((10Xk X k =+ (2((Xk X k =− ,对于所有的k; (3; (00X=(425(jkX k eπ,对所有的k是实函数。

解:(1正确。

因为(x n 一个周期为N =10的周期序列,故(X k 也是一个周期为N=10的周期序列。

(2不正确。

因为(xn 一个实数周期序列,由例3.2中的(1知,(X k 是共轭对称的,即应有*((Xk X = k −,这里(X k 不一定是实数序列。

(3正确。

因为(xn (0n ==在一个周期内正取样值的个数与负取样值的个数相等,所以有 10(0N n Xx −=∑ (4不正确。

第三章Z变换(数字信号处理)

n2
X (z) x(n)zn
n
第三章序列的Z变换
当 n2≤0
n2
n2
n2
X (Z ) x(n)Z n x(n)Z n x(n) Rn
n
n
n
当 n2>0
n2
0
n2
x(n)Z n x(n)Z n x(n)Z n
n
n
n 1
第二项为有限长序列，在整个Z平面收敛（ z=∞点不收敛）。第一项根据前式的论述，当
第三章序列的Z变换
n 0, x(n) Re s[F(z), a] Re s[F(z), a1]
a(
(1 a2 z a)(
)zn z
a
1
)
(
z
a)
za
a(
(1 a2 z a)(
)zn z
a
1
)
(
z
a1)
z a 1
an (an ) an an
最后将x(n)表示成
x(n)=(a-n-an)u(-n-1)
(1 a2 )zn (z a) (z a)(1 az)
za
a(
(1 a2 z a)(
)zn z
a
1
)
(
z
a
1 )
z a 1
an an
最后表示成： x(n)=(an-a-n)u(n)。
(2) 收敛域|z|<|a|
这种情况原序列是左序列，无须计算n≥0情况，当n≥0时，围线积分c内没有极点，因此x(n)=0。 n<0 时， c内只有一个极点z=0，且是n阶极点，改求c外极点留数之和
Z R 时收敛因此左序列的收敛域是半径为R+的圆内区域

数字信号处理课后第三章习题答案

1 e j 0 N
2 j(0 k ) N 1 e
k 0, 1, , N 1
（8）解法一
直接计算：
1 j 0 n x8 (n) sin(0 n) RN (n) [e e j 0 n ] R N ( n ) 2j
X 8 (n)

n 0
N 1
kn x8 (n)WN
k 0, 1, , N 1
(4)
X (k ) WNkn
n 0
m1
π j ( m1) k 1 WNkm N e 1 WNk
π sin mk N R (k ) N π sin k N
第３章
离散傅里叶变换(DFT)及其快速算法 (FFT)
所以
DFT[ X (n)] X (n)W
n 0
N 1
N 1
kn N
N 1 mn kn x(m)WN WN n 0 m 0
N 1
n ( m k ) x(m)WN m 0 n 0
N 1
第３章
由于
离散傅里叶变换(DFT)及其快速算法 (FFT)
第３章
离散傅里叶变换(DFT)及其快速算法 (FFT)
（10）解法一
X (k )

n 0
N 1
kn nWN
k 0, 1, , N 1
上式直接计算较难，可根据循环移位性质来求解X(k)。因为x(n)=nRN(n)，所
以
x(n)－x((n－1))NRN(n)+Nδ(n)=RN(n) 等式两边进行DFT，得到
1 [e j0 n e j0 n ] e 2 j n 0

数字信号处理第三章习题作业答案

1 e 当 k 2, 4, 6,... 时，X 1 (k ) 0

序列3:
x3 (n) x1 (n) x1 (n 4)
根据序列移位性质可知
X 3 (k ) X1 ( k ) e j k X1 ( k ) (1 e j k )
即 x(n) 是以 n 0 对称轴的奇对称
故这三个序列都不满足这个条件
（3）由于是8点周期序列，其DFS:
nk X (k ) x(n )WN x (n )e n 0 n 0 N 1 7 j 2 nk 8
序列1:
X 1 (k ) e
n 0
3
y 解: 序列 x(n) 的点数为 N1 6 ， (n) 的点数为 N 2 15，故 x(n) y (n) 的点数应为
N N1 N 2 1 20
是线性卷积以15为周期周期延拓后取主值序列 19( N 1) 0
15 ( L)
又 f (n) 为 x(n) 与 y (n) 的15点的圆周卷积，即L＝15。
第三章习题讲解
n 1, 0 n 4 h(n) R4 (n 2) 3．设 x(n) 其他n 0, h 令 x(n) x((n))6 ， ( n) h((n)) 6 ，
试求 x(n) 与 h (n) 的周期卷积并作图。
解：
y ( n ) x ( m )h ( n m )
4 ( L N 1)
15 ( L)
34 ( L N 1)
混叠点数为N－L＝20－15＝5 n 0 ~ n 4( N L 1) 故 f (n)中只有 n 5到 n 14的点对应于 x(n) y (n)

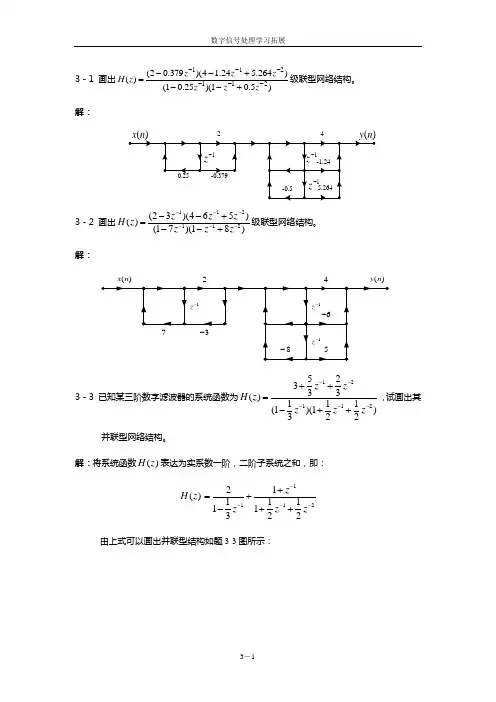
数字信号处理(方勇)第三章习题答案

3－1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz zzzz H 级联型网络结构。

解：243－2 画出112112(23)(465)()(17)(18)z z zH z z zz--------+=--+级联型网络结构。

解：()x n ()y n 243－3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322zzH z z zz-----++=-++，试画出其并联型网络结构。

解：将系统函数()H z 表达为实系数一阶，二阶子系统之和，即：()H z 11122111111322z zzz----+=+-++由上式可以画出并联型结构如题3-3图所示：)题3-3图3－4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z z z z ---=-++，画出该FIR滤波器的线性相位结构。

解：因为121123()(10.70.5)(12)1 1.30.9H z z z z z z z ------=-++=+-+，所以由第二类线性相位结构画出该滤波器的线性相位结构，如题3-4图所示：()x n 1-1-1z -题3-4图3－5 已知一个FIR 系统的转移函数为：12345()1 1.25 2.75 2.75 1.23H z zzzzz-----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。

解：由转移函数可知，6=N ，且)(n h 偶对称，故为线性相位系统，共有5个零点，为5阶系统，因而必存在一个一阶系统，即1±=z 为系统的零点。

而最高阶5-z 的系数为+1，所以1-=z 为其零点。

)(z H 中包含11-+z 项。

所以：11()()(1)H z H z z -=+。

1()H z 为一四阶子系统，设12341()1H z bz cz bz z ----=++++，代入等式，两边相等求得12341()10.2530.25H z z z z z ----=+-++，得出系统全部零点，如图3-5（b ）所示。

《数字信号处理》第三版答案(非常详细完整)

答案很详细，考试前或者平时作业的时候可以好好研究，祝各位考试成功！！电子科技大学微电子与固体电子学陈钢教授著数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3)0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6()6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如 5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

（1）()()2(1)3(2)y n x n x n x n =+-+-；（3）0()()y n x n n =-，0n 为整常数；（5）2()()y n x n =；（7）0()()nm y n x m ==∑。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数字信号处理第三章作业
1．(第三章习题3)在图P3-2中表示了两个周期都为6的周期性序列，确定这个两个序列的周期卷积的结果3()x n ，并画出草图。

2．(第三章习题5)如果()x n 是一个具有周期为N 的周期性序列，它也是具有周期为2N 的周期性序列。

令~1()X k 表示当()x n 看做是具有周期为N 的周期性序列的DFS 系数。

而~2()X k 表示当()x n 看作是具有周期为2N 的周期性序列的DFS 系数。

当然~1()X k 是具有周期为N 的周期性序列，而~2()X k 是具有周期为2N 的周期性序列，试根据~1()X k 确定~2()X k 。

3．(第三章习题6)
（a ）试证明下面列出的周期性序列离散傅里叶级数的对称特性。

在证明中，可以利用离散傅里叶级数的定义及任何前面的性质，例如在证明性质③时可以利用性质①和②。

序列
离散傅里叶级数 ① *()x n
~*()X k - ②*()x n -
~*()X k ③Re ()x n ⎡⎤⎣⎦
~
e ()X k ④Im ()j x n ⎡⎤⎣⎦ ~()o X k
（b ）根据已在（a ）部分证明的性质，证明对于实数周期序列()x n ，离散傅里叶级数的下列对称性质成立。

①~~Re ()Re ()X k X k ⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦
②~~Im ()Im ()X k X k ⎡⎤⎡⎤=--⎢⎥⎢⎥⎣⎦⎣⎦
③~~()()X k X k =- ④~~arg ()arg ()X k X k ⎡⎤⎡⎤=--⎢⎥⎢⎥⎣⎦⎣⎦
4．(第三章习题7)求下列序列的DFT
(a) {}11
1-，，，-1 (b) {}1
j 1j -，，，- (c) ()cn 0n 1x n N =≤≤-，
(d) 2n ()sin 0n 1x n N N π⎛⎫=≤≤- ⎪⎝⎭
， 5．(第三章习题8)计算下列各有限长序列的离散傅立叶变换（假设长度为N ）
1
0)()(0)
()()()
()()(00-≤≤=<<-==N n a n x c N n n n n x b n n x a n δδ 6．(第三章习题9)在图P3-4中表示了一有限长序列)(n x ，画出序列)(1n x 和)(2n x 的草图。

（注意：)(1n x 是)(n x 圆周移位两个点）
)())(()()
())2(()(442441n R n x n x n R n x n x -=-=
7．(第三章习题10)在图P3-5中表示了两个有限长序列，试画出它们的六点圆周卷积。

11．有限长序列的DFT 对应于序列在单位圆上的z 变换的取样。

例如一个10点序列)(n x 的DFT 对应于图P3-6-1表示的10个等间隔点上)(z X 的取样。

我们希望找出在图P3-6-2所示的围线上)(z X 的等间隔取样，即)]10()102[(5.0|)(ππ+=k j e z z X 。

证明如何修改)(n x 以获得一个序列)(1n x 致使)(1n x 的DFT 对应于所希望的)(z X 的取样。

8．(第三章习题13)列长为8的一个有限长序列列具有8点离散傅里叶变换X(k)，如图P3-7-1所示。

列长为16点的一个信号的序列y(n)定义为：
n n ⎧ ⎪⎨⎪
⎩n x()为偶数y(n)=2
0为奇数试从P3-7-2的几个图中选出相当于y(n)的16点离散傅里叶变换序列图。

9．(第三章习题14)图P3-8表示一个四点序列x(n)
(a)试绘出x(n)同x(n)线性卷积略图
(b)试绘出x(n)同x(n)四点圆周卷积略图
(c)试绘出x(n)同x(n)十点圆周卷积略图
(d)若x(n)同x(n)的某个N点圆周卷积同其线性卷积相同，试问此时N点的最小值是多少？
10. (第三章习题15)研究两个有限长序列x(n)和y(n)，此二序列当n<0时皆为零，并且
各作其20点DFT，然后将两个DFT相乘，再计算其乘积序列的逆DFT，设r(n)表示逆DFT，试指出r(n)哪些点对应于x(n)与y(n)作线性卷积应得到的点。

11.(第三章习题16)现有一为随机信号谱分析所使用的处理器，该处理器使用的取样点数必须是2的整数次方，并假设没有采取任何特特殊的数据处理措施。

已给条件是：(1) 频率的分辨率5Hz，(2)信号的最高频率 1.25kHz，要求确定下列参量：(a)最小记录长度；(b)取样点间的最大时间间隔；(c)在一个记录中的最少点数。

数字信号处理第三章作业.pdf

合集下载