人教版几何模型基本图形

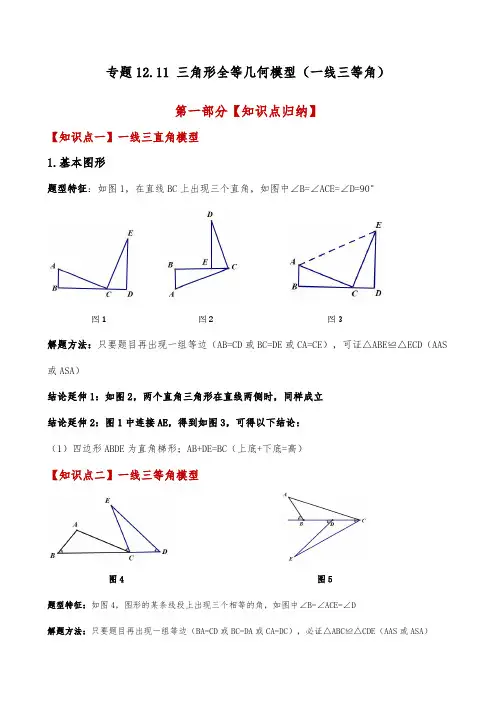
专题12.11三角形全等几何模型（一线三等角）第一部分【知识点归纳】【知识点一】一线三直角模型1.基本图形题型特征：如图1，在直线BC上出现三个直角，如图中∠B=∠ACE=∠D=90°图1图2图3解题方法：只要题目再出现一组等边（AB=CD或BC=DE或CA=CE），可证△ABE≌△ECD（AAS 或ASA）结论延伸1：如图2，两个直角三角形在直线两侧时，同样成立结论延伸2：图1中连接AE，得到如图3，可得以下结论：（1）四边形ABDE为直角梯形；AB+DE=BC（上底+下底=高）【知识点二】一线三等角模型图4图5题型特征：如图4，图形的某条线段上出现三个相等的角，如图中∠B=∠ACE=∠D解题方法：只要题目再出现一组等边（BA=CD或BC=DA或CA=DC），必证△ABC≌△CDE（AAS或ASA）结论延伸：如图5，两个三角形在直线两侧时，同样成立第二部分【题型展示与方法点拨】【题型1】直接用“一线三直角”模型求值或证明【例1】（23-24八年级上·安徽合肥·期末）如图，在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C ，且AD MN ⊥，BE MN ⊥，垂足分别为D E 、．（1）求证：ADC CEB ≌；（2）若3cm =AD ，5cm BE =，求四边形ABED 的面积．【变式1】（23-24八年级上·湖北武汉·阶段练习）如图，小虎用10块高度都是3cm 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC BC =，90ACB ∠=︒），点C 在DE 上，点A 和B 分别与木墙的顶端重合，则两堵木墙之间的距离DE 的长度为（）A ．30cmB ．27cmC ．21cmD ．10cm【变式2】（23-24九年级下·重庆开州·阶段练习）如图，在Rt ABC 中，90BAC ∠=︒，AB AC =，点D 为BC 上一点，连接AD ．过点B 作BE AD ⊥于点E ，过点C 作CF AD ⊥交AD 的延长线于点F ．若5BE =，2CF =，则EF 的长度为．【题型2】直接用“一线三等角”模型求值或证明【例2】（23-24八年级上·新疆昌吉·期中）已知ABC 是直角三角形，90BAC AB AC ∠=︒=，，直线l 经过点A ，分别过点B 、C 向直线l 作垂线，垂足分别为D 、E（1）如图a ，当点B 、C 位于直线l 的同侧时，证明：ABD CAE≌（2）如图b ，锐角ABC 中，AB AC =，直线l 经过点A ，点D 、E 分别在直线l 上，点B ，C 位于l 的同一侧，如果CEA ADB BAC ∠=∠=∠，请找到图中的全等三角形，并写出线段ED EC 、和DB 之间的数量关系【变式1】（21-22八年级上·浙江温州·期中）如图，在△ABC 中，AB ＝AC ＝9，点E 在边AC 上，AE 的中垂线交BC 于点D ，若∠ADE ＝∠B ，CD ＝3BD ，则CE 等于（）A ．3B ．2C ．94D ．92【变式2】（23-24七年级下·吉林长春·期中）如图，在ABC 中，AB AC =，AB BC >，点D 在边BC 上，且2CD BD =，点E 、F 在线段AD 上．CFD BED BAC ∠=∠=∠，ABC 的面积为18，则ABE 与CDF 的面积之和．【题型3】构造“一线三直角”模型求值或证明【例3】（23-24八年级上·山西吕梁·期末）数学课上，老师让同学们利用三角形纸片进行操作活动，探究有关线段之间的关系问题情境：如图1，三角形纸片ABC 中，90ACB ∠=︒，AC BC =.将点C 放在直线l 上，点A ，B 位于直线l 的同侧，过点A 作AD l ⊥于点D初步探究：（1）在图1的直线l 上取点E ，使BE BC =，得到图2，猜想线段CE 与AD 的数量关系，并说明理由；（2）小颖又拿了一张三角形纸片MPN 继续进行拼图操作，其中90MPN ∠=︒，MP NP =.小颖在图1的基础上，将三角形纸片MPN 的顶点P 放在直线l 上，点M 与点B 重合，过点N 作NH l ⊥于点H .如图3，探究线段CP ，AD ，NH 之间的数量关系，并说明理由【变式1】（23-24八年级上·新疆喀什·期中）如图，906AC AB BD ABD BC ==∠=︒=，，，则BCD △的面积为（）A ．9B ．6C ．10D ．12【变式2】（20-21七年级下·黑龙江哈尔滨·期末）如图，在ABC 中，90ABC ∠=︒，过点C 作CD AC ⊥，且CD AC =，连接BD ，若92BCD S = ，则BC 的长为．【题型4】“一线三直（等）角”模型的延伸与拓展【例4】如图，A 点的坐标为（0，3），B 点的坐标为（-3.0），D 为x 轴上的一个动点，AE ⊥AD ，且AE=AD ，连接BE 交y 轴于点M（1）若D点的坐标为（-5.0），求E点的坐标:（2）求证:M为BE的中点（3）当D点在x轴上运动时，探索:OMBD为定值【变式1】（23-24八年级上·陕西西安·阶段练习）勾股定理被誉为“几何明珠”．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图所示，把一个边长分别为3，4，5的三角形和三个正方形放置在大长方形ABCD中，则该长方形中空白部分的面积为（）A．54B．60C．100D．110【变式2】已知：四边形ABCD中，AB=AD=CD，∠BAD=90°，三角形ABC的面积为1，则线段AC的长度是.第三部分【中考链接与拓展延伸】1、直通中考【例1】（2021·四川南充·中考真题）如图，90BAC ∠=︒，AD 是BAC ∠内部一条射线，若AB AC =，BE AD ⊥于点E ，CF AD ⊥于点F ．求证：AF BE =．【例2】（2023·重庆·中考真题）如图，在Rt ABC △中，90BAC ∠= ，AB AC =，点D 为BC 上一点，连接AD ．过点B 作BE AD ⊥于点E ，过点C 作CF AD ⊥交AD 的延长线于点F ．若4BE =，1CF =，则EF 的长度为．2、拓展延伸【例1】（22-23八年级下·河南洛阳·期中）综合与实践数学活动课上，老师让同学们以“过等腰三角形顶点的直线”为主题开展数学探究．（1）操作发现：如图甲，在Rt ABC △中，90BAC ∠=︒，且AB AC =，直线l 经过点A ．小华分别过B 、C 两点作直线l 的垂线，垂足分别为点D 、E ．易证ABD CAE △△≌，此时，线段DE 、BD 、CE 的数量关系为：；（2）拓展应用：如图乙，ABC 为等腰直角三角形，90ACB ∠=︒，已知点C 的坐标为(2,0)-，点B 的坐标为(1,2)．请利用小华的发现直接写出点A 的坐标：；（3）迁移探究：①如图丙，小华又作了一个等腰ABC ，AB AC =，且90BAC ∠≠︒，她在直线l 上取两点D 、E ，使得BAC BDA AEC ∠=∠=∠，请你帮助小华判断（1）中线段DE 、BD 、CE 的数量关系是否变化，若不变，请证明；若变化，写出它们的关系式并说明理由；②如图丁，ABC 中，2AB AC =，90BAC ∠≠︒，点D 、E 在直线l 上，且BAC BDA AEC ∠=∠=∠，请直接写出线段DE 、BD 、CE 的数量关系．【例2】（22-23八年级上·广东惠州·期中）如图1，90ACB AC BC AD CE BE CE ∠==⊥⊥，，，，垂足分别为D ，E ．（1）若 2.5cm 1.7cm AD DE ==，，求BE 的长．（2）在其它条件不变的前提下，将CE 所在直线变换到ABC 的外部（如图2），请你猜想AD DE BE ，，三者之间的数量关系，并证明你的结论；（3）如图3，将（1）中的条件改为：在ABC 中，AC BC =，D ，C ，E 三点在同一条直线上，并且有BEC ADC BCA α∠=∠=∠=，其中α为任意钝角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．。

九年级数学几何模型一、相似三角形模型。

1. A字模型。

- 基本图形：在三角形ABC中，DE平行于BC，则三角形ADE相似于三角形ABC。

- 性质：对应边成比例，即(AD)/(AB)=(AE)/(AC)=(DE)/(BC)。

- 应用：在很多几何证明和计算中，若已知平行关系和部分线段长度，可以利用此模型求出其他线段的长度。

例如，已知AD = 2，AB = 5，BC = 6，求DE的长度。

根据(DE)/(BC)=(AD)/(AB)，可得DE=(AD× BC)/(AB)=(2×6)/(5)=(12)/(5)。

2. 8字模型。

- 基本图形：若有四边形ABDC，其中AB与CD相交于点E，则三角形AEC相似于三角形BED。

- 性质：(AE)/(BE)=(CE)/(DE)，并且AE× DE = BE× CE。

- 应用：在求解线段比例关系或者证明线段乘积相等时经常用到。

比如在一个几何图形中，已知AE = 3，BE = 4，CE = 6，求DE的长度。

根据AE× DE = BE×CE，可得DE=(BE× CE)/(AE)=(4×6)/(3)=8。

3. 母子相似三角形模型（射影定理模型）- 基本图形：在直角三角形ABC中，∠ ACB = 90^∘，CD垂直于AB于点D。

则三角形ACD相似于三角形ABC，三角形BCD相似于三角形BAC，三角形ACD相似于三角形CBD。

- 性质：- 在三角形ACD与三角形ABC中，AC^2=AD× AB。

- 在三角形BCD与三角形BAC中，BC^2=BD× AB。

- 在三角形ACD与三角形CBD中，CD^2=AD× BD。

- 应用：在涉及直角三角形中的线段长度计算和比例关系证明时非常有用。

例如，在直角三角形ABC中，∠ ACB = 90^∘，CD垂直于AB，AD = 2，DB = 8，求AC 的长度。

A BC DEAC DBEABCDDABDEFGD AB CEADCBECNOMDAEC BAEFBOEABCDA1.EC FC⇒⊥正方形ABCD中，BD⊥CE⇔BD＝CE平移后也成立2. //AB CDB D E⇒∠+∠=∠6.△ABD，△ACE为等边△⇒BE＝CDBE、CD相交所成锐角为60°//360AB CDB D E⇒∠+∠+∠=︒ABDE与ACFG为正方形⇒EC＝BG，BG⊥CE注：条件可换成△BAE，△CAG为等腰Rt△3.B D⇒∠=∠7.①AD平分∠CAB；②DE//AC；③AE＝DE中，知二推一1902BOCA⇒∠=︒+∠8. △ABC为等腰Rt△,AE平分∠CAB，∠D＝90︒⇒AE＝2BD12BOC A⇒∠=∠DE//BC⇒C△ADE＝AB+AC1902BOCA⇒∠=︒-∠9.AC＝BC，则CE⊥BD⇔CE＝BD△ACD、△BCE为等边△，A、C、B共线⇒△ACE≌△DCB; △ACM≌△DCN △MCE≌△NCB; AE＝BD，AM＝DN，EM＝BN，CM＝CN，AE、BD相交成锐角60°，AO＝DO+CO，BO＝EO+CO，OM+ON＝CO，OC平分∠AOB，注：△BCE绕C旋转时，结论有些变化.10. AC＝BC⇒△DEF为等腰Rt△15. ⇒OD＝OEBE+CD＝BCA ABCD21D CBAE FE F A ′B ′C′O ABCDAD BCEFE FMA C DB F MGAB C DE45︒FEABCD ⇒PB+PC ＝2PD ∠ABP+∠C ＝180°16.AD ＝CD ⇔CD ＝BD ⇔AD ＝BDAB ＝AC⇒AE+BE ＝BC17.⇒∠A ＝∠B或∠A+∠B ＝180°12.AC ＝BC⇒∠ADC ＝∠BDF ； CF+DF ＝AD18. ⇒DE+BF ＝EFAE 平分∠DEF ，AF 平分∠BFE13.⇒CD ＝CE ＝BG CEFD 为菱形∠2＝2∠1 ⇒AF ＝BC+CF14.AB ＝AC⇒DE+DF ＝BM （钝角△也成立）⇒AE+CF ＝CDEF OES 四边形OEBF ＝14a 2等腰梯形 ⇒EF+EG ＝CM⇒BE+DF=AEEFDCBAGHA B CDE FE B A CDABCNM DF AB CE H 1ADBCB ACDEFEC BADAB CDFEA BCDEFABCDEFA 19.BF=AD ⇔BF ⊥AD⇒∠1＝∠B△ADC ∽△CDB ∽△ACB AC 2=AD ·AB BC 2＝BD ·BAAC ·BC ＝AB ·CD CD 2＝AD ·BD BF=AC ⇔BF ⊥AC25.∠C ＝∠D⇔△ABC ∽△ADE ⇔AB ·AD ＝AC ·AE 20.中点四边形EFGH 至少是，取决于AC 、BD 的关系，EF ，EH 的关系对应AC 、BD 的关系26.∠B ＝∠E⇔△ADE ∽△ACB ⇔AD ·AB ＝AC ·AE21. 梯形ABCD 中： ①AE ＝BE ； ②AD+BC ＝CD ；③DE ⊥CE ，知二推一27.⇒DF ＝EF22. ⇒AM 2+BN 2＝MN 228.2AE AFED BF⇒=23.AD ＝BC ＝a ，BF ＝CF⇒HF+HD ＝a29. ⇒EF//ADEF ＝12(BC －AD)OMDCB AE N OFABCDENMOD C B A N A B C D EM aaM ABODE MEA CN B D FEB C D A1D CBA G E ABCDM FA24.∠1＝∠C⇔△ADE ∽△ACB ⇔AD ·AB ＝AE ·AC 30.⇒AN DGAM BC=∠1＝∠B⇔△ADC ∽△ACB ⇔∠ADC ＝∠ACB ⇔AC 2=AD ·AB31.DE//BC⇒DN ＝EN ， BM ＝CM35.⇒AO ＝2DO BO ＝2EO CO ＝2FO⇒MO ＝NO112AD BC MN +=⇒AB BM BNAC CM CN==32.⇒DM BN EM CN = 当DM ＝EM 时， 则BN ＝CN37.⇒222OD DE a += 222OD DE a +=同上33.⇒111AB CD EF+=34.AD ＝DC ，PN//BD ⇒PN+MN ＝2BDP FAB CDE MAO BCPAB ＝AC⇒PE+PF ＝2AD1半弧所对的圆心角等于整弧所对的圆心角 AOC APB ⇒∠=∠2（1）五元素：①CD 过圆心O ；②CD ⊥AB ；③AM ＝BM ；④AD BD ＝；⑤AC BC ＝中，知二推三。

几何图形的基本模型【典型例题】模型一：双子型（手拉手模型）——全等（1）等边三角形条件：ΔOAB, ΔOCD均为等边三角形。

结论：①ΔOAC≌ΔOBD ②AC=BD ③∠AEB=600④OE平分∠AED ⑤点E在ΔOAB的外接圆上（2）等腰直角三角形条件：ΔOAB, ΔOC D均为等腰直角三角形。

结论：①ΔOAC≌ΔOBD ②AC=BD ③∠AEB=900 ④OE平分∠AED ⑤点E在ΔOAB的外接圆上（3）任意等腰三角形条件：ΔOAB, ΔOCD均为等腰三角形。

结论：①ΔOAC≌ΔOBD ②AC=BD ③∠AEB=∠A0B ④OE平分∠AED（或∠AED的外角）⑤点E在ΔOAB的外接圆上例题：（1）如图①，△ABC中，AB=AC,在△ABC的外侧分别以AB,AC为腰作了两个等腰三角形ABD,ACE，分别取BD,CE,BC的中点M、N、G，连接GM、GN，线段GM与GN数量关系是；位置关系是（2）如图②，把等腰三角形ABC换为一般的锐角三角形，AB﹥AC,其中，其它条件不变，上述结论还成立吗？请说明理由。

（3）如图③，在（2）的基础上，又作了进一步的探究，向△ABC的内侧分别作等腰直角三角形ABD、ACE，其它条件不变，试判断△GMN的形状，并给与证明。

模型二：双子型（手拉手模型）——相似（1）一般情况条件：CD ∥AB(ΔOCD ∽ΔOAB ),将ΔOCD 旋转至右图位置结论：右图中①ΔOCD ∽ΔOAB⇔ΔOAC ∽ΔOBD ②延长AC 交BD 于点E ，必有∠AEB=∠AOB ③点E 在ΔOAB 的外接圆上。

（2） 特殊情况条件：CD ∥AB (ΔOCD ∽ΔOAB ), ∠AOB=∠COD=900将ΔOCD 旋转至右图位置结论：右图中①ΔOCD ∽ΔOAB ⇔ΔOAC ∽ΔOBD ②延长AC 交BD 于点E ，必有∠AEB=900（BD ⊥AC ）③连接AD,BC ,则S ABCD =12AC ×BD ④OD OC =OBOA =tan ∠OCD ⑤点E 在ΔOAB 的外接圆上(A,O,E,B 四点共圆) ⑥必有AD 2+BC 2=AB 2+CD 2例题：以平面上一点O 为直角顶点，分别画出两个直角三角形，记作△AOB 和△COD ，其中∠ABO=∠DCO=300(1)点E 、F 、M 分别是AC 、CD 、DB 的中点，连接FM 、EM. ① 如图1，当点D 、C 分别在AO 、BO 的延长线上时，FMEM =② 如图2，将图1中△AOB 的绕点O 沿顺时针方向旋转α角(00＜α＜600)，其他条件不变，判断FM EM的值是否发生变化，并对你的结论进行证明（3） 如图3，若B0=3√3，点N 在线段OD 上，且NO=2.点P 是线段AB 上的一个动点，在将ΔOAB 绕点0旋转过程中，线段PN 长度的最小值为 ，最大值为 。

⎧⎨⎩⎧⎨⎩人教版七年级数学上册第四章《几何图形初步》知识点汇总一、知识结构框图二、具体知识点梳理（一）几何图形(是多姿多彩的)立体图形：棱柱、棱锥、圆柱、圆锥、球等.1、几何图形平面图形：三角形、四边形、圆等.主（正）视图---------从正面看；2、几何体的三视图 侧（左）视图-----从左面边看；俯视图---------------从上面看.（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图.（2）能根据三视图描述基本几何体或实物原型.3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平面图形不一样的.（2）了解直棱柱、圆柱、圆锥的平面展开图，能根据展开图判断和制作立体模型.4、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形.线：面和面相交的地方是线，分为直线和曲线.面：包围着体的是面，分为平面和曲面.体：几何体也简称体.（2）点动成线，线动成面，面动成体.（二）直线、射线、线段1、基本概念图形直线射线线段端点个数无一个两个表示法直线a直线AB（BA）射线AB线段a线段AB（BA）作法叙述作直线AB作直线a 作射线AB作线段a作线段AB、连接AB延长叙述不能延长反向延长射线AB延长线段AB反向延长线段BA 2、直线的性质经过两点有一条直线，并且只有一条直线. 简称：两点确定一条直线.3、画一条线段等于已知线段（1）度量法（2）用尺规作图法4、线段的大小比较方法（1）度量法（2）叠合法5、线段的中点（二等分点）、三等分点、四等分点等定义：把一条线段平均分成两条相等线段的点叫做线段的中点.图形：A M B符号：若点M 是线段AB 的中点，则AM=BM=AB ，AB=2AM=2BM.126、线段的性质：两点的所有连线中，线段最短.简称：两点之间，线段最短.7、两点的距离：连接两点的线段长度叫做这两点的距离.8、点与直线的位置关系 （1）点在直线上； （2）点在直线外.（三）角1、角：由公共端点的两条射线所组成的图形叫做角.2、角的表示法（四种）：∠1 ； ； ； .α∠β∠ABC ∠3、角的度量单位及换算4、角的分类：锐角、直角、钝角、平角、周角.5、角的比较方法 （1）度量法 （2）叠合法6、角的和、差、倍、分及其近似值7、画一个角等于已知角（1）借助三角尺能画出15°的倍数的角，在0～180°之间共能画出11个角.（2）借助量角器能画出给定度数的角.（3）用尺规作图法，可以作出任意给定的角.8、角的平线线定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做角的平分线.图形： 符号：9、互余、互补（1）若∠1+∠2=90°，则∠1与∠2互为余角.其中∠1是∠2的余角，∠2是∠1的余角.（2）若∠1+∠2=180°，则∠1与∠2互为补角.其中∠1是∠2的补角，∠2是∠1的补角.（3）余（补）角的性质：同（等）角的余角相等. 同（等）角的补角相等.10、方向角（1）正方向；（2）北（南）偏东（西）方向；（3）东（西）北（南）方向.。

⎧⎨⎩⎧⎨⎩人教版七年级数学上册第四章《几何图形初步》知识点汇总一、知识结构框图二、具体知识点梳理（一）几何图形(是多姿多彩的)立体图形：棱柱、棱锥、圆柱、圆锥、球等. 1、几何图形 平面图形：三角形、四边形、圆等.主（正）视图---------从正面看； 2、几何体的三视图 侧（左）视图-----从左面边看；俯视图---------------从上面看.（1）会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图.（2）能根据三视图描述基本几何体或实物原型.3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平面图形不一样的.（2）了解直棱柱、圆柱、圆锥的平面展开图，能根据展开图判断和制作立体模型.4、点、线、面、体（1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形.线：面和面相交的地方是线，分为直线和曲线.面：包围着体的是面，分为平面和曲面.体：几何体也简称体.（2）点动成线，线动成面，面动成体.（二）直线、射线、线段1、基本概念2、直线的性质经过两点有一条直线，并且只有一条直线. 简称：两点确定一条直线.3、画一条线段等于已知线段（1）度量法（2）用尺规作图法4、线段的大小比较方法（1）度量法（2）叠合法5、线段的中点（二等分点）、三等分点、四等分点等定义：把一条线段平均分成两条相等线段的点叫做线段的中点.图形：A M B符号：若点M 是线段AB 的中点，则AM=BM=12AB ，AB=2AM=2BM. 6、线段的性质：两点的所有连线中，线段最短.简称：两点之间，线段最短.7、两点的距离：连接两点的线段长度叫做这两点的距离.8、点与直线的位置关系 （1）点在直线上； （2）点在直线外.（三）角1、角：由公共端点的两条射线所组成的图形叫做角.2、角的表示法（四种）：∠1 ； α∠ ； β∠ ； ABC ∠.3、角的度量单位及换算4、角的分类：锐角、直角、钝角、平角、周角.5、角的比较方法 （1）度量法 （2）叠合法6、角的和、差、倍、分及其近似值7、画一个角等于已知角（1）借助三角尺能画出15°的倍数的角，在0～180°之间共能画出11个角.（2）借助量角器能画出给定度数的角.（3）用尺规作图法，可以作出任意给定的角.8、角的平线线定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做角的平分线. 图形： 符号：9、互余、互补（1）若∠1+∠2=90°，则∠1与∠2互为余角.其中∠1是∠2的余角，∠2是∠1的余角.（2）若∠1+∠2=180°，则∠1与∠2互为补角.其中∠1是∠2的补角，∠2是∠1的补角.（3）余（补）角的性质：同（等）角的余角相等. 同（等）角的补角相等.10、方向角（1）正方向；（2）北（南）偏东（西）方向；（3）东（西）北（南）方向.。