复试材料力学重点知识点总结(二轮主要).pptx
- 格式:pptx
- 大小:341.13 KB
- 文档页数:30

材料力学知识点归纳总结(完整版)1.材料力学:研究构件(杆件)在外力作用下内力、变形、以及破坏或失效一般规律的科学,为合理设计构件提供有关强度、刚度、稳定性等分析的基本理论和方法。
2.理论力学:研究物体(刚体)受力和机械运动一般规律的科学。
3.构件的承载能力:为保证构件正常工作,构件应具有足够的能力负担所承受的载荷。
构4.件应当满足以下要求:强度要求、刚度要求、稳定性要求5.变形固体的基本假设:材料力学所研究的构件,由各种材料所制成,材料的物质结构和性质虽然各不相同,但都为固体。
任何固体在外力作用下都会发生形状和尺寸的改变——即变形。
因此,这些材料统称为变形固体。
第二章:内力、截面法和应力概念1.内力的概念:材料力学的研究对象是构件,对于所取的研究对象来说,周围的其他物体作用于其上的力均为外力,这些外力包括荷载、约束力、重力等。
按照外力作用方式的不同,外力又可分为分布力和集中力。
2.截面法:截面法是材料力学中求内力的基本方法,是已知构件外力确定内力的普遍方法。
已知杆件在外力作用下处于平衡,求m-m截面上的内力,即求m-m截面左、右两部分的相互作用力。
首先假想地用一截面m-m截面处把杆件裁成两部分,然后取任一部分为研究对象,另一部分对它的作用力,即为m-m截面上的内力N。
因为整个杆件是平衡的,所以每一部分也都平衡,那么,m-m截面上的内力必和相应部分上的外力平衡。
由平衡条件就可以确定内力。
例如在左段杆上由平衡方程N-F=0 可得N=F3.综上所述,截面法可归纳为以下三个步骤:1、假想截开在需求内力的截面处,假想用一截面把构件截成两部分。
2、任意留取任取一部分为究研对象,将弃去部分对留下部分的作用以截面上的内力N来代替。
3、平衡求力对留下部分建立平衡方程,求解内力。
4.应力的概念:用截面法确定的内力,是截面上分布内力系的合成结果,它没有表明该分布力系的分布规律,所以,为了研究相伴的强度,仅仅知道内力是不够的。

材料力学各章重点内容总结第一章 绪论一、材料力学中工程构件应满足的3方面要求是:强度要求、刚度要求和稳定性要求。
二、强度要求是指构件应有足够的抵抗破坏的能力;刚度要求是指构件应有足够的抵抗变形的能力;稳定性要求是指构件应有足够的保持原有平衡形态的能力。
三、材料力学中对可变形固体进行的3个的基本假设是:连续性假设、均匀性假设和各向同性假设。
第二章 轴向拉压一、轴力图:注意要标明轴力的大小、单位和正负号。
二、轴力正负号的规定:拉伸时的轴力为正,压缩时的轴力为负。
注意此规定只适用于轴力,轴力是内力,不适用于外力。
三、轴向拉压时横截面上正应力的计算公式:N F Aσ= 注意正应力有正负号,拉伸时的正应力为正,压缩时的正应力为负。
四、斜截面上的正应力及切应力的计算公式:2cos ασσα=,sin 22αστα=注意角度α是指斜截面与横截面的夹角。
五、轴向拉压时横截面上正应力的强度条件[],maxmax N F A σσ=≤六、利用正应力强度条件可解决的三种问题:1.强度校核[],maxmax N F A σσ=≤一定要有结论 2.设计截面[],maxN F A σ≥ 3.确定许可荷载[],max N F A σ≤七、线应变l l ε∆=没有量纲、泊松比'εμε=没有量纲且只与材料有关、 胡克定律的两种表达形式:E σε=,N F l l EA∆= 注意当杆件伸长时l ∆为正,缩短时l ∆为负。
八、低碳钢的轴向拉伸实验:会画过程的应力-应变曲线,知道四个阶段及相应的四个极限应力:弹性阶段(比例极限p σ,弹性极限e σ)、屈服阶段(屈服极限s σ)、强化阶段(强度极限b σ)和局部变形阶段。
会画低碳钢轴向压缩、铸铁轴向拉伸和压缩时的应力-应变曲线。
九、衡量材料塑性的两个指标:伸长率1100l l lδ-︒=⨯︒及断面收缩率1100A A Aϕ-︒=⨯︒,工程上把5δ︒≥︒的材料称为塑性材料。
十、卸载定律及冷作硬化:课本第23页。




“材料力学”重点归纳
第一章静力学基础
掌握:静力学基本概念和定理:力、力偶、平衡力系、等效力系、合力投影定理、合力矩定理、力线平移定理、静力学的基本任务等。
重点掌握:掌握各种力系的简化和平衡方程应用。
了解材料力学的发展沿革,理解本课程的任务、内容、目的。
第二章材料力学绪论
掌握:了解材料力学的基本任务和杆件的基本变形。
重点掌握:材料力学的基本概念:弹性变形、塑性变形、破坏、强度、刚度、稳定性、内力、应力、应变等。
第三章应力分析和应变分析理论
掌握:应力状态、应力张量、应力张量不变量、空间应力圆、等效应力、八面体应力、变形位移、应变状态、应变张量、偏斜应力张量、偏斜应变张量等概念。
应力分析理论、应变分析理论。
重点掌握:应力状态、应力张量、应力张量不变量、空间应力圆、等效应力、八面体应力、变形位移、应变状态、应力分析理论。
第四章固体材料的弹性本构关系和塑性本构关系
掌握:固体材料弹性变形和塑性变形的主要特点、弹性本构关系(广义胡克定律)、主应力空间、屈服函数、常用屈服条件、常用强度理论等。
重点掌握:固体材料弹性变形和塑性变形的主要特点、弹性本构关系(广义胡克定律)、常用屈服条件和强度理论等。
第五章材料力学实验
了解和掌握金属材料单轴拉伸和压缩力学实验的原理和方法。
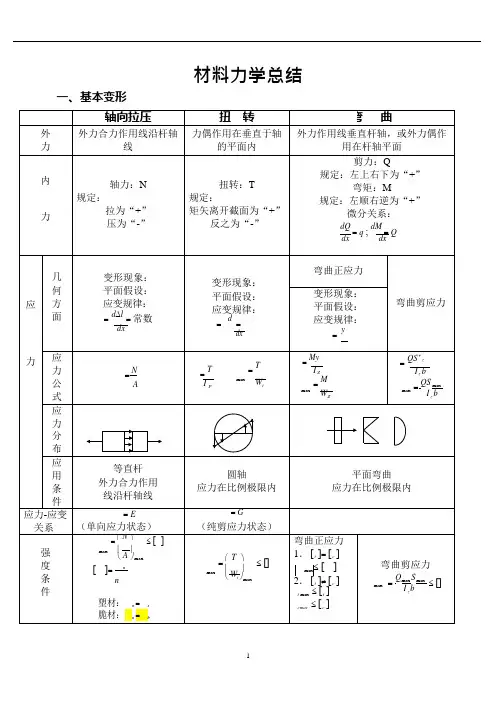
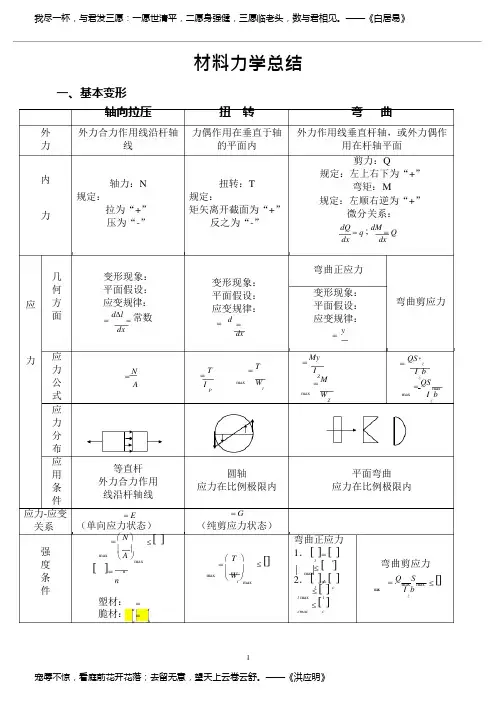
一、基本变形材料力学总结变形现象: 平面假设: 应变规律: = d ∆l = 常数dx变形现象:平面假设: 应变规律:=d = dx变形现象:平面假设: 应变规律:= y= N =T= T = MyI Z = M max WZ= QS * z I z b = QS max max I bz max W= E (单向应力状态) = G(纯剪应力状态)=⎛ N ⎫≤ []maxA ⎪ ⎝ ⎭max[]=un塑材:u=s 脆材:u =bmax= ⎛ T ⎫ ≤ [] ⎪ ⎝ W t ⎭max弯曲正应力 1. [t ]= [c ]max≤ []2. [t ]≠ [c ] t max ≤ [t ] cmac ≤ [c ]弯曲剪应力=Q max S max ≤ [] max I bz轴向拉压扭转弯曲刚度条=T ⋅180 ≤[]max GIP注意:单位统一ymax≤[y]max≤[]件变形d∆l=N ; ∆L =NLdx EA EAEA—抗拉压刚度=d=Tdx GIZ=TLGIPGI p—抗扭刚度1=M (x)(x) EIy '' =M (x)EIEI—抗弯刚度应用条件应力在比例极限圆截面杆,应力在比例极限小变形,应力在比例极限矩形A=bhbh 3bh 2IZ=12;WZ=6实心圆A= d 24d4d3IP=32;Wt=16d4d3IZ=64;WZ=32空心圆D 2A =(1-2)4d44IP=32(1 -)d 3W =(1 -4)t16d 4I =(1-4)Z64d34WZ=32(1-)其(1)'剪切(1)强度条件:=Q≤[]A—剪切面积A(2)挤压条件:=P bs ≤[]bs A bsJA j—挤压面积矩形:=3Qmax 2 A圆形:=4Qmax 3A环形:= 2Qmax Amax均发生在中性轴上它公(2)GE式2(1 )二、还有:(1)外力偶矩:m = 9549 N (N •m)n(2)薄壁圆管扭转剪应力:=TN—千瓦;n—转/分2r 2t(3)矩形截面杆扭转剪应力:max =Tb2h;=TG b3hDB c AD 'Z ZC c cn n三、截面几何性质(1)平行移轴公式:I =I +a 2A;(2)组合截面:IYZ=IZ Y+abA1.形心:y c∑A i y ci=i =1 ;∑A ii =1∑A i z ciz =i =1∑A ii =12.静矩:S Z =∑A i y ci ;S y =∑A i z ci3.惯性矩:I Z =∑(I Z ) i ;I y =∑(I y ) i四、应力分析:(1)二向应力状态(解析法、图解法)a.解析法: b.应力圆:n σ:拉为“+”,压为“-”xτ:使单元体顺时针转动为“+”x yx y cos 2sin 2α:从x 轴逆时针转到截面的法线为“+”2 2 xx y sin 2cos 22 xtg22xmaxminxx yy2c:适用条件:平衡状态(2)三向应力圆:;; 1 3max 1 min 3 max 2nn2x y22xyxc121223311(3) 广义虎克定律:1(1 (1E 123xE xyz1 ( 1(2E 231yE yzx1(1(3E3 1 2zExy*适用条件:各向同性材料;材料服从虎克定律(4) 常用的二向应力状态 31. 纯剪切应力状态:1,20 ,3x2. 一种常见的二向应力状态:132r 3r 4五、强度理论破坏形式脆性断裂塑性断裂强度理论 第一强度理论(最大拉应力理论)莫尔强度理论 第三强度理论 (最大剪应力理论) 第四强度理论(形状改变比能理论) 破坏主要因素 单元体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件 1 = bmax =su f = u fs强度条件 1 ≤ [] 1-3≤ []适用条件 脆性材料 脆性材料 塑性材料 塑性材料*相当应力:r,,]r 11r 313r 4222242232r=2+42≤[]=2+32≤[]4r22(M +N ) + 4≤ []r3 =r=(M+N)2+32≤[]WM 2 +T 2r3 =圆截面WM 2 + 0.75T 2r4=(M+N)2 + 4(T)2W Z A W t(M+N)2 + 4(T)2W Z A W t α 中性轴ZMpr3 =≤ []r 4 =≤ []i 2I Z*y =-=-ZAe y e ytg=y=-I ZtgZ I y中性轴Z≤ []Z≤ []A W≤ []P Mmax =±max ±max≤ []sincos( +)W Z W y=max maxM强度条件43=±P ±MA W)I yI Z=M (y c os+z s in公式简图弯扭拉(压)弯扭拉(压)弯斜弯曲类型六、材料的力学性质脆性材料<5%塑性材料≥5%低碳钢四阶段:(1)弹性阶段(2)屈服阶段(3)强化阶段(4)局部收缩阶段b强度指标s ,b e sα塑性指标,tg E七.组合变形只有σs,无σbb剪断断口垂直轴线拉断断口与轴夹角45ºb45º拉断铸铁断口垂直轴线剪断s b 滑移线与轴线45︒,剪45低碳钢扭压拉八、压杆稳定欧拉公式: P=2EI min,=2E,应用范围:线弹性范围,σ<σ ,λ>λcr(l ) 2cr2crpp柔度:=ul;=E;0 =a -s, σib柔度是一个与杆件长度、约束、截面尺寸、形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:cr =2E2临界应力λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σsλoλPλ稳定校核:安全系数法: n P c rP I n w ,折减系数法:P []A提高杆件稳定性的措施有: 1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。


第一章 绪 论一、基本要求(1)了解构件强度、刚度和稳定性的概念,明确材料力学课程的主要任务。
(2)理解变形固体的基本假设、条件及其意义。
(3)明确内力的概念、初步掌握用截面法计算内力的方法。
(4)建立正应力、剪应力、线应变、角应变及单元体的基本概念。
(5)了解杆件变形的受力和变形特点。
二、重点与难点1.外力与内力的概念外力是指施加到构件上的外部载荷(包括支座反力)。
在外力作用下,构件内部两部分间的附加相互作用力称为内力。
内力是成对出现的,大小相等,方向相反,分别作用在构件的两部分上,只有把构件剖开,内力才“暴露”出来。
2.应力,正应力和剪应力在外力作用下,根据连续性假设,构件上任一截面的内力是连续分布的。
截面上任一点内力的密集程度(内力集度),称为该点的应力,用p 表示0lim A P dP p A dA→∆==∆ P ∆为微面积A ∆上的全内力。
一点处的全应力可以分解为两个应力分量。
垂直于截面的分量称为正应力,用符号σ表示;和截面相切的分量称为剪应力,用符号τ表示。
应力单位为Pa 。
1MPa=610Pa, 1GPa=910Pa 。
应力的量纲和压强的量纲相同,但是二者的物理概念不同,压强是单位面积上的外力,而应力是单位面积的内力。
3.截面法截面法是求内力的基本方法,它贯穿于“材料力学”课程的始终。
利用截面法求内力的四字口诀为:切、抛、代、平。
一切:在欲求内力的截面处,假想把构件切为两部分。
二抛:抛去一部分,留下一部分作为研究对象。
至于抛去哪一部分,视计算的简便与否而定。
三代:用内力代替抛去部分队保留部分的作用力。
一般地说,在空间问题中,内力有六个分量,合力的作用点为截面形心。
四平:原来结构在外力作用下处于平衡,则研究的保留部分在外力与内力共同作用也应平衡,可建立平衡方程,由已知外力求出各内力分量。
4.小变形条件在解决材料力学问题时的应用由于大多数材料在受力后变形比较小,即变形的数量远小于构件的原始尺寸。