实验三 转速负反馈闭环调速系统的仿真

计算机仿真技术作业一——转速反馈单闭环直流调速系统仿真*名：***班级：电气1102学号： ********日期： 2014年5月4日指导老师：***北京交通大学计算机仿真技术作业一题目：转速反馈单闭环直流调速系统仿真直流电机模型框图如下图所示，仿真参数为R=0.6Ω，T l=0.00833，T m=0.045，Ce=0.2。

本次仿真采用算法为ode45，仿真时间5s。

图1 直流电机模型1、开环仿真：用simulink实现上述直流电机模型，直流电压U d0取220V，time n 转速times静差率仿真算法为ode230.511.522.533.544.55time n 转速times静差率选择仿真算法ode23时，在2.5s 之后转速发生小幅度震荡，后来趋于稳定,运算时间和精度相差不大 2、闭环仿真：在上述仿真基础上，添加转速闭环控制器，转速指令为1130rpm ，0~2.5s ，电机空载，即I d =0；比例环节：Kp=4 2.5s~5s ，电机满载，即I d =55A 。

比例环节：Kp=4(1)控制器为比例环节：试取不同k p 值，画出转速波形，求稳态时n 和s 并进行比较。

在Simulink 中建立系统模型如下图所示time times静差率Kp=1Kp=2时转速n 稳态值为5784rpm ，静差率s 稳态值为-4.0609time ntimes静差率Kp=2Kp=4时转速n 稳态值为5827rpm ，静差率s 稳态值为-4.0982time n转速Kp=4times静差率Kp=4Kp=5时转速n 稳态值为5835rpm ，静差率s 稳态值为-4.1054time ntimes静差率Kp=5记录数据如下表所示结论:由图像可得，Kp 越大，转速n 超调量越大(2)控制器为比例积分环节，设计恰当的k p 和k I 值，并与其它不同的k p 和k I 值比较，画出不同控制参数下的转速波形，比较静差率、超调量、响应时间和抗扰性。

黑龙江科技大学电气与控制工程学院M a tｌa b考试论文题目带转速负反馈的有静差直流调速系统仿真专业自动化姓名班级学号２０13年12 月 03日带转速负反馈的有静差直流调速系统仿真摘要:为了提高直流调速系统的动态、静态性能，通常采用闭环控制系统（主要包括单闭环、双闭环）。

而在对调速指标要求不高的场合,采用单闭环即可。

闭环系统较之开环系统能自动侦测把输出信号的一部分拉回到输入端,与输入信号相比较，其差值作为实际的输入信号;能自动调节输入量，能提高系统稳定性。

在对调速系统性能有较高要求的领域常利用直流电动机,但直流电动机开环系统稳定性不能够满足要求，可利用转速单闭环提高稳态精度,而采用比例调节器的负反馈调速系统仍是有静差的，为了消除系统静差，可采用积分调节器代替比例调节器。

MAＴＬＡB仿真在科学研究中的地位越来越高，本文就简单的带转速负反馈的有静差直流调速系统这个例子,通过对MＡTLＡB的仿真,改变Ｕn*、Kｐ得到不同的仿真结果。

通过对仿真结果的对比,从而总结出如何在仿真过程中对MATLAB的仿真做到最优选择。

关键词：直流调速单闭环稳态精度比例调节MATLAB仿真1引言直流调速是现代电力拖动自动控制系统中发展较早的技术。

在20世纪６0年代,随着晶闸管的出现，现代电力电子和控制理论、计算机的结合促进了电力传动控制技术研究和应用的繁荣。

晶闸管-直流电动机调速系统为现代工业提供了高效、高性能的动力。

尽管目前交流调速的迅速发展,交流调速技术越趋成熟，以及交流电动机的经济性和易维护性，使交流调速广泛受到用户的欢迎。

但是直流电动机调速系统以其优良的调速性能仍有广阔的市场,并且建立在反馈控制理论基础上的直流调速原理也是交流调速控制的基础。

现在的直流和交流调速装置都是数字化的，使用的芯片和软件各有特点,但基本控制原理有其共性。

长期以来，仿真领域的研究重点是仿真模型的建立这一环节上，即在系统模型建立以后要设计一种算法。

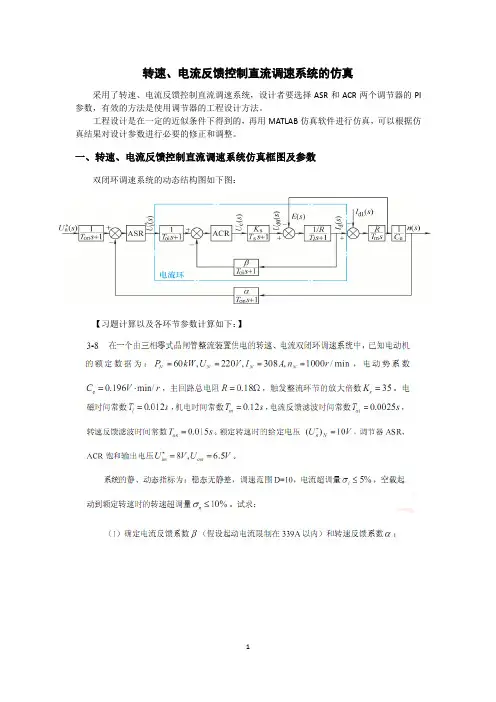
运动控制系统仿真实验报告——转速、电流反馈控制直流调速系统的仿真双闭环直流调速系统仿真对例题3.8设计的双闭环系统进行设计和仿真分析,仿真时间10s 。

具体要求如下： 在一个由三相零式晶闸管供电的转速、电流双闭环调速系统中，已知电动机的额定数据为：60=N P kW , 220=N U V , 308=N I A , 1000=N n r/min , 电动势系数e C =0.196 V·min/r , 主回路总电阻R =0.18Ω,变换器的放大倍数s K =35。

电磁时间常数l T =0.012s,机电时间常数m T =0.12s,电流反馈滤波时间常数i T 0=0.0025s,转速反馈滤波时间常数n T 0=0.015s 。

额定转速时的给定电压(U n *)N =10V,调节器ASR ，ACR 饱和输出电压U im *=8V,U cm =7.2V 。

系统的静、动态指标为:稳态无静差,调速范围D=10,电流超调量i σ≤5% ,空载起动到额定转速时的转速超调量n σ≤10%。

试求：（1）确定电流反馈系数β(假设起动电流限制在1.3N I 以内)和转速反馈系数α。

（2）试设计电流调节器ACR.和转速调节器ASR 。

（3）在matlab/simulink 仿真平台下搭建系统仿真模型。

给出空载起动到额定转速过程中转速调节器积分部分不限幅与限幅时的仿真波形（包括转速、电流、转速调节器输出、转速调节器积分部分输出），指出空载起动时转速波形的区别，并分析原因。

（4）计算电动机带40%额定负载起动到最低转速时的转速超调量σn 。

并与仿真结果进行对比分析。

（5）估算空载起动到额定转速的时间，并与仿真结果进行对比分析。

（6）在5s 突加40%额定负载，给出转速调节器限幅后的仿真波形（包括转速、电流、转速调节器输出、转速调节器积分部分输出），并对波形变化加以分析。

（一）实验参数某晶闸管供电的双闭环直流调速系统，整流装置采用三相桥式电路，基本数据如下： • 直流电动机：220V ，136A ，1460r/min ，C e=0.132Vmin/r ，允许过载倍数λ=1.5； • 晶闸管装置放大系数：K s=40； • 电枢回路总电阻：R =0.5Ω ； • 时间常数：T i=0.03s ， T m=0.18s ；• 电流反馈系数：β=0.05V/A （≈10V/1.5I N ）。

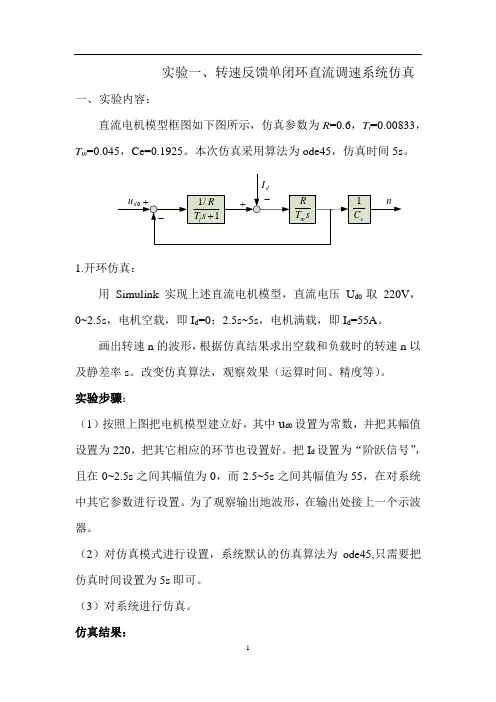
实验一、转速反馈单闭环直流调速系统仿真一、实验内容：直流电机模型框图如下图所示，仿真参数为R=0.6，T l=0.00833，T m=0.045，Ce=0.1925。

本次仿真采用算法为ode45，仿真时间5s。

1.开环仿真：用Simulink实现上述直流电机模型，直流电压U d0取220V，0~2.5s，电机空载，即I d=0；2.5s~5s，电机满载，即I d=55A。

画出转速n的波形，根据仿真结果求出空载和负载时的转速n以及静差率s。

改变仿真算法，观察效果（运算时间、精度等）。

实验步骤：（1）按照上图把电机模型建立好，其中u d0设置为常数，并把其幅值设置为220，把其它相应的环节也设置好。

把I d设置为“阶跃信号”，且在0~2.5s之间其幅值为0，而2.5~5s之间其幅值为55，在对系统中其它参数进行设置。

为了观察输出地波形，在输出处接上一个示波器。

（2）对仿真模式进行设置，系统默认的仿真算法为ode45,只需要把仿真时间设置为5s即可。

（3）对系统进行仿真。

仿真结果：（1）仿真算法为ode45:图1 上图即为电机转速的仿真结果图，同图上我们可以看出来分为了两个阶段，其中第一个阶段（0~2.5s）为空载转速，第二阶段（2.5~5s）为满载转速。

空载转速为1142n/min。

在2.5s时加入了负载，通过仿真结果我们可以看出来，负载转速为972n/min。

这可以看出来在加入负载之后，电机的转速开始下降。

根据电机转差率的公式s=（n0-n）/ n0=(1142-972)/1142=0.149。

转差率还是比较小的，说明该电机效率比较高。

通过观察该仿真的时间，其运算时间为T=9.134*10^-7s。

（2）仿真算法为ode23:仿真结果图如图2所示，由图我们可以看出来，结果基本上和计算方法为ode45的结果一样，但是运算时间却不一样，该算法的运算时间为T=3.636*10^-7s。

运算时间比ode45的时间短。

带电流截止负反馈的转速单闭环直流调速系统设计与仿真 一、设计要求系统稳定并无静差 二、给定参数17,220,3000/min N N N P kw U V n r ===，I N =87.3A ，电枢回路电阻0.087a R =Ω，电感0.0032a L H =,励磁回路电阻181.5Ω,电动机的转动惯量20.76.J Kg m =三、闭环直流调速系统稳态参数的计算 1）额定负载时的稳态速降应为：m i n/12.6min /)02.01(1002.03000)1(r r s D s n n N cl =-⨯⨯≤-=∆2）闭环系统应有的开环放大系数：计算电动机的电动势系数： r V r V n R I U C N a N N e min/071.0min/3000087.03.87220⋅=⋅⨯-=-=闭环系统额定速降为：min /97.106min /071.0087.03.87r r C R I n e N op =⨯==∆闭环系统的开环放大系数为：5.16112.697.1061=-≥-∆∆=clop n n K003.0/max max n ==n U α3）计算运算放大器的放大系数和参数 运算放大器放大系数K p 为:5.16/e p ≥=s K KC K α电枢回路的总电感为0.0032H电磁时间常数为037.0/l ==R L T 27/1l ==τK4)电流截止负反馈 四加电网扰动（第8s电压220→240）负载扰动给定值扰动五、将PI调节器参数改变1.电网扰动（第8s电压220→240）2.负载扰动3.给定值扰动转速、电流双闭环直流调速系统设计与仿真一、设计要求系统稳定并无静差 二、给定参数17,220,3000/min N N N P kw U V n r ===，I N =87.3A ，电枢回路电阻0.087a R =Ω，电感0.0032a L H =,励磁回路电阻181.5Ω,电动机的转动惯量20.76.J Kg m =三、电流调节器ACR 参数计算允许电流过载倍数λ=2；设调节器输入输出电压im nm **U U ==10V ，电力电子开关频率为f=l kHz ．首先计算电流反馈系数β和转速反馈系数α：06.0 I n im *==ββλU N U n nm *α= α=0.003s T 001.0s = ，电流环小时间常数为s T T T oi 002.0s i =+=∑电流调节器超前时间常数为s T K l i 015.0/1i ===τ 而对电流环开环增益局l K =250/5.0=∑i T ，于是ACR 的比例系数为：94.4/i l i ==s K R K K βτ 四、转速调节器ASR 参数计算 选中频段宽度h=5。

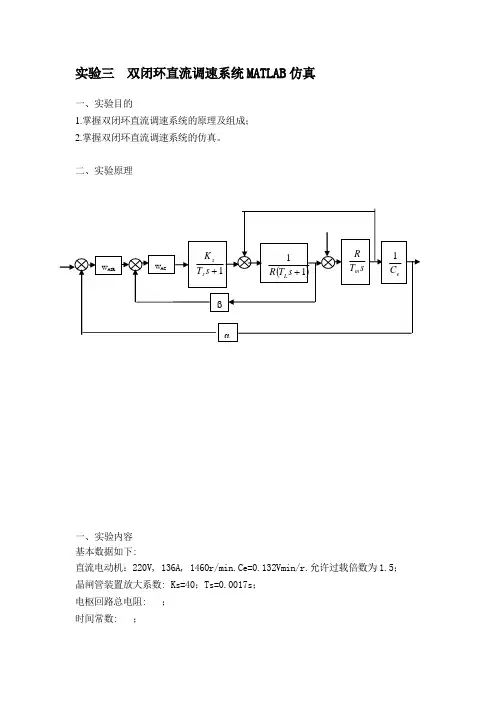
实验三双闭环直流调速系统MATLAB仿真
一、实验目的
1.掌握双闭环直流调速系统的原理及组成；
2.掌握双闭环直流调速系统的仿真。

二、实验原理
一、实验内容
基本数据如下:
直流电动机：220V, 136A, 1460r/min.Ce=0.132Vmin/r.允许过载倍数为1.5；晶闸管装置放大系数: Ks=40；Ts=0.0017s；
电枢回路总电阻: ；
时间常数: ；
电流反馈系数: ；
电流反馈滤波时间常数: ；
电流反馈系数: ；
转速反馈系数α=0.007vmin/r
转速反馈滤波时间常数:
设计要求：设计电流调节器, 要求电流无静差, 电流超调量。

转速无静差, 空载起动到额定负载转速时转速超调量。

并绘制双闭环调速系统的动态结构图。

四、实验步骤
1. 根据原理和内容搭建电路模型；
2. 设置各元器件的参数；
3. 设置仿真参数：仿真时间设为0.06s；计算方法为ode15或ode23。

4. 仿真实现。

五、实验报告
1.Idl=0和Idl=136A时电流和转速的输出波形
2.讨论PI 调节器参数对系统的影响.
τi =TL,s
i i K R
T KT Kp βτ•∑=
…………………………取KT=0.5 转速环设计成典型二型系统
h =5, T 087.0)2(=+==∑∑on i n n T T h hT τ Kn=7.112)1(=∑+=
n
RT h CeTm
h Kn αβ
取11.7 , 11.7/0.087。

邮局订阅号：82-946360元/年技术创新仿真技术《PLC 技术应用200例》您的论文得到两院院士关注转速负反馈闭环直流调速系统的分析与仿真Analysis and Simulate the Negative Feedback Loop DC Speed Control System(上海理工大学)孙凌杰左小五SUN Ling-jie ZUO Xiao-wu摘要:到目前为止,虽然在交流电动机的调速问题方面已经解决,但是在速度调节要求却较高,本文主要介绍转速闭环直流调速系统的工作原理,并在此基础上对转速闭环直流电动机的调速系统进行分析,借助MATLAB/SIMULINK 建立起仿真图并进行仿真与分析。

论文中给出了各个物理量的波形并对波形进行了分析从而对转速闭环调速系统的稳定性方面得出了一些结论。

该调速控制系统可以实现平滑的调速,且具有良好的动静态调速性能,仿真结果验证了系统设计的有效性、可行性。

关键词:转速闭环调速系统;直流电动机;仿真中图分类号:TM44文献标识码:AAbstract:So far,although the AC motor speed control problem has been solved,it requires a higher speed of adjustment,this article introduces the Principle of the speed closed-loop DC drive system,ana-lysis the speed closed-loop DC motor speed control system and set up the simulation chart on the matlab/simulink .Papers presented in the various physical and wave ,As well as an analysis of waveforms and thus get some conclutions on the stability aspect from the closed -loop speed con -trol system .The speed control system can achieve smooth speed control,and has a good dynamic and static speed performance,simulation results show the effec -tiveness of the system design and feasibility.Key words:speed closed-loop speed control system;DC Motors;Simulation文章编号:1008-0570(2010)10-1-0153-021引言能源问题日趋成人们争论的主题。