典型信号相关分析

第2章随机信号2.1 定义与基本特性2.2 典型信号举例2.3 一般特性与基本运算2.4 多维高斯分布与高斯信号2.5 独立信号2.2.1 随机正弦信号给定具有某种概率分布的振幅随机变量A 、角频率随机变量Ω与相位随机变量Θ，（具体概率分布与特性视应用而定），以（时间）参量t 建立随机变量于是，相应于某个参量域T 的随机变量族为正弦随机信号（或称为正弦随机过程)。

2.2 典型信号举例(,)sin()t W W t A t ξ==Ω+Θ{}T t W t ∈,§2.2各种样本函数集中显示的各种样本函数t ＝5时刻的不确定性1(1,); 1,,W A ξπ=Ω=2(1,); 1,,A ξπ=Ω=(1,); 1.5,2,/2n A ξππ=Ω=Θ=123(5,)(5,)(5,)W W W ξξξ举例正弦随机信号{W(t)=Acos(ωt+Θ), -∞<t<∞}其中，A服从参数为σ2的瑞利分布, 而Θ~u[0,2π], 并且A与Θ是独立的。

讨论随机信号W(t)的基本特性。

举例续解答：（1）均值20[()][cos()] [][cos()]1[]cos()2 0E W t E A t E A E t E A t d πωωωθθπ=+Θ=+Θ=⋅+⋅=∫1(,R t t [E =222121200212cos(2)cos()1122222cos ()t t t t d d t t ππωωθωωσθθππσω++−⎡⎤=⋅⋅+⋅⎢⎥⎣⎦=−∫∫21212 []cos(2)cos()/2E A E t t t t ωωωω=++Θ+−2σ∫一、二阶概率密度函数令111222(,)cos()(,)cos()X g A A t X g A A t ωω=Θ=+Θ⎧⎨=Θ=+Θ⎩22220(,)200a A a e a f a a σθπσ−Θ⎧≥⎪=⎨⎪<⎩1112212cos()sin()1cos()sin()sin ()t a t J t a t a t t ωθωθωθωθω−+−+==+−+−12221212012221212122cos ()2sin ()(,;,)(,)1X X X x x x x t t t t f x x t t f x x ωσω+−−−−=012cos ()t t ρω=−2.2.2 贝努里随机序列2.2.2 贝努里随机序列101举例问题：分析贝努里随机信号X(n)基本特性。

常见雷达信号分析研究摘要：雷达是探测目标和测定与目标距离的电子设备，在雷达使用过程中，需要对目标发出电磁波，并接收回波，由此来测定目标和其的空间方位等。

雷达信号是关乎雷达使用效果的基础，要根据无线电监测的实际需要，明确常见雷达信号分类，并了解常见雷达信号的重要参数，这样才能保证监测效果。

基于此，本文分析了雷达信号的主要特征，并就常见的雷达信号进行探究，仅供大家参考。

关键词：雷达信号；特征；分类引言：现代社会对雷达的应用十分广泛，如在军事领域的应用、气象监测中的应用等。

不同的应用领域对雷达信号也有着不同的要求，因此要做好雷达信号的分类，同时还要明确不同雷达信号的主要特征，掌握其关键参数，这样才能更好的为无线电监测工作服务。

因此针对常见雷达信号的分析研究具有十分重要的意义。

1雷达信号分类雷达信号的种类，一般按照其特性可把雷达信号分成两大类，即简单连续波雷达和脉冲雷达。

而针对前者来说，又可分成简单连续波雷达信号和调频连续波雷达信号两类，简单连续波雷达信号主要用作在于观测对象移动速率的测定，而调频连续波雷达信号则主要使用于目标距离测定。

连续波雷达信号的使用比较广泛，其应用量已达雷达信号的10%左右。

对后者来说，可分成简单的脉冲雷达信号、脉冲压缩雷达信号、频率捷变雷达信号和脉冲多普勒雷达信号三种形态。

不同的雷达信号有着不同的作用，以简单脉冲雷达信号为例，这种信号主要用于距离测试。

再以频率捷变雷达信号为例，这种信号主要由于提升雷达的抗干扰能力，可以更好的规避相关干扰因素，保障雷达信号的稳定性。

总之，雷达信号的类型多样，其分类比较复杂，只有明确雷达信号类型才能保证其应用效果。

2雷达信号关键参数分析雷达信号关键参数主要包括脉冲重复周期、脉冲重复频率、脉冲信号持续时间等，分别表示为(Tr)、(fr)、(τ)，其中，(τ) 是指发射脉冲的时间，而(fr) 则是指以秒为单位情况下，射频脉冲个数，(Tr) 则是指脉冲发射间隔的时间。

实验十一 典型信号的概率密度分析一. 实验目的在理论学习的基础上，通过本实验熟悉典型信号的概率密度函数特点，加深对概率密度函数分析的概念、性质、作用的理解，掌握用其分析信号幅值特性的方法。

二. 实验原理随机信号的概率密度函数定义为：p x x p x x t x x x ()lim(())=−→−∞<≤+∆∆∆ (1)它反映了信号落在不同幅值强度区域内的概率情况。

对于各态历经过程：p x x xT T Tx()lim[lim]=−→−−→−∞∆01(2)下图显示了一个样例信号x(t)的波形和p(x)的计算方法。

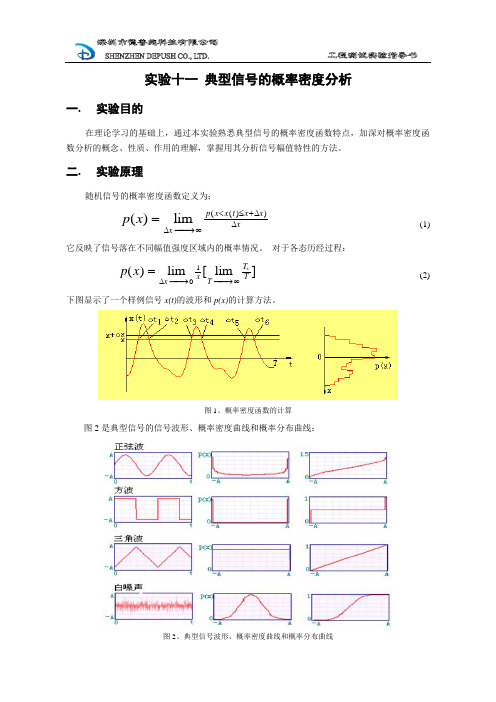
图1、概率密度函数的计算图2是典型信号的信号波形、概率密度曲线和概率分布曲线：图2、典型信号波形、概率密度曲线和概率分布曲线三. 实验内容概率密度函数给出了信号取不同幅值大小的概率，在随机振动、随机疲劳试验等应用场合，常常利用它来检测信号的正态性和了解信号的幅值大小分布情况。

实验内容为分析正弦波、方波、三角波和白噪声信号的概率密度函数。

四. 实验仪器和设备1. 计算机1台2. DRVI快速可重组虚拟仪器平台1套3. 打印机1台五. 实验步骤1.运行DRVI主程序，点击DRVI快捷工具条上的"联机注册"图标，选择其中的“DRVI采集仪主卡检测”或“网络在线注册”进行软件注册。

2.在DRVI软件平台的地址信息栏中输入WEB版实验指导书的地址，在实验目录中选择“典型信号的概率密度分析实验”，建立实验环境。

图3 典型信号的概率密度分析实验环境下面是该实验的装配图和信号流图，图中的线上的数字为连接软件芯片的软件总线数据线号，**IC为使用的软件芯片。

图4 典型信号的概率密度分析实验装配图3.然后选择不同的信号类型，观察相关函数计算结果，并与相关函数的性质对照，进行实验结果分析。

六. 实验报告要求1.简述实验目的和原理。

1.拷贝实验系统运行界面，插入到Word格式的实验报告中，用Winzip压缩后通过Email上交实验报告。

广西铁道2021年第1期电务信号典型隐患案例剖析吕永红（柳州电务段，助理工程师，广西柳州545007）摘要：电务信号对铁路运输安全影响很大。

一些故障由于不容易发现，具有一定的隐蔽性，又会给铁路运输安全带来隐患，有的已干扰了正常的铁路运输秩序，影响了行车安全。

通过剖析柳州电务段全州南高铁电务车间几起典型隐患案例发生的原因，充分利用信号集中监测设备调阅分析，结合现场实际，提出增强责任感、落实责任制、树立大局意识、加强业务技能培训、严格作业程序等对策措施，防止类似故障的发生。

关键词：隐患原因剖析；对策措施1典型隐患案例1.1灯丝电流波动2017年12月11日调阅发现，东安东站X4信号机H灯灯丝电流，由145MA上升到152MA。

经查，隐患原因是灯室内组合内部信号机采集线头松动，引发灯丝电流波动。

1.2电缆绝缘变化趋势引发设备隐患2017年12月21日调阅发现，松川站2461G-FSH电缆绝缘由20兆欧，突然变化至1.8兆欧。

经查，隐患原因是全州站至松川站间2461GFS区段中XF～5（2503信号机处）电缆盒内有积水，致使5#、21#端子柱从根部断裂。

1.3轨道电路电压突升突降2018年2月7日调阅发现，中继4站2421AG的电压曲线在348mV～364mV之间波动变化。

变化规律是过车前后突升突降，没有列车通过时基本不会变化，且电压波动幅度不大，在30mV以内，小轨变化在154mV～160mV之间。

当主轨电压在349mV时，小轨是160mV；当主轨电压升高到367mV时，小轨降低到154m V。

经查，隐患原因是由于2421AG电容C6接触不良。

1.4电压波动2018年1月28日调阅发现，兴安北站7DG在4:35时，轨道的电路电压在16v～17.9v之间波动，变化规律是过车前后突升突降。

经查，隐患原因是兴安北站7#道岔地线碰转辙机外壳，引发轨道电路钢轨单边接地。

1.5曲线升高2018年2月12日调阅发现，全州南站6#道岔在12:08时，总功率曲线在300w～415w之间，变化规律是过车突升突降。

典型信号分析报告范文一、引言信号分析是一种在不同领域有着广泛应用的技术，通过对信号进行采集、处理和分析，可以帮助我们了解信号的特征、特点和规律。

本报告旨在通过对某典型信号的分析，展示信号分析所涉及的方法和技术，并阐述其在实际应用中的价值和意义。

二、信号概述我们选择了一段震动信号作为本次分析的对象。

震动信号是一种用于描述物体振动情况的信号，广泛应用于工程领域。

该信号包含了物体起伏和振动的信息，是分析物体结构和性能的重要指标。

三、信号采集与预处理为了获得震动信号，我们使用了一款专业的传感器进行采集，该传感器具有高精度和高灵敏度的特点。

在采集过程中，需要注意传感器的安装位置和环境条件，以保证采集到的信号准确有效。

在采集到信号后，我们对其进行了预处理。

预处理的目的是消除信号中的干扰和噪声，提高信号的有效性和可靠性。

我们采用了滤波、降噪和去除异常值等处理方法，确保信号的稳定性和可靠性。

四、信号特征提取信号特征提取是信号分析的重要步骤。

通过提取信号的特征，我们可以了解信号的频率、幅值、相位等关键参数，从而更好地理解信号的本质和特性。

在本次分析中，我们采用了频谱分析、时域分析和小波分析等方法，提取了信号的相关特征。

五、信号分析与解释在本次分析中，我们通过对震动信号进行频谱分析，发现信号中存在一定的频率成分和能量分布。

进一步分析后发现，震动信号存在周期性变化，且频谱图中出现峰值与信号起伏相对应。

这表明该信号可能与物体振动相关，并可以用于评估物体的稳定性和结构性能。

六、信号应用与展望震动信号在工程领域有着广泛的应用价值。

通过对震动信号进行分析，我们可以了解物体的振动情况，评估物体的稳定性和结构性能，从而指导工程项目的设计和改进。

同时，信号分析还可以应用于检测和故障诊断等领域，为工程实践带来更多的便利和效益。

未来，随着科学技术的不断发展，信号分析将会越来越重要。

我们可以进一步深入研究信号分析的方法和技术，提升信号处理和识别的能力，为更多领域的科研和工程实践提供支持和指导。

cca分析概述随着科技的不断发展，计算机科学领域不断涌现出新的研究和应用方向。

其中，CCA（Canonical Correlation Analysis，典型相关分析）作为一种多变量统计分析方法，在数据挖掘和模式识别等领域具有广泛的应用。

本文将对CCA进行详细的分析和讨论，介绍其原理、应用和相关的研究进展。

第一部分：CCA的原理CCA是一种统计方法，用于探索变量之间的相关性关系。

它通过寻找一种线性转换，将两组变量投影到低维子空间，使得在该子空间中两组变量的投影向量相关性最大。

换句话说，CCA可以通过最大化两组变量之间的相关性来发现它们之间的潜在联系。

具体来说，假设我们有两组变量X和Y，其中X包含n个样本和p个特征，Y包含n个样本和q个特征。

我们可以将X和Y分别表示为X=[x1,x2,...,xp]和Y=[y1,y2,...,yq]，其中xi和yj分别表示第i个样本的第j个特征。

CCA的目标是找到两个转换矩阵Wx和Wy，将X和Y映射到低维空间，使得映射后的变量能够最大化它们之间的相关性。

形式化地说，我们可以定义两个相关性系数ρi，用于衡量映射后的变量对应的两个特征的相关程度。

这两个相关系数可以表示为：ρi = corr(Tx[:,i], Ty[:,i]), i=1,2,...,min(p,q)其中Tx和Ty分别是X和Y在低维空间中的映射结果。

为了最大化相关系数ρi，CCA可以通过求解以下优化问题来实现：max correlation(X*Wx[:,i], Y*Wy[:,i])其中X*和Y*分别是X和Y的中心化版本，将样本均值减去。

通过求解上述优化问题，我们可以得到最优的映射矩阵Wx和Wy，将X和Y映射到相关性最大的低维空间。

第二部分：CCA的应用现实生活中，CCA广泛应用于多个领域，包括数据挖掘、模式识别、生物信息学等。

以下是一些CCA的典型应用场景：1. 语音信号处理：在语音识别任务中，CCA可以用于挖掘语音信号和语音识别结果之间的相关性，从而提高识别准确率。