当前位置：文档之家 › K-means聚类算法课件

K-means聚类算法课件

  • 格式：ppt
  • 大小：945.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

02-KMeans聚类PPT

02-KMeans聚类PPT

分群1 84
33.73%
分群2 114
45.78%
分群3 51
20.48%
K-Means聚类案例
%为便于可视化，仅选取6个属性维度中的两个维度进行绘图
figure; scatter(X(IDX==1,2),X(IDX==1,3),'rx') hold on scatter(X(IDX==2,2),X(IDX==2,3),'m+') scatter(X(IDX==3,2),X(IDX==3,3),'c*') plot(C(:,2),C(:,3),'ko','MarkerSize',4,'LineWidth',1.5) legend('Cluster 1','Cluster 2','Cluster 3','Centroids')
Matlab的K-Means函数
函数参数选项Param：
1. ‘Distance’(距离测度)：
‘sqEuclidean’ 欧式距离（默认时，采用此距离方式） ‘cityblock’ 绝度误差和，又称：L1 ‘cosine’ 针对向量 ‘correlation’ 针对有时序关系的值 ‘ hamming’ 只针对二进制数据
Matlab的K-Means函数
函数参数选项Param：
2. ‘Start’（初始质心位置选择方法）
‘sample’从A中随机选取K个质心点 ‘uniform’根据A的分布范围均匀的随机生成K个质心 ‘cluste’r 初始聚类阶段随机选择10%的A的子样本（此方
法初始使用‘sample’方法） ‘matrix’提供一K*N的矩阵，作为初始质心位置集合。

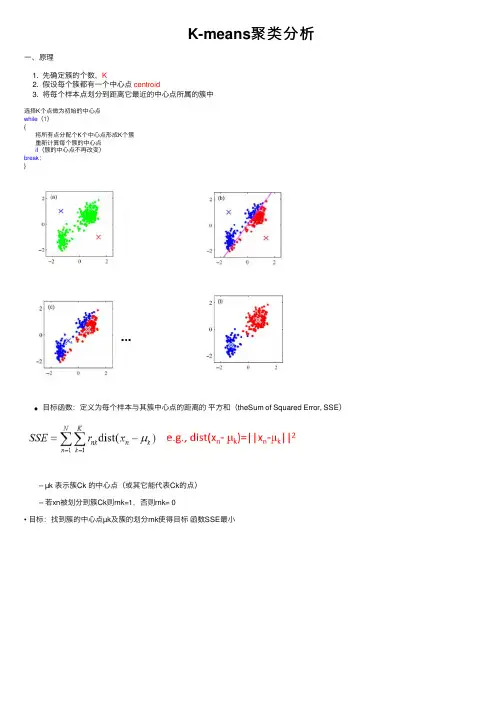
K-means聚类分析

K-means聚类分析

K-means聚类分析⼀、原理1. 先确定簇的个数，K2. 假设每个簇都有⼀个中⼼点centroid3. 将每个样本点划分到距离它最近的中⼼点所属的簇中选择K个点做为初始的中⼼点while（1）{将所有点分配个K个中⼼点形成K个簇重新计算每个簇的中⼼点if（簇的中⼼点不再改变）break；}⽬标函数：定义为每个样本与其簇中⼼点的距离的平⽅和（theSum of Squared Error, SSE） – µk 表⽰簇Ck 的中⼼点（或其它能代表Ck的点） – 若xn被划分到簇Ck则rnk=1，否则rnk= 0• ⽬标：找到簇的中⼼点µk及簇的划分rnk使得⽬标函数SSE最⼩初始中⼼点通常是随机选取的（收敛后得到的是局部最优解）不同的中⼼点会对聚类结果产⽣不同的影响：1、2、此时你⼀定会有疑问：如何选取"较好的"初始中⼼点？1. 凭经验选取代表点2. 将全部数据随机分成c类，计算每类重⼼座位初始点3. ⽤“密度”法选择代表点4. 将样本随机排序后使⽤前c个点作为代表点5. 从(c-1)聚类划分问题的解中产⽣c聚类划分问题的代表点 结论：若对数据不够了解，可以直接选择2和4⽅法需要预先确定K Q：如何选取K SSE⼀般随着K的增⼤⽽减⼩A：emmm你多尝试⼏次吧，看看哪个合适。

斜率改变最⼤的点⽐如k=2总结：简单的来说，K-means就是假设有K个簇，然后通过上⾯找初始点的⽅法，找到K个初始点，将所有的数据分为K个簇，然后⼀直迭代，在所有的簇⾥⾯找到找到簇的中⼼点µk及簇的划分rnk使得⽬标函数SSE最⼩或者中⼼点不变之后，迭代完成。

成功把数据分为K类。

预告：下⼀篇博⽂讲K-means代码实现。

KNN和Kmeans算法讲解PPT学习教案

KNN和Kmeans算法讲解PPT学习教案
第23页/共32页
算法概述-基本流程
1. 随机抽取k 个点作为初始 聚类的中心， 由各中心代表 各聚类
2.计算所有点 到这k个中心 的距离，并将 点归到离其最 近的聚类
3. 调整聚类 中心，即将 聚类的中心 移动到聚类 的几何中心 （即平均值）
4.重复第2、3步直到聚类的中 心不再移动，此时算法收敛
Action Action Unknown
点类型 Romance Romance Romance Action Action Action Unknown
第2页/共32页
K-NN算法是怎么来的
想一想：下面图片中只有三种豆，有三个豆是未知的种类，如何判定他们的 种类？
未知的豆离哪种豆最近就认为未知豆和该豆是同一种类。
点 3.对噪声和孤立数据敏
感
第28页/共32页
k-means-优缺点
初始化4个类别中心 左侧的全体数据仅与第一个类别中心相似
第29页/共32页
k-means-例子
一只遥望大海的小狗。此图为100×100像素的JPG图片，每个像素可以 表示为三维向量（分别对应红绿蓝三基色）。
要求使用k-means算法，将图片分割为合适的背景区域（三个）和前景 区域（小狗）。
第11页/共32页
全称：k-means 中文：K-均值聚类算法
第12页/共32页
聚类
聚类（Clustering）就是对大量未知标注的数据集，按数据的内 在相似性将数据集划分为多个族（Cluster），使族内的数据相似 度尽可能大而类别间的数据相似度尽可能小。
聚类中没有任何指导信息，完全按照数据的分布进行类别划 分
概况，这可以直接转化为针对不同客户的营销策略。
第15页/共32页

数据挖掘第12讲-聚类算法-kmeans

数据挖掘第12讲-聚类算法-kmeans

• 典型算法：K-MEANS算法（k均值）、K-MEDOIDS 算法（k中心）、CLARANS算法；
基于层次的算法 (hierarchical methods)
• 代表算法有：最短距离法、BIRCH算法、CURE算 法、CHAMELEON算法等；
基于密度的方法(densitybased methods)
������������(������, ������) =
1
������
������
෍ |������������ − ������������|������
������=1
（x > 0）
当x取1,2, ∞时，分别对应曼哈顿（Manhattan）距离、欧式 （Euclidean）距离、切比雪夫（Chebyshev）距离
• 类别划分策略（算法）
通过何种类别划分方式使类别划分结果达到有效性函数;
相似度
距离:
设使用n个指标特征变量来描述样本,那么我们就可以把每个样本点 看作n维空间的一个点,进而使用某种距离来表示样本点之间的相似 性,距离较近的样本点性质较相似,距离较远的样本点差异较大。
明可夫斯基（Minkowski）距离：������ = [������1, ������2, . . . , ������������ሿ ������ = [������1, ������2, . . . , ������������ሿ
优点：聚类时间快; 缺点：对初始参数敏感;容易陷入局部最优。
基于划分的聚类
思路：根据与类别中心的距离聚类，循环调整类别中心位置 有 N 个样本的集合Zs={Z1, Z2, ..., ZN}，想要聚成 K 个类（事先给定 K）
1 • 设置初始类别数K，人为设置K个类别中心;

K-means聚类算法ppt课件

K-means聚类算法ppt课件
K-means聚类算法
ppt课件.
1
K-means算法是很典型的基于距离的 聚类算法，采用距离作为相似性的评价指 标，即认为两个对象的距离越近，其相似 度就越大。
该算法认为类是由距离靠近的对象组 成的，因此把得到紧凑且独立的类作为最 终目标。
ppt课件.
2
假设数据集合为(x1, x2, …, xn)，并 且每个xi为d维的向量，K-means聚类的目 的是，在给定分类组数k（k ≤ n）值的条 件下，将原始数据分成k类：
ppt课件.
4
数学表达式：
n：样本数。 k：样本分为k类。 rnk：第n个样本点是否属于第k类，属于则
rnk=1， 不属于则rnk=0。 μK：第k个中心点。
ppt课件.
5
k-means 要做的就是最小化
这个函数。
迭代的方法： 1、固定μK，得到rnk。 2、固定rnk，求出最优的μK。
ppt课件.
ppt课件.
12
K- medoids算法流程如下： 1、任意选取K个对象作为初始中心点 （O1,O2,…Oi…Ok）。 2、将余下的对象分到各个类中去（根据与 中心点最相近的原则）； 3、对于每个类（Oi）中，顺序选取一个Or， 计算用Or代替Oi后的消耗—E（Or）。选择 E最小的那个Or来代替Oi。这样K个中心点 就改变了。
。不过，加上归一化规定，一个数据点的 隶属度的和总等于1：
ppt课件.
21
把n个元素xi（i=1,2,…,n）分为c个模糊组， 目标函数：
其中，m是大于1的实数，加权实数。uij 是xi属于类别j隶属度，cj是 类j的聚类中心。
ppt课件.
22
算法步骤： 1、用值在0，1间的随机数初始化隶属矩阵U，

第二讲聚类Kmeans算法跟运用（K-meanscluster）

第二讲聚类Kmeans算法跟运用（K-meanscluster）

第⼆讲聚类Kmeans算法跟运⽤（K-meanscluster）CLEMENTINE 1212 CLEMENTINE--SEGMENTATION（K-MEANS）何谓集群分析何谓集群分析((CLUSTERING ANALYSIS )集群分析是⼀种将样本观察值进⾏分析，具有某些共同特性者予以整合在⼀起，再将之分配到特定的群体，最后形成许多不同集群的⼀种分析⽅法。

Clementine 12.0中提供的集群分析⽅法有三种：1. K-means2. Two-step3. KohonenK-MEANS的理论背景K-Means是集群分析(Cluster Analysis)中⼀种⾮阶层式((Nonhierarchical))的演算⽅法，由J. B. Mac Queen于1967年正式发表，也是最早的组群化计算技术。

其中，⾮阶层式则是指在各阶段分群过程中，将原有的集群予以打散，并重新形成新的集群。

K-Means是⼀种前设式群集算法，也就是说必须事前设定群集的数量，然后根据此设定找出最佳群集结构。

⽽K-Means算法最主要的概念就是以集群内资料平均值为集群的中⼼。

计算距離并分群的中⼼点重新计算新的距離并分群不断重复步骤三四，直到所设计的停⽌条件发⽣。

⼀般是以没有任何对象变换所属集群为停⽌绦件，也就是所谓的s q u a r e -e r r o r c r i t e r i o n ：代表集群的中⼼(平均数)，是集群内的物件，则代表集群。

210iKi p CiE p m =∈=?=∑∑i m i p i iC iK-MEANS的基本需求与优缺点建⽴K-means模型的要求：需要⼀个以上的In字段。

⽅向为Out、Both、None的字段将被忽略。

优点：建⽴K-means模型不需要分组数据。

对于⼤型数据集，K-means模型常常是最快的分群⽅法。

缺点：对于初始值的选择相当敏感，选择不同的初始值，可能会导致不同的分群结果。

聚类 课件

根据某种模型进行聚类，如高斯混合 模型、神经网络聚类等。
基于网格的聚类算法
将数据空间划分为网格，然后在网格 上进行聚类，如STING算法、 CLIQUE算法等。
02
K-means聚类算法
K-means算法的原理
K-means算法是一种基于距离的聚 类算法，通过迭代过程将数据点划分 为K个聚类，使得每个数据点与其所 在聚类的中心点之间的距离之和最小 。
DBSCAN算法的步骤
01 扫描所有点，标记为核心点、边界点和噪 声点。
02 对于每个核心点，以其为起点，扩展与其 密度相连的区域。
03
将扩展的区域内的所有点标记为同一簇。
04
重复上述步骤，直到所有点都被处理。
DBSCAN算法的优缺点
01
优点
02
对异常值具有较强的鲁棒性。
能够发现任何形状的簇。
03
互信息
总结词
衡量聚类结果与真实类别之间相似度的指标，值越大表示聚 类效果越好。
详细描述
互信息是一种衡量聚类结果与真实类别之间相似度的指标， 其计算方法为聚类结果与真实类别之间的熵值之差。如果聚 类效果好，则聚类结果与真实类别之间的相似度会较高，熵 值之差会较小，因此互信息值会较大。
调整兰德指数
总结词
步骤2
重复以下步骤，直到满足终止条件
• 步骤2.1
将每个数据点与最近的簇中心点合并，形成新的 簇中心点。
• 步骤2.2
更新簇中心点为新合并的簇中所有点的平均值或中 心点。
• 步骤2.3
重复步骤2.1和步骤2.2，直到所有数据点都归入某 个簇或达到预设的簇数量。
输出聚类结果。
步骤3
层次聚类算法的优缺点
DBSCAN算法的优缺点

K-means算法讲解ppt课件

完整最新ppt 19
预测：预测是通过分类或估值起作用的，也就是说，通过 分类或估值得出模型，该模型用于对未知变量的预言。
聚类：在没有给定划分类的情况下，根据信息相似度将信 息分组。是一种无指导的学习。
关联规则：揭示数据之间的相互关系，而这种关系没有在 数据中直接表现出来。
偏差检测： 用于发现与正常情况不同的异常和变化。并分 析这种变化是有意的欺诈行为还是正常的变化。如果是异常 行为就采取预防措施。
完整最新ppt
13
决定性因素
Input & centroids
①数据的采集和抽象 ②初始的中心选择
Selected k
① k值的选定
MaxIterations & Convergence
①最大迭代次数 ②收敛值
factors？
Meassures
①度量距离的手段
完整最新ppt
14
主要因素
初始中 心点
Repeat 从簇表中取出一个簇
（对选定的簇进行多次二分实验） for i=1 to实验次数 do 试用基本K均值（k=2），二分选定的簇 end for 从实验中选取总SSE最小的两个簇添加到簇表中
Until 簇表中包含K个簇
17
谢谢！
完整最新ppt
18
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
6
什么是Kmeans算法？
Q1：K是什么？A1：k是聚类算法当中类的个数。 Q2：means是什么？A2：means是均值算法。
Summary：Kmeans是用均值算法把数 据分成K个类的算法！
完整最新ppt
7
Kmeans算法详解（1）

Kmeans聚类算法ppt课件


（5）对于“噪声”和孤立点数据敏感。
精选版课件ppt
8
K-means缺点以及改进 （1）要求用户必须事先给出要生成的簇的数目k。这个k并不是最好的。 解决：肘部算法 肘部算法是一种启发式方法来估计最优聚类数量，称为肘部法则（Elbow Method）。
各个类畸变程度（distortions）之和；每个类的畸变程度等于该类重心与其内 部成员位置距离的平方和；最优解以成本函数最小化为目标，其中uk是第k个 类的重心位置
第一次
第二次
精选版课件ppt
17
八、K-means聚类算法
在第五次迭代时，得到的三个簇与第四迭代结果相同，而且准则函数E收敛，迭代 结束，结果如下表所示：
k为迭代次数
精选版课件ppt
18
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
精选版课件ppt
精选版课件ppt
3
八、K-means聚类算法
2. K-means聚类算法原理 K-Means算法的工作框架：
（1）给出 n 个数据样本,令 I 1,随机选择 K 个初始聚类中心 Z j (I) , j 1, 2,3,, K ；
（2）求解每个数据样本与初始聚类中心的距离 D xi , Z j I ,i 1, 2,3,, n
假设A、B、C、D的D(x)如上图所示，当算法取值Sum(D(x))*random 时，该值会以较大的概率落入D(x)较大的区间内，所以对应的点会以 较大的概率被选中作为新的聚类中心。
精选版课件ppt
10
八、K-means聚类算法
3 K-means聚类算法特点及应用 3.2 K-means聚类算法应用
i=1,2
精选版课件ppt

机器学习kmeans聚类算法与应用

机器学习算法day02_Kmeans聚类算法及应用课程大纲Kmeans聚类算法原理Kmeans聚类算法概述Kmeans聚类算法图示Kmeans聚类算法要点Kmeans聚类算法案例需求用Numpy手动实现用Scikili机器学习算法库实现Kmeans聚类算法补充算法缺点改良思路课程目标：1、理解Kmeans聚类算法的核心思想2、理解Kmeans聚类算法的代码实现3、掌握Kmeans聚类算法的应用步骤：数据处理、建模、运算和结果判定1.Kmeans聚类算法原理1.1概述K-means算法是集简单和经典于一身的基于距离的聚类算法采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

该算法认为类簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

1.2算法图示假设我们的n个样本点分布在图中所示的二维空间。

从数据点的大致形状可以看出它们大致聚为三个cluster，其中两个紧凑一些，剩下那个松散一些，如图所示：我们的目的是为这些数据分组，以便能区分出属于不同的簇的数据，给它们标上不同的颜色，如图：1.3算法要点1.3.1核心思想通过迭代寻找k个类簇的一种划分方案，使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。

k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。

k-means算法的基础是最小误差平方和准则,其代价函数是：式中，μc(i)表示第i个聚类的均值。

各类簇内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数无法用解析的方法最小化，只能有迭代的方法。

1.3.2算法步骤图解下图展示了对n个样本点进行K-means聚类的效果，这里k取2。

1.3.3算法实现步骤k-means算法是将样本聚类成k个簇（cluster），其中k是用户给定的，其求解过程非常直观简单，具体算法描述如下：1)随机选取k个聚类质心点2)重复下面过程直到收敛{对于每一个样例i，计算其应该属于的类：对于每一个类j，重新计算该类的质心：}其伪代码如下：********************************************************************创建k个点作为初始的质心点（随机选择）当任意一个点的簇分配结果发生改变时对数据集中的每一个数据点对每一个质心计算质心与数据点的距离将数据点分配到距离最近的簇对每一个簇，计算簇中所有点的均值，并将均值作为质心2.Kmeans分类算法Python实战2.1需求对给定的数据集进行聚类本案例采用二维数据集，共80个样本，有4个类。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。