双曲线的标准方程
- 格式:doc
- 大小:16.00 KB
- 文档页数:2

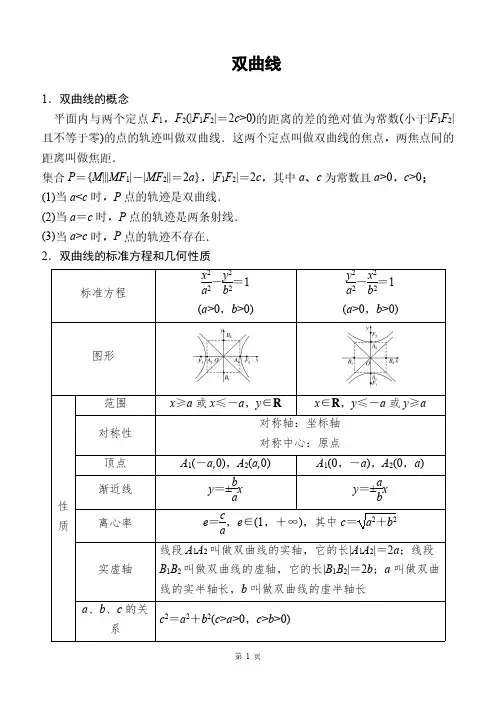
双曲线1.双曲线的概念平面内与两个定点F 1,F 2(|F 1F 2|=2c >0)的距离的差的绝对值为常数(小于|F 1F 2|且不等于零)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做焦距.集合P ={M |||MF 1|-|MF 2||=2a },|F 1F 2|=2c ,其中a 、c 为常数且a >0,c >0;(1)当a <c 时,P 点的轨迹是双曲线.(2)当a =c 时,P 点的轨迹是两条射线.(3)当a >c 时,P 点的轨迹不存在.2.双曲线的标准方程和几何性质标准方程x 2a 2-y 2b 2=1(a >0,b >0)y 2a 2-x 2b 2=1(a >0,b >0)图形性质范围x ≥a 或x ≤-a ,y ∈R x ∈R ,y ≤-a 或y ≥a对称性对称轴:坐标轴对称中心:原点顶点A 1(-a,0),A 2(a,0)A 1(0,-a ),A 2(0,a )渐近线y =±b axy =±a bx离心率e =ca,e ∈(1,+∞),其中c =a 2+b 2实虚轴线段A 1A 2叫做双曲线的实轴,它的长|A 1A 2|=2a ;线段B 1B 2叫做双曲线的虚轴,它的长|B 1B 2|=2b ;a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长a 、b 、c 的关系c 2=a 2+b 2(c >a >0,c >b >0)1.方程x 2m -y 2n=1(mn >0)表示的曲线(1)当m >0,n >0时,表示焦点在x 轴上的双曲线.(2)当m <0,n <0时,则表示焦点在y 轴上的双曲线.2.方程的常见设法(1)与双曲线x 2a 2-y 2b 2=1共渐近线的方程可设为x 2a 2-y 2b 2=λ(λ≠0).(2)若渐近线的方程为y =±b a x ,则可设双曲线方程为x 2a 2-y 2b 2=λ(λ≠0).3.常用结论1.双曲线的焦点到其渐近线的距离为b .2.若P 是双曲线右支上一点,F 1,F 2分别为双曲线的左、右焦点,则|PF 1|min =a +c ,|PF 2|min =c -a .3.同支的焦点弦中最短的为通径(过焦点且垂直于长轴的弦),其长为2b 2a ;异支的弦中最短的为实轴,其长为2a .4.若P 是双曲线上不同于实轴两端点的任意一点,F 1,F 2分别为双曲线的左、右焦点,则S △PF 1F 2=b 2tan θ2,其中θ为∠F 1PF 2.5.若P 是双曲线x 2a 2-y 2b 2=1(a >0,b >0)右支上不同于实轴端点的任意一点,F 1,F 2分别为双曲线的左、右焦点,I 为△PF 1F 2内切圆的圆心,则圆心I 的横坐标为定值a .6.等轴双曲线(1)定义:中心在原点,以坐标轴为对称轴,实半轴长与虚半轴长相等的双曲线叫做等轴双曲线.(2)性质:①a =b ;②e =2;③渐近线互相垂直;④等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项.7.共轭双曲线(1)定义:如果一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴,那么这两条双曲线互为共轭双曲线.(2)性质:①它们有共同的渐近线;②它们的四个焦点共圆;③它们的离心率的倒数的平方和等于1.1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)平面内到点F 1(0,4),F 2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.()(2)平面内到点F 1(0,4),F 2(0,-4)距离之差等于6的点的轨迹是双曲线.()(3)方程x 2m -y 2n=1(mn >0)表示焦点在x 轴上的双曲线.((4).双曲线x 2m 2-y 2n 2=λ(m >0,n >0,λ≠0)的渐近线方程是m (5).若双曲线x )x ±ny =0.( )2a 2-y 2b 2=1(a >0,b >0)与x 2b 2-y 2a 2=1(a >0,b >0)的离心率分别是e 1,e 2,则1e 21+1e 222.双曲线2x 2-y 2=8的实轴长是=1(此条件中两条双曲线称为共轭双曲线).( )()A .2B .22C .4D .423.(2021·全国甲卷)点(3,0)到双曲线x 216-y 29=1的一条渐近线的距离为()A.95B.85C.65D.454.(教材改编)过双曲线x 2-y 2=8的左焦点F 1有一条弦PQ 在左支上,若|PQ |=7,F 2是双曲线的右焦点,则△PF 2Q 的周长是()A .28B .14-82C .14+82D .825.已知双曲线E :x 216-y 2m 2=1的离心率为54,则双曲线E 的焦距为__________.双曲线的定义的应用例题:(1)已知定点F 1(-2,0),F 2(2,0),N 是圆O :x 2+y 2=1上任意一点,点F 1关于点N 的对称点为M ,线段F 1M 的中垂线与直线F 2M 相交于点P ,则点P 的轨迹是()A .椭圆B .双曲线C .抛物线D .圆(2)已知动圆M 与圆C 1:(x +4)2+y 2=2外切,与圆C 2:(x -4)2+y 2=2内切,则动圆圆心M 的轨迹方程为()A.x 22-y 216=1(x ≤-2) B.x 22-y 214=1(x ≥2)C.x 22-y 216=1 D.x 22-y 214=1(3)已知圆C 1:(x +3)2+y 2=1和圆C 2:(x -3)2+y 2=9,动圆M 同时与圆C 1及圆C 2相外切,则动圆圆心M 的轨迹方程为______________(4)已知F 1,F 2为双曲线C :x 2-y 2=1的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则|PF 1|·|PF 2|=__________.(5)已知F 1,F 2是双曲线x 24-y 2=1的两个焦点,P 在双曲线上,且满足∠F 1PF 2=90°,则△F 1PF 2的面积为()A .1B .52C .2D .5(6).(2020·全国卷Ⅲ)设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,离心率为5.P 是C 上一点,且F 1P ⊥F 2P .若△PF 1F 2的面积为4,则a =()A .1B .2C .4D .8(7)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,左、右焦点分别为F 1,F 2,点A 在双曲线C 上,若△AF 1F 2的周长为10a ,则△AF 1F 2的面积为()A .215a 2B .15a 2C .30a 2D .15a 2(8)P 是双曲线C :x 22-y 2=1右支上一点,直线l 是双曲线C 的一条渐近线.P 在l上的射影为Q ,F 1是双曲线C 的左焦点,则|PF 1|+|PQ |的最小值为()A .1B .2+155C .4+155D .22+1(9)已知双曲线x2-y2=4,F1是左焦点,P1,P2是右支上的两个动点,则|F1P1|+|F1P2|-|P1P2|的最小值是()A.4B.6C.8D.16(10)双曲线C的渐近线方程为y=±233x,一个焦点为F(0,-7),点A的坐标为(2,0),点P为双曲线第一象限内的点,则当点P的位置变化时,△P AF周长的最小值为()A.8B.10C.4+37D.3+317双曲线的标准方程求双曲线标准方程的方法:(1)定义法(2)待定系数法①当双曲线焦点位置不确定时,设为Ax2+By2=1(AB<0);②与双曲线x2a2-y2b2=1共渐近线的双曲线方程可设为x2a2-y2b2=λ(λ≠0);③与双曲线x2a2-y2b2=1共焦点的双曲线方程可设为x2a2-k-y2b2+k=1(-b2<k<a2).例题:(1)根据下列条件,求双曲线的标准方程:(1)虚轴长为12,离心率为54;(2)焦距为26,且经过点M(0,12);(3)经过两点P(-3,27)和Q(-62,-7).(2)双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左焦点为(-3,0),且C 的离心率为32,则双曲线C 的方程为()A.y 24-x 25=1 B.y 25-x 24=1 C.x 24-y 25=1 D.x 25-y 24=1(3)已知双曲线过点(2,3),渐近线方程为y =±3x ,则该双曲线的标准方程是()A.7x 216-y 212=1 B.y 23-x 22=1C .x 2-y 23=1D.3y 223-x 223=1(4)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为y =52x ,且与椭圆x 212+y 23=1有公共焦点,则C 的方程为()A .x 28-y 210=1B .x 24-y 25=1C .x 25-y 24=1D .x 24-y 23=1(5)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)过点(2,3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,则双曲线C 的标准方程是()A .x12-y 2=1B .x 29-y 23=1C .x 2-y 23=1D .x 223-y 232=1(6)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为()A .x 24-y 212=1B .x 212-y 24=1C .x 23-y 29=1D .x 29-y 23=1(7)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,点M 在双曲线的右支上,点N 为F 2M 的中点,O 为坐标原点,|ON |-|NF 2|=2b ,∠ONF 2=60°,△F 1MF 2的面积为23,则该双曲线的方程为__________.双曲线的几何性质求双曲线的渐近线方程例:(1)已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2,则双曲线C 的渐近线方程为()A .y =±3xB .y =±33x C .y =±12xD .y =±2x(2)已知双曲线T 的焦点在x 轴上,对称中心为原点,△ABC 为等边三角形.若点A 在x 轴上,点B ,C 在双曲线T 上,且双曲线T 的虚轴为△ABC 的中位线,则双曲线T 的渐近线方程为()A .y =±153xB .y =±53xC .y =±33x D .y =±55x (3)已知椭圆x 2a 2+y 2b 2=1(a >b >0)与双曲线x 2a 2-y 2b 2=12的焦点相同,则双曲线的渐近线方程为()A .y =±3xB .y =±33x C .y =±22x D .y =±2x(4)已知F 1,F 2分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,以F 1F 2为直径的圆与双曲线在第一象限和第三象限的交点分别为M ,N ,设四边形F 1NF 2M 的周长为p ,面积为S ,且满足32S =p 2,则该双曲线的渐近线方程为()A .y =±32x B .y =±233xC .y =±12xD .y =±22x求双曲线的离心率(范围)例:(1)(2021·全国甲卷)已知F 1,F 2是双曲线C 的两个焦点,P 为C 上一点,且∠F 1PF 2=60°,|PF 1|=3|PF 2|,则C 的离心率为()A.72B.132C.7D.13(2).已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若F 1A →=AB →,F 1B →·F 2B →=0,则C 的离心率为__________.(3)设F 为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的右焦点,过坐标原点O 的直线与双曲线C 的左、右支分别交于点P ,Q ,若|PQ |=2|QF |,∠PQF =60°,则该双曲线的离心率为()A .3B .1+3C .2+3D .4+23(4)(2020·全国卷Ⅲ)设双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,离心率为5.P 是C 上一点,且F 1P ⊥F 2P .若△PF 1F 2的面积为4,则a =()A .1B .2C .4D .8(5)圆C :x 2+y 2-10y +16=0上有且仅有两点到双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线的距离为1,则该双曲线离心率的取值范围是()A .(2,5)B.⎪⎭⎫⎝⎛2535,C.⎪⎭⎫⎝⎛2545,D .(5,2+1)双曲线几何性质的综合应用例:(1)已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1,F 2是C 的两个焦点,若MF 1→·MF 2→<0,则y 0的取值范围是()A.⎪⎪⎭⎫⎝⎛-3333, B.⎪⎪⎭⎫⎝⎛-6363,C.⎪⎪⎭⎫⎝⎛-322322, D.⎪⎪⎭⎫⎝⎛-332332,逻辑推理(2020·新高考卷Ⅰ)(多选)已知曲线C :mx 2+ny 2=1.()A .若m >n >0,则C 是椭圆,其焦点在y 轴上B .若m =n >0,则C 是圆,其半径为nC .若mn <0,则C 是双曲线,其渐近线方程为y =±-m nx D .若m =0,n >0,则C 是两条直线直线与双曲线的位置关系例题:若双曲线E :x 2a 2-y 2=1(a >0)的离心率等于2,直线y =kx -1与双曲线E 的右支交于A ,B 两点.(1)求k 的取值范围;(2)若|AB |=63,求k 的值.双曲线课后练习1.方程x2m+2+y2m-3=1表示双曲线的一个充分不必要条件是()A.-3<m<0B.-1<m<3C.-3<m<4D.-2<m<3 2.在平面直角坐标系中,已知双曲线C与双曲线x2-y23=1有公共的渐近线,且经过点P(-2,3),则双曲线C的焦距为()A.3B.23C.33D.433.设双曲线C:x2-4y2+64=0的焦点为F1,F2,点P为C上一点,|PF1|=6,则|PF2|为()A.13B.14C.15D.224.若双曲线C:x2a2-y2b2=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则C的渐近线方程为()A.y=±13x B.y=±33x C.y=±3x D.y=±3x5.若双曲线C:x2a2-y2b2=1(a>0,b>0)的右顶点A到一条渐近线的距离为223a,则双曲线的离心率为()A.223B.13C.3D.226.已知双曲线的一个焦点F(0,5),它的渐近线方程为y=±2x,则该双曲线的标准方程为_____________7.已知双曲线x24-y25=1的左焦点为F,点P为其右支上任意一点,点M的坐标为(1,3),则△PMF周长的最小值为()A.5+10B.10+10C.5+13D.9+138.已知直线l与双曲线C:x2-y2=2的两条渐近线分别交于A,B两点,若AB 的中点在该双曲线上,O为坐标原点,则△AOB的面积为()A.12B.1C.2D.49.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,P 为双曲线上一点,且|PF 1|=2|PF 2|.若cos ∠F 1PF 2=14,则该双曲线的离心率等于()A.22 B.52C .2 D.3+110.(2020·全国卷Ⅱ)设O 为坐标原点,直线x =a 与双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的两条渐近线分别交于D ,E 两点.若△ODE 的面积为8,则C 的焦距的最小值为()A .4B .8C .16D .3211.双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线交双曲线左支于A ,B 两点,△F 2AB 是以A 为直角顶点的直角三角形,且∠AF 2B =30°,若该双曲线的离心率为e ,则e 2=()A .11+43B .13+53C .16-63D .19-10312.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的右焦点为F ,以F 为圆心和双曲线的渐近线相切的圆与双曲线的一个交点为M ,且MF 与双曲线的实轴垂直,则双曲线C 的离心率为()A.52 B.5C.2D .213.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的实轴长为8,右焦点为F ,M 是双曲线C 的一条渐近线上的点,且OM ⊥MF ,O 为坐标原点,若S △OMF =6,则双曲线C 的离心率为)______________14.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,离心率为3,点P 为双曲线上一点,∠F 1PF 2=120°,则双曲线的渐近线方程为__________;若双曲线C 的实轴长为4,则△F 1PF 2的面积为__________.15.已知F 1,F 2分别是双曲线x 2-y 2b 2=1(b >0)的左、右焦点,A 是双曲线上在第一象限内的点,若|AF 2|=2且∠F 1AF 2=45°,延长AF 2交双曲线的右支于点B ,则△F 1AB 的面积等于_____________16.设双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线分别交双曲线的左、右两支于M ,N .若以MN 为直径的圆经过右焦点F 2,且|MF 2|=|NF 2|,则双曲线的离心率为____________.17.已知点P (1,3)在双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的渐近线上,F 为双曲线C 的右焦点,O 为原点.若∠FPO =90°,则双曲线C 的方程为_____________,其离心率为__________.18.已知双曲线x 2-y 23=1的左顶点为A 1,右焦点为F 2,P 为双曲线右支上一点,则P A 1→·PF 2→的最小值为________.19.(2021·山东淄博二模)已知动点P 在双曲线C :x 2-y 23=1上,双曲线C 的左、右焦点分别为F 1,F 2,下列结论错误的是()A .C 的离心率为2B .C 的渐近线方程为y =±3xC .动点P 到两条渐近线的距离之积为定值D .当动点P 在双曲线C 的左支上时,|PF 1||PF 2|2的最大值为14。




双曲线及其标准方程
双曲线及其标准方程
双曲线(Hyperbola)是指与平面上到两个定点的距离之差的绝对值为定值的点的轨迹,也可以定义为到定点与定直线的距离之比是一个大于1的常数的点之轨迹[1]。
双曲线是圆锥曲线的一种,即圆锥面与平行于中轴的平面的交截线。
设双曲线的焦距为2c,双曲线上任意一点到焦点F1,F2的距离的差的绝对值等于常数2a(c>a>0)[2]
以F1,F2所在直线为x轴,线段F1F2的垂直平分线为y轴,建立直角坐标系xOy,则F1,F2的坐标分别为(-c,0),(c,0)设M(x,y)为双曲线上任意一点,根据双曲线定义知
|MF1-MF2|=2a
即
以上两种方程都叫做双曲线的标准方程p。
方程推导:
椭圆和双曲线标准方程的推导方法大致有两种:一种是教材上移项平方的方法,另一种是资料上常见的构造对偶式的方法.这两种方法的运算量都比较大,尤其前一种方法需要两次移项平方.最近,笔者在进行椭圆的教学时,又发现了一种运算量较小的办法,即根据圆和椭圆的方程都具备“二元二次”的特征,可通过构造圆的方程能简化椭圆标准方程的推导过程,而该方法也同样适用于双曲线标准方程
的推导。



双曲线的标准方程推导双曲线是数学中的一种重要的曲线类型,它在几何、代数以及物理等领域都有着广泛的应用。
在本文中,我们将介绍双曲线的标准方程推导过程,通过推导我们可以更好地理解双曲线的性质和特点。
首先,我们来定义双曲函数。
双曲函数是指满足关系式x^2 y^2 = 1的函数。
双曲函数分为两种类型,分别为双曲余弦函数和双曲正弦函数,它们的定义如下:双曲余弦函数定义为,cosh(x) = (e^x + e^(-x))/2。
双曲正弦函数定义为,sinh(x) = (e^x e^(-x))/2。
接下来,我们将推导双曲线的标准方程。
首先,我们考虑双曲余弦函数的图像。
根据双曲余弦函数的定义,我们可以得到:cosh^2(x) sinh^2(x) = 1。
现在,我们将cosh^2(x)和sinh^2(x)分别表示为u和v,即:u = cosh^2(x)。
v = sinh^2(x)。
那么,我们可以得到:u v = 1。
这就是双曲线的标准方程。
在平面直角坐标系中,双曲线的标准方程可以表示为x^2/a^2 y^2/b^2 = 1或者y^2/b^2 x^2/a^2 = 1,其中a和b分别为双曲线在x轴和y轴上的焦点距离。
通过这个推导过程,我们可以看出双曲线的标准方程与双曲函数之间的联系。
双曲函数是双曲线的基本构成要素,而双曲线的标准方程则是描述双曲线几何性质的重要方程。
另外,双曲线还具有许多重要的性质,比如双曲线的渐近线、焦点、直径等。
这些性质在物理学、工程学以及经济学中都有着重要的应用,特别是在光学、电磁学、天文学等领域。
总之,双曲线的标准方程推导是我们理解双曲函数和双曲线性质的重要基础。
通过本文的介绍,相信读者对双曲线有了更深入的了解,希望本文能对大家有所帮助。

双曲线的标准方程b双曲线是解析几何中一种重要的曲线,它具有许多独特的性质和特点。
在数学和物理学中,双曲线的应用非常广泛,因此了解双曲线的标准方程b对于深入理解其性质和应用至关重要。
首先,我们来看一下双曲线的定义。
双曲线是平面上一种特殊的曲线,其定义是平面上满足特定几何性质的点的集合。
双曲线有两条渐近线,它们分别与双曲线的两个分支无限靠近,但永远不会相交。
双曲线的标准方程b可以通过以下步骤推导得到。
双曲线的标准方程b可以表示为,$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$,其中a和b分别代表双曲线在x轴和y轴上的焦点到中心的距离。
在这个标准方程中,a 和b的取值对于双曲线的形状和性质有着重要的影响。
接下来,我们来详细解释一下双曲线标准方程中的参数a和b的含义。
首先,当a>b时,双曲线的两个分支分别朝左右无限延伸;当a<b时,双曲线的两个分支分别朝上下无限延伸。
而当a=b时,双曲线化为两条互相垂直的渐近线。
因此,参数a和b的取值直接影响了双曲线的形状和方向。
另外,双曲线的标准方程b还可以通过参数方程来表示。
参数方程为,$x=a\cosh t, y=b\sinh t$,其中参数t为实数。
通过参数方程,我们可以更直观地理解双曲线的形状和特点,进一步深入研究其性质和应用。
除了了解双曲线的标准方程b之外,我们还可以通过一些实例来加深对双曲线的理解。
例如,双曲线在物理学中的应用非常广泛,特别是在光学和电磁学领域。
双曲线的反射性质和聚焦性质使其成为许多光学器件和电磁场的重要研究对象。
通过实际例子的分析,我们可以更好地理解双曲线的特点和应用,为进一步研究和应用双曲线打下坚实的基础。
总之,双曲线的标准方程b是深入了解双曲线性质和应用的重要基础。
通过对双曲线标准方程b的推导和参数方程的解释,我们可以更好地理解双曲线的形状和特点。
同时,通过实例的分析,我们可以加深对双曲线的应用和意义的理解。
双曲线标准方程双曲线是解析几何中常见的一种曲线,它具有许多特殊的性质和规律。
在数学中,我们经常会遇到双曲线,并需要对其进行研究和分析。
为了更好地理解双曲线,我们需要了解其标准方程及相关知识。
首先,让我们来了解一下双曲线的定义。
双曲线是平面上的一种曲线,其定义方式可以有多种,其中一种常见的定义是,平面上的一点到两个给定点的距离之差等于常数的点的轨迹。
这个定义可以帮助我们直观地理解双曲线的形状和特点。
接下来,我们来看一下双曲线的标准方程。
双曲线的标准方程通常可以表示为:$\frac{x^2}{a^2} \frac{y^2}{b^2} = 1$。
或者。
$\frac{y^2}{b^2} \frac{x^2}{a^2} = 1$。
其中,a和b分别为双曲线在x轴和y轴上的焦点到原点的距离。
这两种形式的标准方程分别对应着双曲线的横轴和纵轴方向的开口方向。
在这里,我们可以看到双曲线的标准方程与椭圆和抛物线的标准方程有一定的相似之处,但又有着明显的区别。
通过对比这些曲线的标准方程,我们可以更好地理解它们的形状和特点。
双曲线的标准方程中的参数a和b对于确定双曲线的形状起着关键作用。
当a和b分别为正数时,双曲线的形状会有所不同,我们可以通过调整这些参数来观察双曲线的变化规律,从而更深入地理解双曲线的性质。
除了标准的双曲线方程外,我们还可以遇到其他形式的双曲线方程,例如双曲线的一般方程。
在实际问题中,我们可能会遇到各种各样的双曲线方程,因此掌握双曲线的标准方程及其相关知识对于我们解决问题至关重要。
双曲线作为解析几何中的重要内容,其在数学、物理、工程等领域都有着广泛的应用。
通过对双曲线标准方程的学习和掌握,我们可以更好地理解双曲线的性质和规律,为我们的学习和工作提供更多的帮助。
总之,双曲线标准方程是我们学习和研究双曲线的重要基础,通过对双曲线标准方程的深入理解,我们可以更好地应用双曲线的相关知识,解决实际问题,推动数学和其他领域的发展。
双曲线及其标准方程双曲线是代数曲线中的一种,它具有许多重要的性质和特点,在数学和物理学中有着广泛的应用。
双曲线的标准方程是描述双曲线的一种数学表达式,通过标准方程我们可以更清晰地了解双曲线的形状和特点。
本文将对双曲线及其标准方程进行详细的介绍和解析,希望能够帮助读者更深入地理解这一数学概念。
首先,让我们来了解一下什么是双曲线。
双曲线是平面上的一种曲线,它的形状类似于两条平行的直线。
双曲线分为两种类型,分别是椭圆双曲线和双曲双曲线。
椭圆双曲线的标准方程为x^2/a^2 y^2/b^2 = 1,而双曲双曲线的标准方程为x^2/a^2y^2/b^2 = -1。
其中,a和b分别代表双曲线在x轴和y轴上的截距,通过这两个参数我们可以确定双曲线的大小和形状。
接下来,我们来看一下双曲线的标准方程。
对于椭圆双曲线来说,当a^2 > b^2时,双曲线开口朝x轴,而当a^2 < b^2时,双曲线开口朝y轴。
而对于双曲双曲线来说,无论a和b的取值如何,双曲线始终开口朝x轴和y轴。
通过这些性质,我们可以更加直观地理解双曲线的形状和特点。
双曲线在数学和物理学中有着广泛的应用。
在数学中,双曲线常常出现在代数曲线的研究中,它们具有独特的性质和方程形式,对于研究者来说具有很高的研究价值。
在物理学中,双曲线则常常出现在光学和电磁学的研究中,它们可以描述电磁波的传播和折射规律,对于解决实际问题具有重要的意义。
总结一下,双曲线是一种重要的代数曲线,它具有独特的形状和特点。
通过标准方程,我们可以更清晰地了解双曲线的形状和特点。
双曲线在数学和物理学中有着广泛的应用,对于研究者和工程师来说具有重要的意义。
希望本文能够帮助读者更深入地理解双曲线及其标准方程,为他们的学习和研究提供帮助。
双曲线在y轴上的标准方程双曲线是几何学中一类具有重要理论意义的曲线,它包括简单的双曲线和平面双曲线。
本文将讨论它在y轴上的标准方程。
双曲线的定义是,它是一种曲线,它的每一条曲线都有一定的标准方程,以及两个焦点和两个极点。
它有两个参数,即离心率ε和焦距2a,ε和a决定了双曲线的形状。
它在y轴上的标准方程是:$$frac { { x }^{ 2 } }{ { a }^{ 2 } } - frac{ { y }^{ 2 } }{ { b }^{ 2 } } = 1 $$其中,离心率$$varepsilon$$和焦距2a都可以表达为:$$varepsilon = frac { b }{ a } a = frac { b }{ sqrt { varepsilon ^ { 2 } - 1 } } $$从上述的标准方程可以看出,双曲线的性质主要由离心率ε和焦距2a决定,离心率ε控制着曲线四边的弧度以及曲线的弯曲幅度,焦距2a控制着曲线的尺寸大小。
此,ε和a的大小决定了双曲线的形状,它们可以通过它们的方程来描述。
双曲线的特征在于它有两个焦点,它们分别是双曲线的两个顶点。
由于双曲线有两个焦点,因此它也有两个极点,它们是双曲线离这两个焦点最近的两个点。
因此,双曲线具有将曲线联系起来的两个重要特征,它们是焦点和极点。
此外,双曲线也有几何学中很重要的特征,比如其圆心角,两极点夹角以及两焦点的距离等等。
这些特征都可以由它在y轴上的标准方程表达出来,比如说圆心角就可以由如下方程表示:$$angle j = arctan left( frac { 2b } { a } right) $$ 此外,双曲线也有椭圆的特征,椭圆是几何学中一种特殊的双曲线,它的形状与椭圆形极为接近,可以用如下方程表示出来:$$frac { { x }^{ 2 } }{ { a }^{ 2 } }+frac{ { y }^{ 2 } }{ { b }^{ 2 } }=1$$由于双曲线具有许多重要的理论特征,因此双曲线在几何学中具有重要的意义。
双曲线定义、标准方程
一. 教学内容:
双曲线定义、标准方程
(一)双曲线的定义
1. (1)图示:取一拉链,在拉开两边上各选一点,分别固定在F1、F2上,|F1F2|=2c,即|PF1|-|PF2|=2a,得到的图形,我们称为双曲线一支(加绝对值两支)
3. 定义:平面内与两定点F1、F2的距离之差的绝对值等于常数c小于|F1F2|的点的轨迹叫双曲线。
(1)焦点:F1、F2,焦距:|F1F2|
(2)定义重点:
①绝对值
②小于|F1F2|
若去掉①则为一支;去掉②,2a=2c射线,2a>2c无曲线,2a=0是F1F2的中垂线。
(二)双曲线的标准方程
(1)推导:①建系;②写出集合;③坐标化;④化简
图象特征:
[注意]
1. 位于标准位置,才能有标准方程;
3. 判断双曲线焦点的位置由函数的正负决定(不比大小),若x2的函数为正,则焦点在x轴上,反之则在y轴上。
4. 记住a、b、c的关系:
一般地:第二定义:平面内与一个定点的距离和它到一条定直线的距离的比是常数
线叫做双曲线的准线,这个常数e叫做离心率。
理解:
①第二定义的隐含条件:定点在直线外,否则轨迹是除去交点的两条相交直线。
③双曲线的离心率的定义是:双曲线上一点到焦点的距离与到相应准线的距离的比。
(几何意义)
2. 焦半径及焦半径公式
定义:双曲线上一点到焦点的距离叫做双曲线上这点的焦半径。
(4)等轴双曲线:
渐近线:(定义:若曲线上的点到某一直线的距离为d,当点趋向于无穷远时,d能趋近于0,则这条直线称为该曲线的渐近线)
【典型例题】
例1. 一炮弹在某处爆炸,在F1(-5000,0)处听到爆炸声的时间比在F2(5000,0)
么样的曲线上,并求爆炸点所在的曲线方程。
解:6000(米),因此爆炸点在以F1、F2为焦点的双曲线上。
因为爆炸点离F1处比F2处更远,所以爆炸点应在靠近F2处的一支上。
设爆炸点P的坐标为(x,y),则
小结:
远6000米,这是解应用题的第一关——审题关;根据审题结合数学知识知爆炸点所在的曲线是双曲线,这是解应用题的第二关——文化关(用数学文化反映实际问题);借助双曲线的标准方程写出爆炸点的轨迹方程是解决应用题的第三关——数学关(用数学知识解决第二关提出的问题)。
例2. 求一条渐近线方程是3x+4y=0,一个焦点是(4,0)的双曲线标准方程,并求双曲线的离心率。
例3. 等轴双曲线的两个顶点分别为A1、A2,垂直于双曲线实轴的直线与双曲线交于M、N两点,求证:
(1)∠MA1N+∠MA2N=180°;
(2)MA1⊥A2N,MA2⊥A1N。
小结:利用对称性把要证等式转化为证明∠NA2x+∠NA1x=90°为本题证明的突破口,体现转化意识。