2位16进制数转换2位10进制数.
- 格式:ppt
- 大小:1.19 MB
- 文档页数:38

js16进制转10进制公式摘要:1.16 进制转10 进制的公式和方法2.公式的推导过程3.实际例子和计算过程4.总结正文:一、16 进制转10 进制的公式和方法在计算机科学中,进制转换是很常见的操作。
当我们需要将16 进制的数字转换为10 进制时,可以使用以下公式:十进制数字= 16 进制数字×16 的n 次方其中,n 表示16 进制数字的位置,从右往左计数,右侧为n=0 的位置。
例如,对于16 进制数2A,我们需要将其转换为10 进制数。
首先,我们需要知道2A 在16 进制中的位置,A 的位置是1,2 的位置是2。
然后,我们使用公式计算:十进制数字= 2 ×16 的1 次方+ 10 ×16 的2 次方十进制数字= 2 ×16 + 10 ×256十进制数字= 32 + 2560十进制数字= 2592所以,16 进制数2A 转换为10 进制数是2592。
二、公式的推导过程为了更好地理解这个公式,我们可以通过数学推导来证明它。
假设我们有一个16 进制数:abcdef我们将其转换为10 进制数,可以表示为:十进制数字= a ×16 的5 次方+ b ×16 的4 次方+ c ×16 的3 次方+ d ×16 的2 次方+ e ×16 的1 次方+ f ×16 的0 次方这个公式的推导过程比较简单,主要是根据进制的定义,将16 进制的每一位乘以16 的相应次方,然后求和。
三、实际例子和计算过程以16 进制数2A 为例,我们按照公式进行计算:十进制数字= 2 ×16 的1 次方+ 10 ×16 的2 次方十进制数字= 2 ×16 + 10 ×256十进制数字= 32 + 2560十进制数字= 2592可以看到,计算结果与我们之前的例子一致。
四、总结通过以上推导和实际例子,我们可以确认16 进制转10 进制的公式和方法是正确的。

二级制转为十进制例:二级制110转化十进制(110)2=1*2^2+1*2^1+0*2^0即二级制从右边起第一位为2^0,第二位为2^1,第三位为2^3,第四位为2^4……十进制转化为二进制商为0,于是结果为余数的倒排列即为(37)10=(a5a4a3a2a1a0)2=(100101)2十六进制转为二进制,二进制转为十六进制(二进制和十六进制的互相转换比较重要。
不过这二者的转换却不用计算,每个C,C++程序员都能做到看见二进制数,直接就能转换为十六进制数,反之亦然。
)十六进制转为二进制:每一位十六进制数对应二进制的四位,逐位展开。
二进制数转为十六进制:将二进制数转换成十六进制数是将二进数的整数部分从右向左每四位一组,每一组为一位十六进制整数,不足四位时,在前面补0<(FB)16=(1111 ,1011)2 可以互转>二进制与十六进制的关系:可以用四位数的二进制数来代表一个16进制,如3A16 转为二进制为: 3为0011,A 为1010,合并起来为00111010。
可以将最左边的0去掉得1110102若要将二进制转为16进制,只需将二进制的位数由右向左每四位一个单位分隔,将各单位对照出16进制的值即可。
16进制数转换为10进制数:假设有一个十六进数 2AF5, 那么如何换算成10进制呢?用竖式计算: 2AF5换算成10进制:直接计算就是:5 * 16^0 + F * 16^1 + A * 16^2 + 2 * 16^3 = 10997(别忘了,在上面的计算中,A表示10,而F表示15)假设有人问你,十进数 1234 为什么是一千二百三十四?你尽可以给他这么一个算式: 1234 = 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0 如十进制数2039它可以表示为:2*10^3+0*10^2+3*10^1+9*10^0那么任何进制的数都一样,例如16进制数8A30E它就是8*16^4+10*16^3+3*16^2+0*16^1+14*16^0=566030,算出来的值就是这个数对应的十进制数又例如k进制数abcdef(这是一个6位数)它就是a*k^5+b*k^4+c*k^3+d*k^2+e*k^1+f*k^016进制数转换为10进制数:与10进制整理转换成2进制类似,只是把除数改为16 除16取余例如57除数不够16除即停止57∕16 = 3……9 (57除16等于3余9)所以结果为39H (H代表十六进制)。
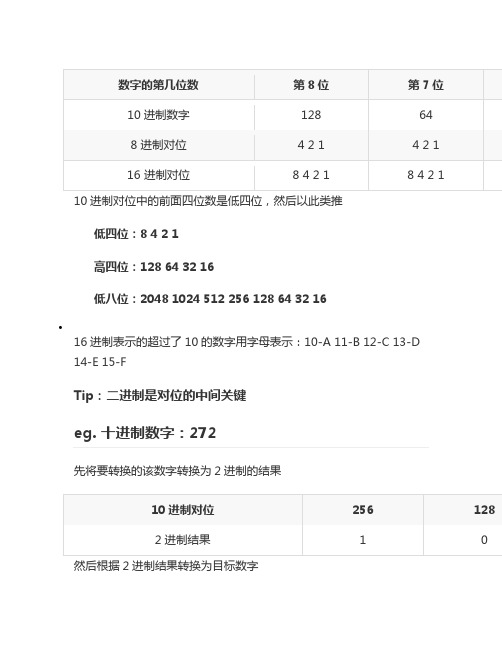
数字的第几位数第8位第7位
10进制数字128 64
8 进制对位 4 2 1 4 2 1
16 进制对位8 4 2 1 8 4 2 1
10进制对位中的前面四位数是低四位,然后以此类推
低四位:8 4 2 1
高四位:128 64 32 16
低八位:2048 1024 512 256 128 64 32 16
16进制表示的超过了10的数字用字母表示:10-A 11-B 12-C 13-D 14-E 15-F
Tip:二进制是对位的中间关键
eg. 十进制数字:272
先将要转换的该数字转换为2进制的结果
eg. 十进制数字:147
eg. 16进制数字:F7
逻辑运算符
& 与运算:同 1 为 1 ,否则为 0
| 或运算:有 1 为 1,否则为 0
1 ,否则为 0
左移运算:按照2进制向左移动两位
右移运算:按照2进制向右移动两位
Q :272 & 147
A : 16(结果是换算成了二进制之后进行的计算)Q :272 | 147
A :403
Q :272 ^ 147
A :387
Q :35>>2
A :8
Q :35<<2
A :140
二进制的最高位定义为符号位,最高位表示负数。
机器数:连同符号位一起数值化了的值
真值:机器数代表的真实的数值
数值位:真值的绝对值
正数二进制,原码、补码、反码都是同一个
负数二进制,补码=反码+1。

十进制数与十六进制数的转换在计算机科学和数学领域,我们经常需要进行数字的进制转换。
其中,最常见的是十进制数与十六进制数之间的转换。
本文将介绍如何准确、简便地进行这种转换。
一、十进制转十六进制1. 整数部分转换:十进制数的整数部分转换为十六进制时,采用除以16的方法。
将十进制数不断除以16,直到商为0为止,将每次的余数按照从后向前的顺序排列,就得到了十六进制的表示。
例如,将十进制数255转换为十六进制:(1)255 ÷ 16 = 15 余 15,余数为F,代表十六进制中的15;(2)15 ÷ 16 = 0 余 15,余数依然为F。
因此,255的十六进制表示为FF。
2. 小数部分转换:十进制数的小数部分转换为十六进制时,采用乘以16的方法。
将十进制数的小数部分与16相乘,取整数部分作为十六进制数的一位,再将小数部分与16再相乘,继续取整数部分作为十六进制数的下一位,直到小数部分为0或达到所需精度。
例如,将0.625转换为十六进制:(1)0.625 × 16 = 10,十六进制中的10表示为A,因此0.625的十六进制表示为0.6A。
二、十六进制转十进制1. 整数部分转换:十六进制数的整数部分转换为十进制时,采用乘以相应权重的方法。
将十六进制数的每一位分别与16的相应次方相乘,再将每一位的结果相加,即可得到十进制数的表示。
例如,将十六进制数A7转换为十进制:A7 = 10 × 16^1 + 7 × 16^0 = 160 + 7 = 167。
2. 小数部分转换:十六进制数的小数部分转换为十进制时,采用乘以相应的负幂次的方法。
将十六进制数的每一位分别与16的相应负幂次相乘,再将每一位的结果相加,即可得到十进制数的表示。
例如,将十六进制数0.6A转换为十进制:0.6A = 6 × 16^(-1) + 10 × 16^(-2) = 0.375 + 0.0390625 = 0.4140625。

十进制数与十六进制数的转换方法
1.十进制数转换为十六进制数:
十进制数是我们日常使用的数制系统,由0~9这10个数字组成。
而
十六进制数是一种16进制的数制系统,由0~9和A~F这16个字符组成。
转换步骤如下:
(1)将十进制数除以16,得到商和余数;
(2)余数即是十六进制数的最低位数;
(3)将商再除以16,得到新的商和余数,余数即是十六进制数的第
二位数;
(4)依次类推,直到商为0为止;
(5)最终的十六进制数就是将所有的余数倒序排列而成。
例如,将十进制数100转换为十六进制数:
(1)100÷16=6,余数为4,此时十六进制数的最低位数为4;
(2)6÷16=0,余数为6,此时十六进制数的第二位数为6;
(3)最终的十六进制数为64
2.十六进制数转换为十进制数:
转换步骤如下:
(1)按权展开法,将每一位的十六进制数乘以相应的权值,再求和;
(2)权值由低到高依次为16^0,16^1,16^2,...;
(3)将每一位的十六进制数转换为对应的十进制数;
(4)将所有十进制数相加,得到最终的结果。
例如,将十六进制数A5转换为十进制数:
(1)A的十进制数值为10,所以A5的第一位数为10×16^1=160;
(2)5的十进制数值为5,所以A5的第二位数为5×16^0=5;
(3)最终的十进制数为160+5=165
以上就是十进制数与十六进制数之间的转换方法。
根据上述方法,我们可以将一个数从十进制转换为十六进制,或者将一个数从十六进制转换为十进制。
这些转换方法在计算机科学、数学等领域中经常被使用。

八、十六进制数转换到十进制数6.2.1二进制数转换为十进制数二进制数第0位的权值是2的0次方,第1位的权值是2的1次方…所以,设有一个二进制数:01100100,转换为10进制为:下面是竖式:01100100换算成十进制第0位0*20=0第1位0*21=0第2位1*22=4第3位0*23=0第4位0*24=0第5位1*25=32第6位1*26=64第7位0*27=0+---100用横式计算为:0*20+0*21+1*22+1*23+0*24+1*25+1*26+0*27=1000乘以多少都是0,所以我们也可以直接跳过值为0的位:1*22+1*23+1*25+1*26=1006.2.2八进制数转换为十进制数八进制就是逢8进1。
八进制数采用0~7这八数来表达一个数。
八进制数第0位的权值为8的0次方,第1位权值为8的1次方,第2位权值为8的2次方…所以,设有一个八进制数:1507,转换为十进制为:用竖式表示:1507换算成十进制。
第0位7*80=7第1位0*81=0第2位5*82=320第3位1*83=512+--839同样,我们也可以用横式直接计算:7*80+0*81+5*82+1*83=839结果是,八进制数1507转换成十进制数为8396.2.3八进制数的表达方法C,C++语言中,如何表达一个八进制数呢?如果这个数是876,我们可以断定它不是八进制数,因为八进制数中不可能出7以上的阿拉伯数字。
但如果这个数是123、是567,或12345670,那么它是八进制数还是10进制数,都有可能。
所以,C,C++规定,一个数如果要指明它采用八进制,必须在它前面加上一个0,如:123是十进制,但0123则表示采用八进制。
这就是八进制数在C、C++中的表达方法。
由于C和C++都没有提供二进制数的表达方法,所以,这里所学的八进制是我们学习的,CtC++语言的数值表达的第二种进制法。
现在,对于同样一个数,比如是100,我们在代码中可以用平常的10进制表达,例如在变量初始化时:inta=100;我们也可以这样写:inta=0144;//0144是八进制的100;一个10进制数如何转成8进制,我们后面会学到。
16进制转10进制计算方法16进制转10进制计算方法概述在计算机科学中,16进制(Hexadecimal)是一种常用的进制表示方法。
它使用了0-9的数字和A-F的字母表示数值,其中A代表10,B代表11,以此类推。
当需要将16进制数转换为10进制数时,有几种计算方法可以使用。
方法一:逐位计算法1.将16进制数的每一位数值与其对应的权重相乘。
2.将每一位的结果相加,即可得到10进制数值。
例子:要将16进制数”3A”转换为10进制数。
- 首先,将3与16的1次方相乘,得到48。
- 其次,将A(十六进制的10)与16的0次方相乘,得到10。
- 最后,将48和10相加,得到58。
因此,“3A”的十进制表示为58。
方法二:幂运算法1.从16进制数的最后一位(个位)开始,遍历到第一位(最高位)。
2.对每一位的数值进行幂运算,乘以对应的权重。
3.将所有结果相加,即可得到最终的10进制数值。
例子:要将16进制数”3A”转换为10进制数。
- 首先,对A (十六进制的10)进行幂运算,乘以16的0次方,得到10。
- 其次,对3进行幂运算,乘以16的1次方,得到48。
- 最后,将10和48相加,得到58。
因此,“3A”的十进制表示为58。
方法三:利用公式转换对于一个n位的16进制数,可以使用以下公式将其转换为10进制数:十进制数值 = d<sub>n-1</sub> * 16<sup>n-1</sup> + d< sub>n-2</sub> * 16<sup>n-2</sup> + ... + d<sub>1</sub> * 16<sup>1</sup> + d<sub>0</sub> * 16<sup>0</sup>其中,dn-1到d0为16进制数的每一位数值,n为16进制数的位数。
十进制和十六进制是计算机中常见的数制。
在计算机中,数据存储和处理都是以二进制的形式进行的,而在实际的编程中,为了方便人类阅读和书写代码,常常使用十进制和十六进制进行表示。
了解十进制和十六进制之间的转换方法对于理解计算机编程及相关知识至关重要。
一、十进制和十六进制的定义和特点1. 十进制定义:十进制是我们日常生活中常用的数制,有0-9十个数字,每一位的权值是10的幂次方。
2. 十六进制定义:十六进制是一种使用16个数字(0-9以及A-F)来表示数字的数制,每一位的权值是16的幂次方。
二、十进制向十六进制的转换方法1. 整数部分转换:将十进制整数部分不断除以16,将余数写下来,直至商为0为止,然后将余数倒过来即为对应的十六进制数。
示例:将十进制数2348转换为十六进制步骤一:2348 ÷ 16 = 146……12(C)步骤二:146 ÷ 16 = 9 (2)步骤三:9 ÷ 16 = 0 (9)所以2348的十六进制为92C。
2. 小数部分转换:将十进制小数部分乘以16,将得到的整数部分作为十六进制的位,将小数部分乘16再取整,直至小数部分为0或者达到要求的精度。
例如:0.625 转换为十六进制的结果为0.A。
三、十六进制向十进制的转换方法1. 整数部分转换:将十六进制的每一位乘以16的幂次方,然后相加即可得到对应的十进制数。
示例:将十六进制数3A7转换为十进制3A7 = 3×16^2 + 10×16^1 + 7×16^0 = 9352. 小数部分转换:将十六进制小数部分转化为十进制,并且将结果除以16取余再乘16,得到的整数部分作为十进制的小数部分。
例如:0.A 转化为十进制的结果为0.625。
四、注意事项与常见问题1. 在进行十进制和十六进制的转换过程中需要小心保持数字的准确性,一旦出现计算错误可能会导致结果的失真。
2. 在实际编程中,经常会涉及到各种进制的转换,因此掌握进制转换的方法是非常重要的。
16进制转化为10进制的方法16进制转换为10进制的方法在计算机科学中,十进制(Decimal)和十六进制(Hexadecimal)是常见的数字系统。
在日常生活和计算机中,我们常使用十进制数字系统。
然而,在计算机科学和编程领域,十六进制也是非常重要的。
因此,了解如何将十六进制数转换为十进制数是非常有用的。
本文将详细介绍如何将16进制转换为10进制的方法,以及具体的步骤和示例。
一、理解十进制和十六进制在开始转换之前,我们首先需要了解十进制和十六进制之间的差异。
十进制是一种基于10个数字(0-9)的数字系统。
它的位置权重递增,从右到左,每个位置上的权重是10的幂(10^0, 10^1, 10^2, ...)。
例如,数字512的意思是5 * 10^2 + 1 * 10^1 + 2 * 10^0。
十六进制是一种基于16个数字(0-9, A-F)的数字系统。
它的位置权重递增,从右到左,每个位置上的权重是16的幂(16^0, 16^1, 16^2, ...)。
例如,十六进制数5A的意思是5 * 16^1 + 10 * 16^0。
二、将16进制转换为10进制的步骤下面是将16进制数转换为10进制数的步骤:步骤1:将16进制数的每个数字与其相应的权重相乘。
步骤2:将步骤1中的结果相加。
让我们通过一个示例来演示这个过程。
示例:将十六进制数3E7转换为十进制数。
步骤1:将16进制数的每个数字与其相应的权重相乘。
3E7 = 3 * 16^2 + E * 16^1 + 7 * 16^0步骤2:将步骤1中的结果相加。
3 * 16^2 + 14 * 16^1 + 7 * 16^0 = 768 + 224 + 7 = 999因此,十六进制数3E7等于十进制数999。
三、其他注意事项1. 当遇到十六进制数的字母A、B、C、D、E和F时,分别对应十进制数10、11、12、13、14和15。
例如,十六进制数4A2F转换为十进制数的步骤如下:4A2F = 4 * 16^3 + 10 * 16^2 + 2 * 16^1 + 15 * 16^0= 16384 + 40960 + 32 + 15= 573912. 使用计算器或编程语言来实现转换更加简便。