初中数学经典习题资料

初中数学经典试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是偶数？A. 3B. 5C. 8D. 72. 如果一个数的相反数是它本身，那么这个数是：A. 0B. 1C. -1D. 23. 一个数的绝对值是它本身，那么这个数是：A. 正数B. 负数C. 非负数D. 非正数4. 计算下列算式的结果：(2x - 3) + (3x + 4) =A. 5x + 1B. 5x - 1C. 2x + 1D. 2x - 15. 下列哪个选项是方程的解？A. x + 2 = 5，x = 3B. x - 2 = 5，x = 3C. 2x + 3 = 7，x = 2D. 3x - 4 = 5，x = 36. 一个三角形的三个内角之和是：A. 90°B. 180°C. 360°D. 270°7. 一个圆的直径是10厘米，那么它的半径是：A. 5厘米B. 10厘米C. 20厘米D. 15厘米8. 下列哪个选项是不等式的解集？A. x > 5B. x < 5C. x = 5D. x ≠ 59. 一个数的立方是它本身，那么这个数是：A. 0B. 1C. -1D. 以上都是10. 一个数的平方等于它本身，那么这个数是：A. 0B. 1C. -1D. 以上都是二、填空题（每题4分，共20分）11. 一个数的平方根是它本身，那么这个数可以是______。

12. 如果一个数的绝对值是5，那么这个数可以是______。

13. 一个数的倒数是它本身，那么这个数是______。

14. 一个数的相反数是它本身，那么这个数是______。

15. 一个数的立方等于它本身，那么这个数可以是______。

三、解答题（每题5分，共50分）16. 解方程：2x - 5 = 9。

17. 计算：(3x + 2)(2x - 3)。

18. 证明：在一个直角三角形中，斜边的平方等于两直角边的平方和。

数学初中经典试题及答案一、选择题（每题3分，共30分）1. 已知一个数的平方等于36，这个数可能是：A. 6B. -6C. 6或-6D. 以上都不是2. 一个三角形的两边长分别为3和5，第三边长为：A. 2B. 4C. 6D. 83. 计算下列表达式的值：\((-3) \times (-2)\)A. 6B. -6C. 3D. -34. 一个圆的半径为5厘米，那么它的面积是：A. 78.5平方厘米B. 25平方厘米C. 78.5平方分米D. 25平方分米5. 以下哪个是等腰三角形？A. 三边长分别为3, 4, 5B. 三边长分别为5, 5, 5C. 三边长分别为2, 3, 4D. 三边长分别为1, 2, 36. 一个数的绝对值是5，这个数可能是：A. 5B. -5C. 5或-5D. 以上都不是7. 计算下列表达式的值：\((-2)^2\)A. 4B. -4C. 2D. -28. 一个直角三角形的两条直角边长分别为6和8，那么斜边长为：A. 10B. 14C. 16D. 209. 一个数的立方等于-64，这个数是：A. 4B. -4C. 2D. -210. 计算下列表达式的值：\((-1)^3\)A. 1B. -1C. 3D. -3二、填空题（每题2分，共20分）1. 一个数的相反数是-7，这个数是________。

2. 一个数的倒数是\(\frac{1}{3}\)，这个数是________。

3. 一个数的平方根是4，这个数是________。

4. 一个数的立方根是2，这个数是________。

5. 一个等差数列的首项是2，公差是3，那么第5项是________。

6. 一个等比数列的首项是3，公比是2，那么第3项是________。

7. 一个直角三角形的斜边长是10，一个直角边长是6，那么另一个直角边长是________。

8. 一个圆的直径是10厘米，那么它的周长是________厘米。

9. 一个数的绝对值是8，这个数是________或________。

初中数学解方程经典练习题及答案解下列方程：1、2（4+x ）-6x= 0.7（x-2）；2、2+x 3 =3.5- 7−x 2；3、x = 1+ x 3 + x 6 + x 12 + x 24；4、4x +5x +6x = 16（16x +20x +24x ）；5、（3x −8）3 + x 3 + 60x =120；6、（2x −5）3 + （2x −6）2=3；7、（x −1）3+（x −3）3 =2（x −2）2 +6；8、 x 2 +1=√x （x+1）；9、（x -5555）（x -5562）=8；10、3·3x +33·3−x =82参考答案1、2（4+x ）-6x= 0.7（x-2）；解：2（4+x ）-6x= 0.7（x-2）8+2x-6x=0.7x-1.4（2-6-.07）x= -1.4-8-4.7x=-9.4x=2故原方程的解是：x=22、2+x 3=3.5- 7−x 2 解：2+x 3 =3.5- 7−x 2 去分母，两边同时乘以6，得2（2+x ）=6×3.5-3（7-x ）4+2x=21-21+3xx=4故原方程的解是：x=43、x = 1+ x 3 + x 6 + x 12 + x 24； 解：x = 1+ x 3 + x 6 + x 12 + x 24去分母，两边同时乘以24，得24x=24 +8x +4x +2x +x（24-8-4-2-1）x =249x=24x= 83故原方程的解是：x= 834、4x+5x+6x= 16（16x+20x+24x）；解：4x+5x+6x= 16（16x+20x+24x）=16〔（4×4）x+ （4×5）x+ （4×6）x〕=16（4x×4x+4x×5x+4x×6x）=16×4x（4x+5x+6x）因为4x+5x+6x≠0，所以等号两边同时除以4x+5x+6x，得1=16×4x=42×4x=4x+2又1=40所以：4x+2=40故：x+2=0解得：x=-2故原方程的解是：x=-25、（3x−8）3+ x3+ 60x =120解：（3x−8）3+ x3+ 128= 64x前面两项运用立方和公式，后面两项结合在一起，得〔（3x-8）+x〕〔（3x−8）2- x（3x-8）+ x2〕+（128-64x）=0（4x-8）（7 x2-40x +64）-16（4x+8）=0提取公因式（4x-8），得（4x-8）（7 x2-40x +64-16）=0（4x-8）（7 x2-40x +48）=0（4x-8）（7x-12）（x-4）=0由4x-8=0，解得x=2由7x-12=0，解得x= 127由x-4=0，解得x=4故原方程的解是：x=2，x= 12，x=476、（2x−5）3+ （2x−6）2=3；解：令2x-5=t, 2x-6=t-1则原式变为t3+ （t−1）2=3t3+ t2-2t +1=3t3+ t2-2t -2=0前两项结合，后两项结合，得（t3+ t2）+（-2t -2）=0t2（t+1）-2（t+1）=0（t+ 1）（t2-2）=0则t= -1或t = ±√2（1）当t= -1即：2x-5= -1解得：x=2（2）当t = ±√2即：2x-5=±√2解得：x= 5±√22故原方程的解是：x= 5±√227、（x−1）3+（x−3）3=2（x−2）2+6解：设x -2=t则原式为（t +1）3+（t −1）3=2 t2+6t3+3 t2+3t +1 + t3-3 t2+3t -1 =2 t2+6 2 t3+6t=2 t2+6整理，得t3 - t2 +3t -3=0前两项结合，后两项结合，得（ t3 - t2）+（3t -3）=0 t2（t -1）+3（t-1）=0 （t -1）（ t2+3）=0因为 t2+3 ≠0只有t -1=0所以t= 1又x -2=t即：x -2=1解得：x=3故原方程的解是：x=38、 x2+1=√x（x+1）；解：x2+1=√x（x+1）x2+1=x√x +√xx2 +1 -x√x -√x =0设√x=tt4+1 - t3− t=0（ t4- t3）+（1− t）=0 t3（t−1）−（t−1）=0（t−1）（ t3−1）=0则有t−1=0或 t3−1=0（1）当t−1=0t= 1又√x=t所以x=1（2）当 t3−1=0t3=1解得t=1又√x=t所以x=1故原方程的解是：x=19、（x -5555）（x -5562）=8；解：令x-5555=t则x-5562=t-7原方程（x-5555）（x-5562）=8t（t -7）=8t2 -7t -8=0（t -1）（t+8）=0则有t -1=0或t+8=0（1）当t -1=0t=1又x-5555=t即：x-5555=1解得：x=5556（2）当t +8=0t= -8又x-5555=t即：x-5555= -8解得：x=5547故原方程的解是：x=5556，x=554710、3·3x +33·3−x=82解：3·3x +33·3−x=82两边同时乘以3x，得3·（3x）2 +33=82·3x令3x=t，则3t2 +27 -82t=0（3t -1）（t-27）=0则：3t -1=0或t-27=0（1）当3t -1=0即：t = 13又3x=t所以：3x= 133x=3−1解得：x= -1（1）当t -27=0即：t =27又3x=t所以：3x= 273x=33解得：x= 3故原方程的解是：x= -1，x= 3。

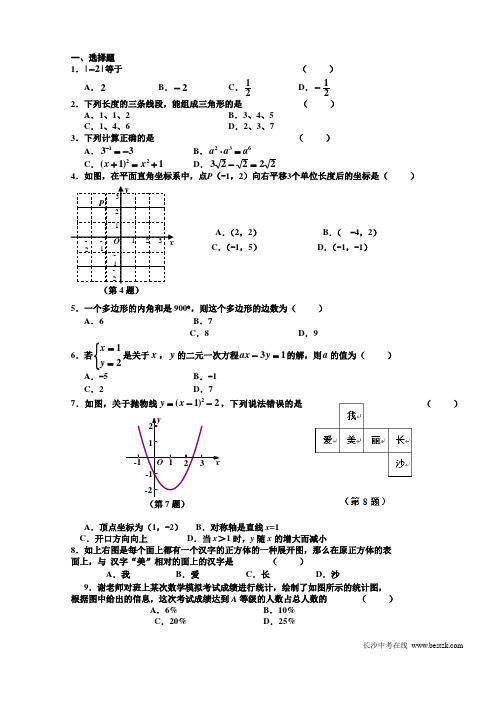
232-2-11-11O x y （第7题） （第4题）O xP · 121-1 1y -1 1-2 22-2 23 3一、选择题1．|2|-等于 （ ） A ．2B ．2-C ．21D ．21-2．下列长度的三条线段，能组成三角形的是 （ ） A ．1、1、2 B ．3、4、5C ．1、4、6D ．2、3、73．下列计算正确的是 （ ）A ．331-=-B ．632a a a =⋅C ．1)1(22+=+x xD ．22223=-4．如图，在平面直角坐标系中，点P （-1，2）向右平移3个单位长度后的坐标是（ ）A ．（2，2）B ．（ -4，2）C ．（-1，5）D ．（-1，-1）5．一个多边形的内角和是900︒，则这个多边形的边数为（ ）A ．6B ．7C ．8D ．96．若⎩⎨⎧==21y x 是关于x ，y 的二元一次方程13=-y ax 的解，则a 的值为（ ）A ．-5B ．-1C ．2D ．77．如图，关于抛物线2)1(2--=x y ，下列说法错误的是（ ）A ．顶点坐标为（1，-2）B ．对称轴是直线x =1C ．开口方向向上D ．当x ＞1时，y 随x 的增大而减小8．如上右图是每个面上都有一个汉字的正方体的一种展开图，那么在原正方体的表 面上，与 汉字“美”相对的面上的汉字是 （ ）A ．我B ．爱C ．长D ．沙9．谢老师对班上某次数学模拟考试成绩进行统计，绘制了如图所示的统计图， 根据图中给出的信息，这次考试成绩达到A 等级的人数占总人数的 （ ） A ．6% B ．10% C ．20% D ．25%DA BC （第10题）AB EC D10．如图，等腰梯形ABCD 中，AD ∥BC ，∠B =45︒，AD =2，BC =4，则梯形的面积为A ．3B ．4C ．6D ．8二、填空题 11．分解因式：22b a -= ．12．反比例函数xky =的图象经过点A （-2，3），则k 的值为 ．13．如图，CD 是△ABC 的外角∠ACE 的平分线，AB ∥CD ，∠ACE =100︒，则∠A = ︒．14. 化简：xx x 11-+= ．（第13题）15．在某批次的100件产品中，有3件是不合格产品，从中任意抽取一件检验，则抽到不合 格产品的概率是 ．16．菱形的两条对角线的长分别是6cm 和8cm ，则菱形的周长是 cm ．17．已知33=-b a ，则b a 38+-的值是 ．18．如图，P 是⊙O 的直径AB 延长线上的一点，PC 与⊙O 相切于点C ，若∠P =20︒， 则∠A = ︒．PCAO B （第18题）三、解答题19．已知a =9，b =20110，c =)2(--，求c b a +-的值．PD CB OA20．解不等式)2(2-x ≤x 36-，并写出它的正整数解．21．“珍惜能源从我做起，节约用电人人有责”．为了解某小区居民节约用电情况，物业公司随 机抽取了今年某一天本小区10户居民的日用电量，数据如下：用户序号12 3 4 5 6 7 8 9 10 日用电量（度） 4.4 4.05.05.63.44.83.45.24.04.2（1）求这组数据的极差和平均数；（2）已知去年同一天这10户居民的平均日用电量为7.8度，请你估计，这天与去年同日相 比，该小区200户居民这一天共节约了多少度电？22．如图，在⊙O 中，直径AB 与弦CD 相交于点P ，∠CAB =40︒，∠APD =65︒．（第22题）（1）求∠B 的大小； （2）已知圆心O 到BD 的距离为3，求AD 的长．23．某工程队承包了某标段全长1755米的过江隧道施工任务， 甲、乙两个班组分别从东、西两端同时掘进．已知甲组比乙组 平均每天多掘进0.6米，经过5天施工，两组共掘进了45米．（1）求甲、乙两个班组平均每天各掘进多少米？（2）为加快工程进度，通过改进施工技术，在剩余的工程中，甲组平均每天能比原来多 掘进0.2米，乙组平均每天能比原来多掘进0.3米．按此施工进度，能够比原来少用多少 天完成任务？24．如图是一座人行天桥的引桥部分的示意图，上桥通道由两段互相平行并且与地面成37︒角 的楼梯AD 、BE 和一段水平平台DE 构成．已知天桥高度BC =4.8米，引桥水平跨度AC =8米．（1）求水平平台DE 的长度；（2）若与地面垂直的平台立柱MN 的高度为3米，xy QB A OP. .N MEA BCD37︒ 求两段楼梯AD 与BE 的长度之比．（参考数据：取sin37︒=0.60，cos37︒=0.80，tan37︒=0.75）（第24题） 25．使得函数值为零的自变量的值称为函数的零点．例如，对于函数1-=x y ，令0=y ， 可得1=x ，我们就说1是函数1-=x y 的零点． 已知函数)3(222+--=m mx x y （m 为常数）． （1）当m =0时，求该函数的零点；（2）证明：无论m 取何值，该函数总有两个零点； （3）设函数的两个零点分别为1x 和2x ，且411121-=+x x ，此时函数图象与x 轴的交点分 （4）别为A 、B （点A 在点B 左侧），点M 在直线10-=x y 上，当MA +MB 最小时，（5）求直线AM 的函数解析式．26．如图，在平面直角坐标系中，已知点A （0，2），点P 是x 轴上一动点，以线段AP 为一 边，在其一侧作等边三角形APQ ．当点P 运动到原点O 处时，记Q 的位置为B ．（1）求点B的坐标；（2）求证：当点P 在x 轴上运动（P 不与O 重合）时，∠ABQ 为定值；（3）是否存在点P ，使得以A 、O 、Q 、B 为顶点的四边形是梯形？若存在，请求出P 点 的坐标；若不存在，请说明理由．（第26题）2011年长沙市初中毕业学业水平考试试卷数学参考答案及评分标准一、选择题（本题共10个小题，每小题3分，共30分）题号 1 2 3 4 5 6 7 8 91 0答案 A B D A B D D C C A1、A2、B3、D4、A5、B6、D7、D8、C９、C10、A二、填空题（本题共8个小题，每小题3分，共24分）11．))((b a b a -+12．-613．5014．115．0.0316．2017．518．35三、解答题（本题共2个小题，每小题6分，共12分）19．∵a =9=3，b =20110=1，c =)2(--=2， …………………………… 4分∴c b a +-＝3-1+2=4. ………………………………………………… 6分20．原不等式)2(2-x ≤x 36-可化为42-x ≤x 36-， ………………1分 即5x ≤10， ………………………………………………………… 3分 解得x ≤2. …………………………………………………………4分 ∴不等式的正整数解为1和2. ………………………………………6分四、解答题（本题共2个小题，每小题8分，共16分） 21. （1）极差：5.6－3.4=2.2（度）；……………………………………… 2分平均数：(4.4+4.0+5.0+5.6+3.4+4.8+3.4+5.2+4.0+4.2)÷10=4.4（度）.… 4分 （2）这10户居民这一天平均每户节约：7.8－4.4=3.4（度）， ……… 6分由此估计整个小区居民这一天平均每户节约3.4度，所以该小区200户居民这一天共节约 3.4×200=680（度）.……………… 8分22．（1）∵∠APD 是△APC 的外角，∴∠APD =∠CAP +∠C ，……………… 1分 即65︒=40︒+∠C ， ∴∠C =25︒……………………… 2分∴∠B =∠C =25︒. ……………………… 4分 （2）过点O 作OE ⊥BD 于E ， ……… 5分EP DCBO A根据垂径定理得 E 是BD 的中点，…… 6分 又∵O 是AB 的中点， ∴OE 是△ABD 的中位线，………………………………………………… 7分∴A D =2OE =6. ………………………………………………………………… 8分五、解答题（本题共2个小题，每小题9分，共18分）23．（1）设甲、乙两个班组平均每天分别掘进x 米、y 米，……………………… 1分依题意得⎩⎨⎧=+=-45)(56.0y x y x ……………………………………………………3分解得：⎩⎨⎧==2.48.4y x …………………………………………………………… 5分答：甲、乙两个班组平均每天分别掘进4.8米和4.2米. ………………… 6分（2）设按原来的施工进度和改进施工技术后的进度分别还需要a 天、b 天完成任务，则 a =(1755－45)÷(4.8+4.2)=190（天）， ……………………………………… 7分 b =(1755－45)÷(4.8+4.2+0.2+0.3)=180（天），…………………………… 8分∴a －b =190－180=10（天）， 答：能比原来少用10天完成任务. ……………………………………… 9分24．（1）延长BE 交AC 于F ，∵AD ∥BE ，∴AD ∥EF ，又∵DE ∥AF ，∴四边形ADEF 是平行四边形， ……………………… 1分∴DE =AF .…………………………………………………………… 2分在Rt △BFC 中，BC =4.8, ∠BFC =∠A=37︒,∵tan ∠BFC =CF BC ，∴tan 37︒=CF 8.4=0.75， ………………………………… 3分∴CF =6.4（米）. …………………………………………………………… 4分 AF =AC －CF =8－6.4=1.6（米）， ∴DE =1.6（米）.………………………………………………… 5分（2）过点E 作EG ⊥AC 于G ，37°G FN MEABCD∵MN ⊥AC ，DE ∥AC ，∴EG=MN=3（米）， …………… 6分 又∵BC ⊥AC ，EG ⊥AC ，∴EG ∥BC ∴△FEG ∽△FBC ，∴BF EF =BC EG =8.43，∴BFEF=85，∴BEEF=35, ………………… 8分由（1）知，四边形ADEF 是平行四边形，AD =EF ， ∴AD :BE =5:3. …………………………………………………………… 9分六、解答题（本题共2个小题，每小题10分，共20分）25．（1）当0=m 时，62-=x y ， …………………………………… 1分令0=y ，即062=-x ，解得6±=x ， ……………………… 2分∴当0=m 时，该函数的零点为6和－6. ……………………… 3分 （2）令0=y ，即0)3(222=+--m mx x ， ……………………… 4分△=(－2m )2－4[－2(m +3)]=4m 2+8m +24=4(m +1)2+20 ……………………………………… 5分∵无论m 为何值，4(m +1)2≥0，4(m +1)2+20＞0，即△＞0，∴无论m 为何值，方程0)3(222=+--m mx x 总有两个不相等的实数根， 即该函数总有两个零点. ………………………………………………… 6分 （3）依题意有，m x x 221=+，)3(221+-=m x x ，由411121-=+x x 得2121x x x x ⋅+=－41， 即)3(22+-m m=－41，解得m ＝1. …………………………………………………………… 7分 因此函数解析式为y =x 2－2x －8， 令y =0，解得x 1=－2，x 2=4，∴A （－2，0），B （4，0），作点B 关于直线10-=x y 的对称点B ´，连结AB ´，MB'DCB AOxy 则AB ´与直线10-=x y 的交点就是满足条件的M 点. …………… 8分 易求得直线10-=x y 与x 轴、y 轴的交点分别为C (10，0)，D (0，－10)， 连结CB ´，则∠BCD =45︒， ∴B C =CB ´=6，∠B´CD =∠BCD =45︒， ∴∠BCB ´=90︒.即B´（10，-6）. ……… 9分 设直线AB ´的解析式为b kx y +=，则 ⎩⎨⎧-=+=+-61002b k b k ， 解得21-=k ，1-=b .∴直线AB ´的解析式为121--=x y ， 即AM 的解析式为121--=x y . ……………………………………… 10分26．（1）过点B 作BC ⊥y 轴于点C ， …………………………………………… 1分xyCQBA OP∵A （0，2），△AOB 为等边三角形，∴AB=OB=2，∠BAO =60︒， ∴BC =3，OC =AC =1， 即B (3，1).………………… 3分（2）当点P 在x 轴上运动（P 不与O 重合）时，不失一般性， ∵∠PAQ =∠O AB=60︒，∴∠PAO =∠QAB ，………………4分 在△APO 和△AQB 中，∵AP =AQ ，∠PAO =∠QAB ，AO =AB ，∴△APO ≌△AQB 总成立， …………………………………………… 5分∴∠ABQ =∠AOP =90︒总成立，∴点P 在x 轴上运动（P 不与O 重合）时，∠ABQ 为定值90︒. ………… 6分 （3）由（2）可知，点Q 总在过点B 且与AB 垂直的直线上， 可见AO 与BQ 不平行.………………………………………………7分①当点P 在x 轴负半轴上时，点Q 在点B 的下方， 此时，若AB ∥O Q ，四边形AOQB 即是梯形. 当AB ∥OQ 时，∠BQO=90︒，∠BOQ =∠ABO =60︒， 又OB =OA =2，可求得BQ =3， 由（2）可知△APO ≌△AQB ， ∴OP =BQ =3，xy QBAOP∴此时P 的坐标为（－3，0）. ………………………………………… 9分②当点P 在x 轴正半轴上时， 点Q 在点B 的上方，此时，若AQ ∥OB ，四边形AOBQ 即是梯形. 当AQ ∥OB 时，∠QAB =∠ABO =60°, ∠ABQ=90°，AB =2， ∴BQ =32.由（2）可知△APO ≌△AQB ， ∴OP =BQ =32，∴此时P 的坐标为（32，0）.综上，P 的坐标为（－3，0）或（32，0）. ……………………… 10分。

初中数学代数经典练习题(含答案)初中数学代数经典练题（含答案）一、线性方程组1. 某数的三分之一减去5的结果等于8，求这个数的值是多少？答案：272. 解方程组：$$\begin{align*}2x + 3y &= 7 \\3x - 4y &= 1\end{align*}$$答案：$x=5, y=-3$3. 解方程组：$$\begin{align*}2x - y &= 1 \\3x + 2y &= 14\end{align*}$$答案：$x=5, y=8$二、一元一次方程1. 解方程：$2x+1=9$答案：$x=4$2. 解方程：$5x-3=22$答案：$x=5$3. 解方程：$3(2x-1) = 15$ 答案：$x=3$三、一元二次方程1. 解方程：$x^2-3x+2=0$答案：$x=1, x=2$2. 解方程：$x^2-5x+6=0$答案：$x=2, x=3$3. 解方程：$-x^2+7x-10=0$答案：$x=2, x=5$四、等比数列1. 求等比数列的通项公式，已知首项$a=2$，公比$r=3$。

答案：$a_n = 2 \times 3^{n-1}$2. 已知等比数列的首项$a=4$，第二项$b=12$，求公比$r$。

答案：$r=3$3. 求等比数列的前$n$项和，已知首项$a=1$，公比$r=2$。

答案：$S_n = a\frac{1-r^n}{1-r}$五、函数定义1. 定义函数$f(x)=2x-3$，求$f(5)$的值。

答案：$f(5)=7$2. 定义函数$g(x)=3x^2+4$，求$g(-2)$的值。

答案：$g(-2)=16$3. 定义函数$h(x)=\frac{1}{x}$，求$h(2)$的值。

答案：$h(2)=\frac{1}{2}$以上是初中数学代数的经典练习题及其答案。

希望对你的学习有所帮助！。

初中数学解一元二次方程经典练习题（含答案）解下列解一元二次方程：1、x2=121；2、（2x+3）2=9；3、3（4x+5）2-147=0；4、（2x−7）2+9 =6（2x-7）；5、7x（x-6）=3（12-2x）；6、（3x-5）（2x+5）= x+7；7、3（3x-4）+ x（4-3x）=0；8、x（2x+5）=4（2x-1）+3；9、（x−3）2+4=5（3-x）；10、4x2+7x +1=0；11、512x2+ 13= x；12、（x−1）（x−2）2 -1 = （x+1）（x−3）3；13、14[12（x+1）+13（x+2）+2] =x2；14、（x+1）（x+2）+（x+3）（x+4）=（x+2）（x+3）+32；15、x= 2（0.3x+21）3 - （0.2x−1）（x+2）2；16、x2+（1+ 2√5）x +（ 4+√5）=0；参考答案1、x2=121；解：x2=121等式两边同时开平方x= 11故原方程的根是：x1=11，x2= -112、（2x +3）2=9；解：（2x +3）2=9等式两边同时开平方（2x +3）=±3令2x +3 = 3，即2x=0，解得x=0令2x +3 =-3，即2x=-6，解得x=-3故原方程的根是：x 1=0，x 2=-33、3（4x +5）2-147=0；解：3（4x +5）2-147=03（4x +5）2=147等式两边同时除以3（4x +5）2= 49等式两边同时开平方4x+5=±7令4x+5=7， 解得x= 12 令4x+5= -7，解得x=-3故原方程的根是：x 1= 12，x 2=-34、（2x −7）2+9 =6（2x-7）；解：（2x −7）2 +9 =6（2x-7）右边的项移到等号左边（2x−7）2-6（2x-7）+9 =0（2x−7）2 -2・3・（2x-7）+32=0[（2x−7）−3 ]2=0令（2x−7）−3 =0，解得 x=5故原方程的根是：x1=x2=55、7x（x-6）=3（12-2x）；解：7x（x-6）=3（12-2x）等号左边提取-27x（x-6）=-6（x-6）右边的项移到等号左边7x（x-6）+6（x-6）=0提取公因式（x-6）（x-6）（7x+6）=0令x-6=0，解得x=6令7x+6=0，解得x= - 67故原方程的根是：x1=6，x2=- 676、（3x-5）（2x+5）= x+7；解（3x-5）（2x+5）= x+7等号左边去括号6x2+15x-10x-25 =x+76x2+5x-25=x+76x2+4x-32=03x2+2x-16=0（3x+8）（x-2）=0令3x+8=0，解得x= - 83令x-2 =0，解得x=2故原方程的根是：x1=- 8，x2=237、3（3x-4）+ x（4-3x）=0；解：3（3x-4）+ x（4-3x）=0 3（3x-4）- x（3x-4）=0 提取公因式（3x-4）（3x-4）（3- x）=0令3x-4=0，解得x= 43令3- x =0，解得x=3，x2=3 故原方程的根是：x1= 438、x（2x+5）=4（2x-1）+3；解：x（2x+5）=4（2x-1）+3 2x2 +5x =8x-4+32x2 +5x =8x-12x2 -3x +1=0（2x-1）（x-1）=0令2x-1=0，解得x= 12 令x-1=0，解得x=1故原方程的根是：x 1= 12 ，x 2=19、（x −3）2 +4=5（3-x ）；解：（x −3）2 +4= 5（3-x ）等号左边提取-1（x −3）2 +4= -5（x-3）右边的项移到等号左边（x −3）2 +5（x-3）+4=0[（x -3）+1][（x-3）+4]=0（x-2）（x+1）=0令x-2=0，解得x=2令x+1=0，解得x=-1故原方程的根是：x 1=2，x 2=-110、4x 2+7x +1=0；解：4x 2+7x +1=0判别式△=72 -4×4×1 =33x= −7 ±√332×4 = −7 ±√338故原方程的根是：x 1=−7 +√338，x 2=−7 −√33811、512x 2 + 13 = x ； 解：512x 2 + 13 = x等式两边同时乘以125x 2 +4 =12x5x 2 +4 -12x =0（5x-2）（x-2）=0令5x-2=0，解得x= 25 令x-2=0，解得x=2故原方程的根是：x 1= 25，x 2=212、（x−1）（x−2）2-1 = （x+1）（x−3）3 ； 解：（x−1）（x−2）2 -1 = （x+1）（x−3）3 等式两边分子去括号x 2−3x+22 -1 = x 2−2x−33等式两边同时乘以63（x 2−3x +2）-6 =2（x 2−2x −3） 3x 2 -9x+6 -6= 2x 2 -4x −6x 2 -5x +6=0（x-2）（x-3）=0令x-2=0，解得x=2令x-3=0，解得x=3故原方程的根是：x 1=2，x 2=313、 14[12（x+1）+13（x+2）+2] =x 2；解：14[12（x+1）+13（x+2）+2] =x 2等号两边同时乘以412（x+1）+13（x+2）+2 =4x 2等号两边同时乘以63（x+1）+2（x+2）+12 =24x 23x+3+2x+4+12=24x 224x 2-5x-19=0（24x+19）（x-1）=0令24x+19=0，解得x= −1924令x-1=0，解得x= 1故原方程的根是：x 1=−1924，x 2= 114、（x+1）（x+2）+（x+3）（x+4）=（x+2）（x+3）+32；解：（x+1）（x+2）+（x+3）（x+4）=（x+2）（x+3）+32 等号两边去括号x 2+3x+2+x 2+7x+12 =x 2+5x+6+32整理得x 2+5x-24=0（x+8）（x-3）=0令x+8=0，解得x= -8令x-3=0，解得x= 3故原方程的根是：x 1=-8，x 2= 315、x=2（0.3x+21）3 - （0.2x−1）（x+2）2 ； 解：x= 2（0.3x+21）3 - （0.2x−1）（x+2）2等号两边同时乘以66x=4（0.3x+21）-3（0.2x-1）（x+2） 去括号6x=1.2x+84-0.6x 2+1.8x+6整理得0.6x 2+3x-90=0等号两边同时乘以10，然后再除以6 x 2+5x-150=0（x+15）（x-10）=0令x+15=0，解得x= -15令x-10=0，解得x= 10故原方程的根是：x 1= -15，x 2= 1016、x 2+（1+ 2√5）x +（ 4+√5）=0； 解：x 2+（1+ 2√5）x +（ 4+√5）=0 判别式△=（1+ 2√5）2-4・1・（ 4+√5）=1+4√5+20-16-4√5=5x= −（1+ 2√5）±√52∙1即x= −（1+ 2√5）+√52=−（1+ √5）2或 x= −（1+ 2√5）−√52=−（1+3 √5）2故原方程的根是：x1=−（1+ √5）2，x2= −（1+3 √5）2。

人教版七年级数学必刷题一、有理数运算类（5题）1. 计算：(-2)+3-(-5)- 解析：- 首先去括号，根据去括号法则，−(−5)=5。

- 则原式变为-2 + 3+5。

- 按照从左到右的顺序计算，-2+3 = 1，1 + 5=6。

2. 计算：-3×(-4)+(-28)÷7- 解析：- 先算乘除运算。

- 根据乘法法则，-3×(-4)=12，根据除法法则，(-28)÷7=-4。

- 再算加法，12+( - 4)=12 - 4 = 8。

3. 计算：(-2)^3+(-3)×[(-4)^2 - 2]- 解析：- 先计算指数运算。

(-2)^3=-8，(-4)^2 = 16。

- 然后计算括号内的式子，(-4)^2-2=16 - 2=14。

- 接着计算乘法，(-3)×14=-42。

- 最后计算加法，-8+( - 42)=-8 - 42=-50。

4. 计算：(1)/(2)×(-2)^2-((2)/(3))^2÷(2)/(9)- 解析：- 先算指数运算，(-2)^2 = 4，((2)/(3))^2=(4)/(9)。

- 然后计算乘除运算，(1)/(2)×4 = 2，(4)/(9)÷(2)/(9)=(4)/(9)×(9)/(2)=2。

- 最后计算减法，2 - 2=0。

5. 计算：(-1)^2023+ - 3(1)/(2)×(-6)- 解析：- 先计算指数运算，因为2023是奇数，所以(-1)^2023=-1。

- 再计算绝对值，- 3 = 3。

- 然后计算乘法，(1)/(2)×(-6)=-3。

- 最后计算加减运算，-1+3-( - 3)=-1 + 3+3=5。

二、整式加减类（5题）6. 化简：3a + 2b - 5a - b- 解析：- 合并同类项，3a-5a=(3 - 5)a=-2a，2b - b=(2 - 1)b=b。

经典初中数学试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项是二次方程的解？A. \(x = 2\)B. \(x = -3\)C. \(x = 4\)D. \(x = \frac{1}{2}\)答案：D2. 一个圆的半径是5厘米，那么这个圆的周长是多少？A. 10π厘米B. 20π厘米C. 30π厘米D. 40π厘米答案：B3. 如果一个数的相反数是-7，那么这个数是多少？A. 7B. -7C. 0D. 14答案：A4. 一个等腰三角形的底边长为6厘米，两腰长为5厘米，那么这个三角形的周长是多少？A. 16厘米B. 21厘米C. 26厘米D. 31厘米答案：B5. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 0答案：C二、填空题（每题2分，共10分）1. 一个数的平方是36，这个数是________。

答案：±62. 如果一个三角形的内角和为180°，其中一个角是90°，另外两个角的度数之和是________。

答案：90°3. 一个数除以3余2，除以5余3，除以7余2，这个数最小是________。

答案：534. 一个长方体的长、宽、高分别是10厘米、8厘米、5厘米，那么这个长方体的体积是________立方厘米。

答案：4005. 一个分数的分子是15，分母是30，这个分数化简后是________。

答案：\(\frac{1}{2}\)三、解答题（每题15分，共30分）1. 已知一个二次方程 \(ax^2 + bx + c = 0\) 的两个解是 \(x_1 =2\) 和 \(x_2 = -3\)，求出 \(a\)、\(b\)、\(c\) 的值。

答案：根据韦达定理，我们有 \(x_1 + x_2 = -\frac{b}{a}\) 和\(x_1 \cdot x_2 = \frac{c}{a}\)。

将 \(x_1 = 2\) 和 \(x_2 = -3\) 代入，得到 \(-1 = -\frac{b}{a}\) 和 \(-6 = \frac{c}{a}\)。

初中数学52个经典母题初中数学是学生们学习数学的重要阶段，掌握好基本概念和解题方法对于提高数学水平至关重要。

以下是初中数学中的52个经典母题，涵盖了各个知识点和解题方法，可以帮助学生系统地掌握数学知识。

1. 有一列数，第一个数是1，后面每个数都比前一个数多2，求第10个数是多少？2. 已知一个数是另一个数的1/4，这两个数的和是45，求这两个数分别是多少？3. 如果一个矩形的长是2/3，宽是6，求它的面积。

4. 若a+b=4，a-b=2，求a和b的值。

5. 一辆汽车每小时行驶60公里，行驶8个小时，求行驶的总里程数。

6. 已知一个数是另一个数的1/3，这两个数的差是24，求这两个数分别是多少？7. 如果一个圆的半径是5，求它的周长和面积。

8. 在一个平行四边形中，已知一条边长是6，另一条边长是8，求它的面积。

9. 有一列数，第一个数是3，后面每个数都比前一个数少4，求第10个数是多少？10. 若a-b=5，a+b=9，求a和b的值。

11. 一辆汽车每小时行驶80公里，行驶5个小时，求行驶的总里程数。

12. 一个长方形的长是4，宽是1/2，求它的面积。

13. 在一个正方形中，已知一条边长是3，求它的周长和面积。

14. 有一列数，第一个数是10，后面每个数都比前一个数多3，求第10个数是多少？15. 若a+b=7，a-b=1，求a和b的值。

16. 一辆汽车每小时行驶50公里，行驶10个小时，求行驶的总里程数。

17. 如果一个矩形的长是3/4，宽是8，求它的面积。

18. 已知一个数是另一个数的1/5，这两个数的差是30，求这两个数分别是多少？19. 如果一个圆的半径是8，求它的周长和面积。

20. 在一个平行四边形中，已知一条边长是5，另一条边长是7，求它的面积。

21. 有一列数，第一个数是20，后面每个数都比前一个数少2，求第10个数是多少？22. 若a-b=8，a+b=12，求a和b的值。

23. 一辆汽车每小时行驶70公里，行驶6个小时，求行驶的总里程数。

七年级数学经典例题一、有理数运算。

1. 计算：(-2)+3-(-5)- 解析：- 根据有理数的运算法则，减去一个数等于加上这个数的相反数。

- 所以(-2)+3 - (-5)=(-2)+3+5。

- 先计算(-2)+3 = 1，再计算1 + 5=6。

2. 计算：-2^2-( - 3)^3÷(-1)^2023- 解析：- 先计算指数运算。

-2^2=-4（这里注意指数运算的优先级，先计算指数2^2 = 4，再加上负号）。

- (-3)^3=-27，(-1)^2023=-1。

- 则原式=-4-(-27)÷(-1)。

- 接着计算除法-27÷(-1) = 27。

- 最后计算-4 - 27=-31。

二、整式的加减。

3. 化简：3a + 2b - 5a - b- 解析：- 合并同类项，同类项是指所含字母相同，并且相同字母的指数也相同的项。

- 对于a的同类项3a和-5a，合并得3a-5a=-2a。

- 对于b的同类项2b和-b，合并得2b - b=b。

- 所以化简结果为-2a + b。

4. 先化简，再求值：(2x^2 - 3xy + 4y^2)-3(x^2 - xy+(5)/(3)y^2)，其中x = - 2,y = 1- 解析：- 先去括号，根据去括号法则，括号前是正号，去掉括号不变号；括号前是负号，去掉括号要变号。

- 原式=2x^2-3xy + 4y^2-3x^2 + 3xy-5y^2。

- 再合并同类项，2x^2-3x^2=-x^2，4y^2-5y^2=-y^2，-3xy+3xy = 0。

- 化简结果为-x^2-y^2。

- 当x=-2,y = 1时，代入得-(-2)^2-1^2=-4 - 1=-5。

三、一元一次方程。

5. 解方程：3x+5=2x - 1- 解析：- 移项，把含有x的项移到等号一边，常数项移到等号另一边，移项要变号。

- 得到3x - 2x=-1 - 5。

- 合并同类项得x=-6。