下载文档原格式
证明一个映射是线性映射。
（P24,例1.4.9）
给定入口基及出口基，写出线性映射对应的矩阵表示。
求线性映射在不同基上的矩阵表示。
求最简形。
先通过初等行列变换化为阶梯形。
同时记录行变换（相当于左乘），列变换（右乘）。
即对In做变换。
记住Q是m*m，P是n*n，同时化为最简形时得到的是Q逆，还需要再进行变化得到Q。
所得结果也是该最简形在不同线性空间的基。
λ矩阵的行列式因子，不变因子和初等因子。
单位模阵。
求λ矩阵的Smith标准型。
两个矩阵相似的定义。
矩阵相似的三个条件。
求复数域上的矩阵的Jordan标准型。
内积-欧几里德空间
证明*是内积空间（欧几里得空间）
证明一个向量组是正交向量组。
施密特正交化化标准正交组。
复矩阵的奇异值和奇异值分解
复矩阵的奇异值分解
总结下：
A = UDV H ；AA H求U，A H A求V，注意维数问题，D和A同维度。
此外不够记住还有特征值为0的特征向量。
V=A H UD-H
（对于复数问题，记得转置；求λI n-AA H时,注意符号，对角线不为0的变负）
点到平面的距离：
A是平面（α1α2）投影矩阵得P，P=A（A T A）-1A T b，b表示一个向量，接着b-P即为距离，再套用距离公式计算长度。
正规矩阵酉相似对角化。
2 直接列写(1) 不含多端元件时的列写规则∑∑-===),()(节点之间支路导纳节点相连的支路导纳与j i y y i y ji ij ii (2) 含多端元件时的列写规则(a) 列出不含多端元件时的不定导纳矩阵，记作 'i Y (b) 将所有多端元件用VCCS 来等效，或将方程表达成电流是电压的函数(c) 考虑多端元件对原始不定导纳矩阵的影响： (a)、(b)对应行列元素相加i Y多端元件为电压控制电流源ab au b+-ab c gu d()()c a bd a b i g u u i g u u =-=--a b c g g d gg -⎡⎤⎢⎥-⎣⎦ijkl-+kl u ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-++-=ijjl ijjk ijil ijik i g y g y g y g y Y kli j klij u g多端元件为耦合电感元件**()ab a U s b +-()a I s ()c I s ()cd cU s d+-1L 2L M12()()()()ab a cd c U s I s sL sM U s I s sMsL ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦端口VCR 方程将其表达成电流是电压的函数22112()()1()()()a ab c cd I s U s L M I s U s ML s L L M -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦22112()()1()()()a ab c cd I s U s L M I s U s ML s L L M -⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦由此得互感元件对不定导纳矩阵的a 、b 、c 、d行及a 、b 、c 、d 列元的贡献，表示为以下4端电流用4端电压表达的方程22222111211()()()()1()()()()()a a b b c c d d I s U s L L M M I s U s LL M M U s M M L L I s s L L M U s M ML L I s --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦。
矩阵分析课程教学大纲一、课程基本信息课程编号：201411237课程中文名称：矩阵分析课程英文名称：Matrix Analysis课程性质：专业选修课程开课专业：应用数学开课学期：6总学时：36 （其中理论36学时）总学分：1.5二、课程目标本课程的学习内容是掌握域上线性空间的基本理论、矩阵分解方法及理论、矩阵的各种分析性质、各种广义逆矩阵及其与线性方程组的关系和广义逆矩阵的计算。
了解一些矩阵理论前沿的研究内容。
通过矩阵分析课程的学习，使学生掌握矩阵理论的基础知识和矩阵理论较前沿的成果，进而让学生受到严格的科学思维训练，掌握数学科学的思想方法，同时也为学生的后续学习做一定的知识上的储备，通过对一些知识点的课堂研讨，使学生加深知识的认知。
三、教学基本要求（含素质教育与创新能力培养的要求）矩阵分析这门课程对于数学系本科生来讲是一门非常重要的数学基础课，这就要求学生掌握如下矩阵基础理论知识：域上线性空间的基本理论；矩阵分解；矩阵广义逆；矩阵积分与微分。
了解一些矩阵理论前沿的研究，具备一定的创新能力。
具体要求如下：（1）具有应用已学习的知识点解决相应习题的能力；（2）能够解决较复杂、较抽象的问题；（3）具备将复杂问题简单化、抽象概念具体化，艰涩内容直白化, 逻辑推理自然化的素质;（4）具备读阅相关科研文献，撰写科研论文的能力，四、教学内容与学时分配1 绪论（6学时）1.1 线性空间基本理论1.2 线性变换及线性变换的矩阵表示2 矩阵分解（8学时）2.1 -矩阵及标准形2.2 初等因子与相似条件2.3 矩阵Jordan标准形 (研究型、研讨式教学模式)主要探讨矩阵若当标准形的得来，与初等因子、不变因子、行列式因子的关系2.4 矩阵的奇异值分解（研究型、研讨式教学模式）主要研讨矩阵奇异值定义的由来，基于变分法给出奇异值定义的表达式，研讨式给出矩阵奇异值分解。
2.5 单纯矩阵与正规矩阵的谱分解2.6 矩阵的满秩分解3 特殊矩阵（6学时）3.1 幂等矩阵3.2 幂零矩阵3.3 Hermite矩阵与Hermite二次型3.4 非负矩阵4 矩阵广义逆（6学时）4.1 矩阵{1}-逆及在线性方程组中的应用4.2 Moore-Penrose 逆及在线性方程组中的应用4.3 矩阵的谱广义逆（研究型、研讨式教学模式）主要研究矩阵分解在计算矩阵谱广义逆时的应用5 矩阵分析（8学时）5.1 矩阵范数5.2 矩阵级数5.3 矩阵的Kronecker积5.4 矩阵函数的微分（研究型、研讨式教学模式）主要以学生研讨式，给出三种矩阵微分公式及性质5.5 矩阵函数的积分6 科研论文讨论（2学时）（研究型、研讨式教学模式）通过读阅文献，研讨可研究的科研内容五、教学方法及手段（含现代化教学手段及研究性教学方法）多媒体授课与传统讲课方式相结合。
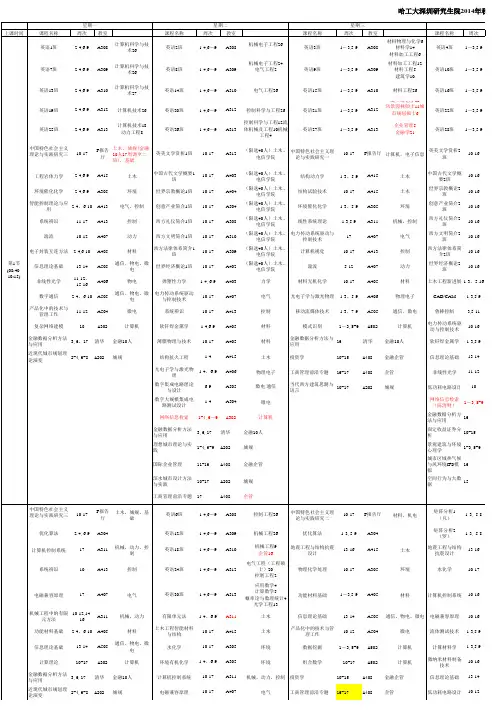
(10:30-星哈工大深圳研究生院2014年秋季专题设计2-4,6-14A202城规投资学15-16A408金融企管城市区域热气候与风环境CFD模拟16A202城规金融数据分析方法与应用16金融衍生工具9-14A408金融企管计量经济学7-12A408金融企管空间行为与大数据15A202城规创业学3，5-11工商管理前沿专题16-17A408企管空间行为与大数据15A202城规工商管理前沿专题16-17A408企管物流与供应链管理12-13空间行为与大数据15A202城规工商管理前沿专题17A408企管移动流媒体技术10-11A505通信、微电城市区域热气候与风环境CFD模拟16A202城规城市区域热气候与风环境CFD模拟16A202城规结构损伤识别10-15A415土木计算流体动力学1-4、6-9A415土木文艺与审美鉴赏5-8A104历史文明与国际关系10-13现代控制系统分析与设计2-4,6-10A311控制，电气工程岩体力学10A415土木结构损伤识别10-15A415土木自然辩证法概论一1-3,5生物医学信号2A505通信、微电、物电移动机器人导航理论1-4,6-8A413控制工程岩体力学1-3、5-9A415土木自然辩证法概论二6-9现代通信系统技术及方法论6-17A505通信、微电、物电生物医学信号1-2A505通信、微电、物电机械工程中的有限元方法9,17A311机械，动力环境生物技术9-16Verilog语言与及FPGA电路设计3-4A505微电、通信现代通信系统技术及方法论6-8A505通信、微电、物电移动机器人导航理论1-3,5-8A413控制有限单元法1-3、5-9算法设计与分析10-17A502计算机自然语言处理1-4, 6-9A502计算机最优控制10-17A413控制土木工程新进展10数据库系统原理2-4, 6-9A302计算机网络安全10-17A302计算机生物医学信号1-2A505通信、微电、物电并行处理与体系结构1-3、5-9现代通信系统技术及方法论9-17A505通信、微电、物电多维信号处理6-9自然语言处理1-3, 5-9A502计算机网络安全10-17算法设计与分析10-17A502计算机生物医学信号2A505通信、微电、物电生物医学信号1-2A505通信、微电、物电文艺与审美鉴赏5-8A104历史文明与国际关系10-13并行处理与体系结构2-4、6-10A504微电多维信号处理6-13A505通信生物医学信号1-2A505通信、微电、物电自然辩证法概论一1-3,5多维信号处理10-13A505通信自然辩证法概论二6-9生物医学信号1-2第5节(18:30-20:05)第6节(20:20-21:55)A504微电移动流媒体技术1-3.7-11A505通信、物电、微电A502计算机数据挖掘1－3,5-9A502计算机清华金融10人计算理论10-11、13-17A302计算机A408金融企管高级运筹学1-3,5-9A408金融企管A202城规结构抗火工程1－4A415土木A202城规A202城规A304控制76、电气48、机械机电动力89创业工程学10-13A104数值分析3（外聘）3、5-7、9-12A104电信学院109、计算机学院124力学11物理与工程中的数学方法3A304A104土木市政环境127、材料学院69应用随机过程1-3, 5-9A304自然辩证法概论三16F报告厅土木，城规，基础A312力学专业课结构可靠度理论与应用6-9A415土木生态城市设计理论与方法7-11,13-14,17A202城规F报告厅土木，城管除金10，基础高等土力学10-17A415土木组织行为学1-3,5-9A302管理A308专题课，其他学科若冲突可不选A311机械，动力污染场地风险分析与修复技术14-17A305环境A311机械，动力，控制最优控制10-17A413控制A415土木先进陶瓷材料10-17A405材料A505通信、微电子、物电、电气信息光子学1-3、5-6A504物电A505通信、物电、微电非线性光学7-9A406物电A302计算机数字大规模集成电路测试设计9A504微电清华金融10人设计模式1-3, 5-9A402计算机A408金融企管组合数学10-17A502计算机E206金融企管物流与供应链管理14-17E206企管行为科学研究方法1-3,5-9A408管理货币金融学16-17A408金融城市发展中的应用经济学1-3,5-9A202城规建设项目设计过程与评价10-13A202城规A104土木市政环境127、材料学院69创业工程学10-13A104数学之美15A104数学之美15A104F报告厅土木，城规，基础微分方程数值解1-3, 5-9A304物理与工程中的数学方法3A304A308专题课，其他学科若冲突可不选结构动力学1-3、5-9A415土木自然辩证法概论三16F报告厅土木，城管，基础科学技术史12A104A305环境结构试验技术10-17A415土木生态城市设计理论与方法7-11,13-14,17A202城规A311控制，电气运动控制1-3,5-9A311控制，电气组织行为学1-3,5-9A302管理A311机械，动力工程实验设计与分析10-17A311机械，动力数值分析3（外聘）3、5-7、9-12A104电信学院109、计算机学院124力学11A413控制计算机视觉10-17A413控制A502计算机材料物理10-17A405材料A505通信、物电A504微电子应用密码学10-17A402计算机A505微电通信物流与供应链管理14-17E206企管A302计算机行为科学研究方法1-3,5-9A408管理计算机货币金融学16-17A408金融清华金融10人城市发展中的应用经济学1-3,5-9A202城规A408金融企管建设项目设计过程与评价10-13A202城规E206金融企管A104科学技术史12A104科学技术史12A104科学技术史12A104 F报告厅计算机，电子信息金10计算流体动力学1-3、5-9A415土木数学之美15A104数学之美15A104F报告厅材料，机电移动机器人导航理论3,5A413控制A305环境生物医学信号1-2A505通信、微电、物电A311土木中国税收学2-3,5-11,13-14A202金融学A415土木数据库系统原理1-3, 5-10A302计算机A504微电A505通信A302计算机A104中国税收学2-3,5-11,13-14A202金融学F报告厅计算机，电子信息，金融10人生物医学信号1-2A505通信、微电、物电F报告厅材料，机电A505通信、微电、物电。
毕业论文开题报告数学与应用数学矩阵分解的研究一、选题的背景、意义数学作为一种创造性活动不仅拥有真理，而且拥有至高无上的美.矩阵是数学中的重要组成部分,因此对矩阵的研究具有重大的意义。
在近代数学、工程技术、经济理论管理科学中，大量涉及到矩阵理论的知识。
因此，矩阵理论自然就是学习和研究上述学科必不可少的基础之一。
矩阵理论发展到今天，已经形成了一整套的理论和方法，内容非常丰富。
矩阵分解对矩阵理论及近代计算数学的发展起了关键的作用。
寻求矩阵在各种意义下的分解形式，是对与矩阵有关的数值计算和理论都有着极为重要的意义。
因为这些分解式的特殊形式，一是能明显的反映出原矩阵的某些特征；二是分解的方法与过程提供了某些有效的数值计算方法和理论分析根据。
这些分解在数值代数和最优化问题的解决中都有着十分重要的角色以及在其他领域方面也起着必不可少的作用。
二、研究的基本内容与拟解决的主要问题本文简单的介绍了矩阵的定义，通过矩阵的定义，由m n ⨯个数(1,2,,,1,2,,)ij a K i m j n ∈==K K 排成的m 行、n 列的长方形表111212122212n n m m mn a a a a a a a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭K K M M O M K (1) 称为数域K 上的一个m n ⨯矩阵。
其中的ij a 称为这个矩阵的元。
两个矩阵相等就是它们对应位置的元全相等[1]。
矩阵通常用一个大写拉丁字母表示。
如（1）的矩阵可以被记为A .如果矩阵的行数m 与列数n 相等，则称它为n 阶方阵。
数域K 上所有m n ⨯矩阵的集合记为(),m n M K ,所有n 阶方阵的集合记为()n M K ，元全为0的矩阵称为零矩阵，记为0.矩阵A 的位于第i 行、第j 列的元简称为A 的(),i j 元，记为(),A i j 。
如果矩阵A 的(),i j 元是(1,2,,,1,2,,)ij a i m j n ==K K ，则可以写成()ij A a =。
博弈论——策略互动的艺术_哈尔滨工业大学中国大学mooc课后章节答案期末考试题库2023年1.观察如下的一个博弈树，【图片】下面结论正确的是（）。
答案:该博弈实质上是一个二人同时进行的博弈，其中参与人1的策略集为{a,b}，参与人2的策略集为{c, d}2.关于纳什均衡、子博弈完美均衡、完美贝叶斯均衡三个概念，下面说法正确的是（）。
答案:完美贝叶斯均衡一定是子博弈完美均衡3.关于博弈论纳什均衡的论述，下列说法中，（）是正确的。
答案:纳什均衡中任意一个参与人的对应策略，一定是关于该均衡中其他参与人在均衡中的策略或策略组合的最佳应对（best reply）4.下面例子，（）不属于博弈行为。
答案:樵夫在森林砍柴，樵夫和树木的关系5.再考虑孩子教育博弈问题，假设博弈支付矩阵如下所示孩子认真学习沉迷游戏母亲溺爱e, 21, f冷酷的爱a, bc, d如果在博弈均衡情况下，孩子的均衡策略是“认真学习”和“沉迷游戏”策略的完全非退化随机化（孩子均以严格正概率选择这两个策略），且博弈只存在一个纳什均衡，那么下面表述为真的选项是( )答案:母亲也必须对“溺爱”和“冷酷的爱”进行完全非退化的随机化（以严格正概率选择“溺爱”和“冷酷的爱”）6.考虑如下的孩子教育博弈，支付矩阵如下（a，b，c均大于0）孩子认真学习沉迷游戏母亲溺爱3, 21, 3冷酷的爱a, bc, d如果希望博弈均衡为（冷酷的爱，认真学习），那么a～d需要满足的条件为（）答案:a≥3且b≥d7.对于如下图所示的博弈【图片】若参与人1选择行动L、M和R的概率分别为0.2，0.3和0.5，那么根据“策略-信念”的一致性要求，当博弈到达参与人2的信息集时，下面选项正确的是（）。
答案:参与人2认为她在左边决策节点的概率和右边节点的概率分别为0.4和0.6 8.目前新能源汽车在世界范围内处于方兴未艾的状态，关于新能源汽车行业，从博弈“竞合”角度，下面说法合理的是（）（可多选）答案:提升电动汽车电池续航能力会增加汽车的价值_适度的国内竞争，会有利于我国新能源汽车行业的发展_在相对偏僻的商场增设充电桩，会实现商场和新能源汽车销售企业的共赢9.关于博弈“竞合”的表述，最为贴切的表述是（）答案:竞合的含义是，竞争与合作同时存在的过程10.下面选项哪个不属于破解囚徒困境的方法（）答案:事先制定君子协定11.改变博弈的PARTS法中，S的含义是（）答案:Scope 博弈的范围12.下面关于博弈树的说法，正确的是（）。
