卢瑟福公式
- 格式:doc
- 大小:176.00 KB
- 文档页数:4

卢瑟福散射卢瑟福散射实验是近代物理学发展史上具有重大影响的实验,它的作用在于由此发现并提出了原子的核式模型,使人类对微观世界的认识进入了新的里程。
后来,人们进而创造了一种用粒子的散射来研究物质结构的新实验方法——卢瑟福散射。
现在该方法成为材料科学,特别是微电子应用领域的重要实验方法之一。
19世纪末20世纪初,原子结构开始成为物理学研究的前沿,人们对原子模型曾有各种猜测和设想,其中比较有影响的是美国物理学家汤姆孙(J. J. Thomson )的电子分布模型,该模型认为正电荷均匀地分布在整个原子球内,一定数目的电子“镶嵌”在这个球体或球面上,电子可以在它们的平衡位置附近振动,从而发出特定频率的电磁波。
这个模型似乎可以解释当时已观察到的原子光谱,但很多其它实验不能解释,事实很快否定了这一模型。
1909年,卢瑟福(Lord Ernest Rutherford )和其合作者盖革(H. Gelger )与马斯顿(E. Marsden )用天然放射性Ra 所发出的α粒子打到Pt 箔上,发现绝大部分α粒子平均只偏转2º~3º,但大约有1/8000的α粒子散射角大于90º,甚至接近180º,即发现存在大角度散射的物理现象。
用当时的汤姆孙模型无法解释大角度的散射,卢瑟福认为原子中的正电荷应该是紧密地集中在一起的,当α粒子碰到这点时就被弹了回来。
由于具有对物理现象深刻的洞察力,卢瑟福最终提出了原子的核式模型。
在该模型中,原子核的半径近似为10-13 cm ,约为原子半径的1/105。
卢瑟福散射实验给了我们正确的有关原子结构的图像,开创了人类认识物质世界的新起点。
而卢瑟福本人因对物理学的重大贡献获得诺贝尔物理学奖。
一 实验目的测量241Am (或239Pu )放射源的α粒子在金箔上不同角度散射的分布,并与理论结果比较,从而验证卢瑟福散射的理论。
二 实验原理卢瑟福散射的基本思想:α粒子被看作一带电质点,在核库仑场中的运动遵从经典运动方程;原子核的大小和原子相比是很小的,且原子核具有正电荷Ze 和原子的大部分质量;电子的质量很小,对α粒子运动的影响可忽略不计。


陈杨PB05210097 物理二班实验题目:卢瑟福散射实验实验目的:1.通过卢瑟福核式模型,说明α粒子散射实验,验证卢瑟福散射理论;2.并学习应用散射实验研究物质结构的方法。
实验原理:现从卢瑟福核式模型出发,先求α粒子散射中的偏转角公式,再求α粒子散射公式。
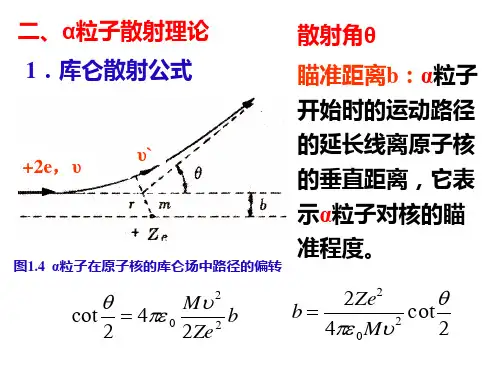
1.α粒子散射理论(1)库仑散射偏转角公式设原子核的质量为M,具有正电荷+Ze,并处于点O,而质量为m,能量为E,电荷为2e的α粒子以速度ν入射,在原子核的质量比α粒子的质量大得多的情况下,可以认为前者不会被推动,α粒子则受库仑力的作用而改变了运动的方向,偏转θ角,如图所示。
图中ν是α粒子原来的速度,b是原子核离α粒子原运动径的延长线的垂直距离,即入射粒子与原子核无作用时的最小直线距离,称为瞄准距离。
图α粒子在原子核的库仑场中路径的偏转当α粒子进入原子核库仑场时,一部分动能将改变为库仑势能。
设α粒子最初的的动能和角动量分别为E和L,由能量和动量守恒定律可知:⎪⎪⎭⎫⎝⎛++⋅=••222202241ϕπεr r m r Ze E (1)L b m mr ==••νϕ2 (2)由(1)式和(2)式可以证明α粒子的路线是双曲线,偏转角θ与瞄准距离b 有如下关系:202242Ze Ebctgπεθ= (3)设E Ze a 0242πε=,则 a bctg22=θ(4)这就是库仑散射偏转角公式。
(2)卢瑟福散射公式在上述库仑散射偏转公式中有一个实验中无法测量的参数b ,因此必须设法寻找一个可测量的量代替参数b 的测量。
事实上,某个α粒子与原子散射的瞄准距离可大,可小,但是大量α粒子散射都具有一定的统计规律。
由散射公式(4)可见,θ与b 有对应关系,b 大,θ就小,如图所示。
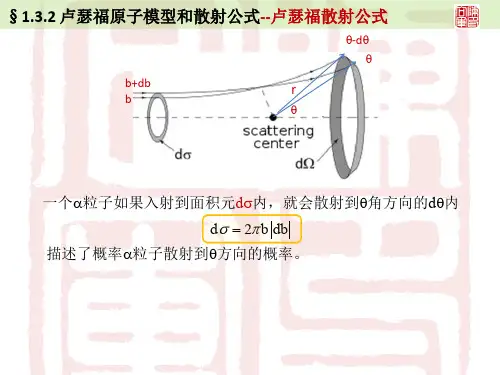
那些瞄准距离在b 到db b +之间的α粒子,经散射后必定向θ到θθd -之间的角度散出。
因此,凡通过图中所示以b 为内半径,以db b +为外半径的那个环形ds 的α粒子,必定散射到角θ到θθd -之间的一个空间圆锥体内。


3系08级 姓名:方一 日期:6月6日 PB08206045实验题目: 卢瑟福散射 实验目的: 通过卢瑟福核式模型,说明α粒子散射实验,验证卢瑟福散射理论;并学习应用散射实验研究物质结构的方法。
实验原理:现从卢瑟福核式模型出发,先求α粒子散射中的偏转角公式,再求α粒子散射公式。
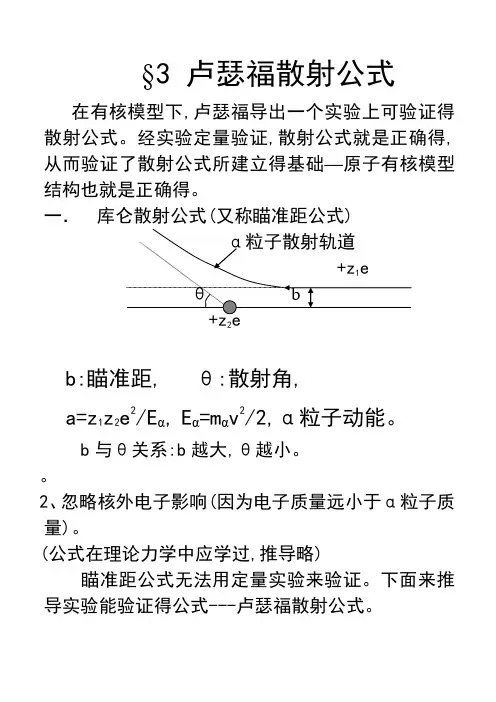
1.α粒子散射理论 (1)库仑散射偏转角公式设原子核的质量为M ,具有正电荷+Ze ,并处于点O ,而质量为m ,能量为E ,电荷为2e 的α粒子以速度ν入射,在原子核的质量比α粒子的质量大得多的情况下,可以认为前者不会被推动,α粒子则受库仑力的作用而改变了运动的方向,偏转θ角,如图3.3-1所示。
图中ν是α粒子原来的速度,b 是原子核离α粒子原运动径的延长线的垂直距离,即入射粒子与原子核无作用时的最小直线距离,称为瞄准距离。
图3.3-1 α粒子在原子核的库仑场中路径的偏转当α粒子进入原子核库仑场时,一部分动能将改变为库仑势能。
设α粒子最初的的动能和角动量分别为E 和L ,由能量和动量守恒定律可知:⎪⎪⎭⎫⎝⎛++⋅=∙∙222202241ϕπεr r m r Ze E (1) L b m mr ==∙∙νϕ2 (2)由(1)式和(2)式可以证明α粒子的路线是双曲线,偏转角θ与瞄准距离b 有如下关系:22242Ze Ebctgπεθ= (3) 设E Ze a 0242πε=,则a b ctg 22=θ (4)这就是库仑散射偏转角公式。
(2)卢瑟福散射公式在上述库仑散射偏转公式中有一个实验中无法测量的参数b ,因此必须设法寻找一个可测量的量代替参数b 的测量。
事实上,某个α粒子与原子散射的瞄准距离可大,可小,但是大量α粒子散射都具有一定的统计规律。
由散射公式(4)可见,θ与b 有对应关系,b 大,θ就小,如图3.3-2所示。
那些瞄准距离在b 到db b +之间的α粒子,经散射后必定向θ到θθd -之间的角度散出。
因此,凡通过图中所示以b 为内半径,以db b +为外半径的那个环形ds 的α粒子,必定散射到角θ到θθd -之间的一个空间圆锥体内。
§3 卢瑟福散射公式在有核模型下,卢瑟福导出一个实验上可验证得散射公式。
经实验定量验证,散射公式就是正确得,从而验证了散射公式所建立得基础—原子有核模型结构也就是正确得。
一.库仑散射公式(又称瞄准距公式)2b:瞄准距, θ:散射角,a=z1z2e2/Eα,Eα=mαv2/2,α粒子动能。
b与θ关系:b越大,θ越小。
2、忽略核外电子影响(因为电子质量远小于α粒子质量)。
(公式在理论力学中应学过,推导略)瞄准距公式无法用定量实验来验证。
下面来推导实验能验证得公式---卢瑟福散射公式。
二.卢瑟福得散射公式1.装置图M:显微镜2.卢瑟福得散射公式说明:dN´: 散射到散射角为θ、立体角为dΩ得α粒子数dΩ:闪烁屏S对散射点O展开得立体角;E:α粒子动能,E=mv2/2;Z1=2, Z2=79(金得电荷数)t: 金箔厚度;n: 箔中单位体积中原子数(原子数密度);N:入射得α粒子总数3.卢瑟福得散射公式推导,并介绍一个重要概念:微分散射截面。
θ①左边得对应得空心园锥体内散射出来。
(两个园锥体得顶点可近似重合),一个右边小园环总就是与左边一个空心园锥体对应。
现推导小园环dσ与空心园锥体得立体角dΩ得关系:这就就是dΩ与dσ得关系式。
并且由于对称性,此式对出射得任意立体角dΩ'与对应得入射小截面dσ'得关系也成立。
②求与一个原子核碰撞,从dΩ散射出来得α粒子数dN(假设α粒子穿过箔片时只发生一次散射)A入射α粒子散射α粒子厚度t设通过A得入射α粒子总数为N,则单位面积上通过α粒子数为N/A,那么通过某一小截面dσ得α粒子数为:这就是α粒子与一个原子核碰撞,散射到散射角为θ、立体角为dΩ得α粒子数dN。
③那么被A面积中所有原子核散射到散射到同一散射角为θ、立体角为dΩ得α粒子数dN'为:----卢瑟福散射公式(假设不同原子核对同一闪烁屏得立体角与散射角近似相等)④微分散射截面σcdσ就是一个很重要得物理量,于就是把单位立体角对应得小截面称为微分散射截面或有效散射截面,即:σc得物理意义;表示α粒子被箔片中一个靶核散射时,散射到散射角为θ得单位立体角中得几率。

卢瑟福散射与原子核半径卢瑟福散射是物理学中非常重要的实验现象之一,它是研究原子核结构的重要方法之一。
在这个实验中,来自天然放射性物质的α粒子轰击金属薄膜,进而散射到不同的角度。
通过分析散射后的α粒子的轨迹和散射的总体趋势,我们可以了解到原子核的存在和性质。
卢瑟福散射实验最早由英国物理学家欧内斯特•卢瑟福于20世纪初进行。
当时他使用的是金箔作为散射靶材,并发现了令人震惊的结果,即大部分α粒子经过金箔时几乎不受到阻碍,只有少部分粒子发生散射。
这个实验结果违背了当时的物理学理论,因为按照汤姆逊的原子模型来看,如果原子是一个均匀分布的正电荷球,那么散射的概率应该是均匀分布的,而卢瑟福实验观察到的散射角分布是高度不均匀的。
卢瑟福据此提出了一个新的原子模型,即著名的卢瑟福模型,也被称为太阳系模型。
根据这个模型,原子核是一个带正电荷的小球,而电子则绕着核运动。
这个模型将原子核的概念引入了物理学,并为理解散射现象提供了合理的解释。
根据卢瑟福模型,散射的概率与散射角度呈反比关系,即散射角度越大,散射的概率越小。
通过卢瑟福散射实验,我们不仅可以了解原子核的存在,还可以通过测量不同角度下的散射偏转角度来推算出原子核的大小。
根据卢瑟福的计算,可以得到一个简单的公式:R=K(θ/2)tan(θ/2) ,其中 R代表原子核半径,θ代表散射偏转角度,K是一个与散射实验条件有关的常数。
通过测量不同的散射角度,我们可以利用这个公式来估算原子核的大小。
卢瑟福散射实验的结果对物理学的发展产生了重大影响。
首先,它验证了原子是由带正电荷的原子核和绕核运动的电子组成的这一假设。
其次,它揭示了原子核的存在和性质,使得人们对原子结构有了更深入的认识。
此外,卢瑟福模型的提出也为后来的量子力学提供了重要的启示,为物理学的进一步发展打下了基础。
总之,卢瑟福散射实验的结果提供了理解原子核结构的重要线索,为后来的原子物理学研究奠定了基础。
通过测量散射偏转角度,我们可以推算出原子核的大小,这对于了解原子核的组成和性质具有重要意义。

卢瑟福散射公式的推导及谈α粒子散射实验的应用意义摘要1909年卢瑟福和他的助手盖革(H.Geiger)及学生马斯登(E.Marsden)在做α粒子和薄箔散射实验时观察到绝大部分α粒子几乎是直接穿过铂箔,但偶然有大约1/8000α粒子发生散射角大于90°。
这一实验结果当时在英国被公认的汤姆逊原子模型根本无法解释。
在汤姆逊模型中正电荷分布于整个原子,根据对库仑力的分析,α粒子离球心越近,所受库仑力越小,而在原子外,原子是中性的,α粒子和原子间几乎没有相互作用力。
在球面上库仑力最大,也不可能发生大角度散射。
卢瑟福等人经过两年的分析,于1911年提出原子的核式模型,原子中的正电荷集中在原子中心很小的区域内,而且原子的全部质量也集中在这个区域内。
原子核的半径近似为10,约为原子半径的千万分之一。
α粒子散射实验是物理学史上具有里程碑意义的重要实验之一,评为“最美丽”的十大物理实验之三。
由α散射实验现象确立了原子的核式结构,为现代物理的发展奠定了基石。
从20世纪60年代中后期首先应用卢瑟福背散射于月球表面元素成分分析至今,成为成为一种常规的杂质成分、含量及深度分布、膜厚度分析手段。
本文首先介绍原子的的大小和质量,然后介绍原子有核模型提出的历史过程和α粒子散射实验的过程,根据α粒子散射实验中不可忽视的大角度散射引出卢瑟福原子模型,运用相关数学手段和理论力学的基本知识具体详细的推导出库伦散射公式和卢瑟福散射公式,指出了行星模型的意义和困难,并阐述了α粒子散射实验实际应用意义和α粒子试验仪在天体物理中的应用,在最后对相关数学手段和理论力学的相关知识进行了详细的介绍。
关键词:α粒子散射实验;库仑散射公式;卢瑟福散射公式;行星模型;原子稳定性AbstractIn 1909,Rutherford and his assistant Geiger (H. Geiger) and students Marsden (E. Marsden) doing α particles and thin foil scattering experiments observed that most of the α-particles is almost directly through the platinum foil But occasionally, about 1/8000α particles in the scattering angle greater than 90 °. The results of this experiment was to be accepted in the United Kingdom Thomson atomic model could not explain. Chiang Kai-shek in the Thomson model of charge distribution in the atom, based on the analysis of Coulomb force, α par ticles from the hot core closer, suffered the smaller Coulomb force, and in the atom, the atom is neutral, α particles and atoms almost no interaction. Coulomb force in the largest sphere, large angle scattering can not occur. Rutherford, who after two years of analysis, in 1911 proposed the nuclear atom-type model, the positive charge concentration of atoms at the atomic center of a very small area, and the atoms of all the quality of focus within the region. Radius of the nucleus is approximately 10, approximately ten-millionth of atomic radius. α-particle scattering experiment is a milestone in the history of physics in one of the important experiments, as the "most beautiful" of the top ten physics experiments III. Established by the α scattering behavio r of atoms and nuclear structure, the development of modern physics have laid a foundation. 60 years from the late 20th century, first applied Rutherford backscattering elemental composition analysis on the lunar surface so far as to become a routine impurity content and depth distribution, film thickness analysis tool. This paper describes the size and quality of the atom, then introduces a nuclear atom model proposed by the historical process and α-particle scattering process, according to α-particle scattering experiment can not be ignored in the large angle scattering leads to Rutherford atomic model, the use of relevant mathematics tools and basic knowledge of theoretical mechanics specific detailed Coulomb scattering formula is derived and the Rutherford scattering formula, that the planetary model of the significance and difficulties, and described the practical application of α-particle scattering experiment significance and α particle tester in astrophysics application of mathematical methods in the final of the relevant knowledge and theoretical mechanics, a detailed description.Keywords:Alpha particle Scattering experiments; Coulomb scattering formula; Rutherford formula; planetary model; Atomic stability目录绪论-------------------------------------------------------- 1第一章背景知识-------------------------------------------- 31.1 电子的发现------------------------------------------------------- 3 1.2 电子的电荷和质量-------------------------------------------------- 4 1.3 阿伏伽德罗常数---------------------------------------------------- 4 1.4 原子的大小------------------------------------------------------- 4第二章原子核式结构理论提出的历史过程----------------------- 62.1 汤姆孙在发现电子后提出的原子结构设想------------------------------ 6 2.2 开尔文原子模型---------------------------------------------------- 6 2.3 汤姆孙的葡萄干—布丁原子模型-------------------------------------- 7 2.4 勒那德的原子模型-------------------------------------------------- 7 2.5 长岗的土星原子模型------------------------------------------------ 8 2.6 尼克尔森的初始物质原子结构--------------------------------------- 9第三章α粒子散射实验及大角度散射现象的思考--------------- 103.1 α粒子散射实验--------------------------------------------------- 10 3.2 大角度散射现象引出的思考和核式模型的由来------------------------- 11第四章库伦散射公式及卢瑟福散射公式的推导------------------ 144.1 库伦散射公式----------------------------------------------------- 14 4.2 卢瑟福散射公式--------------------------------------------------- 16第五章卢瑟福理论的实验验证------------------------------- 185.1 卢瑟福散射公式的拓展--------------------------------------------- 18 5.2 卢瑟福理论的实验验证--------------------------------------------- 19 5.3 关于小角与180°处的卢瑟福公式----------------------------------- 21第六章α粒子散射实验的应用意义--------------------------- 226.1 对于α粒子散射实验的回顾和一些说明------------------------------ 22 6.2 用α粒子散射实验估计原子核大小--------------------------------- 22 6.3 α粒子散射实验的新应用——卢瑟福背散射分析---------------------- 24 6.4 粒子散射实验给我们今天留下的财富 ----------------------------- 24第七章行星模型的意义和困难-------------------------------- 267.1 行星模型的意义--------------------------------------------------- 26 7.2 行星模型的困难--------------------------------------------------- 26参考文献--------------------------------------------------- 28附录------------------------------------------------------- 29附录A 中心力---------------------------------------------------- 29附录B 极坐标------------------------------------------------------ 30附录C 两体问题--------------------------------------------------- 33绪论原子物理学是研究原子结构,运动规律及相互作用的物理学的一个分支,主要研究:原子的电子结构、原子光谱、原子之间或与其他物质的碰撞过程和相互作用。
§2、§3、§4三节介绍卢瑟福有核模型。
历史上先出现的是汤姆逊的原子实心模型,然后经卢瑟福的α散射实验,修正为原子有核模型。
§2 卢瑟福有核模型的提出§3 卢瑟福散射公式§4 卢瑟福公式的实验验证§2 卢瑟福(有核)模型的提出一.汤姆逊的原子实心模型当时已有的关于原子的实验事实:1.原子内部有带负电荷的电子,原子中性;2.原子会发光,原子大小~ Å。
汤姆逊根据以上实验事实,提出了原子实心模型,称汤姆逊模型:1.正电部分是一个实心球体,大小~ Å,正电荷均匀分布;2.电子对称地嵌在实心球体上,并在平衡位置作微振动。
这个模型把当时已有的关于原子的实验事实都给予了解释,从而被人们所接受。
二.卢瑟福的α散射实验及结果1.实验装置(p27)M:显微镜;S:闪烁屏;F:金箔片2.实验结果:大多数散射的α粒子的散射角θ<3°,但有少数(占1/800)α粒子的散射角θ>90°,甚至接近180°。
关键是这个大散射角θ,把汤姆逊模型否定了。
卢瑟福的话‘这如同15英寸的炮弹打在一张纸上被弹回来一样是不可思议的‘。
为了能产生大散射角,卢瑟福提出了原子有核模型。
三.汤姆逊模型不可能产生大于90°大散射角,只有有核模型结构才有可能。
二点假设前提:1.原子核静止。
因为原子核质量(如金核的 A=196)远大于α粒子质量(A=4))。
如果要考虑到散射过程中α粒子与原子核都在运动,只要用折合质量μ=Mmα/(M+ mα)代替公式中的mα,所得公式就是二体都在运动的正确公式。
2.忽略核外电子影响(因为电子质量远小于α粒子质量)。
1.α粒子受二种模型作用力的比较:F Fo R r o RR r R»R’实心模型有核模型r<R, F=2Ze2r/R3r≥R, F=2Ze2/r2r>R’, F=2Ze2/r2F MAX=2Ze2/R22. 理论估计汤姆逊模型的最大散射角。
实验3.3 卢瑟福散射实验卢瑟福散射实验是近代物理科学发展史中最重要的实验之一。
在1897年汤姆逊(J.J.Thomson)测定电子的荷质比,提出了原子模型,他认为原子中的正电荷分布在整个原子空间,即在一个半径R≈10-10m区间,电子则嵌在布满正电荷的球内。
电子处在平衡位置上作简谐振动,从而发出特定频率的电磁波。
简单的估算可以给出辐射频率约在紫外和可见光区,因此能定性地解释原子的辐射特性。
但是很快卢瑟福(E.Rutherford)等人的实验否定这一模型。
1909年卢瑟福和他的助手盖革(H.Geiger)及学生马斯登(E.Marsden)在做α粒子和薄箔散射实验时观察到绝大部分α粒子几乎是直接穿过铂箔,但偶然有大约1/800α粒子发生散射角大于900。
这一实验结果当时在英国被公认的汤姆逊原子模型根本无法解释。
在汤姆逊模型中正电荷分布于整个原子,根据对库仑力的分析,α粒子离球心越近,所受库仑力越小,而在原子外,原子是中性的,α粒子和原子间几乎没有相互作用力。
在球面上库仑力最大,也不可能发生大角度散射。
卢瑟福等人经过两年的分析,于1911年提出原子的核式模型,原子中的正电荷集中在原子中心很小的区域内,而且原子的全部质量也集中在这个区域内。
原子核的半径近似为10-15m,约为原子半径的千万分之一。
卢瑟福散射实验确立了原子的核式结构,为现代物理的发展奠定了基石。
本实验通过卢瑟福核式模型,说明α粒子散射实验,验证卢瑟福散射理论;并学习应用散射实验研究物质结构的方法。
实验原理现从卢瑟福核式模型出发,先求α粒子散射中的偏转角公式,再求α粒子散射公式。
1.α粒子散射理论(1)库仑散射偏转角公式设原子核的质量为M,具有正电荷+Ze,并处于点O,而质量为m,能量为E,电荷为2e的α粒子以速度ν入射,在原子核的质量比α粒子的质量大得多的情况下,可以认为前者不会被推动,α粒子则受库仑力的作用而改变了运动的方向,偏转θ角,如图3.3-1所示。
卢瑟福散射公式表达式
1. 卢瑟福散射公式。
- 在卢瑟福散射实验的基础上,推导出卢瑟福散射公式。
设靶核的电荷为Ze (Z为原子序数,e为元电荷),入射粒子的电荷为ze,入射粒子的速度为v,瞄准距离(入射粒子与靶核无相互作用情况下的最小距离)为b。
- 卢瑟福散射公式为:
(dN)/(Ndt)=<=ft((1)/(4πε_0))^2<=ft(frac{Ze^2ze^2}{4E})^2(ntdΩ)/(sin^4)(θ/2)
- 其中各物理量的含义如下:
- (dN)/(Ndt):表示单位时间内散射到(θ,θ + dθ)立体角内的粒子数dN与入射粒子总数N之比。
- ε_0:真空介电常数。
- E=(1)/(2)mv^2为入射粒子的能量(m为入射粒子质量)。
- n:靶物质单位体积内的原子核数。
- t:靶的厚度。
- dΩ = 2πsinθ dθ:立体角元。
- θ:散射角。
卢瑟福散射
维基百科,自由的百科全书
(重定向自卢瑟福散射)
跳转到:导航、搜索
上方:预期结果:阿尔法粒子不受到扰动地通过梅子布丁模型。
下方:观测结果:一小部分阿尔法粒子被反弹,表明全部正电荷集中于一个很小的区域。
在原子物理学里,卢瑟福散射(英语:Rutherford scattering)是一个散射实验,由欧尼斯特·卢瑟福领队设计与研究,成功地于 1909 年证实在原子的中心有个原子核[1],也导至卢瑟福模型(行星模型)的创立,及后来玻尔模型的提出。
应用卢瑟福散射的技术与理论,卢瑟福背散射(Rutherford backscattering)是一种专门分析材料的技术。
卢瑟福散射有时也被称为库仑散射,因为它涉及的位势乃库仑位势。
深度非弹性散射(deep inelastic scattering)也是一种类似的散射,在 60 年代,常用来探测原子核的内部。
目录
[隐藏]
∙ 1 历史
∙ 2 微分截面
∙ 3 原子核最大尺寸
∙ 4 应用
∙ 5 参阅
∙ 6 参考文献
[编辑]历史
阿尔法粒子散射的实验完成于1909年。
在那时代,原子被认为类比于梅子布丁(物理学家约瑟夫·汤姆孙提出的),负电荷(梅子)分散于正电荷的圆球(布丁)。
假若这梅子布丁模型是正确的,由于正电荷完全散开,而不是集中于一个原子核,库仑位势的变化不会很大,通过这位势的阿尔法粒子,其移动方向应该只会有小角度偏差。
在卢瑟福的指导下,汉斯·盖革(Hans Geiger)和欧内斯特·马士登(Ernest Marsden)发射阿尔法粒子射束来轰击非常薄、只有几个原子厚度的金箔纸[2]。
然而,他们得到的实验结果非常诡异,大约每8000个阿尔法粒子,就有一个粒子的移动方向会有很大角度的偏差(甚至超过 90°);而其它粒子都直直地通过金箔纸,偏差几乎在2°到3°以内,甚至几乎没有偏差。
从这结果,卢瑟福断定,大多数的质量和正电荷,都集中于一个很小的区域(这个区域后来被称作“原子核”);电子则包围在区域的外面。
当一个(正价)阿尔法粒子移动到非常接近原子核,它会被很强烈的排斥,以大角度反弹。
原子核的小尺寸解释了为什么只有极少数的阿尔法粒子被这样排斥。
卢瑟福对这奇异的结果感到非常惊异。
正如同他后来常说的:“这就好像你朝一张卫生纸射出一枚15吋的炮弹,炮弹却弹回来打中你一样。
”[3]
卢瑟福计算出原子核的尺寸应该小于。
至于其具体的数值,卢瑟福无
法从这实验决定出来。
关于这一部份,请参阅后面的“原子核最大尺寸”一节。
[编辑]微分截面
一个粒子的排斥散射。
所有通过左边圆环的粒子,感受到位势的作用,必定
会通过右边圆环。
卢瑟福计算出来的微分截面是
;
其中,是截面,是立体角,是阿尔法粒子的电荷量,是散射体的电荷量,是真空电容率,是能量,是散射角度。
[编辑]原子核最大尺寸
假设阿尔法粒子正面碰撞于原子核。
阿尔法粒子所有的动量(),在碰撞点,都被转换为位能。
在那一刹那,阿尔法粒子暂时是停止的。
从阿尔法粒子
到原子核中心的距离是原子核最大尺寸。
应用库仑定律,
;
其中,是质量,是初始速度。
重新编排,。
阿尔法粒子的质量是,电荷量是
,初始速度是,金的电荷量
是。
将这些数值代入方程,可以得到撞击参数
(真实半径是)。
这些实验无法得到真
实半径,因为阿尔法粒子没有足够的能量撞入半径内。
卢瑟福知道这问
题。
他也知道,假若阿尔法粒子真能撞至半径,直接地击中金原子核,
那么,在高撞击角度(最小撞击参数),由于位势不再是库仑位势,实验得到的散射曲线的样子会从双曲线改变为别种曲线。
卢瑟福没有观察到别种曲线,显示出金原子核并没有被击中。
所以,卢瑟福只能确定金原子核的半径小于。
1919 年,在卢瑟福实验室进行的另一个非常类似的实验,物理学家发射阿尔法粒子于氢原子核,观察到散射曲线显著地偏离双曲线,意示位势不再是库仑位势。
从实验数据,物理学家得到撞击参数或最近离距(closest approach)大约为。
更进一步的研究,在卢瑟福实验室,发射阿尔法粒子于氮原子核和氧
原子核,得到的结果,使得詹姆斯·查德威克和工作同仁确信,原子核内的作用力不同于库仑斥力[4]。
[编辑]应用
现今,应用这些年累积的散射原理与技术,卢瑟福背散射谱学能够侦侧半导体内的重金属杂质。
实际上,这技术也是第一个在月球使用的实地分析技术。
在勘察者任务(surveyor mission)降落于月球表面后,卢瑟福背散射谱学实验被用来收集地质资料。
[编辑]参阅
∙汤姆孙散射
∙散射理论
[编辑]参考文献
1.^卢瑟福, 欧尼斯特. The Scattering of α and β Particles by Matter and
the Structure of the Atom, 21. May 1911: p. 669-688 [2008年12月21日].
2.^ Geiger, Hans; Marsden, Ernest, On a Diffuse Reflection of the α
-Particles, Proceedings of the Royal Society. 1909, 82 (A): p. 495-500
3.^萧如珀; 杨信男, 卢瑟福和原子核的发现, 物理双月刊. Jun, 2007, 29 (3)
4.^派斯, 亚伯拉罕. Inward Bound: Of Matter and Forces in the Physical
World. USA: Oxford University Press. September 29, 1988: pp. 239.
ISBN978-0198519973.
来自“/w/index.php?title=拉塞福散射
&oldid=19163163”
查看条目评分
给本文评分。