热机循环
- 格式:doc
- 大小:733.50 KB
- 文档页数:6



热机循环热力发动机(热机)是指各种利用内能做功的机械,其原理是将燃料的化学能转化成内能再转化成机械能的机器动力机械的一类,如蒸汽机、汽轮机、燃气轮机、内燃机、喷气发动机等。
热机通常以气体作为工质(传递能量的媒介物质叫工质),利用气体受热膨胀对外做功。
自热机出现以来,人们一直从实验和理论上研究其效率问题。
大量研究工作一方面为提高热机效率指明了的方向,另一方面推动了热学理论的发展。
【实验目的】(1)研究热机将热转换为功的过程和原理 (2)学会计算热机循环的效率 (3)探索提高热机循环效率的方法【实验原理】热机是依靠从热源吸收热量,向低温热源释放热量来工作一种的装置。
其理论基础为:(一) 理想气体方程式:PV=nRT ,将热力系统视为理想气体,再经热力过程变化时,将满足理想气体方程式。
(二)热力学第一定律:热力过程的变化,由能量守恒的推导,可得:dU = dQ - dW 。
dU 为系统内能变化,dQ 为加入系统的热能,dW 为系统对外界所做的功。
1. 内能函数U 为状态函数,故热力系统经一循环过程,末状态等于初状态,其内能相同,故dU = 0。
2. dQ 为热力过程加入系统的热能,其值和变化的过程有关:绝热过程:dQ = 0。
等压过程:dQ = nC p dT 。
定容过程:dQ = nC v dT 。
其中C p 、C v 分别为气体的定压比热及定容比热。
若系统吸热,dQ 为正值;若排热,dQ 为负值。
3. dW 为热力系统在热力过程中对外界所做的功,其形式为:dW = PdV ,dW 为微量变化的功,在这一完整过程种做功为⎰⎰==PdVdW W ,即热力系统P-V 图曲线下面积。
故: 等压过程:W = P∆V = P(12V V -)。
等温过程:12ln 21V V nRT dV V nRTPdV WV V ===⎰⎰。
若系统膨胀,W 为正值;若系统压缩,W 为负值。
(三)热力学第二定律:热机在一热力循环过程中,要将能量全部转换为功,这是不可能的,讨论其能量转换的比例,定义热机的效率intotal Q W =ε,故热机的效率无法达到100%。
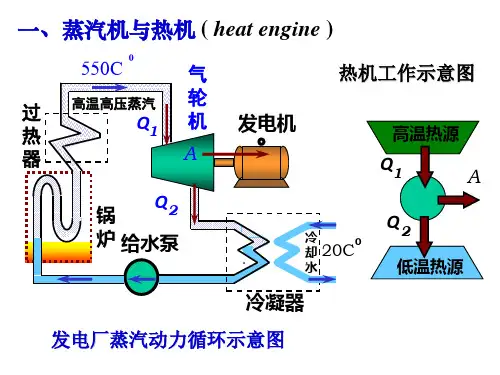

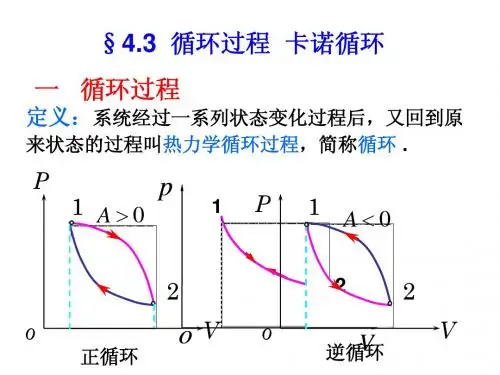

热机知识点总结做功一、热机的基本原理热机的基本原理是利用热量转化为机械能。
根据热机的工作原理可以分为燃烧型热机和非燃烧型热机两大类。
燃烧型热机利用燃料的热能进行燃烧,将产生的热能转化为机械能。
而非燃烧型热机则是利用外部热源直接输入热能,然后进行能量转换。
无论是燃烧型还是非燃烧型热机,其工作原理都遵循热力学的基本原理,即热量流向高温到低温的方向。
热机的基本原理是热机循环过程。
在燃烧型热机中,燃料燃烧产生的高温高压气体推动活塞进行功,将热能转化为机械能。
在非燃烧型热机中,外部热源提供热能使工质膨胀从而推动活塞进行功。
这些都是通过循环过程完成的,即引入工质、吸收热量、做功、放出热量,再重新引入工质的循环过程。
二、热机的工作循环热机的工作循环是指在热机中工质所经历的一系列热力学过程,常见的热机循环有卡诺循环、奥托循环和布雷顿循环等。
这些循环过程为热机的工作提供了理论基础,对于提高热机的效率和性能具有重要意义。
卡诺循环是理想热机的工作循环,它包括等温膨胀、绝热膨胀、等温压缩和绝热压缩四个过程。
在这个过程中,工质依次经历了吸收热量、做功、放出热量和吸收冷量,完成了能量转化的循环过程。
奥托循环是内燃机常见的工作循环,包括吸气、压缩、爆燃、做功和排气五个过程。
在这个过程中,混合气经历了一次爆燃过程,产生了功,推动了活塞,最终完成了一次循环。
布雷顿循环是常见的蒸汽轮机循环,包括等压加热、等熵膨胀、等压冷凝和等熵压缩四个过程。
在这个过程中,水蒸汽依次经历了吸热、膨胀、放热和压缩,完成了能量转化的循环过程。
三、热机的效率热机的效率是衡量热机性能的重要指标。
在热力学中,热机的效率由能量转换率来定义,即功输出与热输入的比值。
在理想热机中,其效率是由卡诺循环效率来决定的,即1-(冷热源温度比)。
实际热机的效率总是小于理想热机的效率,因为在实际过程中总会有能量损失和热量漏散等现象。
因此,提高热机的效率对于能源利用和环境保护具有重要意义。


热机的工作原理热机是一种能够将热能转化为机械能的装置。
它们是现代工业和交通运输领域中不可或缺的设备。
了解热机的工作原理有助于我们更好地理解其在生活中的应用。
本文将介绍热机的基本原理和常见类型。
第一部分:热机的基本原理热机的工作原理基于热力学定律,主要包括热能转化、热传递和工作物质循环三个方面。
1. 热能转化:热机利用热能转化为机械能。
根据热力学第一定律,能量守恒,即输入的热能等于输出的机械能和热能之和。
热机中的工质吸收热量,使其内部分子运动增加,从而产生压力、温度和体积的变化。
2. 热传递:热机通过热传递实现热能输入和输出。
热机中的工质与热源接触后,热能传递给工质,使其温度升高。
通过与冷源接触,工质失去热能,使其温度降低。
这个过程可以通过热交换器来实现,提高能量利用效率。
3. 工作物质循环:热机的工作原理基于工作物质在循环中的状态变化。
常用的热机循环有循环发动机和循环制冷机。
循环发动机包括内燃机和蒸汽机,其工作物质经历压缩、加热、膨胀和冷却四个过程,完成机械能输出。
循环制冷机则通过制冷剂的循环流动,完成热能的转移。
第二部分:热机的应用和分类热机广泛应用于各个领域,包括能源生产、交通运输、制冷空调等。
1. 热机在能源生产中的应用:发电厂利用热机将燃料的热能转化为电能。
核电站使用核能转化为蒸汽能,推动涡轮机转动,从而产生电能。
太阳能发电也是一种利用热机工作原理实现能源转化的方法。
2. 热机在交通运输中的应用:汽车发动机是热机的一种常见应用,通过燃烧混合气体(燃料和空气)释放能量,驱动活塞运动,推动车辆前进。
火车、船舶和飞机等交通工具也广泛使用热机作为能源转换装置。
3. 热机的分类:根据工作原理和工质特性的不同,热机可以分为循环发动机、内燃机、蒸汽机、燃气轮机等。
循环发动机主要用于发电厂和交通工具,内燃机广泛应用于汽车和摩托车,蒸汽机用于蒸汽火车和蒸汽船,燃气轮机一般用于发电厂和大型工业设备。
结论:热机是现代工业和交通运输领域中必不可少的能源转换装置。

斯特林循环和卡诺循环
摘要:
一、斯特林循环与卡诺循环的定义与原理
二、斯特林循环与卡诺循环在能源转换中的应用
三、斯特林循环与卡诺循环的优缺点分析
四、结论
正文:
斯特林循环与卡诺循环是热力学中两种重要的热机循环过程,它们在能源转换领域有着广泛的应用。
斯特林循环是一种理想的热机循环,它的基本原理是通过等温膨胀、绝热膨胀、等温压缩和绝热压缩四个过程完成热力学循环。
在这个过程中,工作物质(如气体)在等温过程中吸收或释放热量,而在绝热过程中则不与外界交换热量。
斯特林循环广泛应用于制冷、气体输送和热力学研究等领域。
卡诺循环是另一种理想的热机循环,它由两个等温过程和两个绝热过程组成。
在卡诺循环中,工作物质在低温热源和高温热源之间进行热交换,从而实现热能的转换。
卡诺循环的热效率与工作物质的性质无关,仅与低温热源和高温热源的温度有关,这使得卡诺循环成为热机效率的理论极限。
斯特林循环和卡诺循环在能源转换领域有着广泛的应用。
斯特林制冷机是一种利用斯特林循环制冷的设备,其具有结构简单、无运动部件、噪音低等优点。
卡诺热机则是一种基于卡诺循环的热机,它具有高热效率、环保等优点,被广泛应用于太阳能发电、汽车发动机等领域。
虽然斯特林循环和卡诺循环在能源转换中具有显著优点,但它们也存在一定的局限性。
斯特林循环的效率相对较低,且在高温应用中需要较大的温差。
卡诺循环则需要较宽的温度范围,这限制了其在实际应用中的发展。
总之,斯特林循环和卡诺循环作为热力学中的两种重要循环过程,在能源转换领域具有广泛的应用前景。
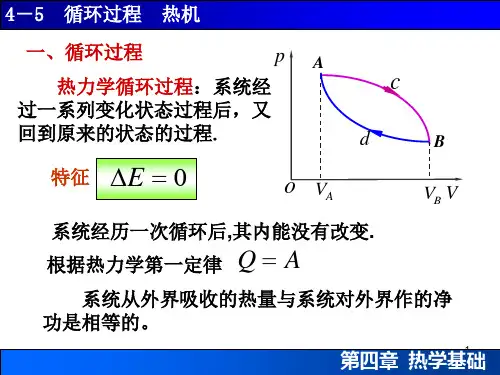
热力学中的循环过程与卡诺热机效率热力学是一门研究热能转换和能量传递规律的学科,而循环过程则是热力学中的一个重要概念。
循环过程是指系统经历一系列状态变化后,最终回到原始状态的过程。
而卡诺热机效率是热力学中用来衡量热机性能的一个重要指标。
热力学循环过程包括两种基本类型:隔热和可逆。
隔热循环过程是指系统与外界没有热交换,只有功交换的过程。
典型的例子是卡诺循环和斯特林循环。
可逆循环过程是指系统中的每一个状态变化都是可逆的,即可逆循环不会产生不可逆损失。
典型的例子是卡诺循环。
卡诺热机是一种理想化的热机,它由两个等温过程和两个绝热过程组成。
卡诺循环是一种最高效的热机,其效率只与工作物质的温度有关,而与具体的工作方式无关。
卡诺热机效率的公式为:η = 1 - Tc/Th其中,η代表卡诺热机的效率,Tc代表冷热源的温度,Th代表热热源的温度。
由该公式可见,卡诺热机的效率随着冷热源温差的增大而增大,同时也随着热热源温度的降低而增大。
卡诺热机效率的理论上限为1,即100%。
然而,在实际应用中,由于存在摩擦、流体阻力等不可避免的不可逆损失,实际工作热机的效率往往低于卡诺热机。
真实热机的效率与卡诺热机效率之间的比值被称为热机的实际效率。
热机的实际效率是衡量热机性能的重要指标之一。
热力学循环过程与卡诺热机效率在能量转换、能量利用以及环境保护方面有着重要的应用价值。
在能源开发和利用中,通过研究热力学循环过程,可以优化能源转换效率,提高能源利用效率。
而卡诺热机效率的研究和应用则可以为热能工程、能源管理等方面提供理论指导和技术参考。
热力学循环过程与卡诺热机效率还与环境保护紧密相关。
随着全球能源需求的增加和环境问题的日益突出,绿色能源的开发和利用成为了全球能源领域的重要课题。
而研究热力学循环过程和提高热机效率,则可以减少能源消耗和排放,降低对环境的影响。
总之,热力学循环过程与卡诺热机效率是热力学中的重要概念和指标。
研究循环过程和提高热机效率对于能源转换、环境保护和能源可持续发展具有重要意义。
热力学循环与热机效率计算热力学循环是指在一定的条件下,系统从初始状态经历一系列的热力学过程最后回到初始状态的过程。
其应用在热机中,通过能量转化来产生动力或执行某种工作。
在研究热力学循环时,我们常常关注的一个重要参数就是热机的效率。
热机效率(η)是指热机输出功(W_out)与吸热热量(Q_in)之比,即:η = W_out / Q_in热机效率是衡量热机性能的一个重要指标,它告诉我们燃料能源转化为有用功的比例。
在热力学循环中,不同类型的循环可以有不同的热机效率计算方法。
接下来,我们将分别介绍开式循环和闭式循环的热机效率计算。
一、开式循环的热机效率计算开式循环是指在工作过程中,工质在一个封闭的系统内部与外部有大量的质量交换。
其中最常见的开式循环是蒸汽汽轮机循环。
1. 卡诺循环效率卡诺循环是理想的热力学循环,它包括两个等温过程和两个绝热过程。
在卡诺循环中,热机效率可以通过热源温度(T_H)和冷库温度(T_C)来计算,即:η = 1 - T_C / T_H其中,T_H表示热源温度,T_C表示冷库温度。
2. 热力学循环效率对于实际的蒸汽汽轮机循环来说,我们可以通过设定一个功率调整系数(υ)来计算热机效率。
热力学循环效率(η_cycle)可以根据下述公式计算:η_cycle = η_Carnot × υ其中,η_Carnot为卡诺循环效率。
二、闭式循环的热机效率计算闭式循环是指工质在工作过程中不与外界发生任何质量交换,最常见的闭式循环是往复式内燃机循环。
1. 高斯定理高斯定理是用来计算往复式内燃机循环的热机效率的公式。
根据高斯定理,热机效率可以通过压缩比(r)和绝热指数(γ)来计算,即:η = 1 - 1 / r^(γ-1)其中,γ表示绝热指数。
2. 奥托循环和迪塞尔循环往复式内燃机循环中,最常见的两种循环是奥托循环和迪塞尔循环。
奥托循环适用于汽油发动机,迪塞尔循环适用于柴油发动机。
奥托循环的热机效率计算公式为:η = 1 - 1 / r^(γ-1)迪塞尔循环的热机效率计算公式为:η = 1 - 1 / r^(γ-1) × (r-1) / γ其中,r表示压缩比,γ表示绝热指数。
循环的热效率公式的两种形式
热力学中的效率,有一个统一的定义,就是“收获比代价”,就比如为了让热机工作,需要让燃料燃烧,释放热量q1,在热机循环过程中,向大气中排放热量q2。
由能量守恒,热机对外做功q1-q2,则在整个循环过程中,q1就是我们付出的代价,q1-q2就是我们的收获,循环效率就是(q1-q2)除以q1。
由于工作物质只能与两个热源交换热量,所以可逆的卡诺循环由两个等温过程和两个绝热过程组成。
热力学第二定律对所有热机的热效率进行了基本的限制。
即使是理想的无摩擦发动机也不能将其100%输入热量的任何地方转换成工作。
热机循环热力发动机(热机)是指各种利用内能做功的机械,其原理是将燃料的化学能转化成内能再转化成机械能的机器动力机械的一类,如蒸汽机、汽轮机、燃气轮机、内燃机、喷气发动机等。
热机通常以气体作为工质(传递能量的媒介物质叫工质),利用气体受热膨胀对外做功。
自热机出现以来,人们一直从实验和理论上研究其效率问题。
大量研究工作一方面为提高热机效率指明了的方向,另一方面推动了热学理论的发展。
【实验目的】(1)研究热机将热转换为功的过程和原理 (2)学会计算热机循环的效率 (3)探索提高热机循环效率的方法【实验原理】热机是依靠从热源吸收热量,向低温热源释放热量来工作一种的装置。
其理论基础为:(一) 理想气体方程式:PV=nRT ,将热力系统视为理想气体,再经热力过程变化时,将满足理想气体方程式。
(二)热力学第一定律:热力过程的变化,由能量守恒的推导,可得:dU = dQ - dW 。
dU 为系统内能变化,dQ 为加入系统的热能,dW 为系统对外界所做的功。
1. 内能函数U 为状态函数,故热力系统经一循环过程,末状态等于初状态,其内能相同,故dU = 0。
2. dQ 为热力过程加入系统的热能,其值和变化的过程有关:绝热过程:dQ = 0。
等压过程:dQ = nC p dT 。
定容过程:dQ = nC v dT 。
其中C p 、C v 分别为气体的定压比热及定容比热。
若系统吸热,dQ 为正值;若排热,dQ 为负值。
3. dW 为热力系统在热力过程中对外界所做的功,其形式为:dW = PdV ,dW 为微量变化的功,在这一完整过程种做功为⎰⎰==PdVdW W ,即热力系统P-V 图曲线下面积。
故: 等压过程:W = P∆V = P(12V V -)。
等温过程:12ln 21V V nRT dV V nRTPdV WV V ===⎰⎰。
若系统膨胀,W 为正值;若系统压缩,W 为负值。
(三)热力学第二定律:热机在一热力循环过程中,要将能量全部转换为功,这是不可能的,讨论其能量转换的比例,定义热机的效率intotal Q W =ε,故热机的效率无法达到100%。
本实验利用两个等压过程,两个等温过程构成一个循环 (如图一) 。
图一其热机循环的过程为:A →B :等温压缩,在固定温度下(室温T L ),使压力由H LP P →。
此等温过程,BAL V V nRT W ln1-=。
B →C :等压膨胀,在固定压力(P H )下,温度由H LT T →,此过程对外作功为)(2B C H V V P W -=,所加热为)(1L H P T T nC Q -=。
C →D :等温膨胀,在固定温度(T H )下,压力由H P 降为L P ,此过程作功为D →A :等压压缩,在固定压力(P L )下,温度由L HT T →,构成一循环过程,其作功为)(4D A L V V P W -=。
其所作总功4321W W W W W+++=)(ln )(lnA D L CD H B C H B A L V V P V VnRT V V P V V nRT --+-+-=加入热量RV V P C T T nC Q Q B C H PL H P in )()(1-=-==1)(11)()(--=--=--=γγγB C H B C H V P B C H P V V P V V P C C V V P C其中VPC C =γ,空气(双原子气体)之40.1=γ故热机效率inQ W =ε1)()(ln )(ln ----+-+-=γγB C H A D L CD H B C H B A L V V P V V P V VnRT V V P V V nRT 。
【实验仪器】热机TD-8572、大支架ME-8735、200g 奥豪斯开槽配重砝码SE-8726、钻孔配重(10g 和20g )648-06508、塑料容器740-183、拉线699-011、旋转运动传感器CI-6538、温度传感器CI-6505B 、压力传感器CI-6534A 。
【实验内容及步骤】在本实验中,热机由一种中空的圆筒构成。
当铝制空罐子侵入热水时,罐子中的空气开始膨胀,膨胀的空气推动活塞,活塞向上举起重物以此做功。
当然,热机循环实验也可以将罐子侵入冷水中,以此来实现气压和圆筒中空气的体积回到实验开始的状态。
(一)计算机的安装1. 将ScienceWorkshop750接口匣电源打开,再开计算机主机。
2. 将温度、压强及滑轮转动感应器接到正确的插口,如图二所示。
3. 启动计算机桌面上DataStudio 软件,在弹出的对话框中选择第二个选项进入“实验设置”页面,点击SW 图标,分别对孔1、2、A 、B 和C 在选项框中选择正确的输入,具体按照图二接口的标注。
图二 Science Workshop750接口闸和窗口接口模拟图图三 热机装置(二)仪器的安装和使用总的实验过程分为四步,(1)B A →:把200g 重物放置于平台上;(2)C B →:把铝制空气罐子从冷水移动到热水中;(3)D C →:把200g 重物从平台上移开;(4)A D →: 把罐子从热水移动到冷水中。
下面详细介绍整个实验过程。
1. 各准备大约20℃冷水及80℃热水,约至容器的四分之三。
2. 将活塞调至刻度20ml 左右,再将右边的插孔接上压力感应器。
3. 活塞仪左边的插孔接上铝制罐子,并将其放入20℃的冷水中,此时温度感应器也一并放在冷水中,同时按下电脑上的“启动”键,迅速把200g 砝码放在活塞仪上。
4. 等到活塞不再移动后,迅速将铝制空气室移至80℃的热水中。
5. 待活塞停止上升后,移走其上所有的砝码。
6. 再次等待活塞停止上升,再迅速将铝制空气室移至22℃的冷水中。
7. 直到活塞不再下降,按下电脑上的“停止”键,实验结束,至左下角“显示”窗口中读取所得的数据。
“显示”中选择“图表”,选择“压力通道”,出现压力(纵轴)和时间(横轴)的关系图,左键点击横轴的时间,选择体积“V=pi*r*r*x*100”,这时出现P-V 图。
8. 绘出的P-V 图,显示出整个循环过程。
计算循环路径所包围的面积(即热机循环对外所作的功),并和理论值比较。
9.计算出本热机的效率,并与理想热机效率HLT T -=1ε比较。
(三)实验结束后进行以下操作:1. 将循环图表打印出来。
在图表的四个角上面标明A,B,C 和D 。
确定A,B,C,D 点的温度。
在图表上标注箭头以此显示出循环过程的方向。
2. 确定A-B,B-C,C-D,D-A 这四个过程属于哪种类型(例如:等温),确定这些过程中有哪些物理过程(例如:放上重物,放入热水中)。
3. 确定并且标注哪两个过程中气体热能增加。
4. 在B-C 过程中气体等温膨胀,气体从热源吸热,计算此过程中气体热量增加Q H ,然后计算以下参数:a)我们不知道初始体积V ,但我们可以根据测量罐子的体积和圆筒里面初始空气的体积从而计算出V ,当然塑料管中的体积是被忽略的。
cylinder o can Ah h r V )()(2+=π这里A 是活塞的横截面积。
用等压条件下理想气体定律D DA A T V T V =来计算V D 。
b) 用等温条件下理想气体定律计算V C :P C V C =P D V D 。
c)计算Q C →D 。
在等温条件下,Q = nRT ln(V f /V i ),因为PV = nRT, 所以Q C→D = P D V D ln (V D /V C ),绝对压强P=P 仪表 + P 大气。
d) 计算Q B →C ,在等压条件下,Q = nCp ∆T ,并且因为空气为二原子分子气体,Cp = 5/2 R, nR =PV/T ,)(27D C DDD CB T T T V P Q -=→。
e) 计算Q H = Q B →C + Q C →D 。
5.根据测量到曲线内的面积来计算气体所做的功。
6. 计算效率%100x Q We H=。
【注意事项】(1)配重砝码为200g ,禁止超重。
(2)旋转运动传感器、温度传感器和低压传感器均为精密电子仪器,禁止对其碰撞。
(3)铝制空罐子在冷热水中转换时,动作要迅速,以免外界对其影响,引入实验误差。
【思考题】(1)经过热机做功A→B→C→D→A循环后,理论上会回到A点,但实验的结果并没有回到A点,试着讨论其原因并提出改善的方法。
(2)热机在循环过程中,如果其效率e=1,并不违反热力学第一定律,但为什么实际做不到?(3)若B-C的循环步骤温度差异愈大,将对整个实验有何影响?试讨论之。
(4)如何提高热机的效率?。